查找算法
一.前言
查找是在大量的信息中寻找一个特定的信息元素,在计算机应用中,查找是常用的基本运算, 是很多程序中最耗时间的一部分,查找方法的优劣对系统运行效率影响很大。
我会带大家一起学习几种常见的查找算法
1.顺序查找 2.二分查找 3.插值查找 4.斐波那契查找 5.分块查找 6.树表查找 7.散列表查找 *
二.基本概念
1.查找:是指在数据元素集合中查找满足某种的数据元素的过程,例如:在学生成绩表中查找某一学生的成绩、在字典查找某个字等。
2.查找表:用于查找的数据元素集合称为查找表,查找表由同一类型的数据元素组成。
3.关键字:数据表中数据元素一般有多个属性域,其中有一个属性域可用来区分元素,作为查找或排序的依据,该域即为关键字。
主关键字:能唯一标识数据元素的关键字,例如,成绩表中学生的学号,是唯一的。
次关键字:不能唯一标识数据元素的关键字,例如,学生的姓名,因为可能出现两个名字相同的学生的情况。
4.动态查找和静态查找
若在查找的同时对表做修改运算(如插入和删除),则称这类查找为动态查找,否则为静态查找。静态查找。
在查找过程中查找表本身不发生变化,而动态查找表则有可能发生变化。相比较而言,静态查找表的结构较 为简单,操作较为方便,但查找的效率较低,而且需要考虑表的溢出问题。
5.内查找和外查找
若整个查找的过程全部在内存中进行,则称其为内查找;若在查找过程中还需要访问外存,则称其为外查找。
6.平均查找长度(ASL)
查找的时间复杂度一般用平均查找长度(ASL)来衡量。平均查找长度是指在数据表中查找各数据元素所需 进行的关键字比较次数的期望值。
三.分类
1.顺序查找
顺序查找又称线性查找(Sequential Search),是一种最简单、最基本的静态查找方法。其基本思想是:从表的一端开始,扫描整个线性表,依次将扫描的结点关键字与给定值K进行比较,若当前扫描的关键字结点与K相等,则查找成功;若扫描结束后,仍未找到关键字值等于K的结点,则查找失败。
顺序查找所用的时间跟查找关键字K在表中的位置有关。若在长度为n的查找表中超找K值,最好的情况是K在查找表的第一个位置,这样只需要一次查找就能查找成功;最坏的情况是K在查找表最后一个位置或者K根本不在查找表中,此时需要遍历整个查找表。顺序表查找的时间复杂度为O(n)。
顺序查找的优点是算法简单,且对表的结构没有任何要求,无论是用顺序表还是用链表存放记录,也无论记录之间是否按关键字有序存放,都适用顺序查找。顺序查找的确定是超找效率低,因为在较大规模的数据集合中进行查找时,不宜采用顺序查找。
2.二分查找
二分查找又称折半查找(Binary Search),是一种效率比较高的静态查找方法。二分查找要求各数据元素按关键字有序(升序或降序)排列,并且要求查找表使用线性表的顺序存储结构。也就是说,二分查找只适用于对有序的顺序表进行查找。
假设在一个有n个元素的查找表中查找K值,二分查找的思想是,首先将K值与查找表中中间位置上的元素进行比较,若相等,则查找成功;否则,中间元素将查找表分成两个部分,前一部分中的元素均小于中间元素,而后一部分元素均大于中间元素。因此,K于中间元素比较以后,若K值小于中间元素,则应在前一部分查找,否则在后一部分查找。重复上述过程,直至查找成功或失败。
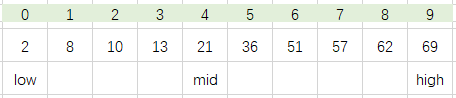
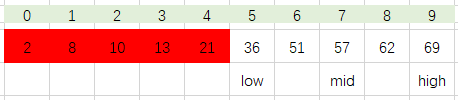
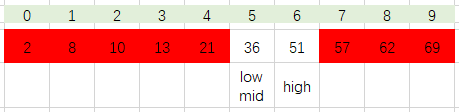
如图演示有10个元素的有序查找表(2,8,10,13,21,36,51,57,62,69)中查找关键字为51的数据元素:
二分查找可用一颗称为判定树的二叉树来描述,判定树中每一个结点对应表中一个元素,但结点的值不是关键字的值,而是元素在表中的位置。根结点对应当前区间的中间元素,左子树对应左子表,右子树对应右子表。
显然二分查找成功时,与关键字比较的次数最多不超过判定树的深度。
而具有n个节点的判定树的深度和n个结点的完全二叉树的深度相等。均为logn+1 二分查找的时间复杂度为O(logn),也就是说在10000条记录的有序查找表中, 平均只需要找14次就可找到指定元素。
二分查找的优点是比较次数少,查找速度快,效率非常高。但是由于查找之前需要 将表按照关键字排序,排序本身就是一种很费时的运算,因此二分查找适用于不经常 变动而查找频繁的有序表。
在C#中,System.Collection.SortedList
Add() 添加元素
Remove()删除元素
Count 元素的个数
Capacity 容量
This[] 索引器
3.插值查找
插值查找是二分查找上的一个优化。
mid=(low+high)/2, 即mid=low+1/2*(high-low);
通过类比,我们可以将查找的点改进为如下:
mid=low+(key-a[low])/(a[high]-a[low])*(high-low),也就是将上述的比例参数1/2改进为自适应的,根据关键字在整个有序表中所处的位置,让mid值的变化更靠近关键字key,这样也就间接地减少了比较次数。
基本思想:基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率。当然,差值查找也属于有序查找。
注:对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好的多。反之,数组中如果分布非常不均匀,那么插值查找未必是很合适的选择。
复杂度分析:查找成功或者失败的时间复杂度均为O(log2(log2n))。
4.斐波那契查找
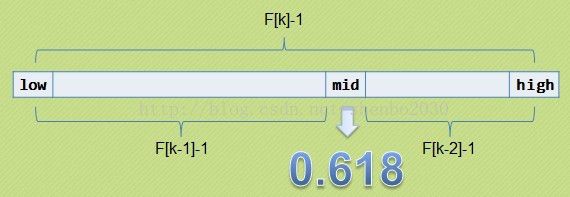
斐波那契查找是二分查找的一种提升算法,通过运用黄金比例的概念在数列中选择查找点进行查找。
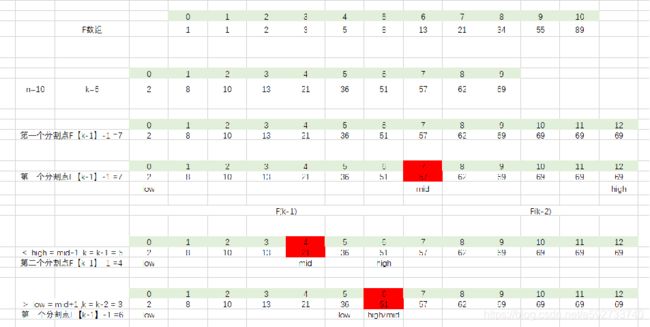
相对于二分查找和差值查找,斐波那契查找的实现略显复杂。但是在明白它的主体思想之后,掌握起来也并不太难。 他要求开始表中记录的个数为某个斐波那契数小1,即n=F(k)-1
概念:
黄金比例,又称黄金分割,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分 之比等于整体与较大部分之比,其比值约为1:0.618或0.618:1。
0.618被公认为最具有审美意义的比例数字,这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、 建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。
斐波那契数列,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89……. 从第三个数开始,后边每一个数都是前两个数的和,然后我们会发现,随着斐波那契数列的递增,前后两个数的比值会越来越接近0.618,利用这个特性,我们就可以将黄金比例运用到查找技术中。
5.分块查找
分块查找又称索引查找,是针对分块有序数据的一种静态查找算法。
分块有序是把数据集的记录分成若干块,并且这些块满足两个条件:
1.块内无序:不一块内的记录不需要有序,当然你如果能让块内有序,对查找来说更理想,不过这要付出大 量的时间和空间代价,通常我们不要求块内有序。
2.块间有序:例如,要求第二块内记录关键字都必须大于第一块内记录的关键字,第三块记录的关键字均大 于第二块记录的关键字,……,因为只有块间有序,才有可能给查找带来效率。
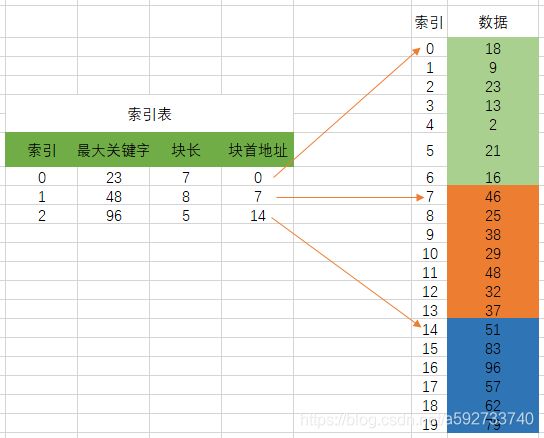
分块索引表一般分为三个数据项:
1.最大关键字:它存储每一块中的最大关键字,这样的好处就是 可以使得在他之后的下一块中的最小关键字也能比 这一块最大的关键字要大。
2.块长:储存块中记录的个数,以便于循环时使用。
3.首块地址:指向首块数据元素的指针,便于开始对这一块记录遍历。
例如,我们需要查数据32,首先查找索引表,由于23<32<48,因此确定32 在索引7-13处,因此只需要在7-13所在的位置进行查找即可得到结果。 由于索引表有序,因为可以采用二分查找方法快速确定元素所在块. 由于数据块内元素无序,因此只能采用简单低效的顺序查找方式进行。
分块查找的时间复杂度为O(n^0.5),他的效率介于顺序查找和二分查找之间,是顺序查找和二分查找的一个折中方案。
在分块查找中,不同的数据类型有不同的划分方法,把一个顺序表划分为多少块及每块的大小都要根据实际情况来确定。不具有通用性,所以我们只介绍下理论。
6.二叉查找树
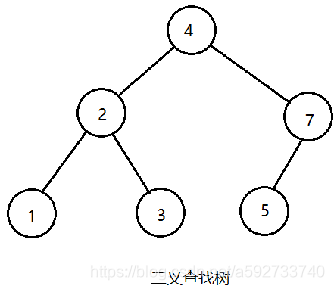
二叉查找树(Binary Search Tree,BST)又称为二叉排序树(Binary Sort Tree),他是满足如下性质的二叉树:
1.若他的左子树非空,则左子树上所有的记录均小于根记录的值。
2.若他的右子树非空,则右子树上所有的记录均大于根记录的值。
3.左、右子树本身又各是一棵二叉查找树。
二叉查找树是递归定义的,其一般理解是:二叉树中的任意一点,其值为k,只要该节点有左孩子,则左孩子的值必小于k,只要有右孩子,则右孩子的值必大于k,二叉查找树的一个重要性质是:中序遍历该树得到的序列是一个递增有序序列。
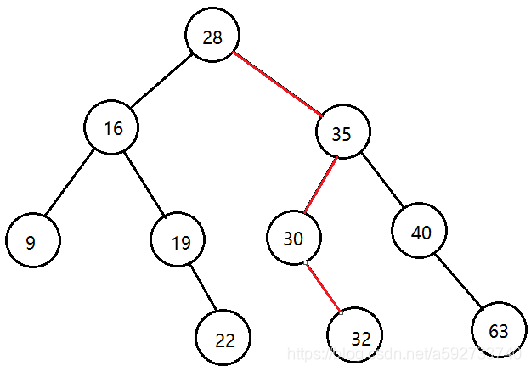
如图所示查找32结点的示意图:
二叉查找树和二分查找的判定树很相似。
判定树,由于二分查找表是有序的,所以无论按照什么样的顺序 插入,二分查找的判定树只有一个;但是二叉查找树中,如果元素 的插入顺序不同,他生成的二叉查找树有可能不同。
6.1 BST-插入
已知一个关键字为k的节点,若将其插入到二叉查找树中,只要保证插入后仍符合二叉查找树的定义即可。新插入的结点一定是一个新添加的叶子节点,结点的插入方法如下:
1.若二叉树是空树,则k成为二叉查找树的根。
2.若二叉查找树非空,则将k与二叉查找树的根进行比较,如果k = 根的值,停止插入;k < 根的值,则将k插 入到左子树;k > 根的值,则将k插入到右子树。
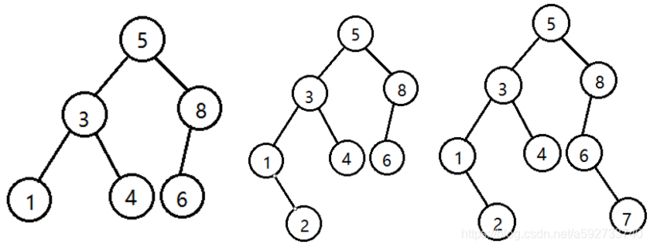
如图演示关键字序列为(5,8,3,4,6,1,2,7)插入的过程:
6.2 BST-删除
二叉查找树的删除比较麻烦,在删除结点的时,不能把以该结点为根的子树都删掉,只能删除该结点,并且还保证删除后所得的二叉树仍满足二叉查找树的性质。
假如要删除结点p,结点p的双亲为f,我们分三种情况讨论:
1.p为叶子结点,直接删除
2.p只有一个孩子,删除后,让孩子取代p
3.p有两个孩子,右子树的最小值替换他或者左子树的最大值替换他,然后删除自己
6.3 BST-优化
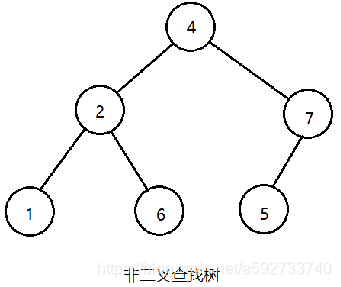
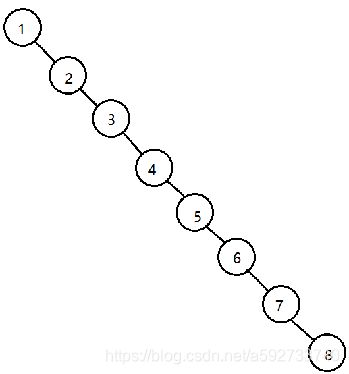
若同样的集合,插入顺序改为(1,2,3,4,5,6,7,8),那么上述算法生成的二叉树就如图所示:
可以看到,不同的插入顺序将得到不同的二叉查找树,最糟糕的情况是插入一个有序序列, 使得具有n个元素的集合生成高度为n的单支二叉树,从而导致他的查找性能接近线性表。
前苏联科学家G.M.Adelson-Velskii和E.M.Landis提出了自平衡二叉查找树。 这种二叉树在插入和删除操作中,可以通过一系列的旋转操作来保持平衡。 从而保证了二叉查找树的效率,最终这种二叉树以他们的名字命名AVL-Tree, 他也被称为平衡二叉树。
另一种与AVL树相似的树是红黑树,也被称为平衡二叉B树。他跟AVL-Tree原理非常 接近,区别在于他使用颜色来标识结点的高度,并且它追求的是局部平衡,而AVL是非常严格 的平衡
6.4 AVL树的平衡
AVL树的每一个结点都有一个平衡因子(Balance Factor,BF),它表示这个结点的左、右子树的高度差。
AVL树上所有的结点的BF值只能是-1,0,1,反之就不是平衡二叉树。