论文阅读《Centralized Feature Pyramid for Object Detection》

论文地址：https://arxiv.org/pdf/2210.02093.pdf
源码地址：https://github.com/QY1994-0919/CFPNet

---

概述

   特征金字塔模块在众多计算机视觉任务中都有优异的性能表现。针对现有的方法过渡关注于层间的特征交互而忽略了层内的特征交互的问题，本文提出一种基于全局显式集中式特征调节的中心化的特征金字塔（Centralized Feature Pyramid, CFP） 用于目标检测任务。其中，发明了一个空间视觉中心策略用于捕获信息，包含一个捕获全局长程依赖的轻量化MLP与一个捕获局部角落区域信息的可学习的视觉中心机制；提出了一种用于自上而下特征金字塔的全局集中式调节方法，使用最深层内层特征获得的显示视觉中心信息来调节前端浅层特征。与现有的特征金字塔相比，CFP具有长程特征依赖关系捕获能力，而且能获得有效的特征表示。在MS-COCO上的实验结果验证了所提出的CFP可以在最先进的YOLOv5和YOLOX对象检测基线上实现一致性性能增益。文章的主要贡献如下：

• 提出一种空间显示视觉中心方案，包括用于捕获长程依赖关系的轻量级MLP与用于聚合关键局部区域的可学习视觉中心机制。
• 提出一种用于特征金字塔结构的全局集中式调节方法。
• CFP在目标检测 Baseline 上获得一致的性能提升。

---

模型架构

Centralized Feature Pyramid (CFP)

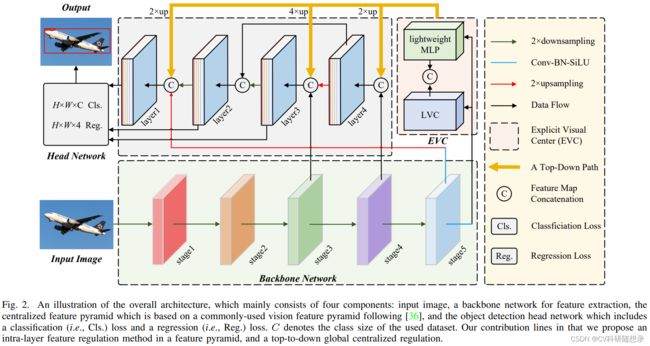
  现有的方法主要聚焦于层间特征的交互而忽略了层内特征调节对识别任务的作用，受到密集预测任务的启发，本文提出一种用于目标检测的集中式特征金字塔（CFP），该方法基于全局显示中心化层间特征调节。与现有的特征金字塔相比，前者不仅能捕获全局特征的长程依赖关系，也能提取到差异化的特征表达。如图2所示，CFP包含以下几个部分：输入图像、基于CNN的骨干网络与提取到的特征金字塔、Explicit Visual Center（EVC）、Global Centralized Regulation(GCR)、用于目标检测的检测头（分类孙素、回归损失分割损失）。ECV与GCR都是在特征金字塔上实现的。
   给定输入图像，使用骨干网络提取输入图像的5个尺度下的特征，构建5层的特征金字塔$\mathbf{X}，其中每一层的特征为 ${\mathbf{X}}_i(i=0,1,2,3,4)$ 分别对应 $1/2,1/4,1/8,1/16,1/32$ 的尺度。继而使用基于轻量级的MLP的来捕获特征${\mathbf{X}}_4$的长程依赖关系，并使用可学习的视觉中心机制来聚合输入图像的局部角区域。 此外，使用GCR来将深层特征的视觉中心信息来调节浅层特征（即${\mathbf{X}}_3$ 到 ${\mathbf{X}}_2$），最后将这些特征聚合到解耦头网络中进行分类和回归计算。

Explicit Visual Center (EVC)

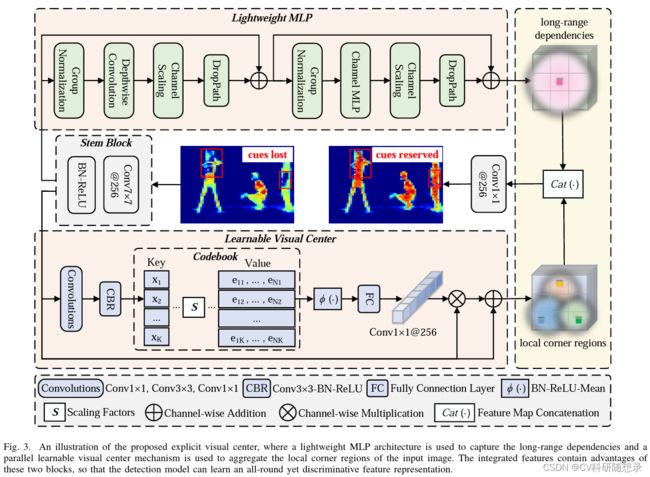
  显示视觉中心包含两个部分：轻量级MLP层与可学习的视觉中心机制。其中轻量级MLP用于处理${\mathbf{X}}_4$ 来捕获特征的长程依赖关系，可学习的视觉中心机制用于捕获局部信息特征，最后将两个特征沿着特征维度进行拼接作为EVC的输出。在实现过程中，使用一个$7\times 7$且输出通道为256的卷积伴随着BN与激活层的block来对 ${\mathbf{X}}_4$ 进行滤波，然后送入EVC中，如式1所示：
$$\mathbf{X}=\mathrm{cat}\left(\mathrm{MLP}\left({\mathbf{X}}_{\text{in }}\right);\mathrm{LVC}\left({\mathbf{X}}_{\text{in }}\right)\right)\text{\hspace{1em}(1)}$$
其中$\mathbf{X}$ 是EVC的输出，cat为沿着特征维度的拼接。${\mathbf{X}}_{in}$是Stem block的输出，如式2所示：
$${\mathbf{X}}_{\text{in }}=\sigma \left(\mathrm{BN}\left({\mathrm{Conv}}_{7\times 7}\left({\mathbf{X}}_4\right)\right)\right)\text{\hspace{1em}(2)}$$

轻量化的MLP主要由两个残差块组成：深度可分离卷积模块，沿着通道的MLP模块。两个块都伴随着通道随访和DropPath操作来提高特征的泛化与鲁棒性。深度可分离卷积模块的输入是经过组归一化的特征图 ${\mathbf{X}}_{in}$，深度可分离卷积可以在较低的计算成本下提高特征的表达能力：
$${\tilde{\mathbf{X}}}_{\text{in }}=\mathrm{DConv}\left(\mathrm{GN}\left({\mathbf{X}}_{\text{in }}\right)\right)+{\mathbf{X}}_{\text{in }}\text{\hspace{1em}(3)}$$
MLP模块的输入为深度可分离卷积模块的输出，且经过组归一化后再沿着通道进行MLP操作：
$$\mathrm{MLP}\left({\mathbf{X}}_{\text{in }}\right)=\mathrm{CMLP}\left(\mathrm{GN}\left({\tilde{\mathbf{X}}}_{\text{in }}\right)\right)+{\tilde{\mathbf{X}}}_{\text{in }}\text{\hspace{1em}(4)}$$

LVC为一个具有内在字典的编码器，主要由两个部分组成：（1）固定码本： $\mathbf{B}=\{{\mathbf{b}}_1,{\mathbf{b}}_2,...,{\mathbf{b}}_K,\}$，其中 $N=H\times W$ 为输入特征图的尺寸。（2）可学习的视觉中心缩放因子 $\mathbf{S}=\{s_1,s_2,...,s_K\}$。来自Stem的特征$X_{in}$ 经过一组卷积层（包括1×1卷积、3×3卷积和1×1卷积）的 block 进行编码。将编码后的特征被处理为 CBR 块，该块由带有BN层和ReLU激活函数的3×3卷积组成。将编码后的特征${\check{\mathbf{X}}}_{in}$进入码本。最后使用一组缩放因子 $s$ 来依次使 ${\check{x}}_i$ 和 $b_k$ 映射相应的位置信息。整图的第 $k$ 个码字信息计算如式5所示：
$${\mathbf{e}}_k=\sum _{i=1}^N\frac{e^{-{\mathbf{s}}_k{\Vert {\check{\mathbf{x}}}_i-{\mathbf{b}}_k\Vert }^2}}{{\sum }_{j=1}^K{e}^{-{\mathbf{s}}_k{\Vert {\check{\mathbf{x}}}_i-{\mathbf{b}}_k\Vert }^2}}\left({\check{\mathbf{x}}}_i-{\mathbf{b}}_k\right)\text{\hspace{1em}(5)}$$
其中${\check{\mathbf{x}}}_i$ 为第 $i$ 个像素点， $b_k$ 为第 $k$ 个可学习视觉码字，$s_k$ 为对应的缩放因子。 ${\check{\mathbf{x}}}_i-{\mathbf{b}}_k$ 为每个位置的像素位置相对于码字的信息，$K$ 是视觉中心的数量。最后使用 $\varphi$ 来融合所有的 $e_k$，其中 $\varphi$ 包含一个BN、ReLU激活与取均值层。
$$\mathbf{e}=\sum _{k=1}^K\varphi \left({\mathbf{e}}_k\right).\text{\hspace{1em}(6)}$$
获得了输出的码字后，使用 $1\times 1$ 的卷积层来预测突出关键类别的特征，最后将输入特征 ${\mathbf{X}}_{in}$ 与经过$1\times 1$ 卷积与激活后的缩放系数 $\delta$沿着通道维度相乘，如式7所示：
$$\mathbf{Z}={\mathbf{X}}_{\text{in }}\otimes \left(\delta \left({\mathrm{Conv}}_{1\times 1}(\mathbf{e})\right)\right)\text{\hspace{1em}(7)}$$
最后基于残差学习的思想，得到LVC学习后的特征：
$$\mathrm{LVC}({\mathbf{X}}_{in})={\mathbf{X}}_{in}\oplus \mathbf{Z}\text{\hspace{1em}(8)}$$
其中 $\oplus$ 为沿着通道维度的相加。

Global Centralized Regulation (GCR)

  EVC是一种层内特征调节方法，该方法不仅能提取全局长程依赖关系，且能尽可能地保留输入图像的局部角落区域信息，这对密集预测任务非常重要。然而，在特征金字塔的每个层次上使用EVC都会导致巨大的计算开销。为了提高内层特征调节的计算效率，文中使用一种自顶向下的特征金字塔GCR，用于在整个特征金字塔上实现跨层特征规范化。为了提高计算效率，首先在最深层 $X_4$ 上实现空间显示视觉中心（ECV），继而使用包含空间视觉中心的特征 $X$ 上采样到不同尺度用于调整所有层的特征。在实现过程中，将深层特征上采样到与低层特征相同的空间尺度，然后沿着特征维度进行拼接后通过 $1\times 1$ 的卷积block降采样到256维度。以此来自顶向下路径中显式增加每一层特征金字塔中全局表示的空间权重，从而使CFP能够有效地实现全面而有区别的特征表示。

---

实验结果