Java 大文件排序
大文件排序
http://en.wikipedia.org/wiki/Merge_sort
http://en.wikipedia.org/wiki/External_sorting
外排序
通常来说,外排序处理的数据不能一次装入内存,只能放在读写较慢的外存储器(通常是硬盘)上。
外排序通常采用的是一种“排序-归并”的策略。
在排序阶段,先读入能放在内存中的数据量,将其排序输出到一个临时文件,依此进行,将待排序数据组织为多个有序的临时文件。之后在归并阶段将这些临时文件组合为一个大的有序文件,也即排序结果。
外排序的一个例子是外归并排序(External merge sort),它读入一些能放在内存内的数据量,在内存中排序后输出为一个顺串(即是内部数据有序的临时文件),处理完所有的数据后再进行归并。
[1][2]比如,要对900 MB的数据进行排序,但机器上只有100 MB的可用内存时,外归并排序按如下方法操作:
读入100 MB的数据至内存中,用某种常规方式(如快速排序、堆排序、归并排序等方法)在内存中完成排序。
将排序完成的数据写入磁盘。
重复步骤1和2直到所有的数据都存入了不同的100 MB的块(临时文件)中。在这个例子中,有900 MB数据,单个临时文件大小为100 MB,所以会产生9个临时文件。
读入每个临时文件(顺串)的前10 MB( = 100 MB / (9块 + 1))的数据放入内存中的输入缓冲区,最后的10 MB作为输出缓冲区。(实践中,将输入缓冲适当调小,而适当增大输出缓冲区能获得更好的效果。)
执行九路归并算法,将结果输出到输出缓冲区。一旦输出缓冲区满,将缓冲区中的数据写出至目标文件,清空缓冲区。一旦9个输入缓冲区中的一个变空,就从这个缓冲区关联的文件,读入下一个10M数据,除非这个文件已读完。
这是“外归并排序”能在主存外完成排序的关键步骤 – 因为“归并算法”(merge algorithm)对每一个大块只是顺序地做一轮访问(进行归并),每个大块不用完全载入主存。
为了增加每一个有序的临时文件的长度,可以采用置换选择排序(Replacement selection sorting)。
它可以产生大于内存大小的顺串。具体方法是在内存中使用一个最小堆进行排序,设该最小堆的大小为 {displaystyle M} M。
算法描述如下:
-
初始时将输入文件读入内存,建立最小堆。
-
将堆顶元素输出至输出缓冲区。然后读入下一个记录:
-
若该元素的关键码值不小于刚输出的关键码值,将其作为堆顶元素并调整堆,使之满足堆的性质;
-
否则将新元素放入堆底位置,将堆的大小减1。
-
重复第2步,直至堆大小变为0。
此时一个顺串已经产生。将堆中的所有元素建堆,开始生成下一个顺串。[3]
此方法能生成平均长度为 {displaystyle 2M} 2M的顺串,可以进一步减少访问外部存储器的次数,节约时间,提高算法效率。
归并的方法
二路归并
各片段均已采用内排序算法进行排序,每次读入2路有序片段的前m个元素进行归并;若输出缓冲区已满,则将已归并好的元素写入文件;
若其中一路m个元素归并完成,读入该路剩下的前m个元素。重复交替执行,直到所有元素都归并完成为止
缺点:元素需要反复比较,比较次数过多,导致归并的效率很低。
k路归并
基于二路归并多次比较的缺点,有人提出了改进算法,采用多路归并来提高效率。
k路归并可以使用堆进行排序,利用完全二叉树的性质,可以很快更新,保持堆的性质。
但是,操作次数不够精简。
胜者树
归并过程:
1、在拆分成k个文件并排序后,取每个文件的首个元素作为叶子节点,构建一颗胜者树
2、输出一个最值到缓冲区;如果缓冲区已满,则将数据写入文件
3、从输出的值对应的来源文件取元素,加入到胜者树中,同时调整树
4、重复第2、3步骤,直到所有数据都读取并归并,最终得到排序的文件
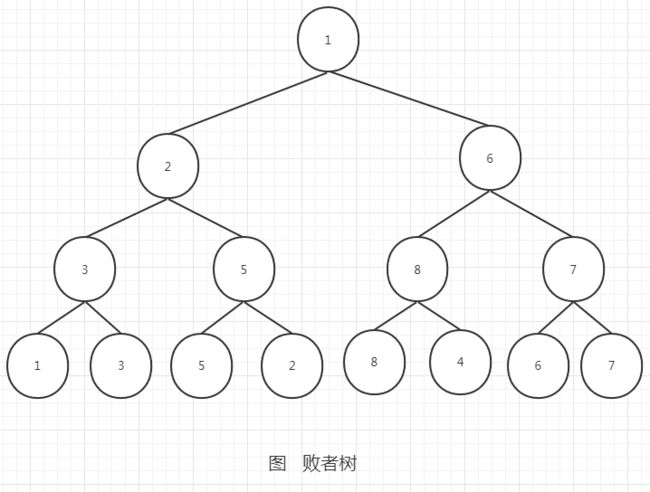
败者树
归并过程:
1、在拆分成k个文件并排序后,取每个文件的首个元素作为叶子节点,构建一颗败者树
2、输出一个最值到缓冲区;如果缓冲区已满,则将数据写入文件
3、从输出的值对应的来源文件取元素,加入到胜者树中,同时调整树
4、重复第2、3步骤,直到所有数据都读取并归并,最终得到排序的文件
败者树将败者存放在父结点中,而胜者再与上一级的父结点比较。败者树的更新只需将子节点与父节点比较。
总结
1、大文件过大,不能一次加载,所以需要拆分成k个小文件
2、k个小文件各自排序,为下一步文件归并打好铺垫
3、二路归并元素比较次数过多,效率低
4、k路归并中,堆排序可以很快更新,但操作数不够精简;胜者树父节点记录胜利的一方,更新时需要比较父节点和兄弟节点;败者树是胜者树的一种变体,父节点记录失败的一方,同时胜利一方与上一级的父节点比较,更新只需要比较父节点。因此在实际应用中采用败者树更好。
linux shell 实现
一种简单解决方案就是分而治之,先打大文件分词大小均匀的若干个小文件,然后对小文件排好序,最后再Merge所有的小文件,在Merge的过程中去掉重复的内容。
在Linux下实现这个逻辑甚至不用自己写代码,只要用shell内置的一些命令: split, sort就足够了。
我们把这个流程用脚本串起来,写到shell脚本文件里。文件名叫 sort_uniq.sh.
- sort_uniq.sh
[sh]
#!/bin/bash
lines=$(wc -l $1 | sed 's/ .*//g')
lines_per_file=`expr $lines / 20`
split -d -l $lines_per_file $1 __part_$1
for file in __part_*
do
{
sort $file > sort_$file
} &
done
wait
sort -smu sort_* > $2
rm -f __part_*
rm -f sort_*
使用方法:./sort_uniq.sh file_to_be_sort file_sorted
这段代码把大文件分词20或21个小文件,后台并行排序各个小文件,最后合并结果并去重。
如果只要去重,不需要排序,还有另外一种思路:对文件的每一行计算hash值,按照hash值把该行内容放到某个小文件中,假设需要分词100个小文件,则可以按照(hash % 100)来分发文件内容,然后在小文件中实现去重就可以了。
外部排序
外部排序指的是大文件排序,即待排序的记录存储在外存储器上,待排序的文件无法一次装入内存,需要在内存和外部存储器之间进行多次数据交换,以达到排序整个文件的目的。
一般来说外排序分为两个步骤:预处理和合并排序。
首先,根据可用内存的大小,将外存上含有n个纪录的文件分成若干长度为t的子文件(或段);
其次,利用内部排序的方法,对每个子文件的t个纪录进行内部排序。这些经过排序的子文件(段)通常称为顺串(run),顺串生成后即将其写入外存。
这样在外存上就得到了m个顺串(m=[n/t])。
最后,对这些顺串进行归并,使顺串的长度逐渐增大,直到所有的待排序的记录成为一个顺串为止。
初始顺串
预处理阶段最重要的事情就是选择初始顺串。通常使用的方法为置换选择排序,它是堆排序的一种变形,实现思路同STL的partial_sort。步骤如下:
(1)初始化堆
从磁盘读入M个记录放到数组RAM中;
设置堆末尾标准LAST=M-1;
建立最小值堆。
(2)重复以下步骤直到堆为空
把具有最小关键码值的记录Min也就是根节点送到输出缓冲区;
设R是输入缓冲区中的下一条记录,如果R的关键码大于刚刚输出的关键码值Min,则把R放到根节点,否则使用数组中LAST位置的记录代替根节点,并将刚才的R放入到LAST所在位置,LAST=LAST-1;
(3)重新排列堆,筛出根节点。
如果堆的大小是M,一个顺串的最小长度就是M个记录,因为至少原来在堆中的那些记录将成为顺串的一部分,如果输入时逆序的,那么顺串的长度只能是M,最好情况输入是正序的,有可能一次性就能把整个文件生成一个顺串,由此可见生成顺串的长度是大小不一的,但是每个顺串却是有序的,利用扫雪机模型能够得到平均顺串的长度为2M。
外部排序最常用的算法是多路归并排序,即将原文件分解成多个能够一次性装入内存的部分,分别把每一部分调入内存完成排序。
然后,对已经排序的子文件进行归并排序。
合并排序
(1) 二路合并排序
二路合并是最简单的合并方法,合并的实现与内排序中的二路归并算法并无本质区别,下面通过具体例子,分析二路合并外部排序的过程。
有一个含有9000个纪录的文件需要排序(基于关键字)。
假定系统仅能提供容纳1800个纪录的内存。文件在外存(如磁盘)上分块存储,每块600个纪录。
外部排序的过程分为生成初始顺串和对顺串进行归并排序两个阶段。在生成初始顺串阶段,每次读入1800个纪录(即3段)待内存,采用内排序依次生成顺串依次写入外存储器中。
顺串生成后,就开一开始对顺串进行归并。首先将内存等分成3个缓冲区,每个缓冲区可容纳600个纪录,其中两个为输入缓冲区,一个为输出缓冲区,每次从外存读入待归并的块到输入缓冲取,进行内部归并,归并后的结果送入输出缓冲区,输出缓冲区的记录写满时再将其写入外存。若输入缓冲区中的纪录为空,则将待归并顺串中的后续块读入输入缓冲区中进行归并,直到待归并的两个顺串都已归并为止。重复上述的归并方法,由含有5块(每块上限1800个记录)的顺串经二路归并的一遍归并后生成含有3块(每块上限3600个记录)的顺串,再经过第二遍……第s遍(s=[],m为初始顺串的个数),生成含有所有记录的顺串,从而完成了二路归并外部排序。
对文件进行外部排序的过程中,因为对外存的读写操作所用的操作的时间远远超过在内存中产生顺串和合并所需的时间,所以常用对外存的读写操作所用的时间作为外部排序的主要时间开销。
分析一下上述二路归并排序的对外存的读写时间。
初始时生成5个顺串的读写次数为30次(每块的读写次数为2次)。
类似地,可得到二路、三路……多路合并方法。
(2) 多路替代选择合并排序
采用多路合并技术,可以减少合并遍数,从而减少块读写次数,加快排序速度。
但路数的多少依赖于内存容量的限制。此外,多路合并排序的快慢还依赖于内部归并算法的快慢。
设文件有n个纪录,m个初始顺串,采用k路合并方法,那么合并阶段将进行遍合并。k路合并的基本操作是从k个顺换的第一个纪录中选出最小纪录(即关键字最小的纪录),把它从输入缓冲区移入输出缓冲区。若采用直接选择方式选择最小元,需要k-1次比较,遍合并共需n(k-1)=次比较。
由于随k的增长而增长,则内部归并时间亦随k的增大而增大,这将抵消由于增大k而减少外存信息读写时间所得的效果。
若在k个纪录中采用树形选择方式选择最小元,则选择输出一个最小元之后,只需从某叶到根的路径上重新调整选择树,即可选择下一个最小元。
重新构造选择书仅用O()次比较,于是内部合并时间O(n)=O(),它与k无关,不再随k的增大而增大。
常见的有基于“败者树”的多路替代选择合并排序方法。
其他算法
外归并排序法并不是唯一的外排序算法。另外还有外分配排序,其原理类似于内排序中的桶排序。
在归并排序和桶排序之间存在数学上的某种对偶性。
此外还有一些不耗费附加磁盘空间的原地排序算法。
优化性能
计算机科学家吉姆·格雷的SortBenchmark网站用不同的硬件、软件环境测试了实现方法不同的多种外排序算法的效率。
效率较高的算法具有以下的特征:
并行计算
-
用多个磁盘驱动器并行处理数据,可以加速顺序磁盘读写。
-
在计算机上使用多线程,可在多核心的计算机上得到优化。
-
使用异步输入输出,可以同时排序和归并,同时读写。
-
使用多台计算机用高速网络连接,分担计算任务。
提高硬件速度
-
增大内存,减小磁盘读写次数,减小归并次数。
-
使用快速的外存设备,比如15000 RPM的硬盘或固态硬盘。
-
使用性能更优良个各种设备,比如使用多核心CPU和延迟时间更短的内存。
提高软件速度
-
对于某些特殊数据,在第一阶段的排序中使用基数排序。
-
压缩输入输出文件和临时文件。
内部排序
考虑到外部排序涉及的待排序记录数量大,可以采取分治的思想(即先分解, 再递归求解, 然后合并) 将其划分成几段合适的待排序记录,然后对每一小段采用内部排序方法。
换句话说,就是将外部排序转化为内部排序,所以为了进一步研究外部排序, 需先对内部排序进行深入的讨论。如果在排序过程中依据不同原则对内部排序方法进行分类,则大致可分为插入排序、冒泡排序、选择排序、归并排序和快速排序等5类。
通常, 排序记录存储具有如下3种形式:
1、待排序的一组记录存放在地址连续的一组存储单元上,它类似于线性表的顺序存储结
构,在序列中相邻的2个记录Rj 和R j+ 1 ( j = 1, 2,……, n - 1) 其存储位置也相邻。这种存储方式中,记录之间的次序关系由其存储的位置决定,排序通过移动记录来实现。
2、一组待排序记录存放在静态链表中,记录之间的次序关系由指针指示, 则实现排序不需要移动记录,仅需移动指针即可。
3、待排序记录本身存储在一组地址连续的存储单元内, 同时另设一个指示各个记录存储位置的地址向量, 在排序过程中不移动记录本身,而移动地址向量中这些记录的地址, 在排序结束之后再按照地址向量中的值调整记录的存储位置。
java 实现1
基本思路
首先将文件分割一个个小的文件,对于每个小的文件的内容使用普通的排序方法进行排序,所有的文件排序完毕后,对这些文件两两合并(使用归并的排序的思想进行合并)。
最后形成排完序的文件。
java 实现
[java]
import java.io.*;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Random;
/**
* 对于一个大文件进行排序
* Created by GGM on 2016/9/22.
*/
public class BigFileSort {
private static final int SPILT_SIZE = 10 * 10000;
private String parentPath;
private String filename;
public void sort(String fileName){
if (fileName == null || fileName.length() <= 0){
System.out.println("The filename is invalid");
return;
}
this.filename = fileName;
createDirSaveSplitFile(fileName);
splitFile(fileName);
//删除原文件
File f = new File(fileName);
f.delete();
//合并文件
try {
mergeFiles(0);
} catch (IOException e) {
e.printStackTrace();
}
deleteDirs();
}
private void deleteDirs() {
File file = new File(parentPath + "\\tmp0\\");
file.delete();
file = new File(parentPath + "\\tmp1\\");
file.delete();
}
private void mergeFiles(int level) throws IOException {
int mergeIndex = level;
int saveIndex = 1 - mergeIndex;
File mergeDir = new File(parentPath + "\\tmp" + mergeIndex + "\\");
File[] files = mergeDir.listFiles();
if (files == null || files.length <= 0) return;
if (files.length == 1){
copyFile(files[0], this.filename);
files[0].delete();
}
else if (files.length == 2){
megeTwoFiles(this.filename, files[0], files[1]);
files[0].delete();
files[1].delete();
}else{
int index = 0;
int i;
for (i = 0; i < files.length - 1; i += 2){
String fileName = parentPath + "\\tmp" + saveIndex + "\\tmp_" + index++;
megeTwoFiles(fileName, files[i], files[i+1]);
files[i].delete();
files[i+1].delete();
}
if (i == files.length - 1){
copyFile(files[i], parentPath + "\\tmp" + saveIndex + "\\tmp_" + index++);
files[i].delete();
}
mergeFiles(1-level);
}
}
private void copyFile(File file, String fileName) throws IOException {
File file1 = new File(fileName);
BufferedReader reader1 = new BufferedReader(new FileReader(file));
BufferedWriter writer = new BufferedWriter(new FileWriter(file1));
String n1;
n1 = reader1.readLine();
while (n1 != null){
int num1 = Integer.parseInt(n1);
writer.write(num1+"");
writer.newLine();
n1 = reader1.readLine();
}
reader1.close();
writer.close();
}
private void megeTwoFiles(String filenamem, File file1, File file2) throws IOException {
File file = new File(filenamem);
BufferedReader reader1 = new BufferedReader(new FileReader(file1));
BufferedReader reader2 = new BufferedReader(new FileReader(file2));
BufferedWriter writer = new BufferedWriter(new FileWriter(file));
String n1, n2;
n1 = reader1.readLine();
n2 = reader2.readLine();
while (n1 != null && n2 != null){
int num1 = Integer.parseInt(n1);
int num2 = Integer.parseInt(n2);
if (num1 <= num2) {
writer.write(num1+"");
writer.newLine();
n1 = reader1.readLine();
}else{
writer.write(num2+"");
writer.newLine();
n2 = reader2.readLine();
}
}
while (n1 != null){
int num1 = Integer.parseInt(n1);
writer.write(num1+"");
writer.newLine();
n1 = reader1.readLine();
}
while (n2 != null){
int num2 = Integer.parseInt(n2);
writer.write(num2+"");
writer.newLine();
n2 = reader2.readLine();
}
reader1.close();
reader2.close();
writer.close();
}
/**
* 创建临时文件存放目录
* @param fileName
*/
private void createDirSaveSplitFile(String fileName) {
File file = new File(fileName);
String fileParent;
if (file.isAbsolute()){
fileParent = file.getParent();
}else{
fileParent = new File(file.getAbsolutePath()).getParent();
}
parentPath = fileParent;
file = new File(fileParent + "\\tmp0\\");
if (!file.exists()) file.mkdir();
file = new File(fileParent + "\\tmp1\\");
if (!file.exists()) file.mkdir();
}
private void splitFile(String fileName) {
try {
BufferedReader br = new BufferedReader(new InputStreamReader(new FileInputStream(fileName)));
int i = 0;
int count = 0;
String num = "";
ArrayList list = new ArrayList<>();
while ( (num = br.readLine()) != null){
int number = Integer.parseInt(num);
list.add(number);
count++;
if (count == BigFileSort.SPILT_SIZE){
File file = new File(parentPath + "\\tmp0\\tmp_" + i++);
FileWriter writer = new FileWriter(file);
BufferedWriter bw = new BufferedWriter(writer);
Collections.sort(list);
for (Integer integer : list) {
bw.write(integer+"");
bw.newLine();
}
bw.close();
list.clear();
count = 0;
}
}
br.close();
} catch (FileNotFoundException e) {
e.printStackTrace();
} catch (IOException e) {
e.printStackTrace();
}
}
public static void main(String[] args) throws IOException {
File file = new File("D:\\test\\data.txt");
Random random = new Random((int)(Math.random() * 100));
FileWriter writer = new FileWriter(file);
BufferedWriter bw = new BufferedWriter(writer);
for (int i = 0; i < 1; i++){
for (int j = 0; j < 10000000; j++){
bw.write(random.nextInt(20000)+"");
bw.newLine();
}
}
bw.close();
new BigFileSort().sort("D:\\test\\data.txt");
file = new File("D:\\test\\data.txt");
BufferedReader br = new BufferedReader(new FileReader(file));
String line;
int count = 0;
while ((line = br.readLine()) != null){
System.out.print(line + " ");
count ++;
if (count == 50) {
System.out.println();
count = 0;
}
}
br.close();
}
}
排序算法2
[java]
public class SortWithMuchData {
public static void main(String[] args) throws Exception {
String fileIn = "C:\\Users\\xxx\\code\\java\\stu-project\\src\\main\\resources\\input.txt";
String fileOut = "C:\\Users\\xxx\\code\\java\\stu-project\\src\\main\\resources\\output.txt";
new Sort(fileIn, fileOut, 1000).run();
}
}
class Sort {
private final String fileIn;
private final String fileOut;
private int[] data;
private final int size;
private final List tempFiles;
public Sort(String fileIn, String fileOut, int size) {
this.fileIn = fileIn;
this.fileOut = fileOut;
this.data = new int[size];
this.size = size;
this.tempFiles = new ArrayList<>();
}
public void run() throws Exception {
System.out.println("begin...");
BufferedReader reader = new BufferedReader(new FileReader(fileIn));
String line;
int num = 0;
while ((line = reader.readLine()) != null) {
if (num < size) {
data[num] = Integer.parseInt(line);
num++;
} else {
sortAndSpill();
data = new int[size];
num = 0;
}
}
if (data.length > 0) {
sortAndSpill();
}
merge();
clear();
System.out.println("end...");
}
/**
* 合并临时文件
*/
private void merge() throws Exception {
new Merge(tempFiles, fileOut).run();
}
/**
* 清理临时文件
*/
private void clear() {
for (String tempFile : tempFiles) {
File file = new File(tempFile);
if (file.exists()) {
file.delete();
}
}
}
/**
* 数组排序,持久化
*/
private void sortAndSpill() throws IOException {
Arrays.sort(data);
spill();
}
/**
* 持久化临时文件
*/
private void spill() throws IOException {
String tempFileName = createTempFileName();
BufferedWriter writer = new BufferedWriter(new FileWriter(tempFileName));
for (int d : data) {
writer.write(String.valueOf(d));
writer.newLine();
}
writer.close();
System.out.println("生成临时文件:" + tempFileName);
tempFiles.add(tempFileName);
}
/**
* 生成临时文件名
*
* @return 临时文件名
*/
private String createTempFileName() {
return "C:\\Users\\yangshen\\code\\java\\stu-project\\src\\main\\resources\\" + UUID.randomUUID().toString() + ".txt";
}
static class Merge {
private int minValue;
private final int fileNum;
private final int[] tmpData;
private final BufferedReader[] readers;
private final String[] tempFiles;
private final BufferedWriter writer;
public Merge(List tempFiles, String fileOut) throws IOException {
this.minValue = -1;
this.fileNum = tempFiles.size();
this.tempFiles = tempFiles.toArray(new String[this.fileNum]);
this.tmpData = new int[this.fileNum];
this.readers = new BufferedReader[this.fileNum];
this.writer = new BufferedWriter(new FileWriter(fileOut));
init();
}
private void init() throws IOException {
for (int i = 0; i < tempFiles.length; i++) {
readers[i] = new BufferedReader(new FileReader(tempFiles[i]));
tmpData[i] = Integer.parseInt(readers[i].readLine());
}
}
public void run() throws IOException {
while (true) {
int ok = 0;
resetMinValue();
for (int i = 0; i < tmpData.length; i++) {
while (tmpData[i] == minValue) {
System.out.println(tmpData[i]);
write(String.valueOf(tmpData[i]));
fillTempData(i);
}
if (tmpData[i] == -1) {
ok++;
}
}
if (ok == fileNum) {
break;
}
}
writer.close();
}
/**
* 填充临时数组
*
* @param i 位置
*/
private void fillTempData(int i) throws IOException {
String line;
if ((line = readers[i].readLine()) != null) {
tmpData[i] = Integer.parseInt(line);
} else {
tmpData[i] = -1;
}
}
/**
* 写出
*
* @param item 写出内容
*/
private void write(String item) throws IOException {
writer.write(item);
writer.newLine();
}
/**
* 更新最小值
*/
private void resetMinValue() {
minValue = Arrays.stream(tmpData).filter(x -> x != -1).min().getAsInt();
}
}
}
参考资料
怎么排序超大文件![]() http://t.zoukankan.com/lightwindy-p-9650736.html
http://t.zoukankan.com/lightwindy-p-9650736.html
https://wenku.baidu.com/view/912105d47f1cfad6195f312b3169a4517723e5bd.html
处理大文件排序的方式–外部排序![]() https://blog.csdn.net/u012786993/article/details/119581205
https://blog.csdn.net/u012786993/article/details/119581205
简单实现大文件的排序和去重![]() http://www.muzhuangnet.com/show/82345.html
http://www.muzhuangnet.com/show/82345.html
https://www.it1352.com/2608282.html
https://blog.csdn.net/ggmfengyangdi/article/details/52627299
https://blog.csdn.net/ooeeerrtt/article/details/122545744