LeetCode刷题笔记【22】：回溯专题-5（递增子序列、全排列、全排列 II）

前置知识

参考前文

参考文章：
LeetCode刷题笔记【18】：回溯专题-1（回溯算法基础知识、用回溯算法解决组合问题）
LeetCode刷题笔记【19】：回溯专题-2（组合总和III、电话号码的字母组合）
LeetCode刷题笔记【20】：回溯专题-3（组合总和、组合总和II、分割回文串）
LeetCode刷题笔记【21】：回溯专题-4（复原IP地址、子集、子集II）

491.递增子序列

题目描述

LeetCode链接：https://leetcode.cn/problems/non-decreasing-subsequences/

错误思路, 踩的坑

回溯, 过程是**“遍历节点”**, 具体操作就是将上一个数通过函数参数传入, 判断当前数相比于上一个数是否增加;
如果增加, 加入path, 并加入ans;
很明显过程中涉及到"去重操作".
通过和前两天题目中的操作一样的i!=index && nums[i]==nums[i-1]来去重

class Solution {
private:
    vector<vector<int>> ans;
    vector<int> path;
    void backtrack(vector<int>& nums, int index, int pre){
        if(index>nums.size())
            return;
        if(path.size()>=2)
            ans.push_back(path);
        for(int i=index; i<nums.size(); ++i){
            if((i!=index && nums[i]==nums[i-1])
                || (path.size()!=0 && nums[i]<pre))
                continue;
            path.push_back(nums[i]);
            backtrack(nums, i+1, nums[index]);
            path.pop_back();
        }
        return;
    }
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtrack(nums, 0, INT_MIN);
        return ans;
    }
};

反思&正确思路

但是以上即使优化过, 但还是无法通过[1,2,3,4,5,6,7,8,9,10,1,1,1,1,1], 或者[4,4,3,2,1,4,4]
这是因为我们虽然做了去重检测, 但是只能去除连续的重复问题
在之前的一些题目里面, 我们这么做没有问题, 那是因为我们会先sort一遍

但是在本题中我们需要输入数组nums本身的顺序, 不能sort了
所以这个**“检测某个数字有没有在树的本层出现”**的功能, 就只能用unordered_set used来实现了

class Solution {
private:
    vector<vector<int>> ans;
    vector<int> path;
    void backtrack(vector<int>& nums, int index){
        if(index>nums.size())
            return;
        if(path.size()>=2)
            ans.push_back(path);
        unordered_set<int> used;
        for(int i=index; i<nums.size(); ++i){
            // if(used.count(nums[i]) || (path.size()!=0 && nums[i]
            //     continue;
            if(used.find(nums[i])!=used.end() || (!path.empty() && nums[i]<path.back()))
                continue;
            used.insert(nums[i]);
            path.push_back(nums[i]);
            backtrack(nums, i+1);
            path.pop_back();
        }
        return;
    }
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtrack(nums, 0);
        return ans;
    }
};

46.全排列

题目描述

LeetCode链接：https://leetcode.cn/problems/permutations/description/

用unordered_set used记录用过的数

思路: 还是回溯, 但是过程中用一个unordered_set used记录已经用了哪些数, 如果已经用过了就略过, 过程中在加入path的时候也加入used

class Solution {
private:
    vector<vector<int>> ans;
    vector<int> path;
    unordered_set<int> used;
    void backtrack(vector<int>& nums){
        if(nums.size()==path.size()){
            ans.push_back(path);
            return;
        }
        for(int i=0; i<nums.size(); ++i){
            if(used.find(nums[i]) != used.end())
                continue;
            used.insert(nums[i]);
            path.push_back(nums[i]);
            backtrack(nums, i+1);
            path.pop_back();
            used.erase(nums[i]);
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        backtrack(nums);
        return ans;
    }
};

用数组代替unordered_set

尝试用数组代替unordered_set

class Solution {
private:
    vector<vector<int>> ans;
    vector<int> path;
    void backtrack(vector<int>& nums, vector<bool>& used){
        if(nums.size()==path.size()){
            ans.push_back(path);
            return;
        }
        for(int i=0; i<nums.size(); ++i){
            if(used[i])
                continue;
            used[i] = true;
            path.push_back(nums[i]);
            backtrack(nums, used);
            path.pop_back();
            used[i] = false;
        }
    }
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        backtrack(nums, used);
        return ans;
    }
};

47.全排列 II

题目描述

LeetCode链接：https://leetcode.cn/problems/permutations-ii/description/

解题思路

参考上一题<46. 全排列>
原本的条件是**“不包含重复数字”, 现在是"可包含重复数字"**

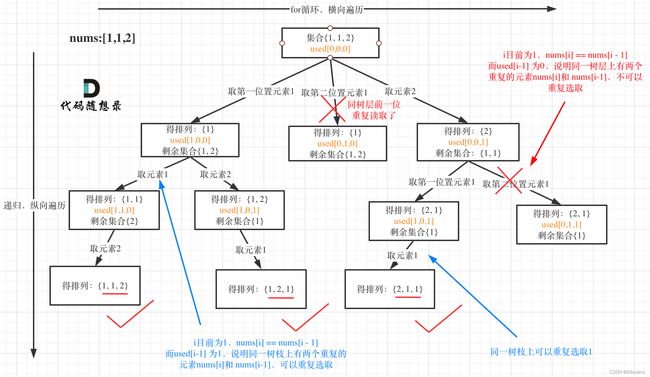
从图中可以看出: 我们需要"在同层中进行去重"
那么就需要一方面if(i>0 && nums[i]==nums[i-1] && !used[i-1]) continue;
另一方面一定要先sort.

代码

class Solution {
private:
    vector<vector<int>> ans;
    vector<int> path;
    void backtrack(vector<int>& nums, vector<bool>& used){
        if(path.size()==nums.size()){
            ans.push_back(path);
            return;
        }
        for(int i=0; i<nums.size(); ++i){
            if(i>0 && nums[i]==nums[i-1] && !used[i-1])// 这一层有多个相同的数, 目前处理的不是这些个中的第一个, 并且其中的第一个还没用呢
                continue;
            if(!used[i]){
                used[i] = true;
                path.push_back(nums[i]);
                backtrack(nums, used);
                used[i] = false;
                path.pop_back();
            }
        }
        return;
    }
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end());
        backtrack(nums, used);
        return ans;
    }
};

总结

回溯问题, 一方面模板大纲结构是确定的, 另一方面, 模板中的几个关键点需要注意:
① 是否需要去重, 如同层去重
1.1 要不要先sort
1.2 用used表 / 前后位比较
1.3 要不要先sort
② i=?
2.1 i=index
2.2 i=index+1
2.3 i=0
(这里也就也涉及是否要在参数中传递index)
③ 我们是要叶子节点还是遍历全部节点
3.1 最好先画一下树再决定
3.2 一般有套路, 但是具体到题目和解法, 可能会有多种做法
3.3 到终止条件后是否return

总而言之, 最好先画一下树用以理清思路, 并且注意过程中的这些关键点.
如果能记得清楚, 可以记一下不同类型的题目需要怎么做, 但不一定记得清楚, 所以最好还是画树和遍历结果, 具体问题具体分析.

本文参考：
递增子序列
全排列
全排列 II