恋上数据结构算法第三季总结
文章目录
-
- Something
-
-
- - 高效判断一个整数是否是奇数
-
- 线性表
-
-
- - 数组
- [75. 颜色分类](https://leetcode.cn/problems/sort-colors/)
- - 链表
- - 栈和队列
- [155. 最小栈](https://leetcode.cn/problems/min-stack/)
- [739. 每日温度](https://leetcode.cn/problems/daily-temperatures/)
- [654. 最大二叉树](https://leetcode.cn/problems/maximum-binary-tree/)
- - 动态规划 - DP(Dynamic Programming)
-
- 二叉树
- DFS - Depth First Search 深度优先搜索
- 高频题
-
-
- [283. 移动零](https://leetcode.cn/problems/move-zeroes/)
- [1. 两数之和](https://leetcode.cn/problems/two-sum/)
- [15. 三数之和](https://leetcode.cn/problems/3sum/)
- [50. Pow(x, n)](https://leetcode.cn/problems/powx-n/)
- [剑指 Offer 62. 圆圈中最后剩下的数字](https://leetcode.cn/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/)
- [54. 螺旋矩阵](https://leetcode.cn/problems/spiral-matrix/)
- [146. LRU 缓存](https://leetcode.cn/problems/lru-cache/)
- [7. 整数反转](https://leetcode.cn/problems/reverse-integer/)
- 252. 会议室
- 253. 会议室2
- [11. 盛最多水的容器](https://leetcode.cn/problems/container-with-most-water/)
- [42. 接雨水](https://leetcode.cn/problems/trapping-rain-water/)
-
- 刷题总结
Something
- 高效判断一个整数是否是奇数
boolean isOdd = (n & 1) == 1;
线性表
- 数组
-
绝大部分的数组排序题目中,用双指针或者三指针的方式便能很快很轻松的解决这个问题
-
很多时间复杂度是O(n2)或者O(n3)的解题方法,都可以思考用空间换时间的技巧去降低时间复杂度
- 后续的数组题都是用到了这个解题技巧
- 只是可能每个题具体的空间换时间的方法不太一样
- 但是空间换时间的思想都是一样的
-
双指针,用一个指针指向当前,用一个指针指向要交换的位置
-
三指针,用一个指针指向当前,一个指向开始,一个指向末尾
-
题目:
-
75. 颜色分类
public static void sortColors(int[] nums) { if (nums == null || nums.length == 0) return; int curP = 0; int zeroP = 0; int twoP = nums.length - 1; while (curP <= twoP) { if (nums[curP] == 2) { nums[curP] = nums[twoP]; nums[twoP--] = 2; } else if (nums[curP] == 0) { nums[curP++] = nums[zeroP]; nums[zeroP++] = 0; } else { curP++; } } } -
88. 合并两个有序数组
public static void merge(int[] nums1, int m, int[] nums2, int n) { if (nums1 == null || nums1.length == 0 || nums2 == null || nums2.length == 0) return; int i1 = m - 1; int i2 = n - 1; int cur = nums1.length - 1; while (i2 >= 0) { if (i1 >= 0 && nums1[i1] > nums2[i2]) { nums1[cur--] = nums1[i1--]; } else { nums1[cur--] = nums2[i2--]; } } } -
面试题 16.16. 部分排序
public static int[] subSort(int[] array) { if (array == null || array.length == 0) return new int[]{-1, -1}; int i = 1; int m = -1; int max = array[0]; while (i < array.length) { if (array[i] < max) { m = i; } else if (array[i] > max) { max = array[i]; } i++; } if (m == -1) return new int[]{-1, -1}; i = array.length - 2; int n = -1; int min = array[array.length - 1]; while (i >= 0) { if (array[i] > min) { n = i; } else if (array[i] < min) { min = array[i]; } i--; } return new int[]{n, m}; } -
977. 有序数组的平方
static public int[] sortedSquares(int[] nums) { if (nums == null || nums.length == 0) return nums; int[] sortedNums = new int[nums.length]; int begin = 0; int end = nums.length - 1; int cur = end; while (begin <= end) { int beginNum = nums[begin]; if (beginNum < 0) { beginNum = -beginNum; } int endNum = nums[end]; if (endNum < 0) { endNum = -endNum; } if (beginNum > endNum) { sortedNums[cur--] = beginNum * beginNum; begin++; } else { sortedNums[cur--] = endNum * endNum; end--; } } return sortedNums; }
-
-
-
- 链表
-
和数组一样,链表的题目绝大部分也是用多指针的方式解决
-
求中间节点
-
用快慢指针即可
- 快慢两指针同时从head出发
- 快的每次走两步
- 慢的每次走一步
- 当快的走到空的时候,那么此时慢的就是在中间
- 原理是:快的是慢的速度两倍
// 快慢指针找中间节点 // 两指针从初试位置出发 // 快指针走两步 慢指针走一步 // 当快指针为null的时候,慢指针此时指向的就是中间节点 ListNode middleNode(ListNode head) { ListNode fast = head; ListNode slow = head; while (fast.next != null && fast.next.next != null) { fast = fast.next.next; slow = slow.next; } return slow; }
-
-
反转链表
-
新建一个空节点newHead
- 从第一个节点head开始遍历
- 遍历到一个节点,先用一个tmp保存当前节点的next
- 将当前节点的next指向newHead
- 将newHead的next指向head
- 最后,head指向tmp即可
ListNode revert(ListNode head) { if (head == null || head.next == null) return head; ListNode cur = head; ListNode newHead = new ListNode(0); while (cur != null) { ListNode nextNode = cur.next; ListNode tmpNode = cur; tmpNode.next = newHead.next; newHead.next = tmpNode; cur = nextNode; } return newHead.next; }
-
-
题目
-
160. 相交链表
- 解题思路:将AB链表首位相连接
-
A链表的尾部链接B链表的头部
-
B链表的尾部链接A链表的头部
-
这样就让两个链表的长度一致
-
再分别从AB的头结点一次扫描
-
遇到的第一个都相等的节点的就是答案
-
- 解题思路:将AB链表首位相连接
-
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) return null;
ListNode nodeA = headA;
ListNode nodeB = headB;
while (nodeA != nodeB) {
nodeA = (nodeA == null) ? headB : nodeA.next;
nodeB = (nodeB == null) ? headA : nodeB.next;
}
return nodeA;
}
public ListNode getIntersectionNode1(ListNode headA, ListNode headB) {
if (headA == null || headB == null) return null;
ListNode nodeA = headA;
ListNode nodeB = headB;
boolean isHeadAConnected = false;
boolean isHeadBConnected = false;
while (nodeA != nodeB) {
if (nodeA == null && !isHeadAConnected) {
nodeA = headB;
isHeadAConnected = true;
} else {
nodeA = nodeA.next;
}
if (nodeB == null && !isHeadBConnected) {
nodeB = headA;
isHeadBConnected = true;
} else {
nodeB = nodeB.next;
}
}
return nodeA;
}
-
2. 两数相加
- 解法:就是正常的小学学的两数相加的方法
// 这个方法也是解决大数相加的一个方法
public static ListNode addTwoNumbers(ListNode l1, ListNode l2) {
if (l1 == null) return l2;
if (l2 == null) return l1;
ListNode dummyHead = new ListNode(0);
ListNode cur = dummyHead;
int carry = 0;
while (l1 != null || l2 != null) {
int val1 = l1 == null ? 0 : l1.val;
int val2 = l2 == null ? 0 : l2.val;
int sum = val1 + val2 + carry;
if (sum > 9) {
carry = 1;
sum = sum % 10;
} else {
carry = 0;
}
cur.next = new ListNode(sum);
cur = cur.next;
l1 = l1 == null ? l1 : l1.next;
l2 = l2 == null ? l2 : l2.next;
}
// 如果最后两位相加结果还有进位的话,这时候需要再新建一个节点
if (carry == 1) {
cur.next = new ListNode(1);
}
return dummyHead.next;
}
```
- [203. 移除链表元素](https://leetcode.cn/problems/remove-linked-list-elements/)
- https://leetcode.cn/problems/remove-linked-list-elements/
- 这题很简单,不赘述
```java
public static ListNode removeElements(ListNode head, int val) {
if (head == null) return head;
ListNode newNode = new ListNode();
ListNode curNode = newNode;
while (head != null) {
if (head.val != val) {
curNode.next = head;
curNode = curNode.next;
}
head = head.next;
}
curNode.next = null;
return newNode.next;
}
-
234. 回文链表
- 解题思路
-
先找到中间节点
-
再反转后半部分节点
-
之后从中间节点开始向两边扩散遍历
-
最后再恢复后半部分节点
-
- 解题思路
public boolean isPalindrome(ListNode head) {
if (head == null || head.next == null) return true;
if (head.next.next == null) return head.val == head.next.val;
ListNode middleNode = middleNode(head);
ListNode revertedNode = revert(middleNode.next);
while (revertedNode != null) {
if (head.val != revertedNode.val) {
return false;
}
head = head.next;
revertedNode = revertedNode.next;
}
return true;
}
// 快慢指针找中间节点
// 两指针从初试位置出发
// 快指针走两步 慢指针走一步
// 当快指针为null的时候,慢指针此时指向的就是中间节点
ListNode middleNode(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while (fast.next != null && fast.next.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
// 反转链表
ListNode revert(ListNode head) {
if (head == null || head.next == null) return head;
ListNode cur = head;
ListNode newHead = new ListNode(0);
while (cur != null) {
ListNode nextNode = cur.next;
ListNode tmpNode = cur;
tmpNode.next = newHead.next;
newHead.next = tmpNode;
cur = nextNode;
}
return newHead.next;
}
-
86. 分隔链表
- 解题思路
- 用两个链表存储大于和小于x的节点,循环完了之后再将两个链表相连
- 解题思路
// 思路:用两个链表存储大于和小于x的节点,循环完了之后再将两个链表相连
public static ListNode partition(ListNode head, int x) {
if (head == null) return null;
ListNode resultNode = new ListNode(0);
ListNode curNode = resultNode;
ListNode rightNode = new ListNode(0);
ListNode curRightNode = rightNode;
while (head != null) {
if (head.val < x) {
curNode.next = head;
curNode = curNode.next;
} else {
curRightNode.next = head;
curRightNode = curRightNode.next;
}
head = head.next;
}
curRightNode.next = null;
curNode.next = rightNode.next;
return resultNode.next;
}
- 栈和队列
-
题目
-
155. 最小栈
- 解法
- 提供一个属性保存当前最小值
- 在push和pop的时候检测和更新最小值即可
- 解法
-
private List<Integer> list = new ArrayList<>();
private int minVal;
public MinStack() {
this.minVal = Integer.MAX_VALUE;
}
public void push(int val) {
list.add(val);
if (val < this.minVal) {
this.minVal = val;
}
}
public void pop() {
int val = list.remove(list.size() - 1);
if (val == this.minVal) {
this.minVal = Integer.MAX_VALUE;
for (int i = 0; i < list.size(); i++) {
int v = list.get(i);
if (v < this.minVal) {
this.minVal = v;
}
}
}
}
public int top() {
return list.get(list.size() - 1);
}
public int getMin() {
return this.minVal;
}
-
239. 滑动窗口最大值 - 重点
-
采用双端队列
-
核心原理
- 保证当前队头元素是最大值
- 因此也叫做单调队列
-
复杂度O(n)
-
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums == null || nums.length == 0 || k < 1) return null;
if (k == 1) return nums;
// 用于保存index
Deque<Integer> queue = new LinkedList<>();
queue.add(0);
int[] result = new int[nums.length + 1 - k];
// 记录当前队列的队头位置
int begin = 0;
for (int i = 1; i < nums.length; i++) {
// i即为当前队列的队尾
begin = i + 1 - k;
int num = nums[i];
// 移除比num小的index, 使队列为单调队列
while (!queue.isEmpty() && nums[queue.getLast()] < num) {
queue.removeLast();
}
queue.add(i);
// 移除不在队列中的index
if (queue.getFirst() < begin) {
queue.removeFirst();
}
// 将最大值进行存放
if (begin >= 0) {
result[begin] = nums[queue.getFirst()];
}
}
return result;
// 字符串和链表很常考
}
-
739. 每日温度
- 采用栈 - 这个代码必须能默写出来
- 面试频率较高
- 类似的题
- 求数组中右边第一个比当前大的值
- 求数组中左边第一个比当前大的值
public int[] dailyTemperatures(int[] temperatures) { if (temperatures == null || temperatures.length == 0) return null; int[] result = new int[temperatures.length]; // 这是一个单调递减栈 Stack<Integer> stack = new Stack<>(); for (int i = 0; i < temperatures.length; i++) { while (true) { if (stack.isEmpty()) { stack.push(i); break; } if (temperatures[i] <= temperatures[stack.peek()]) { stack.push(i); break; } else { // 当当前值比top的大,pop出来的时候,当前值就是右边第一个比此时pop出来的值大的值 Integer idx = stack.pop(); result[idx] = i - idx; } } } return result; } -
654. 最大二叉树
- 和上面这个题同样解法
- 只是还需要求出左边第一个比他大的值
- 动态规划 - DP(Dynamic Programming)
-
绝大部分情况下,求最值都可以优先考虑用动态规划来实现
-
剑指 Offer 47. 礼物的最大价值
public int maxValue(int[][] grid) { int r = grid.length > 1 ? 2 : 1; int[][] maxRowVals = new int[r][grid[0].length]; // 当前row和前一个row // 主要用于刷新和记录已计算的之前两行的最大值 int curRow = 0; int preRow = 0; // 动态规划求解 // 从最左边开始,一次向右和向下遍历 // 将遍历到的当前val计算出其最大值,之后存储 /* 求解思路: * 当前的最大值 = 当前值 + max(当前行前一行最大值, 当前列前一列最大值) * */ for (int row = 0; row < grid.length; row++) { for (int col = 0; col < grid[0].length; col++) { if (row == 0) { maxRowVals[0][col] = col == 0 ? grid[0][0] : maxRowVals[0][col - 1] + grid[0][col]; } else { curRow = row & 1; preRow = 1 - curRow; if (col == 0) { maxRowVals[curRow][col] = grid[row][col] + maxRowVals[preRow][col]; } else { maxRowVals[curRow][col] = Math.max(maxRowVals[preRow][col], maxRowVals[curRow][col -1]) + grid[row][col]; } } } } return maxRowVals[curRow][grid[0].length - 1]; }-
121. 买卖股票的最佳时机
-
最优解,类似dp解法
/* * 这种解法类似动态规划解决 * 但是也可以用动态规划解决,但是没这种的效率高 * 这种问题直接求出以每一个位置的数值结尾时的最大利益值 * 之后保存这个最大利益值,将每次求出的最大利益值,跟当前求出的最大利益值比较 * 即可求出最终的最大值 * */ public class _121_买卖股票的最佳时机 { public int maxProfit(int[] prices) { if (prices == null || prices.length == 0 || prices.length == 1) return 0; int len = prices.length; int max = 0; int min = prices[0]; for (int i = 1; i < len; i++) { if (prices[i] < min) { min = prices[i]; } else { int tmpMax = prices[i] - min; if (tmpMax > max) { max = tmpMax; } } } return max; } } -
也可用dp解法,但是没上一种更优
- 思路:将每个数值之间的差值算出来,得出一个差值数组,最后的解就是求其最大连续子序列和
-
-
72编辑距离 - 重要经典的一个题
-
经典的dp解法
- 这比较复杂,但是确实经典的dp解法
public int minDistance(String word1, String word2) { char[] chars1 = word1.toCharArray(); char[] chars2 = word2.toCharArray(); // 新增一个dp数组,大小为n + 1和m + 1的二维数组, 用于存储转换结果 // 因此,dp[i][j]即为最终结果 // 例如,dp[word1.length - 1][word2.length - 1]即为这个题的解 int len1 = word1.length() + 1; int len2 = word2.length() + 1; int[][] dp = new int[len1][len2]; // 先将0行0列的dp赋值 // 很明显,都是非空字符串转空串,或者空串转字非空符串 // 因此,结果即是:非空串长度为多长,则最短进行多少次 for (int i = 0; i < len2; i++) { dp[0][i] = i; } for (int i = 1; i < len1; i++) { dp[i][0] = i; } for (int i = 1; i < len1; i++) { for (int j = 1; j < len2; j++) { // 这里有三种情况 // 算出三种情况,求出最小值即可 int min1, min2 ,min3 = 0; // 1.求dp[i - 1][j - 1]和dp[i][j]之间的转换方程 if (chars1[i - 1] == chars2[j - 1]) { // 当i和j最后一个字符相同的时候 min1 = dp[i - 1][j - 1]; } else { // 当i和j最后一个字符不相同的时候 min1 = 1 + dp[i - 1][j - 1]; } // 2.求dp[i - 1][j]和dp[i][j]之间的转换方程 min2 = 1 + dp[i - 1][j]; // 2.求dp[i][j - 1]和dp[i][j]之间的转换方程 min3= 1 + dp[i][j - 1]; dp[i][j] = Math.min(Math.min(min1, min2), min3); } } return dp[len1 - 1][len2 - 1]; }
-
-
5. 最长回文子串
-
经典dp解法
-
复杂度O(n^3)
// dp解法,但不是最优解,复杂度是O(n^3) public String longestPalindrome(String s) { int len = s.length(); if (len == 1) return s; char[] chars = s.toCharArray(); boolean[][] dp = new boolean[len][len]; int begin = 0; int maxLen = 0; for (int i = len - 1; i >= 0; i--) { for (int j = i; j < len ; j++) { if (j + 1 - i <= 2) { dp[i][j] = chars[i] == chars[j]; } else { dp[i][j] = dp[i + 1][j - 1] && (chars[i] == chars[j]); } int tmpMax = j + 1 - i; if (dp[i][j] && tmpMax > maxLen) { maxLen = tmpMax; begin = i; } } } return new String(chars, begin, maxLen); }
-
-
中心扩展法
- 以遍历到的每个字符为中心,或者每个字符间隙为中心,同时向左向右遍历对比即可求出
- 复杂度O(n^2)
private int begin = 0; private int maxLen = 1; // 扩展中心法,这种方法效率高于dp法 // 以每个字符或者字符间隙为中心进行两边扩展 // 复杂度是O(n^2) public String longestPalindrome(String s) { int len = s.length(); if (len == 1) return s; begin = 0; maxLen = 1; char[] cs = s.toCharArray(); for (int i = 1; i < len; i++) { // 以间隙为中心 palindromeLength(cs, i - 1, i); // 以字符为中心 palindromeLength(cs, i - 1, i + 1); } return new String(cs, begin + 1, maxLen); } // 给出l左边和r右边 // 分别同时向左向右扫描对比,找出最长回文字串 // 并判断求出maxLen和begin private void palindromeLength(char[] cs, int l, int r) { while (l >= 0 && r < cs.length) { if (cs[l] != cs[r]) { break; } l--; r++; } if (r - l - 1 > maxLen) { maxLen = r - l - 1; begin = l; } }
-
-
二叉树
-
二叉树的绝大部分面试题都可以通过递归加遍历解决
-
236. 二叉树的最近公共祖先
- 递归
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if (root == null || root == p || root == q) return root; TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p, q); if (left != null && right != null) return root; return left != null ? left : right; } -
99. 恢复二叉搜索树
-
利用BST特性: 中序遍历结果是升序的来解
- 当从中序遍历结果中只找到一对逆序对的话,那么这两个错误的节点遍历结果就是挨在一起的, 那么只需将这个逆序对交换位置即可
- 当从中序遍历结果中找到两个逆序对的话,那么交互第一个逆序对的第一个节点和第二个逆序对的第二个节点即可


public class _99_恢复二叉搜索树 { TreeNode prev; TreeNode first; TreeNode sec; // Morris遍历,可以让空间复杂度是O(1),时间复杂度O(n) // 也叫 线索二叉树 public void recoverTree(TreeNode root) { if (root == null) return; TreeNode node = root; while (node != null) { if (node.left != null) { TreeNode pred = node.left; while (pred.right != null && pred.right != node) { pred = pred.right; } if (pred.right == null) { pred.right = node; node = node.left; } else { System.out.print(node.val + " "); if (prev != null && prev.val > node.val) { // 出现逆序对 sec = node; if (first == null) { first = prev; } } prev = node; pred.right = null; node = node.right; } } else { System.out.print(node.val + " "); if (prev != null && prev.val > node.val) { // 出现逆序对 sec = node; if (first == null) { first = prev; } } prev = node; node = node.right; } } int val = first.val; first.val = sec.val; sec.val = val; } public void recoverTree1(TreeNode root) { if (root == null) return; find(root); int val = first.val; first.val = sec.val; sec.val = val; } private void find(TreeNode node) { if (node == null) return; find(node.left); if (prev != null && prev.val > node.val) { // 出现逆序对 sec = node; if (first == null) { first = prev; } } prev = node; find(node.right); } }
-
DFS - Depth First Search 深度优先搜索
-
排列组合绝大部分都是可以用DFS解决
-
回溯, 递归都是会自动回溯的
-
剪枝
-
DFS最重要的几点
-
明白下一层能够选择什么
-
明白最后一层结束条件和最后一层做什么事情
-
明白达到什么条件进行回溯
-
-
_17_电话号码的字母组合
public class _17_电话号码的字母组合 { private char[][] lettersArray = { {'a', 'b', 'c'}, {'d', 'e', 'f'}, {'g', 'h', 'i'}, {'j', 'k', 'l'}, {'m', 'n', 'o'}, {'p', 'q', 'r', 's'}, {'t', 'u', 'v'}, {'w', 'x', 'y', 'z'} }; private char[] chars; private List<String> list; private char[] string; public List<String> letterCombinations(String digits) { if (digits == null) return null; list = new ArrayList<>(); chars = digits.toCharArray(); if (chars.length == 0) return list; string = new char[chars.length]; dfs(0); return list; } private void dfs(int idx) { // 先dfs最后一层 if (idx == chars.length) { list.add(new String(string)); return; } // 再做非最后一层的处理 char[] letters = lettersArray[chars[idx] - '2']; for (char c : letters) { string[idx] = c; dfs(idx + 1); } } } -
46. 全排列
public class _46_全排列 { private List<List<Integer>> list = new ArrayList<>(); public List<List<Integer>> permute(int[] nums) { if (nums == null) return null; if (nums.length == 0) return list; dfs(nums, 0); return list; } private void dfs(int[] nums, int idx) { if (nums.length == idx) { List<Integer> result = new ArrayList<>(); for (int num : nums) { result.add(num); } list.add(result); return; } for (int i = idx; i < nums.length; i++) { // 交换位置 swap(nums, idx, i); dfs(nums, idx + 1); // 必须再次交换,不然的话,就会出错,因为后续的交换必须在之前数字顺序的情况下进行交换才行 // 因此这里是还原之前的位置 swap(nums, idx, i); } } // 交换方法 private void swap(int[] nums, int i, int j) { int tmp = nums[i]; nums[i] = nums[j]; nums[j] = tmp; } } -
47. 全排列 II
public class _47_全排列II { private List<List<Integer>> list = new ArrayList<>(); public List<List<Integer>> permuteUnique(int[] nums) { if (nums == null) return null; if (nums.length == 0) return list; dfs(nums, 0); return list; } private void dfs(int[] nums, int idx) { if (idx == nums.length) { List<Integer> result = new ArrayList<>(); for (int num : nums) { result.add(num); } list.add(result); return; } for (int i = idx; i < nums.length; i++) { if (isRepeat(nums, idx, i)) continue; swap(nums, idx, i); dfs(nums, idx + 1); swap(nums, idx, i); } } // 判断重复数字操作 private boolean isRepeat(int[] nums, int idx, int i) { for (int j = idx; j < i; j++) { if (nums[i] == nums[j]) return true; } return false; } private void swap(int[] nums, int i, int j) { int tmp = nums[i]; nums[i] = nums[j]; nums[j] = tmp; } } -
22. 括号生成
public class _22_括号生成 { private List<String> list = new ArrayList<>(); private char[] result; public List<String> generateParenthesis(int n) { if (n < 0) return list; result = new char[n*2]; dfs(0, n, n); return list; } private void dfs(int idx, int leftRemain, int rightRemain) { if (idx == result.length) { list.add(new String(result)); System.out.println(result); return; } // 这两个if就是之前常见的for循环 // 只是拆开成了两个单独的出来而已 if (leftRemain > 0) { result[idx] = '('; // 这里必须是在dfs的时候传参leftRemain - 1 // 而不是dfs之前leftRemain-- // 因为这里leftRemain--的话,就会让下面执行右括号的时候,leftRemain少了1 dfs(idx + 1, leftRemain - 1, rightRemain); } // 这里的idx和上面的idx是一样的 // 因此他们是平行关系 if (leftRemain != rightRemain && rightRemain > 0) { result[idx] = ')'; // 这里必须是在dfs的时候传参rightRemain - 1 // 而不是dfs之前rightRemain-- dfs(idx + 1, leftRemain, rightRemain - 1); } } }
高频题
283. 移动零
-
思路: 从左到右扫描,将非零的数字往前移动即可
-
时间复杂度: O(n)
-
空间复杂度: O(1)
public void moveZeroes(int[] nums) { if (nums == null || nums.length <= 1) return; int start = 0; int zeroCount = 0; // 先将所有非零数字向最左边移动 for (int i = 0; i < nums.length; i++) { if (nums[i] != 0) { nums[start++] = nums[i]; } else { // 记录下0的个数 zeroCount++; } } // 再将所有的零放在数组的最后 for (int i = nums.length - 1; i >= nums.length - zeroCount; i--) { nums[i] = 0; } }
1. 两数之和
- 方法1:暴力法,时间复杂度O(n^2) - 不推荐
- 方法2: 空间换时间,用哈希表存储之前扫描过的值, 时间复杂度O(n), 空间复杂度O(n)
- 很多时候可以多想想空间换时间的方法
public int[] twoSum(int[] nums, int target) {
int idx1 = -1;
int idx2 = -1;
// 用HashMap记录之前扫描过的值
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int remain = target - nums[i];
Integer hit = map.get(remain);
if (hit != null) {
idx1 = hit;
idx2 = i;
break;
}
map.put(nums[i], i);
}
int[] res = {idx1, idx2};
return res;
}
15. 三数之和
-
这道题比较麻烦
-
时间复杂度:O(n^2)
public List<List<Integer>> threeSum(int[] nums) { // 先排序 Arrays.sort(nums); List<List<Integer>> list = new ArrayList<>(); int l = 0; int r = 0; int len = nums.length - 2; int lastIdx = nums.length - 1; for (int i = 0; i < len; i++) { l = i + 1; r = lastIdx; if (i > 0 && nums[i] == nums[i - 1]) continue; while (l < r) { int sum = nums[i] + nums[l] + nums[r]; if (sum == 0) { list.add(Arrays.asList(nums[i], nums[l], nums[r])); // 跳过相等的值 while (l < r && nums[l] == nums[l + 1]) l++; while (l < r && nums[r] == nums[r - 1]) r--; // 往中间逼近 l++; r--; } else if (sum > 0) { r--; } else { l++; } } } return list; }
50. Pow(x, n)
-
解题方法:快速幂(分治)
-
解题法: 利用分治思想
// 递归法 public double myPow(double x, int n) { if (n == 0) return 1; // 判断是否是奇数的高效方法 boolean isOdd = (n & 1) == 1; double half = myPow(x, n / 2); half *= half; x = (n < 0) ? 1/x : x; return isOdd ? half * x : half; } // 快速幂 public double myPow1(double x, int n) { if (n == 0) return 1; double res = 1.0; while (n > 0) { if ((n & 1) == 1) { res *= n; } // 舍弃掉最后一位 n >>= 1; } return res; }
剑指 Offer 62. 圆圈中最后剩下的数字
-
就是约瑟夫环问题
-
环形链表, 但是面试中不适合用环形链表, 因为写一个环形链表相对比较复杂,因此用环形链表不现实
-
这个问题有数学规律可解
public class _剑指Offer62_圆圈中最后剩下的数字 { // 非递归 // 自下向上 // f(1, 3) = 0 // f(2, 3) = (f(1, 3) + 3) % 1 // ... // f(8, 3) = (f(7, 3) + 3) % 7 // f(9, 3) = (f(8, 3) + 3) % 8 // f(10, 3) = (f(9, 3) + 3) % 9 public int lastRemaining(int n, int m) { if (n == 1) return 0; int res = 0; int i = 1; while (i <= n) { res = (res + m) % i; i++; } return res; } // 递归方式 // 自顶向下 public int lastRemaining1(int n, int m) { if (n == 1) return 0; return (lastRemaining1(n - 1, m) + m) % n; } }
54. 螺旋矩阵
-
解题思路: 给定上下左右四个指针,一圈一圈的循环添加即可
-
public List<Integer> spiralOrder(int[][] matrix) { if (matrix == null) return null; List<Integer> list = new ArrayList<>(); if (matrix.length == 0) return list; int top = 0; int bottom = matrix.length - 1; int left = 0; int right = matrix[0].length - 1; while (left <= right && top <= bottom) { // left top -> right top for (int i = left; i <= right; i++) { list.add(matrix[top][i]); } top++; // right top -> right bottom for (int i = top; i <= bottom; i++) { list.add(matrix[i][right]); } right--; // 奇数行、偶数列的时候有问题 if (top > bottom || left > right) break; // right bottom -> left bottom for (int i = right; i >= left; i--) { list.add(matrix[bottom][i]); } bottom--; // left bottom -> left top for (int i = bottom; i >= top; i--) { list.add(matrix[i][left]); } left++; } return list; }
146. LRU 缓存
- 要实现put和get的O(1)时间复杂度
- 最近最少/最久使用问题
- 将最近最少使用的数据淘汰
- LRU缓存是操作系统常见的页面缓存淘汰机制
- 实现方式:哈希表 + 双向链表
- 哈希表用于存储数据,能实现put和get的O(1)时间复杂度
- 双向链表用于记录最近和最久使用情况,并且能实现记录和删除记录操作的O(1)时间复杂度
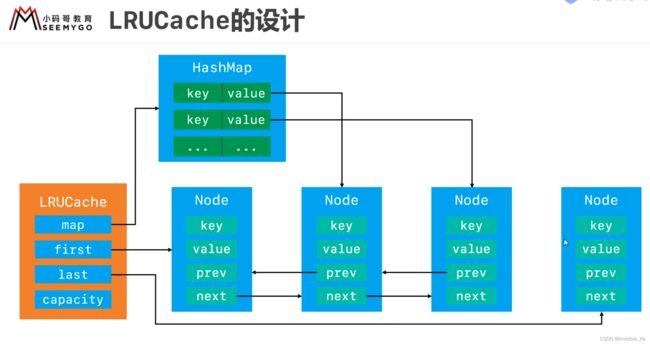
public class LRUCache {
private int capacity = 0;
private Map<Integer, Node<Integer, Integer>> map = new HashMap<>();
private Node<Integer, Integer> first;
private Node<Integer, Integer> last;
public LRUCache(int capacity) {
this.capacity = capacity;
this.first = new Node<>();
this.last = new Node<>();
first.next = last;
last.prev = first;
}
public int get(int key) {
Node<Integer, Integer> node = map.get(key);
if (node == null) return -1;
int v = node.value;
removeNode(node);
addAfterFirst(node);
return v;
}
public void put(int key, int value) {
Node<Integer, Integer> node = map.get(key);
if (node != null) {
node.value = value;
removeNode(node);
} else {
if (map.size() == capacity) {
removeNode(map.remove(last.prev.key));
}
node = new Node<>(key, value);
map.put(key, node);
}
addAfterFirst(node);
}
private void removeNode(Node<Integer, Integer> node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
private void addAfterFirst(Node<Integer, Integer> node) {
node.next = first.next;
first.next.prev = node;
node.prev = first;
first.next = node;
}
private class Node<K, V> {
public K key;
public V value;
public Node<K, V> prev;
public Node<K, V> next;
public Node(K key, V value) {
this.key = key;
this.value = value;
}
public Node() {}
}
}
7. 整数反转
- 解题方法
- 利用公式: res = res * 10 + x % 10
- 用long存储结果,就能存储int翻转后溢出的值了,这样就能判断是否溢出并赋值0
public int reverse(int x) {
// 用long存储,应对翻转后溢出的问题
long res = 0;
while (x != 0) {
res = res * 10 + x % 10;
// 判断是否溢出
if (res > Integer.MAX_VALUE || res < Integer.MIN_VALUE) {
res = 0;
break;
}
x = x / 10;
}
return (int) res;
}
252. 会议室
public boolean canAttendMeeting(int[][] meetings) {
if (meetings == null) return true;
if (meetings.length < 2) return true;
// 先排序
Arrays.sort(meetings, (m1, m2) -> {
return m1[0] - m2[0];
});
// 再比较
for (int i = 0; i < meetings.length - 1; i++) {
if (meetings[i][1] > meetings[i + 1][0]) return false;
}
return true;
}
253. 会议室2
-
实现方法
-
最小堆
-
最小堆获取top的时间复杂度是O(1),添加的时间复杂度是O(logn)
-
先对会议按照开始时间进行排序
-
将第一个会议室的结束时间添加进最小堆
-
遍历,如果,当前会议的开始时间小于最小堆的堆顶时间,那么将当前会议的结束时间添加进最小堆
-
如果,当前会议的开始时间大于等于最小堆的堆顶时间,那么移除堆顶元素,并将当前会议的结束时间添加进最小堆
-
遍历结束,那么最终最小堆中有多少个元素,就得开多少间会议室
public int minMeetingRooms(int[][] meetings) { if (meetings == null || meetings.length == 0) return 0; // 先对会议按照开始时间进行排序 Arrays.sort(meetings, (m1, m2) -> { return m1[0] - m2[0]; }); PriorityQueue<Integer> heap = new PriorityQueue<>(); heap.offer(meetings[0][1]); for (int i = 1; i < meetings.length; i++) { int[] meeting = meetings[i]; if (heap.peek() <= meeting[0]) { // 如果当前会议的开始时间大于等于堆顶的时间 // 那么就将当前堆顶时间移除 // 并将当前会议的结束时间添加进最小堆 heap.poll(); } // 否则就将当前会议的结束时间直接添加进最小堆 heap.offer(meeting[1]); } return heap.size(); }
-
分开排序
-
11. 盛最多水的容器
- 解题方法
- 一开始先让面积的长度最大
- 之后不断减小高度矮的那边, 这样字就可以省去很多没必要的计算
- 之后依次计算出square,比较出最大值
public int maxArea(int[] height) {
if (height == null || height.length < 2) return 0;
int l = 0;
int r = height.length - 1;
int maxSquare = 0;
// 一开始先让面积的长度最大
// 之后不断减小高度矮的那边, 这样字就可以省去很多没必要的计算
// 之后依次计算出square,比较出最大值
while (l < r) {
int square = (r - l) * Math.min(height[l], height[r]);
if (square > maxSquare) maxSquare = square;
if (height[l] > height[r]) {
r--;
} else {
l--;
}
}
return maxSquare;
}
42. 接雨水
-
解题方法
public int trap(int[] height) { if (height == null || height.length == 0) return 0; int sum = 0; int[] leftMaxes = new int[height.length]; int[] rightMaxes = new int[height.length]; // 求出左边最大值 // 并存放在数组中 // 当前index存放的值就是当前index时左边最大值 leftMaxes[0] = 0; for (int i = 1; i < height.length; i++) { leftMaxes[i] = Math.max(leftMaxes[i - 1], height[i - 1]); } // 求出右边最大值 // 并存放在数组中 // 当前index存放的值就是当前index时右边最大值 rightMaxes[height.length - 1] = 0; for (int i = height.length - 2; i >= 0; i--) { rightMaxes[i] = Math.max(rightMaxes[i + 1], height[i + 1]); } for (int i = 1; i < height.length - 1; i++) { // 当左边最大值和右边最大值都大于当前值的时候,才进行计算操作 if (leftMaxes[i] > height[i] && rightMaxes[i] > height[i]) { // 计算出当前柱子能装的水,并累加在sum中 int max = Math.min(leftMaxes[i], rightMaxes[i]) - height[i]; sum += max; } } return sum; }-
优化方法
- 可以不需要leftMaxes
- 因为计算每根柱子能装多少水的for循环也是从做往右开始的,因此可以将计算leftMax放在这个for里面即可
public int trap(int[] height) { if (height == null || height.length == 0) return 0; int sum = 0; int[] rightMaxes = new int[height.length]; // 求出右边最大值 // 并存放在数组中 // 当前index存放的值就是当前index时右边最大值 rightMaxes[height.length - 1] = 0; for (int i = height.length - 2; i >= 0; i--) { rightMaxes[i] = Math.max(rightMaxes[i + 1], height[i + 1]); } int leftMax = 0; for (int i = 1; i < height.length - 1; i++) { leftMax = Math.max(leftMax, height[i - 1]); // 当左边最大值和右边最大值都大于当前值的时候,才进行计算操作 if (leftMax > height[i] && rightMaxes[i] > height[i]) { // 计算出当前柱子能装的水,并累加在sum中 int max = Math.min(leftMax, rightMaxes[i]) - height[i]; sum += max; } } return sum; }
-
















