【科研论文配图绘制】task6直方图绘制
文章目录
- 【科研论文配图绘制】task6直方图绘制
-
- 1.直方图介绍
- 2.直方图使用场景
- 3.直方图示例
- 4.带正态分布曲线的直方图
【科研论文配图绘制】task6直方图绘制
task6 主要掌握直方图的绘制技巧,了解直方图含义,清楚统计指标的添加方式
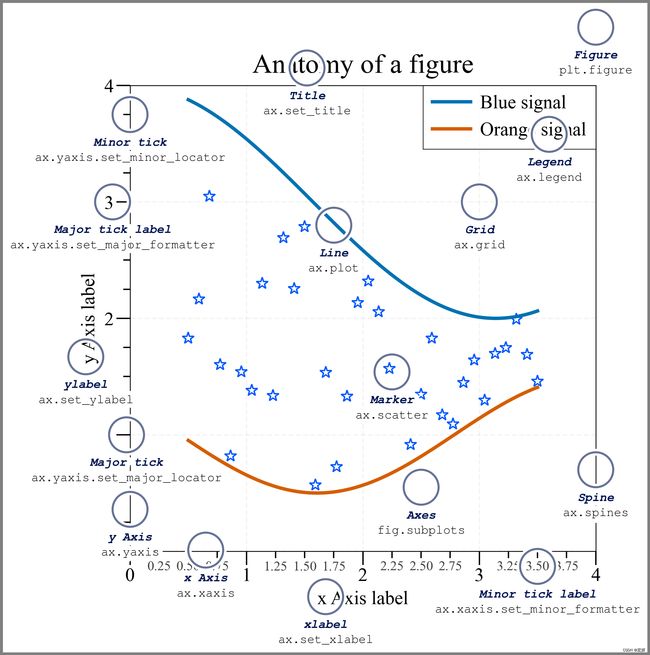
1.直方图介绍
直方图是一种用于表示数据分布情况的图形工具,通过将数据分成不同的区间(也称为“箱子”或“bin”),并计算落入每个区间的数据点数量或频数,从而展示数据的分布模式。直方图的横轴表示数据的范围,纵轴表示数据点的频数或相对频率。
绘制直方图的过程通常涉及将数据分组并计算每个区间的频数,然后将这些频数表示为柱状图。直方图的外观会受到区间宽度和数量的影响,因此合适的区间选择对于准确地反映数据分布至关重要。
当使用直方图进行数据分析时,以下是需要注意的几个重要事项:
选择适当的区间数量和宽度: 选择合适的区间数量和宽度对于正确显示数据分布至关重要。过多的区间可能导致图像复杂,过少的区间可能忽略细节。
了解数据含义: 在绘制直方图之前,理解数据的背景和含义。确保理解每个区间代表的实际值。
处理异常值: 在绘制直方图前,处理数据中的异常值。异常值可能影响直方图的形状和解释。
选择合适的展示方式: 选择适合的直方图类型,如频数直方图、相对频率直方图或累积频数直方图,以满足分析需求。
添加标签和注释: 确保图表包括轴标签、图例和标题,使观众能够理解图表内容。标签和注释应清晰明了。
避免误导: 避免通过调整区间或缩放来误导观众。确保图表准确地反映数据分布。
比较不同数据集: 如果要比较不同数据集,使用相同的区间和标尺,以便进行准确的对比分析。
2.直方图使用场景
直方图是一种常用的数据可视化工具,用于显示数据的分布情况。一般情况下,直方图在以下场景中被广泛应用:
数据分布分析: 直方图可以帮助您了解数据的分布情况,包括数据集中在哪个区间,是否呈现正态分布、偏态分布等特点。
数据异常检测: 通过观察直方图,您可以发现数据中是否存在异常值或者极端值。异常值可能会对整体数据分布产生影响。
特征工程: 在机器学习和数据分析中,直方图可以帮助您选择合适的特征变换或者分箱策略,以提高模型的性能。
决策支持: 在做决策时,直方图可以帮助您对数据有更深入的了解,从而做出更明智的决策。
数据预处理: 在数据清洗和预处理阶段,直方图可以帮助您识别数据缺失、离散化、标准化等问题。
直方图适用于分析数据的分布情况以及发现数据中的模式、特征和异常。根据需要,我们可以使用直方图来更好地理解数据,并为后续的分析和决策提供有价值的信息。
3.直方图示例
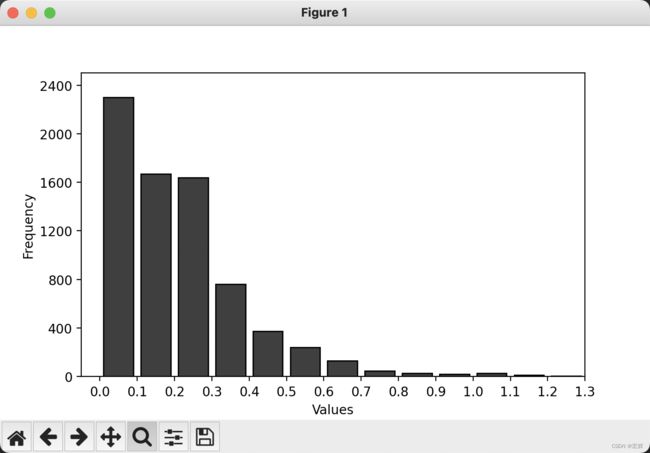
先上代码示例1:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 设置 matplotlib 参数,关闭 y 轴刻度在右侧
plt.rcParams["ytick.right"] = False
# 从 Excel 文件中读取数据
hist_data = pd.read_excel(r"data/单变量图表绘制/柱形图绘制数.xlsx")
# 从数据中提取 "hist_data" 列的值
hist_x_data = hist_data["hist_data"].values
# 定义直方图的箱子范围
bins = np.arange(0.0, 1.5, 0.1)
# 创建绘图区域和坐标轴
fig, ax = plt.subplots(figsize=(4, 3.5), dpi=100)
# 绘制直方图
hist = ax.hist(x=hist_x_data, bins=bins,
color="#3F3F3F", edgecolor='black',
rwidth=0.8)
# 设置 x 轴次刻度不显示在顶部和底部
ax.tick_params(axis="x", which="minor", top=False,
bottom=False)
# 设置 x 轴和 y 轴刻度值
ax.set_xticks(np.arange(0, 1.4, 0.1))
ax.set_yticks(np.arange(0., 2500, 400))
# 设置 x 轴和 y 轴的范围
ax.set_xlim(-.05, 1.3)
ax.set_ylim(0.0, 2500)
# 设置 x 轴和 y 轴的标签
ax.set_xlabel('Values')
ax.set_ylabel('Frequency')
# 显示图形
plt.show()
4.带正态分布曲线的直方图
利用 Python 绘制图所示的带统计信 息的直方图的难点在于正态分布曲线的计算和
绘制。我们可以使用 scipy.stats.norm() 函数对绘制数据实现正态拟合,计算出概率密度函数
图 3-2-2 带统计信息的直方图绘制示例 (Probability Density Function,PDF)结果。由于概率密度函数结果是归一化的,即曲线下方的面积为 1,而直方图的总面积是样本数和每个 bin 宽度的乘积,因此,对概率密度函数结果与样本个数、bin 宽度值相乘的结果进行绘制,即可将绘制的曲线缩放到直方图的高度。

示例代码2:
import numpy as np
import pandas as pd
from scipy.stats import norm
import matplotlib.pyplot as plt
# 从CSV文件读取数据
hist_data02 = pd.read_csv(r"data/单变量图表绘制/直方图绘制02.csv")
# 定义直方图的箱数
bins = 15
# 提取数据列作为绘图数据
hist_x_data = hist_data02["hist_data"].values
# 计算数据的中位数和均值、标准差
Median = np.median(hist_x_data)
mu, std = norm.fit(hist_x_data)
# 创建绘图区域和坐标轴
fig, ax = plt.subplots(figsize=(5, 3.5), dpi=100)
# 绘制直方图
hist = ax.hist(x=hist_x_data, bins=bins, color="gray",
edgecolor='black', lw=.5)
# 绘制正态分布曲线(Plot the PDF)
# 生成用于绘制曲线的 x 值
xmin, xmax = min(hist_x_data), max(hist_x_data)
x = np.linspace(xmin, xmax, 100)
# 计算正态分布的概率密度函数(PDF),这里的 mu 和 std 分别是数据的均值和标准差
p = norm.pdf(x, mu, std)
# 计算一个用于缩放曲线的因子,以使曲线在绘制区域内总面积与数据数量相匹配
N = len(hist_x_data)
bin_width = (x.max() - x.min()) / bins
# 绘制正态分布曲线
ax.plot(x, p * N * bin_width, linewidth=1, color="r",
label="Normal Distribution Curve")
# 添加均值线
ax.axvline(x=Median, ls="--", lw=1.2, color="b",
label="Median Line")
# 设置 x 轴和 y 轴标签
ax.set_xlabel('Values')
ax.set_ylabel('Count')
# 添加图例
ax.legend(frameon=False)
# 显示图形
plt.show()
上述代码将绘制一个直方图,将数据与拟合的正态分布曲线叠加在一起,并在图上添加中位数线和图例。该图可以帮助我们观察数据的分布情况以及是否符合正态分布。