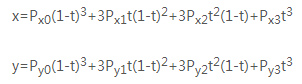前端动画之贝塞尔曲线推导及应用

hello，大家好，今天豆皮范儿给大家带来了贝塞尔曲线推导和应用，优美的贝塞尔曲线想起了大学时候老师在给我们讲如何实现，如何推导，如何实现和应用。本来也来详细介绍一下，纯纯的干货～

作者：lff

生活中总是会不自觉的画出来让我们觉得“和谐、平滑”的曲线，却不知道怎么形容。有些可能是在我们认知范围内的，可能是圆弧，抛物线，或者三角函数曲线，螺旋线。另外还有一些优美的，它们可以往任意方向延伸的曲线，各种各样，看上去很神秘，其实他们都可以用贝塞尔曲线来描述。如蜿蜒的河流，层叠的山峦，汹涌的波涛，大雁的翅膀在飞行运动中画出的美丽的贝塞尔曲线。所以贝塞尔曲线与自然相生，是透露着自然之美的曲线。

1962年，Bezier构造了一种以逼近为基础的参数曲线和曲面的设计方法。这个想法是基于在进行汽车外形设计时，先用折线段勾画出汽车的大致外形轮廓，然后用光滑的参数曲线去逼近这个折线多边形。这个折线多边形被称为特征多边形，逼近该特征多边形的曲线被称为Bezier曲线。

其实贝塞尔曲线并非是由贝塞尔发明的，只不过因为他把这个东西应用到当时的汽车领域而闻名的，所以取名为贝塞尔曲线。

Bezier方法将函数逼近同几何表示结合起来，贝塞尔曲线被广泛地应用于很多图形图像软件中，使得设计师在计算机上就像使用作图工具一样得心应手，很大程度上改善了计算机绘图的僵硬方式。如下图Photoshop的钢笔工具。

用简单的话来理解一下贝塞尔曲线，他是通过少量几个点，使用一套公式，生成一条平滑曲线。

生成贝塞尔曲线

那么如何创建贝塞尔曲线？

一次贝塞尔

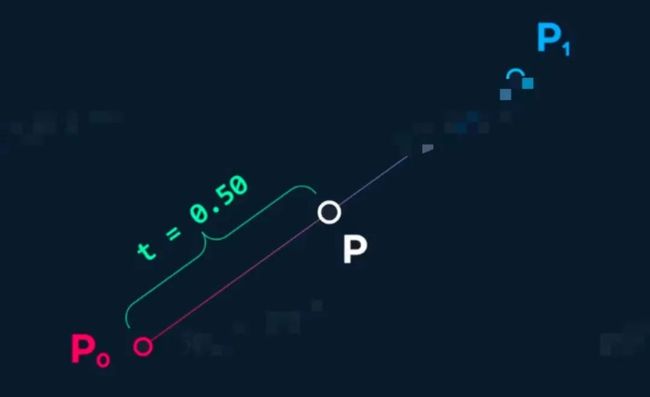
假如我们有两个点P0和P1，中间连线

现在加入第三个点P，位于两端点中间。通过t值来定义P的位置，t值范围从0-1

其公式为：

这个函数被称为线性插值（或Lerp）。

二次贝塞尔

现在我们添加另外一个点会怎么样呢？

我们会有两个插值点，每条线段都可以看做一个线性插值，需要做的就是保证两条线段上的t值保持一致。

然后我们可以将这两个插值点连接成一条新的线段。

在这条新的线段上我们同样使用线性插值，产生一个新点，该点也是基于相同t值得Lerp。这个点的轨迹，就是二次贝塞尔曲线。

整个过程的动画如下：

三次贝赛尔

再增加一个点，同理过程如下（得到一条三次贝塞尔曲线）：

我们增加的点可以在任意位置，只要遵循以上规则，便可绘制出一条贝塞尔曲线。但Bezier曲线不可对曲线形状进行局部控制，如果改变任一控制点位置，整个曲线会受到影响。

推导过程

我们以三次贝塞尔曲线为例：

A=Lerp(P0,P1,t)

B=Lerp(P1,P2,t)

C=Lerp(P2,P3,t)

D=Lerp(A,B,t)

E=Lerp(B,C,t)

P=Lerp(D,E,t)

可以看出，沿途每个新点都是由前两个点的Lerp计算得出，直到形成一条贝塞尔曲线。

综合解释，D点运动轨迹可以看作是P，P1，P2，三点组成的二次贝塞尔曲线，E点运动轨迹可以看作P1，P2，P3三点组成的二次贝塞尔曲线。因此，度数为n的贝塞尔曲线可以通过度数为n-1的两条贝塞尔曲线之间点对点的线性插值获得。

这种得出贝塞尔曲线的算法称为De Casteljau算法。 这种算法具有数值稳定性，简单好记。只需要不断采用Lerp函数来确定新的点。

---

让我们换一种方式重写各点的函数表达式：

A=(1-t)P0+tP1

B=(1-t)P1+tP2

C=(1-t)P2+tP3

D=(1-t)A+tB

E=(1-t)B+tC

F=(1-t)D+tE

我们将中间过程一步步带入表达式，充分扩展并经过整理变换后得出最终F点的函数表达式：

P(t)=

P0*(-t^3+3t^2-3t+1)+

P1*(3t^3-6t^2+3t)+

P2*(-3t^3+3t^2)+

P3*( t^3 )

这就是贝塞尔曲线的伯恩斯坦多项式形式。

他们中的每一项相乘的数值，都是一个关于t值的多项式。那么这四个多项式是长什么样子呢，我们来看图。横轴代表t的变换，从0-1，纵轴代表多项式的值，我们称作权重，因为权重w值的大小代表了P0-P3各点分别对最终结果起多大作用。

这四条曲线均为三次曲线，并且任何三次贝塞尔曲线都是这四条曲线的线形组合。不同之处只是起始点和控制点P0-P3的不同来决定了最终曲线的走向。

同时P(T)表达式中的每一项，都可以看成是基于原来的点的向量。看下图的动画，随着t的变化，他们的大小也在相应的调整。将四个向量首尾连接随着t值的变化，向量的终点随时间t形成的轨迹也就是贝塞尔曲线的轨迹。

贝塞尔曲线求导

我们对贝塞尔曲线函数求导：

P'(t)=

P0*(-3t^2+ 6t-3)+

P1*( 9t^2-12t+3)+

P2*(-9t^2+ 6t)+

P3*( 3t^2 )

对其求导有什么特殊的含义吗？大家都知道导数即某一点处切线的斜率是曲线在该点的变化率，即关于给定的曲线t值的速度向量。通过上面P'(t)的函数表达式，我们可以得出三次贝塞尔曲线的导函数是一条二次贝塞尔曲线。对于任意次的贝塞尔曲线都是这样的，其导数是另外一条贝塞尔曲线，次数-1。

我们求导数的意义和用途是什么呢？

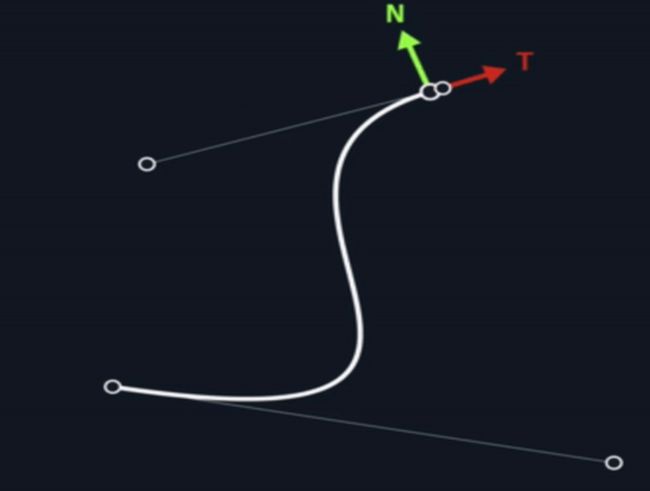
切线和法线

因为导数代表的是曲线的切线，那么我们知道了切线，再将其旋转90度（参考右手定则），也便得到了曲线的法线。一旦我们有了切线和法线的方向，我们就可以得到偏移指定距离的其他曲线的函数方程，该技术通常应用于道路设计。

此外，复杂曲线并不是仅仅一条贝塞尔曲线，而是由多条曲线连接形成，怎么使连接处光滑？就需要确保连接点位置的切线相同。这也是求切线的意义。

求曲率

二阶导数是一阶导数的导数。从原理上看，它表示一阶导数的变化率；从图形上看，它反映的是函数图像的凹凸性。

二阶导数代表的是曲线的曲率，曲率可以解释为半径的倒数，也就是数我们可以求出某一点处贝塞尔曲线内切圆的半径，结合法线，可以到得内切圆公式，当经过曲线拐点的时候，曲率为0，也就是没有内切圆。

这个过程可以帮助我们计算出曲线某点的弯曲程度。像无人驾驶车辆的运动规划，目标轨迹曲率是连续的且轨迹的曲率不超过车辆可行驶轨迹曲率的限制。

求包围盒

导数另外一个用途，可以帮助我们计算曲线的包围盒。

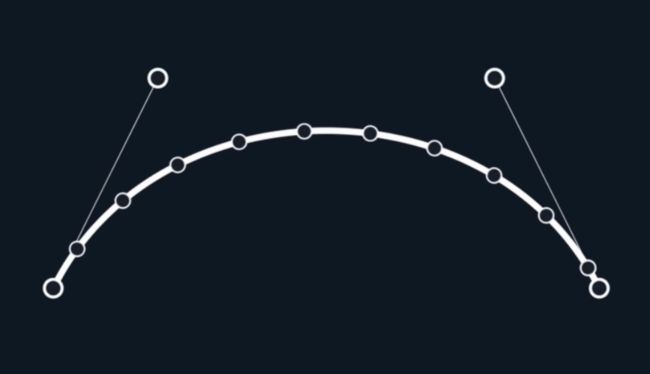
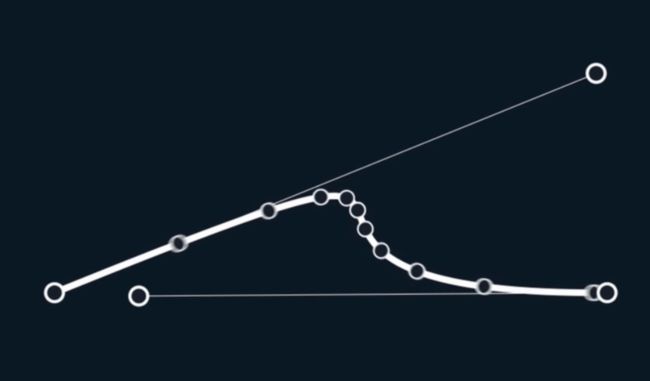
计算贝塞尔曲线的包围盒时，最简单的方式是将曲线的所有控制点和端点求出最大最小值。在某些时候是满足使用的，但我们真正想要的是最小边界框。很多情况下两者差距会很大，如下图：

如果我们想要找到边界框，这些点是我们想要知道的。

那么怎么计算这些点呢？

第一步，我们将曲线方程转化为x和y分别关于t的两个参数方程：

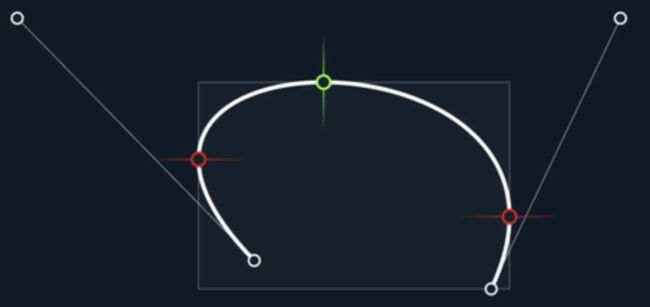
P0-P3三个点的(x, y)坐标值决定了曲线的样子。以下面这条三次贝塞尔曲线为例：

我们可以看到标记的极大值极小值，红点和绿点的位置与x，y曲线上标记的位置是一致的。这些极值点是对应导数改变符号的地方。

下面我们再来看下x和y两条曲线对应的导数曲线，他们的根便是我们正在寻找的极值处的t值。

具体计算方法：

前面我们已经得出三次贝塞尔曲线的导数公式，现在我们变换下顺序重新用t来表示它：

P'(t)=

t^2*(-3P0+9P1-9P2+3P3)+

t * ( 6P0-12P1+6*P2)+

(-3P0+ 3P1)

我们现在求这个导函数的根：

这给出我们四个潜在的t值：

根据t值带入贝塞尔函数，得出极值，再和两端点一起计算边界框的范围。

补充：我们再观察下这个动画展示过程，可以看出曲线的变化是怎么影响导函数曲线变化的，注意导函数曲线与x轴或y轴交点位置：

以上就是分析贝塞尔曲线边界框的过程。

求曲线长度

遗憾的是，贝塞尔虽然很常用，但并没有计算三次贝塞尔曲线长度的公式。

三次贝塞尔属于椭圆积分！通常，椭圆积分不能用基本函数表达，意味着解析法无解。

怎么解决，采用近似求解法：

要求出贝塞尔曲线的长度，我们理解了贝塞尔函数P(t)的定义，是指时间t时的位置，对它求导就可以得到t时刻的速度。按照微积分的思想，把如果把t分得很小，速度乘上时间得到路程，就可以用下面公式求得路程。

沿曲线设置动画

我们得到了整个贝塞尔曲线的弧长，那么我们在曲线上指定点，并根据它们为曲线设置动画。

我们可以设置相等间隔的t值，去计算出一个点。

我们看上面的动画，第一条贝塞尔曲线我们得到的点看上去是没什么问题的，如果我们设定动画，他也会匀速运动。

不过，当我们去改变控制点，发现情况变得糟糕了，指定点变得不规律，速度也不恒定。这是因为设定t值相等的间隔，对应计算出来的距离间隔并不均匀。我们其实想要的是间隔距离相等。

动画中第一条曲线只是比较特殊而已。但为什么会出现这种情况，导函数的曲线可以解释给我们。导数理解为点的速度，如果我们的点沿曲线以不同的速度移动，这意味着导数该点处的长度（速度向量的长度）在变化。

而第一条贝塞尔曲线的导数形成的曲线围绕原点几乎是个圆弧，这也就意味着速度是恒定的。但是改变控制点之后的贝塞尔曲线的导数曲线是如下情况，曲线上各点与原点的距离是在变化的：

那么怎么解决这个问题呢？

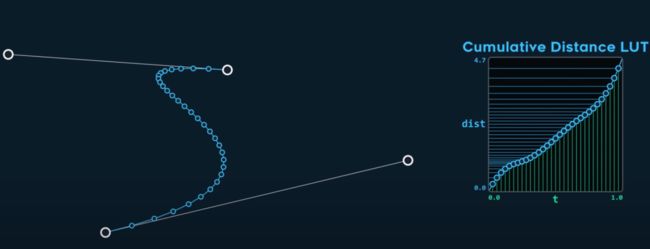
因为没有曲线长度的公式，我们仍然需要采用近似的方式，将曲线看着一条条直线连接而成，分的越多，和曲线越贴近：

再通过细分曲线生成一整t值对应曲线长度的查询表。这张表就记录了t沿着曲线对应的距离，这样给定距离值，我们就能从表中找到对应的t值。我们采样越多越密集，计算就越精确，但代价就越大。

应用案例

相信大家之前对贝塞尔曲线都不陌生，我们平时应用到的地方可能有：

• 绘制平滑的曲线• 定义动画运动轨迹• 过渡动画效果如：仿真翻页效果，按钮下拉粘连效果• CSS3中的动画（缓动函数，cubic-bezier(.17,.67,.83,.67) ✿ cubic-bezier.com）• 游戏应用（贪吃蛇，弯曲道路或者河流，炮弹的飞行轨迹等）。• 建筑应用：过山车，桥梁，道路等

下拉粘连动画：

绘制树干动画：

模拟烟花：

仿真翻页：

平滑曲线：

生成路径：

关注公众号的福利持续更新，公众号后台送学习资料：

1、豆皮范儿后台回复「vis」，还可以获取更多可视化免费学习资料。

2、豆皮范儿后台回复「webgl」，还可以获取webgl免费学习资料。

3、豆皮范儿后台回复「算法」，还可以获取算法的学习资料。

4、豆皮范儿后台回复「招聘」，获取各种内推。

点个赞，证明你还爱我

内推字节跳动，点击➡️阅读原文