C++进阶:哈希
哈希
1. unordered容器
当节点非常多时,map和set查询效率也不够理想。C++11新增unordered_map, unordered_set等底层为哈希的关联式容器。
unordered意为无序的,即存储遍历不按key排序。所以unordered系列容器只有单向迭代器。
| 容器 | 底层 | 区别 |
|---|---|---|
| set / map | 红黑树 | 排序加去重 |
| multiset / multimap | 红黑树 | 排序不去重 |
| unordered_set / unordered_map | 哈希 | 去重不排序 |
| unordered_multiset / unordered_multimap | 哈希 | 不排序不去重 |
1.1 效率对比
int n = 10000000;
vector<int> v;
srand((unsigned int)time(nullptr));
for (int i = 0; i < n; i++) {
v.push_back(rand());
v.push_back(i);
}
set<int> s;
unordered_set<int> us;
int begin1 = clock();
for (auto e : v) {
s.insert(e);
}
int end1 = clock();
//
int begin2 = clock();
for (auto e : v) {
us.insert(e);
}
int end2 = clock();
cout << "set insert: " << end1 - begin1 << endl;
cout << "unordered_set insert: " << end2 - begin2 << endl;
- 当插入随机值且数据量很大时,unordered_set比set快3倍左右。
- 当插入有序值且数据量很大时,unordered_set比set慢2倍左右。
- unordered_set的查找效率极高,这得益于哈希的底层结构。
set更适合有序重复度低的数据,unordered_set更适合随机重复度高的数据。综合来看,unordered系列容器比map/set效率要更好些。
2. 哈希
2.1 哈希的定义
哈希也叫做散列,记数排序就体现了哈希思想。
计数排序为统计数字出现的个数,为每个数字都开辟了对应的一块空间,用来记录其出现的个数,每遇到就加一。
将一个元素和一个位置建立映射关系,这就是哈希的本质。
哈希函数
搜索树中key与元素的存储位置没有直接映射。因此查找必须经历多次比较key。搜索效率还是不够理想。
最理想的搜索方法是:不经任何比较,一次性直接得出元素的存储位置。
通过某种函数(hashFunc)使元素 key 与它的存储位置之间能够建立映射关系,那么就可以一次性找到该元素。
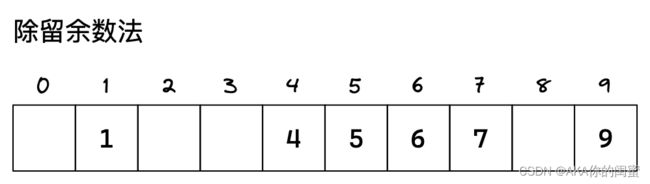
除留余数法
例如,存在数据集合 [ 1 , 7 , 6 , 4 , 5 , 9 ] [1,7,6,4,5,9] [1,7,6,4,5,9],将哈希函数设置为 h a s h ( k e y ) = k e y % c a p a c i t y hash(key)=key\;\%\;capacity hash(key)=key%capacity, c a p a c i t y capacity capacity 为存储空间总的大小。
自定义哈希函数
常见的数据类型如整数,库中自带哈希函数,但有些类型比如自定义类型,需要我们自定义哈希函数。
可以把哈希函数设计成仿函数,对不同类型添加特化处理。
template<class K>
struct Hash {
size_t operator()(const K& key) {
return key;
}
};
// 特化
template<>
struct Hash<string> {
//BKDR
size_t operator()(const string& s) {
size_t val = 0;
for (auto ch : s) {
val = val * 131 + ch;
}
return val;
}
};
如果我们自定义类型作key,可以单独为其设计一个哈希函数,并在创建哈希表时作参数传进去。
struct Date {
int _year;
int _month;
int _day;
};
struct HashDate {
size_t operator()(const Date& date) {
return date._year + date._month + date._day;
}
};
哈希冲突
很可能存在不同数值映射到同一位置的情况,比如 10 % 10 = 0 , 20 % 10 = 0 10\%10=0,\;20\%10=0 10%10=0,20%10=0。这就是哈希冲突或称哈希碰撞。
一般哈希冲突是不可避免的,冲突越多效率越低,故提高哈希效率在于如何解决哈希冲突。解决哈希冲突的两种常见的方法是:闭散列和开散列。
2.2 哈希冲突的解决
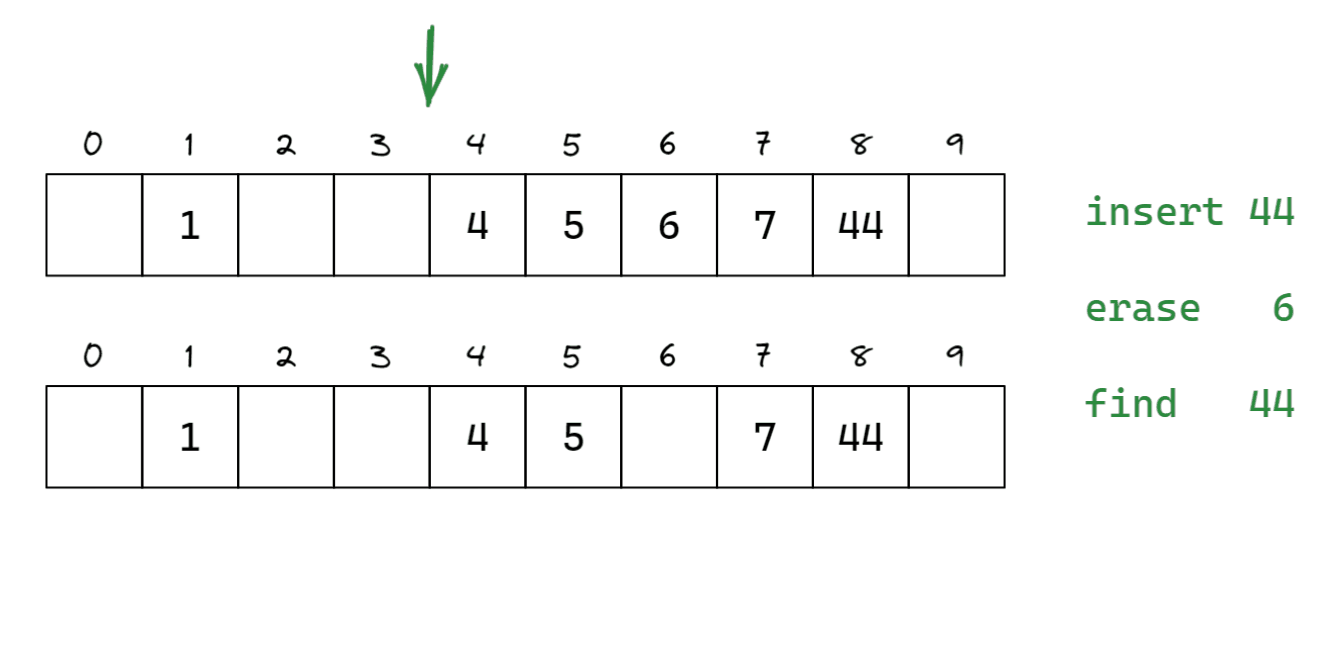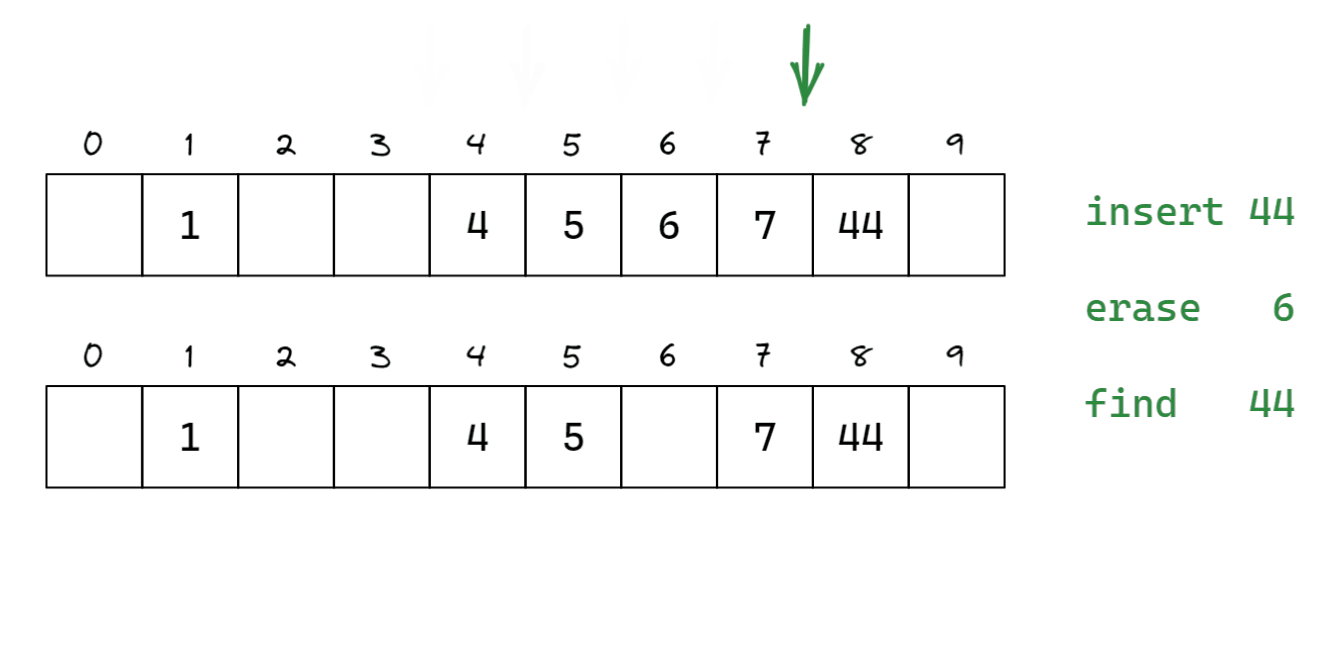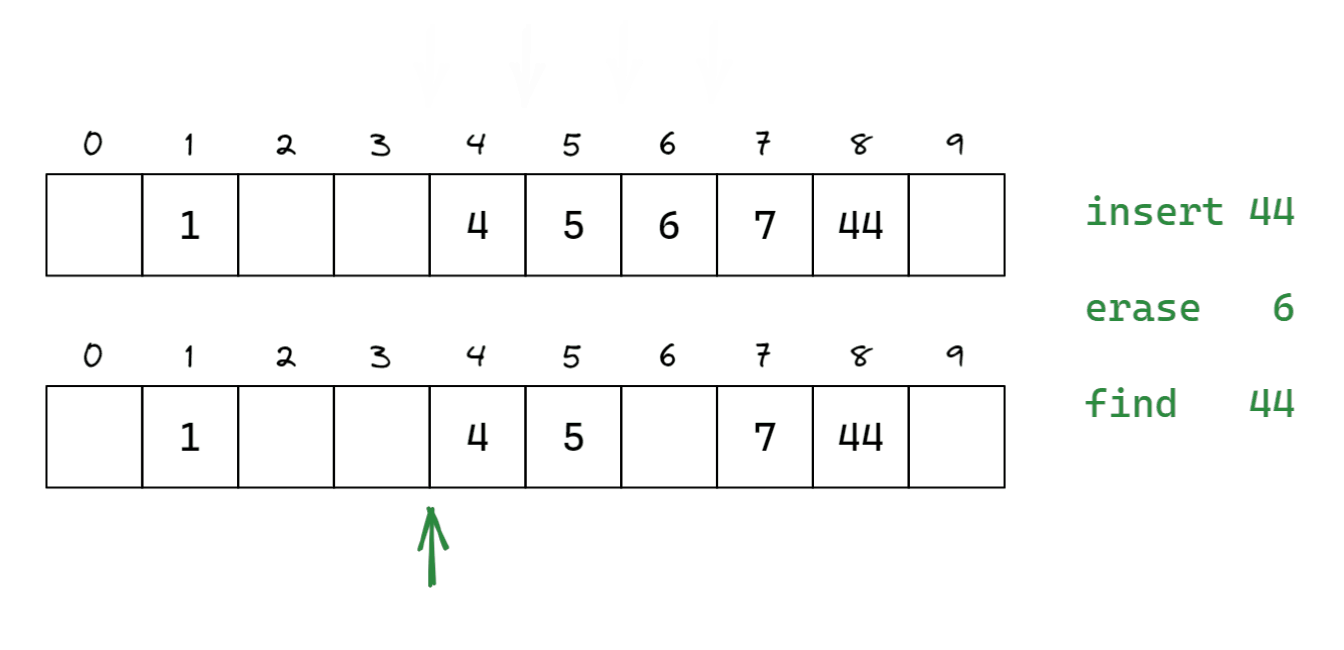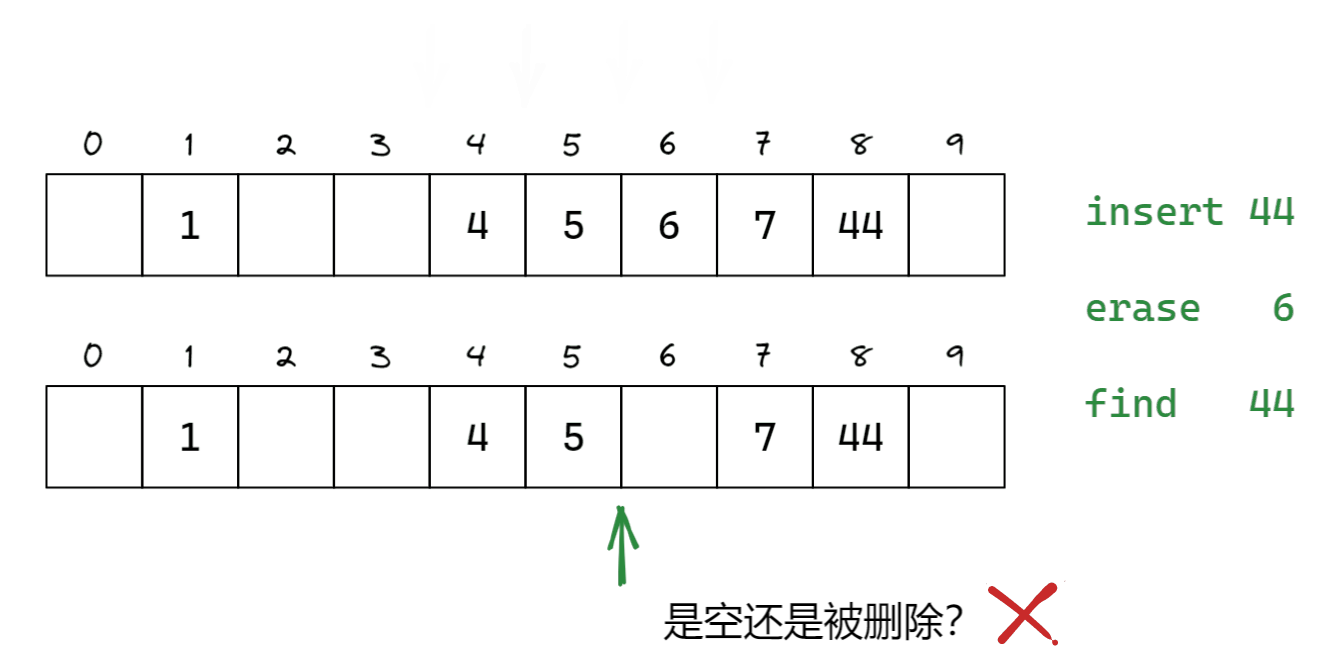
闭散列/开放定址法
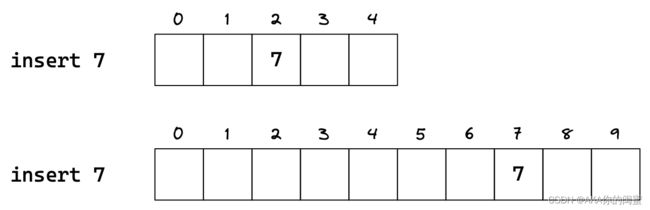
闭散列,又称开放定址法。当发生哈希冲突时,把元素放到冲突位置后的下一个空位中。
如何寻找空位呢?一般有线性探测和二次探测。如果没有空位,可以闭散列扩容。
两种探测方式
| 探测方式 | 解释 | 问题 |
|---|---|---|
| 线性探测 | 从冲突位置向后遇到的第一个空位,就是存放位置 | 连续位置冲突越来越多,引发洪水效应 |
| 二次探测 | 每次向后跳过 i 2 i^2 i2 个长度,如遇到空位就是存放位置 | 能缓解拥堵,快满时“绕圈”现象明显。 |
如何表示元素位置是否存在、为空、被删除?要为每个位置数据增加状态标记。
二次探测在得到位置后如果发生冲突,第一次向后跳过 1 2 1^2 12个长度、第二次 2 2 2^2 22个长度,如此类推,直到遇到空位置。
bool insert(const pair<K, V>& kv)
{
if (_table.size() == 0 || _size * 10 / _table.size() >= 7)
{
size_t new_size = _size == 0 ? 10 : _table.size() * 2;
hash_table<K, V> new_hash;
new_hash._table.resize(new_size);
for (auto& data : _table)
if (data._st == EXIST)
new_hash.insert(data._kv);
_table.swap(new_hash._table);
}
size_t hashi = kv.first % _table.size();
size_t i = 1;
size_t idx = hashi;
while (_table[idx]._st == EXIST)
{
if (_table[idx]._kv.first == kv.first)
return false;
idx += i; // 线性探测
idx += i * i; // 二次探测
idx %= _table.size();
}
_table[idx]._kv = kv;
_table[idx]._st = EXIST;
++_size;
return true;
}
闭散列扩容
当二次探测总是在正确位置“绕圈”时,只能用扩容解决问题。但什么时候该扩容呢?扩容多大呢?
载荷因子可以衡量哈希表的装载程度,它的定义是:
α = 表中元素个数 / 表的总长度 \alpha \; = \;表中元素个数\;/\;表的总长度 α=表中元素个数/表的总长度
负载因子越小,冲突概率越低,效率越高,但空间浪费就多。
使用闭散列时,荷载因子是决定哈希效率的重要因素,应严格限制在0.7-0.8以下。超过0.8,查表的缓存不命中率指数级上升。
哈希表的扩容要维护原有数据的存放位置。数据搬迁很麻烦,不如将原数据插入到新表。
bool insert(const pair<K, V>& kv)
{
if (_table.size() == 0 || _size * 10 / _table.size() >= 7)
{
size_t new_size = _size == 0 ? 10 : _table.size() * 2;
hash_table<K, V> new_hash;
new_hash._table.resize(new_size);
for (auto& data : _table)
{
if (data._st == EXIST)
new_hash.insert(data._kv);
}
_table.swap(new_hash._table);
}
// ...
}
HashNode<K, V>* Find(const K& key) {
if (_table.size() == 0)
return nullptr;
HashFunc hf;
size_t pos = hf(key) % _table.size();
size_t index = pos;
size_t i = 0;
while (_table[index]._status == EXIST) {
if (_table[index]._kv.first == key) {
return &_table[index];
}
++i;
index = pos + i;
index %= _table.size();
}
return nullptr;
}
bool Erase(const K& key) {
HashNode<K, V>* ret = Find(key);
if (ret == nullptr)
return false;
else {
ret->_status = EMPTY;
--_n;
return true;
}
}
开散列/拉链法/哈希桶
闭散列的线性探测和二次探测都会加剧哈希冲突,现实中几乎不会使用闭散列。
开散列又称拉链法、链地址法、开链法、哈希桶。
具有相同地址的key归于一个集合(桶),桶中元素通过链表链接起来,各链表的头结点存储在哈希表中。从根本上解决了冲突的问题。
template<class K, class V>
struct hash_node
{
pair<K, V> _kv;
hash_node<K, V>* _next;
hash_node<K, V>(const pair<K, V>& kv) : _kv(kv), _next(nullptr)
{}
};
template<class K, class V>
class hash_table
{
public:
typedef hash_node<K, V> node;
public:
~hash_table<K, V>() {
for (auto cur : _table) {
while (cur) {
node* next = cur->_next;
delete cur;
cur = next;
}
}
}
private:
vector<node*> _table;
size_t _size;
};
开散列实现
桶由链表实现,本质效率和线性探测一样。如果桶中节点过多会影响哈希表的性能。必须在适当条件下对哈希表增容。让哈希表处于最佳状态。
开散列的最佳情况是每个哈希桶中刚好挂一个节点。如果再插入必然会发生冲突。因此当元素个数等于桶的个数时,可以给哈希表增容。
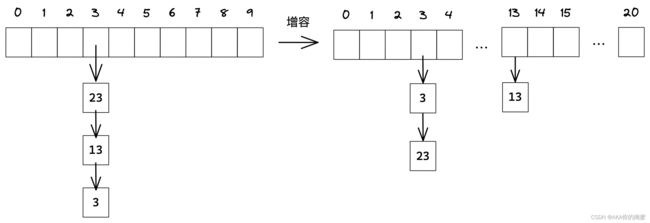
开散列扩容复用插入逻辑的话,会浪费原节点,最好是遍历原表节点放到新表中。
bool insert(const pair<K, V>& kv)
{
if (_table.empty() || _size == _table.size())
{
size_t new_size = _size == 0 ? 10 : _table.size() * 2;
vector<node*> new_table(new_size);
for (auto cur : _table)
{
while (cur)
{
size_t hashi = cur->_kv.first % _table.size();
node* next = cur->_next;
cur->_next = new_table[hashi];
new_table[hashi] = cur;
cur = next;
}
cur = nullptr;
}
_table.swap(new_table);
}
size_t hashi = kv.first % _table.size();
node* new_node = node(kv);
new_node->_next = _table[hashi];
_table[hashi] = new_node;
return true;
}
node* find(const K& key)
{
if (_table.empty())
return nullptr;
size_t hashi = key % _table.size();
node* cur = _table[hashi];
while (cur)
{
if (cur->_kv.first == key)
return cur;
cur = cur->_next;
}
return nullptr;
}
bool erase(const K& key)
{
if (_table.empty())
return false;
size_t hashi = key % _table.size();
node* cur = _table[hashi];
node* prev = nullptr;
while (cur)
{
if (cur->_kv.first == key)
{
if (!prev)
{
_table[hashi] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
3. 模拟实现
哈希表的实现比红黑树要简单不少,但是它的封装比较繁琐。
根据哈希表原理,实现unordered系列容器,需要对key类型作出如下要求:
| 参数 | 解释 |
|---|---|
Hash=hash |
支持取模或支持映射到整数进行取模 |
Pred=equal_to |
支持判断相等的函数 |
template < class Key, // unordered_map::key_type
class Value, // unordered_map::mapped_type
class Hash = hash<Key>, // unordered_map::hasher
class Pred = equal_to<Key>, // unordered_map::key_equal
class Alloc = allocator<pair<const Key,T>> // unordered_map::allocator_type
> class unordered_map;
3.1 改造哈希表
- unordered_map/unordered_set要复用同一个哈希表,同样要提供仿函数
KeyOfVal。 - 哈希只支持单向迭代器,所以只有++。
- 哈希表遍历是从头到尾遍历每个桶,必须能访问表中的数组,所以必须提供哈希表对象的指针。
template<class K, class V, class HashFunc, class KeyOfVal, class EqualKey>
class hash_table;
template<class K, class V, class HF, class KOV, class Ref, class Ptr>
struct __hash_iterator
{
typedef __hash_node<V> node;
typedef hash_table<K, V, HF, KOV> hash_table;
typedef __hash_iterator<K, V, HF, KOV, V&, V*> iterator;
typedef __hash_iterator<K, V, HF, KOV, Ref, Ptr> self;
node* _node;
const hash_table* _ht;
__hash_iterator(node* n, const hash_table* ht) : _node(n), _ht(ht)
{}
__hash_iterator(const iterator& it) : _node(it._node), _ht(it._ht)
{}
Ref operator*() { return _node->_val; }
Ptr operator->() { return &_node->_val; }
bool operator==(const self& s) { return _node == s._node; }
bool operator!=(const self& s) { return !this->operator==(s); }
self& operator++()
{
if (_node->_next)
{
_node = _node->_next;
}
else
{
size_t hashi = _ht->_hash(_ht->_kov(_node->_val)) % _ht->_table.size();
++hashi;
while (hashi < _ht->_table.size())
{
if (_ht->_table[hashi])
{
_node = _ht->_table[hashi];
break;
}
++hashi;
}
if (hashi == _ht->_table.size())
_node = nullptr;
}
return *this;
}
};
template<class V>
struct __hash_node
{
V _val;
__hash_node<V>* _next;
__hash_node<V>(const V& val) : _val(val), _next(nullptr)
{}
};
template<class K, class V, class HashFunc, class KeyOfVal>
class hash_table
{
public:
typedef __hash_node<V> node;
typedef __hash_iterator<K, V, HashFunc, KeyOfVal, V&, V*> iterator;
typedef __hash_iterator<K, V, HashFunc, KeyOfVal, const V&, const V*> const_iterator;
template<class K, class V, class HF, class KOV, class Ref, class Ptr>
friend struct __hash_iterator;
public:
const_iterator begin() const
{
for (auto cur : _table)
{
if (cur) return const_iterator(cur, this);
}
return end();
}
const_iterator end() const
{
return const_iterator(nullptr, this);
}
iterator begin()
{
for (auto cur : _table)
{
if (cur) return iterator(cur, this);
}
return end();
}
iterator end()
{
return iterator(nullptr, this);
}
public:
std::pair<iterator, bool> insert(const V& val)
{
auto pos = find(_kov(val));
if (pos != end())
return {pos, false};
if (_table.empty() || _table.size() == _size)
{
size_t new_size = _table.empty() ? 10 : _table.size() * 2;
std::vector<node*> new_table(new_size);
for (auto& cur : _table)
{
while (cur)
{
size_t hashi = _hash(_kov(cur->_val))%new_table.size();
node* next = cur->_next;
cur->_next = new_table[hashi];
new_table[hashi] = cur;
cur = next;
}
}
_table.swap(new_table);
}
size_t hashi = _hash(_kov(val)) % _table.size();
node* new_node = new node(val);
new_node->_next = _table[hashi];
_table[hashi] = new_node;
++_size;
return {iterator(new_node, this), true};
}
iterator find(const K& key)
{
if (_table.empty())
return end();
size_t hashi = _hash(key) % _table.size();
node* cur = _table[hashi];
while (cur)
{
if (_hash(_kov(cur->_val)) == _hash(key))
return iterator(cur, this);
cur = cur->_next;
}
return end();
}
bool erase(const K& key)
{
if (_table.empty())
return false;
size_t hashi = _hash(key) % _table.size();
node* cur = _table[hashi];
node* prev = nullptr;
while (cur)
{
if (_hash(_kov(cur->_val)) == _hash(key))
{
if (!prev)
{
_table[hashi] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
private:
std::vector<node*> _table;
size_t _size = 0;
KeyOfVal _kov;
HashFunc _hash;
};
3.2 封装容器
unordered_set
template<class K, class Hash = hash<K>>
class unordered_set
{
private:
struct KeyOfVal {
const K& operator()(const K& key) const { return key; }
};
public:
typedef hash_table<K, K, Hash, KeyOfVal> rep_type;
typedef typename rep_type::const_iterator iterator;
typedef typename rep_type::const_iterator const_iterator;
public:
std::pair<iterator, bool> insert(const K& key) { return _ht.insert(key); }
size_t erase(const K& key) { return _ht.erase(key); }
iterator find(const K& key) { return _ht.find(key); }
iterator begin() { return _ht.begin(); }
iterator end() { return _ht.end(); }
const_iterator begin() const { return _ht.begin(); }
const_iterator end() const { return _ht.end(); }
private:
rep_type _ht;
};
unordered_map
template<class K, class V, class Hash = hash<K>>
class unordered_map
{
private:
struct KeyOfVal {
const K& operator()(const std::pair<const K, V>& kv) const {
return kv.first;
}
};
public:
typedef hash_table<K, std::pair<const K, V>, Hash, KeyOfVal> rep_type;
typedef typename rep_type::iterator iterator;
typedef typename rep_type::const_iterator const_iterator;
public:
std::pair<iterator, bool> insert(const std::pair<K, V>& kv) { return _ht.insert(kv); }
size_t erase(const K& key) { return _ht.erase(key); }
iterator find(const K& key) { return _ht.find(key); }
iterator begin() { return _ht.begin(); }
iterator end() { return _ht.end(); }
const_iterator begin() const { return _ht.begin(); }
const_iterator end() const { return _ht.end(); }
V& operator[](const K& key) { return _ht.insert({key, V()}).first->second; }
private:
rep_type _ht;
};
4. 哈希应用
4.1 位图
哈希是存在一定空间消耗的,在处理海量数据的情况下可以选择位图。
位图的定义
位图用一段空间的每个比特位:
- 比特位的位置映射到特定的元素;
- 比特位的值即01来表示二元状态。
位图可以记录某个元素的某个二元状态,通常用于处理海量数据,且数据无重复的场景。通常是用来判断某个数据存不存在。
位图的大小和数据量无关,而是和数据最大值有关。整型最大能表示42亿多。故位图最大为 500 M B 500MB 500MB。
位图的优劣
- 位图的查找速度快。节省空间。
- 但位图只能处理整数,只能记录二元状态。
位图的实现
位图就是将元素以绝对映射的方式到下标位置。
以一个字节八个比特位为一组, x / 8 x/8 x/8 得元素在第几个组,然后 x % 8 x\%8 x%8 得元素在组中第几个比特位。
template <size_t N>
class bit_set
{
public:
bit_set() { _bits.resize(N / 8 + 1); }
void set(size_t x)
{
int i = x / 8; // 字节位
int j = x % 8; // 比特位
_bit[i] |= (1 << j); // 比特位置1
}
void reset(size_t x)
{
int i = x / 8;
int j = x % 8;
_bit[i] &= ~(1 << j) // 比特位置0
}
bool test(size_t x)
{
int i = x / 8;
int j = x % 8;
return _bit[i] & (1 << j); // 探测该比特位
}
private:
vector<char> _bits;
};
整数相除会丢弃余数,所以加一个字节保证空间大小一定满足要求。
//开满大小的位图
bitset<(size_t)-1> bs1;
bitset<0xffffffff> bs2;
位图的应用
问题一
给定40亿个整数,设计算法找到只出现一次的整数?
找到只出现一次的整数,需要两个位图,一个保存这些数的是否出现一次,一个保存是否出现。
template <size_t N>
void handlequestion2(vector<int>& in, vector<int>& out)
{
bitset<N> bs1;
bitset<N> bs2;
for (auto e : in) {
if (!_bs2.test(x)) {
_bs1.set(x);
_bs2.set(x);
}
else {
_bs1.reset(x);
}
}
for (int i = 0; i < N; i++)
if (_bs1.test(i))
v.push_back(i);
}
问题二
给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
思路一:将第一个文件中的整数set到位图中,再遍历第二个文件的整数test该位图,如果已经存在则属于交集,输出后再将其reset防止重复。
template <size_t N>
void handlequestion2(vector<int>& in1, vector<int>& in2, vector<int>* out)
{
bitset<N> bs;
for (auto e : in1) {
bs.set(e);
}
for (auto e : in2) {
if (bs.test(e)) {
bs.reset(e);
out->push_back(e);
}
}
}
思路二:两个文件分别set到两个位图,取两个位图相与后的结果,就是交集。
template <size_t N>
void handlequestion2(vector<int>& in1, vector<int>& in2, vector<int>* out)
{
bitset<N> bs1;
bitset<N> bs2;
for (auto e : in1) bs1.set(e);
for (auto e : in2) bs2.set(e);
for (int i = 0; i < N; i++) {
if (bs1.test(i) && bs2.test(i))
out->push_back(i);
}
}
问题三
100亿个整数,1G内存,找到出现不超过2次的整数。
两个位图可表示4种状态,可以描述出现0次,出现1次,出现2次,2次以上。
template <size_t N>
void handlequestion3(vector<int>& in, vector<int>* out)
{
bitset<N> bs1;
bitset<N> bs2;
if(bs1.test(x) == false && bs2.test(x) == false) // 00 -> 01
{
bs1.set(x);
}
else if (bs1.test(x) == true && bs2.test(x) === false) // 01 -> 10
{
bs1.reset(x);
bs2.set(x);
}
else if (bs1.test(x) == false && bs2.test(x) === true) // 10 -> 11
{
bs1.set(x);
bs2.set(x);
}
for (int i = 0; i < N; i++) {
if ((_bs1.test(i) && !_bs2.test(i)) || (!_bs1.test(i) && _bs2.test(i)))
v->push_back(i);
}
}
4.2 布隆过滤器
位图只能处理整数,布隆过滤器可以处理任意类型。
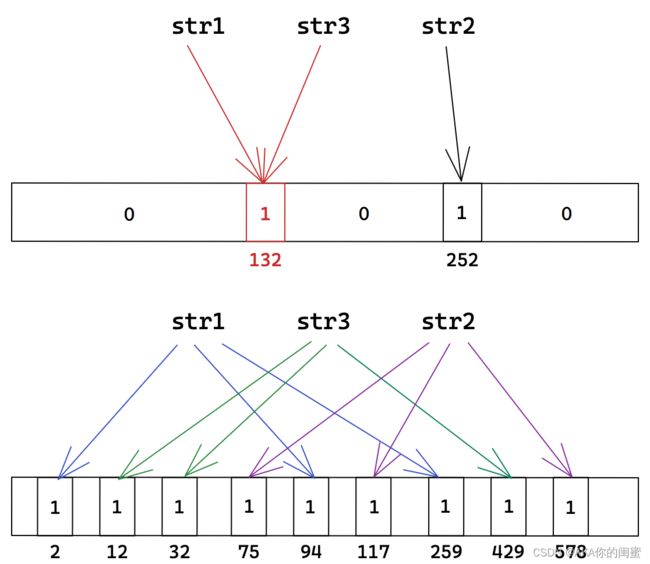
布隆过滤器的定义
有些类型虽不可直接映射,但可以通过哈希函数转整数间接映射。可以认为,布隆过滤器就是加上哈希函数的位图。
但使用哈希函数就不可避免会发生哈希冲突。发生冲突会导致误判,将一个不存在的元素误判为存在。
解决冲突的方式:
- 使用更大空间,自然会减少冲突的概率。
- 多副本映射,使用多个哈希函数,将同一元素映射在不同位置上,降低误判的概率。
倘若某个元素的位置都被其他元素映射了,那它就会被误判存在。也就是说,结果存在不一定对,结果不存在一定对。所以尽量使用布隆过滤器判断“不在”。
布隆过滤器的优劣
| 优点 | 解释 |
|---|---|
| 查询效率高 | O ( K ) O(K) O(K),K是映射副本的个数,属于常数次。 |
| 占存小,保密性高 | 不存储元素本身,只存储映射状态。 |
| 缺点 | 解释 |
| 有误判率 | 不能准确判断元素是否存在。 |
| 不能删除 | 如果采用计数方式删除,可能会存在计数回绕问题。 |
布隆过滤器的实现
布隆过滤器
模版参数N表示需要映射的元素个数,但防止冲突一个元素需要多个比特位,那具体要开辟多大空间呢?
布隆过滤器大小 = 4.3 ∗ 映射的元素个数 布隆过滤器大小=4.3*映射的元素个数 布隆过滤器大小=4.3∗映射的元素个数
#pragma once
#include 布隆过滤器的应用
如何使布隆过滤器支持删除?
布隆过滤器本身不支持删除。因为在发生冲突的情况下将比特位置0,可能会导致误判不在。
利用多个位图,每个元素占有多个比特位,存储引用计数。会导致耗费空间变多,布隆过滤器优势减弱。
4.3 哈希切分
应用一
给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?
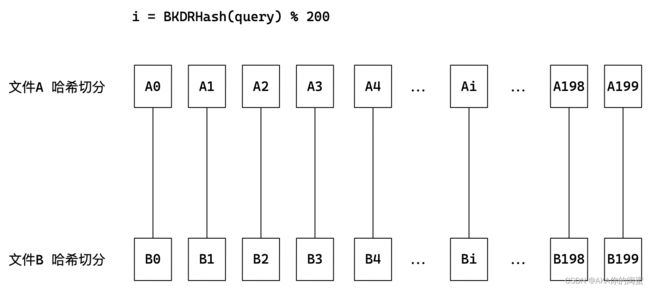
先将文件A和文件B分别各切分成200个小文件。
利用哈希函数,算出每个query的映射位置,是多少就放进多少号文件。比如文件A中的某个query的哈希结果是3,就放到A3号文件中,B中的query也同理。
因为文件A和文件B用同一个哈希函数,所以两个文件中相同的query一定进入了同一个编号的小文件中。所以只要对比编号相同的哈希桶是否存在相同的元素即可。
小文件就相当于是一个哈希桶,相同哈希结果的query会到同一个桶中。
如果 A i A_i Ai和 B i B_i Bi两个桶太大,超过内存限制,可以换一个哈希算法,再对这两个桶切分一次。
应用二
给一个超过100G大小的日志文件存着IP地址,我们只有1G内存,设计算法找到出现次数TopK的IP地址?
遍历文件读取IP,i=BKDR(ip)%100下标为多少,IP就进入编号为多少的文件。
通过哈希算法一定会将相同的IP进入同一个文件,所以统计该文件内各IP的次数就是该IP的出现次数。
一致性哈希
哈希与加密