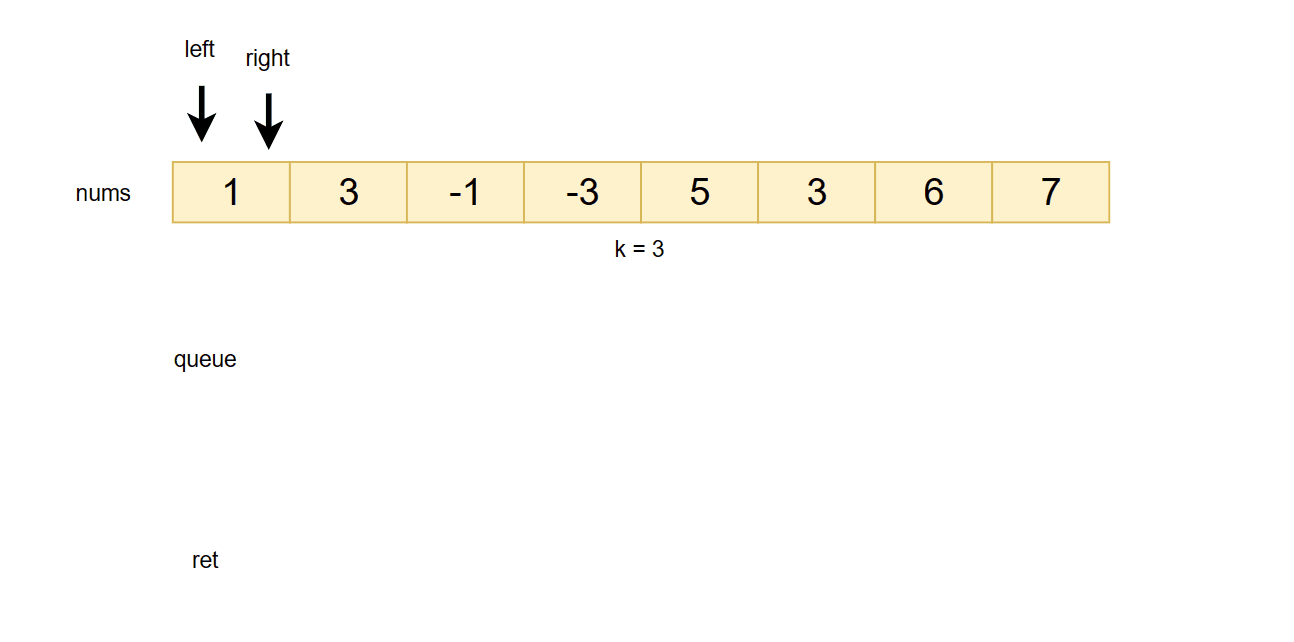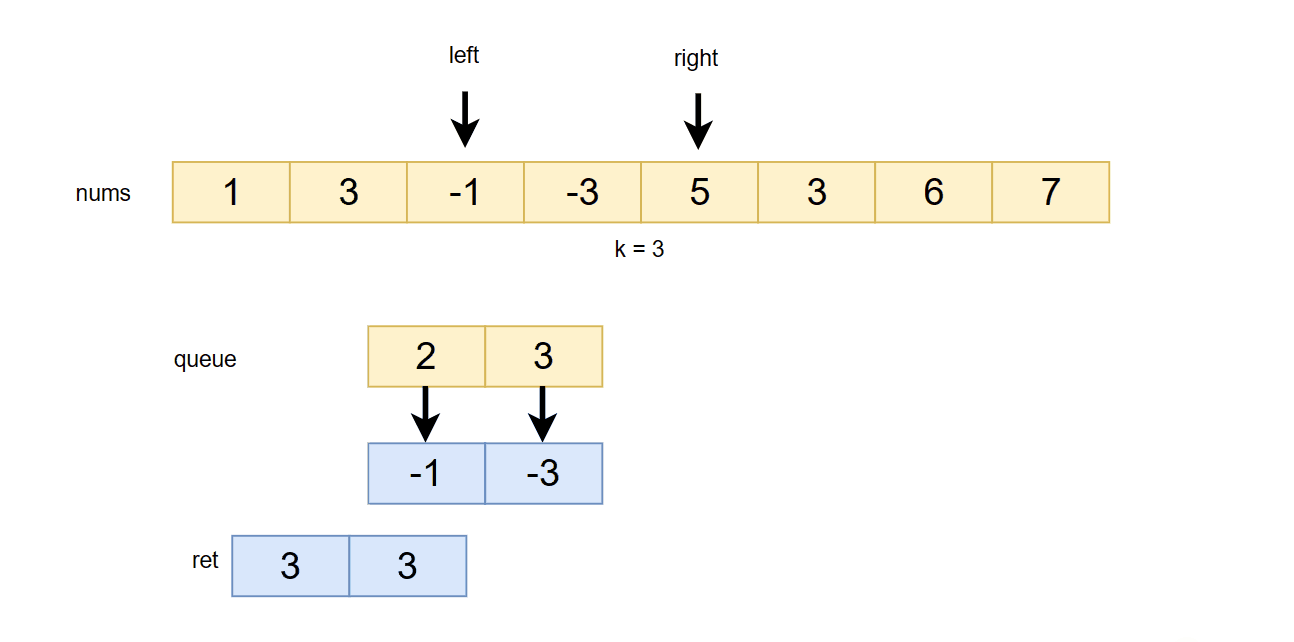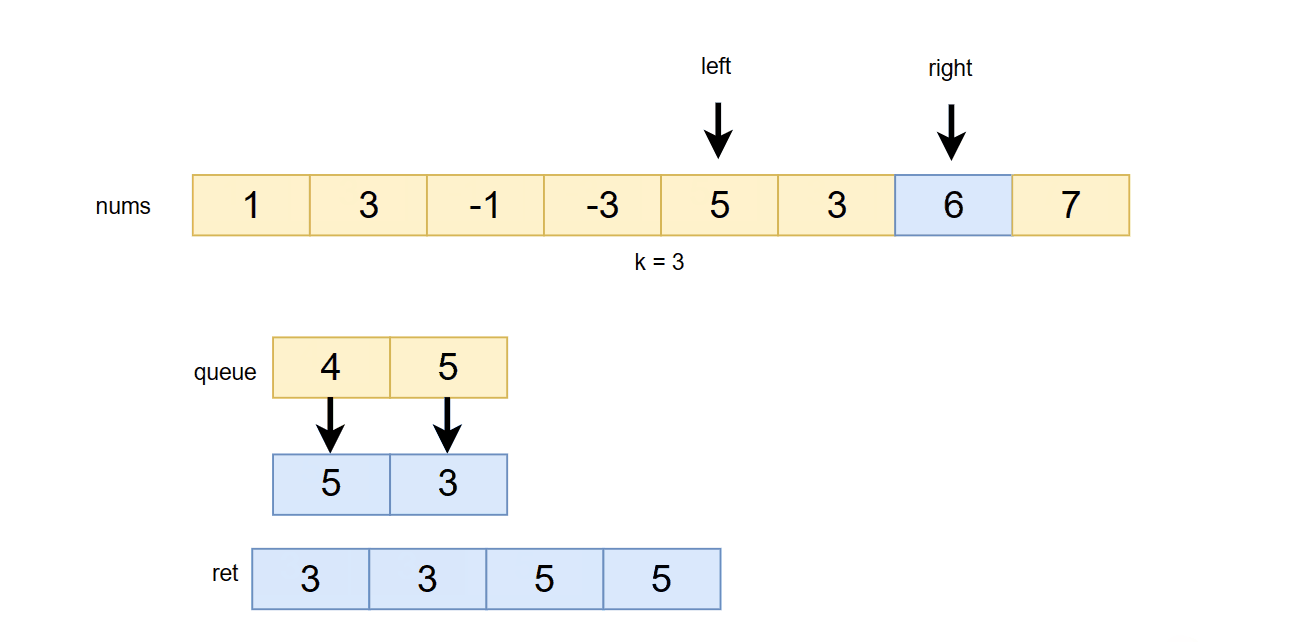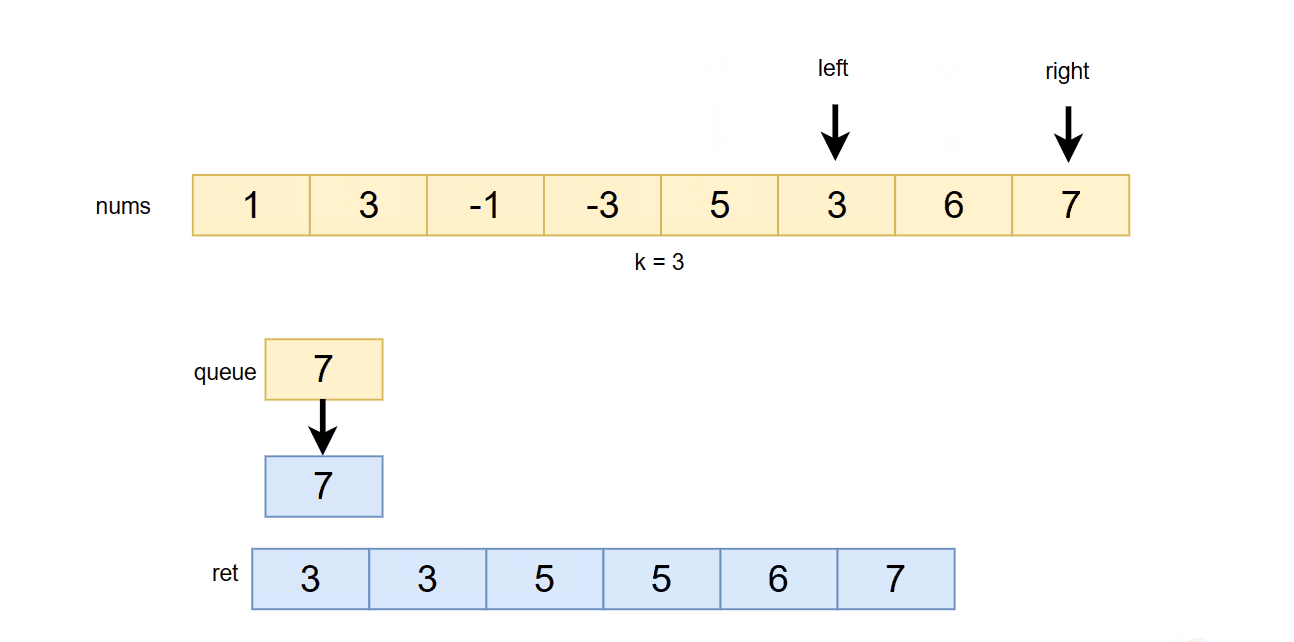滑动窗口的最大值&&最小值

        欢迎来到小林的博客！！
      ️博客主页：✈️林 子
      ️博客专栏：✈️ 小林的算法笔记
      ️社区 :✈️ 进步学堂
      ️欢迎关注：点赞收藏✍️留言

滑动窗口的最大值

题目摘自leetcode，链接：239. 滑动窗口最大值 - 力扣（LeetCode）

难度：困难

题目描述:

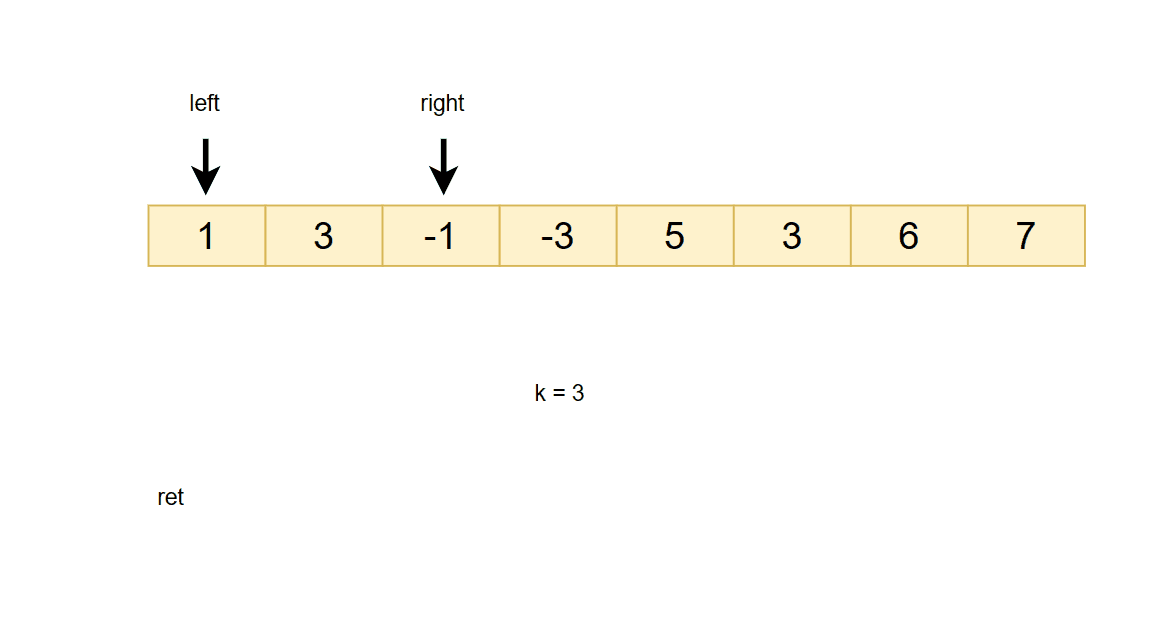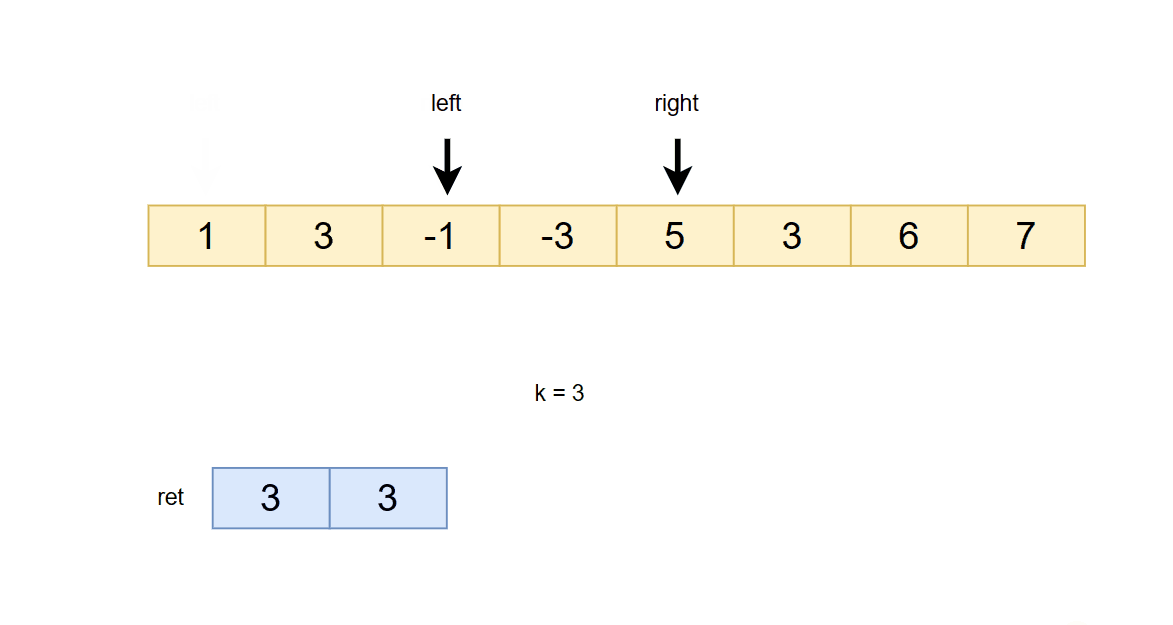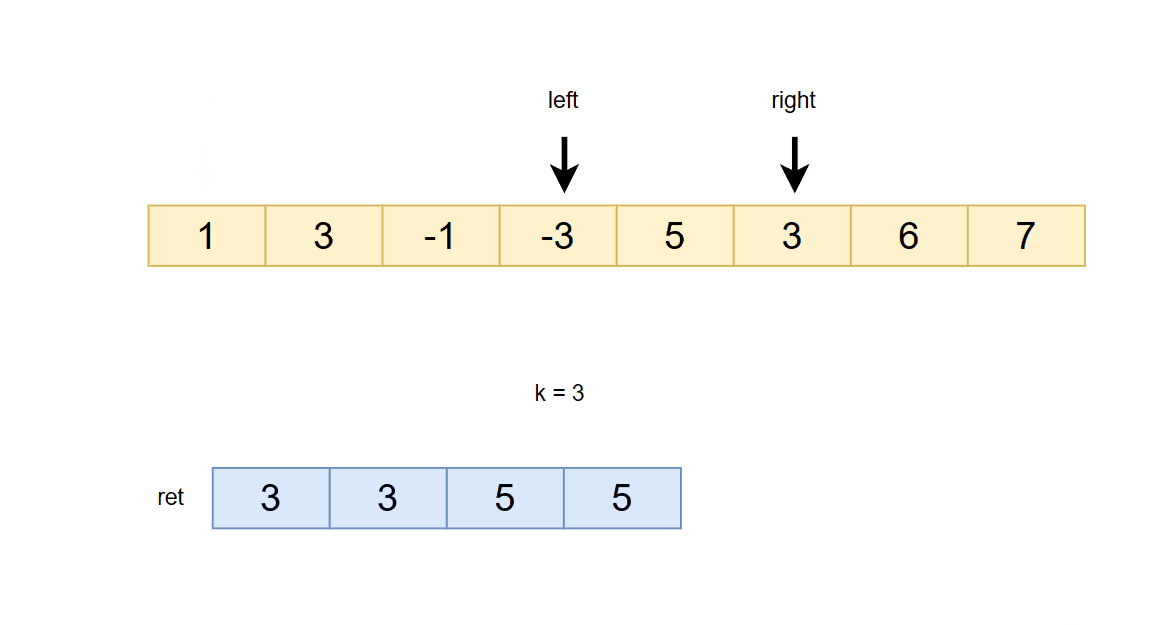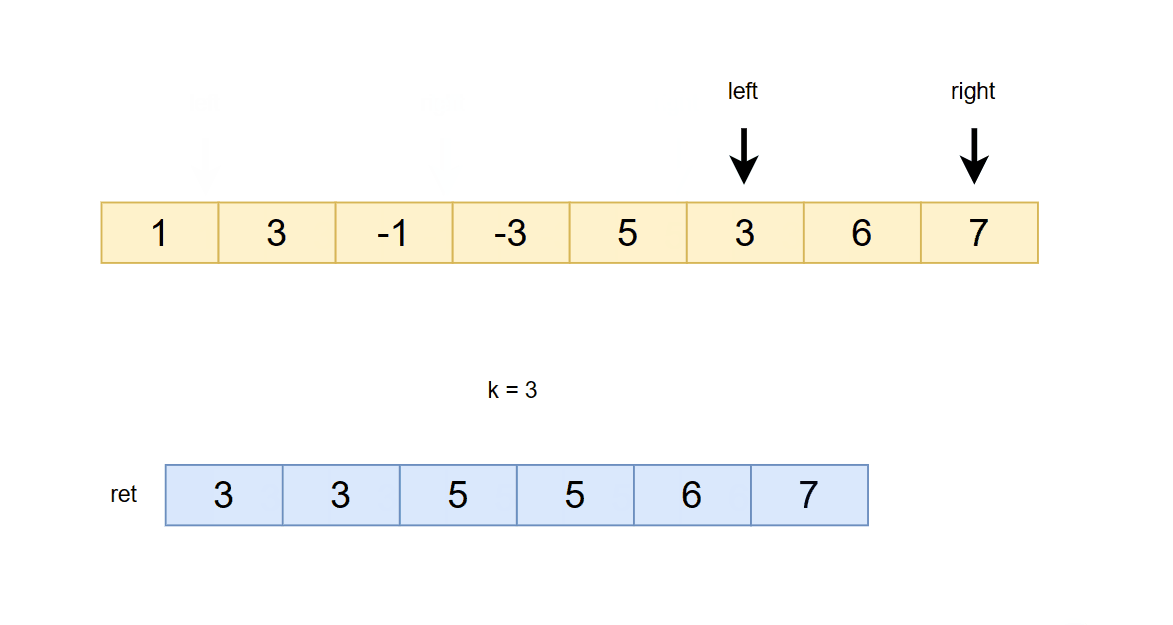
给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2 ：

输入：nums = [1], k = 1
输出：[1]

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104
• 1 <= k <= nums.length

看到这题时，我的第一反应就是双指针暴力解法，用双指针固定住两边的值，随后每次遍历一遍求得最大值。

但是后面发现超时了，这是因为给的数值范围最大是10万。 而暴力每次循环的复杂度为 O (N - K) * K ，当K为5W，N为10W时，那么复杂度就会变成5W * 5W 。所以就会超时。 而我们可以用队列来优化。

注意！

该队列必须支持尾删功能，我们可以用数组自己模拟一个队列出来。每次往队列插入数据前先检查right指针的数据是否大于队尾元素，如果大于就移除掉队尾元素。还有一个问题就是队列的队头元素所在的下标如果不在滑动窗口内了，那么也要把该元素移除。所以这也就意味着我们的队列必须存储对应数据的下标！！否则无法判断队头元素是否还在滑动窗口内。而当滑动窗口的长度大于等于k时，我们再把数据放进ret数组中。

所以我们主要是分为以下几个步骤：

1. 判断队头数据是否在滑动窗口内，用left 和 队头存储的下标做比较

2. 用right下标对应的数据和队尾存储下标对应的数据做比较，如果小于就移除队尾数据，一直循环，直到队列为空或者队尾数据大于right下标指向的数据

3. 往队尾push right指向的数据

**4. 如果right - left 长度 >= k -1 ，则把队头的数据加入到返回的数组中 **

5. 移动right和left指针，如果right - left < k -1 ， 则不移动left。

代码：

vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> ret; //返回的数组
        vector<int> queue(nums.size()); //模拟的队列
        int hh = 0 , tt = 0; //队头和队尾，tt指向下一个插入的位置，真正的队尾是tt-1
        int left = 0 ,right = 0; //2个指针固定滑动窗口
        while(right < nums.size()) //right 到达 nums.size() -1，说明滑动窗口到达了边界
        {
            //1. hh < tt 意思队列不为空，left > queue[hh] 说明队头不在滑动窗口内
            while(hh < tt && left > queue[hh]) hh++; //pop掉队头元素
            //2. 如果right指向的元素大于队尾下标指向的元素，那么pop掉队尾,tt指向的是下一个插入位置的值，所以tt - 1 才是队尾
            while(hh < tt && nums[queue[tt - 1]] <= nums[right]) tt--;
            //3. 把right入队
            queue[tt++] = right;  
            //4. 判断窗口大小
            if(right - left >= k - 1)
            {
                //滑动窗口大小正常，把队头指向的值push给right
                ret.push_back(nums[queue[hh]]); 
                //5.移动滑动窗口
                left++ , right++;
            }else right++; //5. 大小不满足只移动right
        } 
        return ret;
    }

运行结果：

滑动窗口最小值

而滑动窗口的最小值也是一样的，我们只需要让队尾元素大于right下标指向的元素，就进行尾删即可。也就是把上面代码中的while(hh < tt && nums[queue[tt - 1]] <= nums[right]) tt--; 替换成 while(hh < tt && nums[queue[tt - 1]] > nums[right]) tt--;

滑动窗口最小值的完整代码则是：

vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> ret; //返回的数组
        vector<int> queue(nums.size()); //模拟的队列
        int hh = 0 , tt = 0; //队头和队尾，tt指向下一个插入的位置，真正的队尾是tt-1
        int left = 0 ,right = 0; //2个指针固定滑动窗口
        while(right < nums.size()) //right 到达 nums.size() -1，说明滑动窗口到达了边界
        {
            //1. hh < tt 意思队列不为空，left > queue[hh] 说明队头不在滑动窗口内
            while(hh < tt && left > queue[hh]) hh++; //pop掉队头元素
            //2. 如果right指向的元素小于队尾下标指向的元素，那么pop掉队尾,tt指向的是下一个插入位置的值，所以tt - 1 才是队尾
            while(hh < tt && nums[queue[tt - 1]] > nums[right]) tt--;
            //3. 把right入队
            queue[tt++] = right;  
            //4. 判断窗口大小
            if(right - left >= k - 1)
            {
                //滑动窗口大小正常，把队头指向的值push给right
                ret.push_back(nums[queue[hh]]); 
                //5.移动滑动窗口
                left++ , right++;
            }else right++; //5. 大小不满足只移动right
        } 
        return ret;
    }

运行结果：