FPGA实现Cordic算法——向量模式
FPGA实现Cordic算法——向量模式
- FPGA实现Cordic算法——向量模式
-
- 1.cordic算法基本原理
- 2.FPGA实现cordic算法向量模式
-
- i、FPGA串行实现cordic
- ii、FPGA流水线实现cordic
- iii、实验结果
FPGA实现Cordic算法——向量模式
1.cordic算法基本原理
FPGA中运算三角函数,浮点数的能力有限,而cordic算法能够将三角函数运算转换为简单的移位和加减法进行迭代得到近似结果,能够有效降低运算代价,提升运算效率。
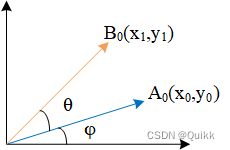
如上图所示,若已知点矢量终点A 0 _0 0 (x 0 _0 0,y 0 _0 0) ,若将该矢量逆时针旋转 θ \theta θ 可以根据三角运算得到B 0 _0 0 (x 1 _1 1,y 1 _1 1)点坐标:
{ x 0 = l ∗ c o s ψ y 0 = l ∗ s i n ψ { x 1 = l ∗ c o s ( θ + ψ ) = l ∗ ( c o s θ c o s ψ − s i n θ s i n ψ ) = x 0 c o s θ − y 0 s i n θ y 1 = l ∗ s i n ( θ + ψ ) = l ∗ ( s i n θ c o s ψ + c o s θ s i n ψ ) = x 0 s i n θ + y 0 c o s θ \begin{cases} x_0 = l*cos\psi \\ y_0 = l*sin\psi \\ \end{cases} \\ \begin{cases} x_1 = l*cos(\theta+\psi)=l*(cos\theta cos\psi -sin\theta sin\psi) = x_0 cos\theta - y_0 sin\theta\\ y_1 = l*sin(\theta+\psi)=l*(sin\theta cos\psi +cos\theta sin\psi) = x_0 sin\theta + y_0 cos\theta\\ \end{cases} {x0=l∗cosψy0=l∗sinψ{x1=l∗cos(θ+ψ)=l∗(cosθcosψ−sinθsinψ)=x0cosθ−y0sinθy1=l∗sin(θ+ψ)=l∗(sinθcosψ+cosθsinψ)=x0sinθ+y0cosθ
令 θ 1 = − θ \theta_1 = -\theta θ1=−θ,即顺时针旋转 θ \theta θ 角度,则:
{ x 0 c o s θ 1 − y 0 s i n θ 1 = x 0 c o s θ + y 0 s i n θ x 0 s i n θ 1 + y 0 c o s θ 1 = y 0 c o s θ − x 0 s i n θ \\ \begin{cases} x_0 cos\theta_1 - y_0 sin\theta_1 = x_0 cos\theta + y_0 sin\theta \\ x_0 sin\theta_1 + y_0 cos\theta_1 = y_0 cos\theta - x_0 sin\theta \\ \end{cases} {x0cosθ1−y0sinθ1=x0cosθ+y0sinθx0sinθ1+y0cosθ1=y0cosθ−x0sinθ
联立上述两个式子,引入常数$ d (d=-1,+1)$ ,因此可得:
{ x 0 c o s θ − d y 0 s i n θ = c o s θ ( x 0 − d y 0 t a n θ ) y 0 c o s θ + d x 0 s i n θ = c o s θ ( y 0 + d x 0 t a n θ ) \\ \begin{cases} x_0 cos\theta - dy_0 sin\theta = cos\theta(x_0 - dy_0 tan\theta) \\ y_0 cos\theta + dx_0 sin\theta = cos\theta(y_0 + dx_0 tan\theta) \\ \end{cases} {x0cosθ−dy0sinθ=cosθ(x0−dy0tanθ)y0cosθ+dx0sinθ=cosθ(y0+dx0tanθ)
这个算法的核心在于将一系列已知的 t a n θ tan\theta tanθ作为表格键值进行存储,而 t a n θ tan\theta tanθ可以约等于 1 2 n \frac{1}{2^n} 2n1并且。 1 2 n \frac{1}{2^n} 2n1在FPGA中可以通过右移进行快速运算。 t a n θ tan\theta tanθ各个已知存储值如下:
| i i i | θ \theta θ | t a n θ tan\theta tanθ | c o s θ cos\theta cosθ | ∏ c o s θ \prod cos\theta ∏cosθ |
|---|---|---|---|---|
| 0 | 45 | 1 | 0.707106781186548 | 0.707106781186548 |
| 1 | 25.56505 | 0.50 | 0.894427190999916 | 0.632455532033676 |
| 2 | 14.03243 | 0.25 | 0.970142500145332 | 0.613571991077897 |
| 3 | 7.125016 | 0.125000000000000 | 0.992277876713668 | 0.608833912517753 |
| 4 | 3.576334 | 0.0625000000000000 | 0.998052578482889 | 0.607648256256168 |
| 5 | 1.789910 | 0.0312500000000000 | 0.999512076087079 | 0.607351770141296 |
| 6 | 0.895173 | 0.0156250000000000 | 0.999877952034695 | 0.607277644093526 |
| 7 | 0.447614 | 0.00781250000000000 | 0.999969483818788 | 0.607259112298893 |
| 8 | 0.223810 | 0.00390625000000000 | 0.999992370692779 | 0.607254479332563 |
| 9 | 0.111905 | 0.00195312500000000 | 0.999998092656824 | 0.607253321089875 |
| 10 | 0.055952 | 0.000976562500000000 | 0.999999523163183 | 0.607253031529135 |
| 11 | 0.027976 | 0.000488281250000000 | 0.999999880790732 | 0.607252959138945 |
| 12 | 0.013988 | 0.000244140625000000 | 0.999999970197679 | 0.607252941041397 |
| 13 | 0.006994 | 0.000122070312500000 | 0.999999992549420 | 0.607252936517011 |
| 14 | 0.003497 | 6.10351562500000e-05 | 0.999999998137355 | 0.607252935385914 |
| 15 | 0.001748 | 3.05175781250000e-05 | 0.999999999534339 | 0.607252935103140 |
而多次旋转过程中,每次旋转的 c o s θ cos\theta cosθ需要连续相乘,而多次相乘极限也趋近与0.607252这一个常数,因此也可做近似处理。那么现在还有最后一个问题,这一系列角度能够通过多次旋转得到任意的角度吗?可以看到每个角度是不断降低减半的,呈递减的分布,从宏观上观察大致是可以进行趋近到某一个常数的。
cordic算法有两个模式:
1)向量模式,已知点坐标(x0,y0),可以求得该向量的角度即arctan(y0/x0)。这种可以理解为需要通过多次旋转,将该向量旋转至x轴上,即y0 = 0,此时旋转过的角度即为向量角度,x最终坐标即为向量的长度。
2)旋转模式,已知角度 θ \theta θ ,求 s i n θ sin\theta sinθ及 c o s θ cos\theta cosθ
{ x 0 c o s θ − d y 0 s i n θ = c o s θ ( x 0 − d y 0 t a n θ ) y 0 c o s θ + d x 0 s i n θ = c o s θ ( y 0 + d x 0 t a n θ ) \\ \begin{cases} x_0 cos\theta - dy_0 sin\theta = cos\theta(x_0 - dy_0 tan\theta) \\ y_0 cos\theta + dx_0 sin\theta = cos\theta(y_0 + dx_0 tan\theta) \\ \end{cases} {x0cosθ−dy0sinθ=cosθ(x0−dy0tanθ)y0cosθ+dx0sinθ=cosθ(y0+dx0tanθ)
令y0 = 0
{ c o s θ ( x 0 − d y 0 t a n θ ) = c o s θ x 0 c o s θ ( y 0 + d x 0 t a n θ ) = s i n θ y 0 \begin{cases} cos\theta(x_0 - dy_0 tan\theta) = cos\theta x_0\\ cos\theta(y_0 + dx_0 tan\theta) = sin\theta y_0\\ \end{cases} {cosθ(x0−dy0tanθ)=cosθx0cosθ(y0+dx0tanθ)=sinθy0
什么意思呢,类似当前有个单位圆,初始点在A(x,0)这一点,经过旋转多次可以得到B(x1,y1)。此时
{ x 1 = c o s ( θ ) y 1 = s i n ( θ ) \begin{cases} x_1 = cos(\theta)\\ y_1 = sin(\theta) \end{cases} {x1=cos(θ)y1=sin(θ)
但是因为这个旋转变换是伪旋转变换,需要乘以一个 c o s θ cos\theta cosθ的系数。
2.FPGA实现cordic算法向量模式
这里以向量模式为例子进行FPGA实现,首先构建matlab仿真程序
function [len,theta] = cordic_theat(x_in,y_in)
clc;
clear x y z;
z_ref=[ 45,...
26.56505113840103,...
14.036243438720703,...
7.1250163316726685,...
3.5763343572616577,...
1.7899105548858643,...
0.8951736688613892,...
0.4476141333580017,...
0.22381049394607544,...
0.11190563440322876,...
0.05595284700393677,...
0.027976393699645996,...
0.013988196849822998,...
0.006994098424911499,...
0.0034970492124557495,...
0.00174852460622787475].*2^(24);
times = 16;%迭代次数
x = zeros(times+1,1);
y = zeros(times+1,1);
z = zeros(times+1,1);
d = 1;
y(1,1) = abs(y_in)*2^(12);
x(1,1) = abs(x_in)*2^(12);
z(1,1) = 0;
for i = 1: times
if( y(i,1) < 0 )
% d = 1;
x(i+1,1) = x(i,1) - d/2^(i-1)*y(i,1);
y(i+1,1) = y(i,1) + d/2^(i-1)*x(i,1);
z(i+1,1) = z(i,1) - d*( z_ref(i) );
else
% d = -1;
x(i+1,1) = x(i,1) + d/2^(i-1)*y(i,1);
y(i+1,1) = y(i,1) - d/2^(i-1)*x(i,1);
z(i+1,1) = z(i,1) + d*( z_ref(i) );
end
end
my_z = z(times+1,1)/2^(24);
my_x = x(times+1,1)/2^(12) * 0.607253;
len = my_x;
if( x_in >= 0 && y_in>=0)
theta = my_z;
elseif (x_in <= 0 && y_in >=0)
theta = 180 - my_z;
elseif (x_in <= 0 && y_in <=0)
theta = 180 + my_z;
elseif (x_in>= 0 && y_in<= 0)
theta = 360 - my_z;
end
end
实际值比对程序:
t = 0:0.01:2*pi;
x=cos(t);
y=sin(t);
len = zeros( 1,length(t));
theta = zeros(1,length(t));
for i = 1:length(t)
[len(i),theta(i)] = cordic_theat( x(i),y(i) );
end
plot( abs(theta-t/pi*180) );
axis([0 640 -0.5e-3 2e-3]);
运行结果显示,与真实值相比16次迭代基本上可以满足使用需要
i、FPGA串行实现cordic
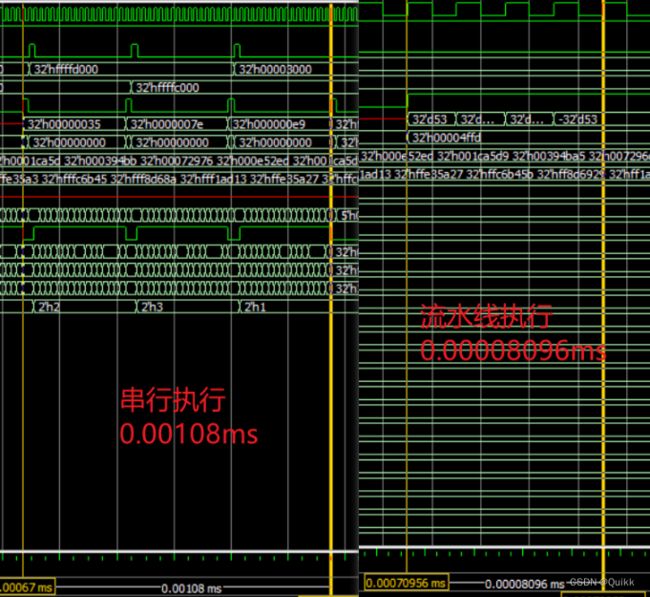
FPGA流水线实现和串行实现,大概的区别是。假如工厂需要加工一个零件,这个零件需要六个步骤完成,每个步骤10s,每个步骤不能同时进行[步骤前后有先后关系]。如果是串行,是一个工人完成六道工序,也就是每60s加工完成一个零件,然后取新的物料进行完成。而流水线实现是安排六个人,每个人只完成一道工序,也就是正常运行过程中,每10s就能取一次物料。从吞吐率来说,串行每60s取一次数据而流水线每10s便能取一次数据,相应的输出也会更加快。串行速度慢,但消耗人工少;流水线速度快但,消耗六倍人工,这是FPGA中典型的空间换取时间的例子。
实现代码如下:
module cordic_serial(
input sys_clk,
input sys_rst_n,
input user_data_valid,
input [31:0] user_x,
input [31:0] user_y,
output reg user_data_out_valid,
output reg [31:0] user_theat,
output [31:0] user_len
);
//输入为有符号数(定点数) 高12位[整数] 低12位[小数] 即放大2^(12) - 整数部分最大为 2 ^12 -1 [最高位为符号位]
//角度标幺 按 高8位[整数] 低24位[小数] 即放大2^(24) 进行标幺
//一共迭代16次
/****************************************************************************\
Parameter/Define
\****************************************************************************/
wire [31:0] ang_p [15:0];
wire [31:0] ang_n [15:0];
localparam K = 32'h9b74ee; //K=0.607253*2^24,32'h9b74ee,
assign ang_p[0] = 32'b0_0101101_000000000000000000000000; //2D00 0000 45
assign ang_p[1] = 32'b0_0011010_100100001010011100110001; //1A90 A731 26.56505113840103 445,687,601
assign ang_p[2] = 32'b0_0001110_000010010100011101000000; //0E09 4740 14.036243438720703
assign ang_p[3] = 32'b0_0000111_001000000000000100010010; //0720 0112 7.1250163316726685
assign ang_p[4] = 32'b0_0000011_100100111000101010100110; //0393 8AA6 3.5763343572616577
assign ang_p[5] = 32'b0_0000001_110010100011011110010100; //01CA 3794 1.7899105548858643
assign ang_p[6] = 32'b0_0000000_111001010010101000011010; //00E5 2A1A 0.8951736688613892
assign ang_p[7] = 32'b0_0000000_011100101001011011010111; //0072 96D7 0.4476141333580017
assign ang_p[8] = 32'b0_0000000_001110010100101110100101; //0039 4BA5 0.22381049394607544
assign ang_p[9] = 32'b0_0000000_000111001010010111011001; //001C A5D9 0.11190563440322876
assign ang_p[10] = 32'b0_0000000_000011100101001011101101; //000E 52ED 0.05595284700393677
assign ang_p[11] = 32'b0_0000000_000001110010100101110110; //0007 2976 0.027976393699645996
assign ang_p[12] = 32'b0_0000000_000000111001010010111011; //0003 94BB 0.013988196849822998
assign ang_p[13] = 32'b0_0000000_000000011100101001011101; //0001 CA5D 0.006994098424911499
assign ang_p[14] = 32'b0_0000000_000000001110010100101110; //0000 E52E 0.0034970492124557495
assign ang_p[15] = 32'b0_0000000_000000000111001010010111; //0000 7297 0.00174852460622787475
assign ang_n[0] = 32'b1_1010011_000000000000000000000000; //complement code -45
assign ang_n[1] = 32'b1_1100101_011011110101100011001111; //complement code -26.56505113840103
assign ang_n[2] = 32'b1_1110001_111101101011100011000000; //complement code -14.036243438720703
assign ang_n[3] = 32'b1_1111000_110111111111111011101110; //complement code -7.1250163316726685
assign ang_n[4] = 32'b1_1111100_011011000111010101011010; //complement code -3.5763343572616577
assign ang_n[5] = 32'b1_1111110_001101011100100001101100; //complement code -1.7899105548858643
assign ang_n[6] = 32'b1_1111111_000110101101010111100110; //complement code -0.8951736688613892
assign ang_n[7] = 32'b1_1111111_100011010110100100101001; //complement code -0.4476141333580017
assign ang_n[8] = 32'b1_1111111_110001101011010001011011; //complement code -0.22381049394607544
assign ang_n[9] = 32'b1_1111111_111000110101101000100111; //complement code -0.11190563440322876
assign ang_n[10] = 32'b1_1111111_111100011010110100010011; //complement code -0.05595284700393677
assign ang_n[11] = 32'b1_1111111_111110001101011010001010; //complement code -0.027976393699645996
assign ang_n[12] = 32'b1_1111111_111111000110101101000101; //complement code -0.013988196849822998
assign ang_n[13] = 32'b1_1111111_111111100011010110100011; //complement code -0.006994098424911499
assign ang_n[14] = 32'b1_1111111_111111110001101011010010; //complement code -0.0034970492124557495
assign ang_n[15] = 32'b1_1111111_111111111000110101101001; //complement code -0.00174852460622787475
localparam ang_180_p = 32'b0_1011_0100_0000_0000_0000_0000_0000_000; //+180 - Q23
//localparam ang_180_n = 32'b ; //-180
reg [31:0] z_theat;
reg [4:0] iterate_times; //迭代次数最大16次数
reg cordic_start_flag;
reg signed [31:0] cordic_x;
reg signed [31:0] cordic_y;
reg signed [31:0] cordic_z;
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_start_flag <= 1'd0;
end else if(iterate_times == 5'd15) begin
cordic_start_flag <= 1'd0;
end else if(user_data_valid == 1'b1) begin
cordic_start_flag <= 1'd1;
end
end
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
iterate_times <= 5'd0;
end if(user_data_out_valid == 1'b1)begin
iterate_times <= 5'd0;
end if(cordic_start_flag == 1'b1)begin
iterate_times <= iterate_times + 5'd1;
end
end
reg [1:0] quadrant; //象限判断标志 I-00 II-10 III-11 IV-01
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
quadrant <= 2'd0;
end else if( user_data_valid == 1'b1 && iterate_times == 5'd0)begin
quadrant <= {user_x[31],user_y[31]};
end
end
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x <= 32'd0;
cordic_y <= 32'd0;
cordic_z <= 32'd0;
end else if( user_data_valid == 1'b1 && iterate_times == 5'd0)begin
case ({user_x[31],user_y[31]})
2'b00: {cordic_x,cordic_y} <= {user_x, user_y};
2'b10: {cordic_x,cordic_y} <= {{1'b0,~user_x[30:0]}+1'b1, user_y};
2'b11: {cordic_x,cordic_y} <= {{1'b0,~user_x[30:0]}+1'b1, {1'b0,~user_y[30:0]}+1'b1};
2'b01: {cordic_x,cordic_y} <= {user_x, {1'b0,~user_y[30:0]}+1'b1};
endcase
cordic_z <= 32'd0;
end else if( cordic_start_flag == 1'b1 && cordic_y[31] == 1 ) begin
cordic_x <= cordic_x - ({{cordic_y >>> iterate_times}});
cordic_y <= cordic_y + ({{cordic_x >>> iterate_times}});
cordic_z <= cordic_z + ang_n[iterate_times];
end else if( cordic_start_flag == 1'b1 && cordic_y[31] == 0 ) begin
cordic_x <= cordic_x + ({{cordic_y >>> iterate_times}});
cordic_y <= cordic_y - ({{cordic_x >>> iterate_times}});
cordic_z <= cordic_z + ang_p[iterate_times];
end
end
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
user_data_out_valid <= 1'b0;
end else if(iterate_times == 5'd15)begin
user_data_out_valid <= 1'b1;
end else begin
user_data_out_valid <= 1'b0;
end
end
always @(*) begin
if(user_data_out_valid == 1'b1)begin
case (quadrant)
2'b00 : user_theat = (cordic_z >>>24);
2'b10 : user_theat = (ang_180_p - (cordic_z >>>1)) >>> 23;
2'b11 : user_theat = (ang_180_p + (cordic_z >>>1)) >>> 23;
2'b01 : user_theat = (~(cordic_z>>>24)) + 1'b1 ;
endcase
end
end
//输出*0.607253
assign user_len =(user_data_out_valid == 1'b1)? ( (cordic_x >>> 1) + (cordic_x >>> 4) + (cordic_x >>> 5) +(cordic_x >>> 7) + (cordic_x >>> 8) + (cordic_x >>> 10)+(cordic_x >>> 11) + (cordic_x >>> 12)):32'd0;
endmodule
ii、FPGA流水线实现cordic
module cordic_parallel(
input sys_clk ,
input sys_rst_n ,
input user_data_valid,
input [31:0] user_x,
input [31:0] user_y,
output reg user_data_out_valid,
output reg [31:0] user_theat,
output [31:0] user_len
);
//输入为有符号数(定点数) 高12位[整数] 低12位[小数] 即放大2^(12) - 整数部分最大为 2 ^12 -1 [最高位为符号位]
//角度标幺 按 高8位[整数] 低24位[小数] 即放大2^(24) 进行标幺
//一共迭代16次
/****************************************************************************\
Parameter/Define
\****************************************************************************/
wire [31:0] ang_p [15:0];
wire [31:0] ang_n [15:0];
localparam K = 32'h9b74ee; //K=0.607253*2^24,32'h9b74ee,
assign ang_p[0] = 32'b0_0101101_000000000000000000000000; //2D00 0000 45
assign ang_p[1] = 32'b0_0011010_100100001010011100110001; //1A90 A731 26.56505113840103 445,687,601
assign ang_p[2] = 32'b0_0001110_000010010100011101000000; //0E09 4740 14.036243438720703
assign ang_p[3] = 32'b0_0000111_001000000000000100010010; //0720 0112 7.1250163316726685
assign ang_p[4] = 32'b0_0000011_100100111000101010100110; //0393 8AA6 3.5763343572616577
assign ang_p[5] = 32'b0_0000001_110010100011011110010100; //01CA 3794 1.7899105548858643
assign ang_p[6] = 32'b0_0000000_111001010010101000011010; //00E5 2A1A 0.8951736688613892
assign ang_p[7] = 32'b0_0000000_011100101001011011010111; //0072 96D7 0.4476141333580017
assign ang_p[8] = 32'b0_0000000_001110010100101110100101; //0039 4BA5 0.22381049394607544
assign ang_p[9] = 32'b0_0000000_000111001010010111011001; //001C A5D9 0.11190563440322876
assign ang_p[10] = 32'b0_0000000_000011100101001011101101; //000E 52ED 0.05595284700393677
assign ang_p[11] = 32'b0_0000000_000001110010100101110110; //0007 2976 0.027976393699645996
assign ang_p[12] = 32'b0_0000000_000000111001010010111011; //0003 94BB 0.013988196849822998
assign ang_p[13] = 32'b0_0000000_000000011100101001011101; //0001 CA5D 0.006994098424911499
assign ang_p[14] = 32'b0_0000000_000000001110010100101110; //0000 E52E 0.0034970492124557495
assign ang_p[15] = 32'b0_0000000_000000000111001010010111; //0000 7297 0.00174852460622787475
assign ang_n[0] = 32'b1_1010011_000000000000000000000000; //complement code -45
assign ang_n[1] = 32'b1_1100101_011011110101100011001111; //complement code -26.56505113840103
assign ang_n[2] = 32'b1_1110001_111101101011100011000000; //complement code -14.036243438720703
assign ang_n[3] = 32'b1_1111000_110111111111111011101110; //complement code -7.1250163316726685
assign ang_n[4] = 32'b1_1111100_011011000111010101011010; //complement code -3.5763343572616577
assign ang_n[5] = 32'b1_1111110_001101011100100001101100; //complement code -1.7899105548858643
assign ang_n[6] = 32'b1_1111111_000110101101010111100110; //complement code -0.8951736688613892
assign ang_n[7] = 32'b1_1111111_100011010110100100101001; //complement code -0.4476141333580017
assign ang_n[8] = 32'b1_1111111_110001101011010001011011; //complement code -0.22381049394607544
assign ang_n[9] = 32'b1_1111111_111000110101101000100111; //complement code -0.11190563440322876
assign ang_n[10] = 32'b1_1111111_111100011010110100010011; //complement code -0.05595284700393677
assign ang_n[11] = 32'b1_1111111_111110001101011010001010; //complement code -0.027976393699645996
assign ang_n[12] = 32'b1_1111111_111111000110101101000101; //complement code -0.013988196849822998
assign ang_n[13] = 32'b1_1111111_111111100011010110100011; //complement code -0.006994098424911499
assign ang_n[14] = 32'b1_1111111_111111110001101011010010; //complement code -0.0034970492124557495
assign ang_n[15] = 32'b1_1111111_111111111000110101101001; //complement code -0.00174852460622787475
localparam ang_180_p = 32'b0_1011_0100_0000_0000_0000_0000_0000_000; //+180 - Q23
//象限判断标志 I-00 II-10 III-11 IV-01
//16-level-pipelevel
reg signed [31:0] cordic_x0 ,cordic_y0 ,cordic_z0 ,quadrant_0 ;
reg signed [31:0] cordic_x1 ,cordic_y1 ,cordic_z1 ,quadrant_1 ;
reg signed [31:0] cordic_x2 ,cordic_y2 ,cordic_z2 ,quadrant_2 ;
reg signed [31:0] cordic_x3 ,cordic_y3 ,cordic_z3 ,quadrant_3 ;
reg signed [31:0] cordic_x4 ,cordic_y4 ,cordic_z4 ,quadrant_4 ;
reg signed [31:0] cordic_x5 ,cordic_y5 ,cordic_z5 ,quadrant_5 ;
reg signed [31:0] cordic_x6 ,cordic_y6 ,cordic_z6 ,quadrant_6 ;
reg signed [31:0] cordic_x7 ,cordic_y7 ,cordic_z7 ,quadrant_7 ;
reg signed [31:0] cordic_x8 ,cordic_y8 ,cordic_z8 ,quadrant_8 ;
reg signed [31:0] cordic_x9 ,cordic_y9 ,cordic_z9 ,quadrant_9 ;
reg signed [31:0] cordic_x10,cordic_y10,cordic_z10,quadrant_10;
reg signed [31:0] cordic_x11,cordic_y11,cordic_z11,quadrant_11;
reg signed [31:0] cordic_x12,cordic_y12,cordic_z12,quadrant_12;
reg signed [31:0] cordic_x13,cordic_y13,cordic_z13,quadrant_13;
reg signed [31:0] cordic_x14,cordic_y14,cordic_z14,quadrant_14;
reg signed [31:0] cordic_x15,cordic_y15,cordic_z15,quadrant_15;
reg signed [31:0] cordic_x16,cordic_y16,cordic_z16,quadrant_16;
//reg [1:0] quadrant; //象限判断标志 I-00 II-10 III-11 IV-01
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
quadrant_0 <= 2'd0;
end else if( user_data_valid == 1'b1)begin
quadrant_0 <= {user_x[31],user_y[31]};
end
end
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x0 <= 32'd0;
cordic_y0 <= 32'd0;
cordic_z0 <= 32'd0;
end else if( user_data_valid == 1'b1)begin
case ({user_x[31],user_y[31]})
2'b00: {cordic_x0,cordic_y0} <= {user_x, user_y};
2'b10: {cordic_x0,cordic_y0} <= {{1'b0,~user_x[30:0]}+1'b1, user_y};
2'b11: {cordic_x0,cordic_y0} <= {{1'b0,~user_x[30:0]}+1'b1, {1'b0,~user_y[30:0]}+1'b1};
2'b01: {cordic_x0,cordic_y0} <= {user_x, {1'b0,~user_y[30:0]}+1'b1};
endcase
cordic_z0 <= 32'd0;
end
end
//iterate 1
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x1 <= 32'd0;
cordic_y1 <= 32'd0;
cordic_z1 <= 32'd0;
end else if(cordic_y0[31] == 1) begin
cordic_x1 <= cordic_x0 - ({{cordic_y0 >>> 0}});
cordic_y1 <= cordic_y0 + ({{cordic_x0 >>> 0}});
cordic_z1 <= cordic_z0 + ang_n[0];
end else if(cordic_y0[31] == 0) begin
cordic_x1 <= cordic_x0 + ({{cordic_y0 >>> 0}});
cordic_y1 <= cordic_y0 - ({{cordic_x0 >>> 0}});
cordic_z1 <= cordic_z0 + ang_p[0];
end
end
//iterate 2
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x2 <= 32'd0;
cordic_y2 <= 32'd0;
cordic_z2 <= 32'd0;
end else if(cordic_y1[31] == 1) begin
cordic_x2 <= cordic_x1 - ({{cordic_y1 >>> 1}});
cordic_y2 <= cordic_y1 + ({{cordic_x1 >>> 1}});
cordic_z2 <= cordic_z1 + ang_n[1];
end else if(cordic_y1[31] == 0) begin
cordic_x2 <= cordic_x1 + ({{cordic_y1 >>> 1}});
cordic_y2 <= cordic_y1 - ({{cordic_x1 >>> 1}});
cordic_z2 <= cordic_z1 + ang_p[1];
end
end
//iterate 3
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x3 <= 32'd0;
cordic_y3 <= 32'd0;
cordic_z3 <= 32'd0;
end else if(cordic_y2[31] == 1) begin
cordic_x3 <= cordic_x2 - ({{cordic_y2 >>> 2}});
cordic_y3 <= cordic_y2 + ({{cordic_x2 >>> 2}});
cordic_z3 <= cordic_z2 + ang_n[2];
end else if(cordic_y2[31] == 0) begin
cordic_x3 <= cordic_x2 + ({{cordic_y2 >>> 2}});
cordic_y3 <= cordic_y2 - ({{cordic_x2 >>> 2}});
cordic_z3 <= cordic_z2 + ang_p[2];
end
end
//iterate 4
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x4 <= 32'd0;
cordic_y4 <= 32'd0;
cordic_z4 <= 32'd0;
end else if(cordic_y3[31] == 1) begin
cordic_x4 <= cordic_x3 - ({{cordic_y3 >>> 3}});
cordic_y4 <= cordic_y3 + ({{cordic_x3 >>> 3}});
cordic_z4 <= cordic_z3 + ang_n[3];
end else if(cordic_y3[31] == 0) begin
cordic_x4 <= cordic_x3 + ({{cordic_y3 >>> 3}});
cordic_y4 <= cordic_y3 - ({{cordic_x3 >>> 3}});
cordic_z4 <= cordic_z3 + ang_p[3];
end
end
//iterate 5
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x5 <= 32'd0;
cordic_y5 <= 32'd0;
cordic_z5 <= 32'd0;
end else if(cordic_y4[31] == 1) begin
cordic_x5 <= cordic_x4 - ({{cordic_y4 >>> 4}});
cordic_y5 <= cordic_y4 + ({{cordic_x4 >>> 4}});
cordic_z5 <= cordic_z4 + ang_n[4];
end else if(cordic_y4[31] == 0) begin
cordic_x5 <= cordic_x4 + ({{cordic_y4 >>> 4}});
cordic_y5 <= cordic_y4 - ({{cordic_x4 >>> 4}});
cordic_z5 <= cordic_z4 + ang_p[4];
end
end
//iterate 6
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x6 <= 32'd0;
cordic_y6 <= 32'd0;
cordic_z6 <= 32'd0;
end else if(cordic_y5[31] == 1) begin
cordic_x6 <= cordic_x5 - ({{cordic_y5 >>> 5}});
cordic_y6 <= cordic_y5 + ({{cordic_x5 >>> 5}});
cordic_z6 <= cordic_z5 + ang_n[5];
end else if(cordic_y5[31] == 0) begin
cordic_x6 <= cordic_x5 + ({{cordic_y5 >>> 5}});
cordic_y6 <= cordic_y5 - ({{cordic_x5 >>> 5}});
cordic_z6 <= cordic_z5 + ang_p[5];
end
end
//iterate 7
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x7 <= 32'd0;
cordic_y7 <= 32'd0;
cordic_z7 <= 32'd0;
end else if(cordic_y6[31] == 1) begin
cordic_x7 <= cordic_x6 - ({{cordic_y6 >>> 6}});
cordic_y7 <= cordic_y6 + ({{cordic_x6 >>> 6}});
cordic_z7 <= cordic_z6 + ang_n[6];
end else if(cordic_y6[31] == 0) begin
cordic_x7 <= cordic_x6 + ({{cordic_y6 >>> 6}});
cordic_y7 <= cordic_y6 - ({{cordic_x6 >>> 6}});
cordic_z7 <= cordic_z6 + ang_p[6];
end
end
//iterate 8
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x8 <= 32'd0;
cordic_y8 <= 32'd0;
cordic_z8 <= 32'd0;
end else if(cordic_y7[31] == 1) begin
cordic_x8 <= cordic_x7 - ({{cordic_y7 >>> 7}});
cordic_y8 <= cordic_y7 + ({{cordic_x7 >>> 7}});
cordic_z8 <= cordic_z7 + ang_n[7];
end else if(cordic_y7[31] == 0) begin
cordic_x8 <= cordic_x7 + ({{cordic_y7 >>> 7}});
cordic_y8 <= cordic_y7 - ({{cordic_x7 >>> 7}});
cordic_z8 <= cordic_z7 + ang_p[7];
end
end
//iterate 9
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x9 <= 32'd0;
cordic_y9 <= 32'd0;
cordic_z9 <= 32'd0;
end else if(cordic_y8[31] == 1) begin
cordic_x9 <= cordic_x8 - ({{cordic_y8 >>> 8}});
cordic_y9 <= cordic_y8 + ({{cordic_x8 >>> 8}});
cordic_z9 <= cordic_z8 + ang_n[8];
end else if(cordic_y8[31] == 0) begin
cordic_x9 <= cordic_x8 + ({{cordic_y8 >>> 8}});
cordic_y9 <= cordic_y8 - ({{cordic_x8 >>> 8}});
cordic_z9 <= cordic_z8 + ang_p[8];
end
end
//iterate 10
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x10 <= 32'd0;
cordic_y10 <= 32'd0;
cordic_z10 <= 32'd0;
end else if(cordic_y9[31] == 1) begin
cordic_x10 <= cordic_x9 - ({{cordic_y9 >>> 9}});
cordic_y10 <= cordic_y9 + ({{cordic_x9 >>> 9}});
cordic_z10 <= cordic_z9 + ang_n[9];
end else if(cordic_y9[31] == 0) begin
cordic_x10 <= cordic_x9 + ({{cordic_y9 >>> 9}});
cordic_y10 <= cordic_y9 - ({{cordic_x9 >>> 9}});
cordic_z10 <= cordic_z9 + ang_p[9];
end
end
//iterate 11
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x11 <= 32'd0;
cordic_y11 <= 32'd0;
cordic_z11 <= 32'd0;
end else if(cordic_y10[31] == 1) begin
cordic_x11 <= cordic_x10 - ({{cordic_y10 >>> 10}});
cordic_y11 <= cordic_y10 + ({{cordic_x10 >>> 10}});
cordic_z11 <= cordic_z10 + ang_n[10];
end else if(cordic_y10[31] == 0) begin
cordic_x11 <= cordic_x10 + ({{cordic_y10 >>> 10}});
cordic_y11 <= cordic_y10 - ({{cordic_x10 >>> 10}});
cordic_z11 <= cordic_z10 + ang_p[10];
end
end
//iterate 12
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x12 <= 32'd0;
cordic_y12 <= 32'd0;
cordic_z12 <= 32'd0;
end else if(cordic_y11[31] == 1) begin
cordic_x12 <= cordic_x11 - ({{cordic_y11 >>> 11}});
cordic_y12 <= cordic_y11 + ({{cordic_x11 >>> 11}});
cordic_z12 <= cordic_z11 + ang_n[11];
end else if(cordic_y11[31] == 0) begin
cordic_x12 <= cordic_x11 + ({{cordic_y11 >>> 11}});
cordic_y12 <= cordic_y11 - ({{cordic_x11 >>> 11}});
cordic_z12 <= cordic_z11 + ang_p[11];
end
end
//iterate 13
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x13 <= 32'd0;
cordic_y13 <= 32'd0;
cordic_z13 <= 32'd0;
end else if(cordic_y12[31] == 1) begin
cordic_x13 <= cordic_x12 - ({{cordic_y12 >>> 12}});
cordic_y13 <= cordic_y12 + ({{cordic_x12 >>> 12}});
cordic_z13 <= cordic_z12 + ang_n[12];
end else if(cordic_y12[31] == 0) begin
cordic_x13 <= cordic_x12 + ({{cordic_y12 >>> 12}});
cordic_y13 <= cordic_y12 - ({{cordic_x12 >>> 12}});
cordic_z13 <= cordic_z12 + ang_p[12];
end
end
//iterate 14
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x14 <= 32'd0;
cordic_y14 <= 32'd0;
cordic_z14 <= 32'd0;
end else if(cordic_y13[31] == 1) begin
cordic_x14 <= cordic_x13 - ({{cordic_y13 >>> 13}});
cordic_y14 <= cordic_y13 + ({{cordic_x13 >>> 13}});
cordic_z14 <= cordic_z13 + ang_n[13];
end else if(cordic_y13[31] == 0) begin
cordic_x14 <= cordic_x13 + ({{cordic_y13 >>> 13}});
cordic_y14 <= cordic_y13 - ({{cordic_x13 >>> 13}});
cordic_z14 <= cordic_z13 + ang_p[13];
end
end
//iterate 15
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x15 <= 32'd0;
cordic_y15 <= 32'd0;
cordic_z15 <= 32'd0;
end else if(cordic_y14[31] == 1) begin
cordic_x15 <= cordic_x14 - ({{cordic_y14 >>> 14}});
cordic_y15 <= cordic_y14 + ({{cordic_x14 >>> 14}});
cordic_z15 <= cordic_z14 + ang_n[14];
end else if(cordic_y14[31] == 0) begin
cordic_x15 <= cordic_x14 + ({{cordic_y14 >>> 14}});
cordic_y15 <= cordic_y14 - ({{cordic_x14 >>> 14}});
cordic_z15 <= cordic_z14 + ang_p[14];
end
end
//iterate 16
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
cordic_x16 <= 32'd0;
cordic_y16 <= 32'd0;
cordic_z16 <= 32'd0;
end else if(cordic_y15[31] == 1) begin
cordic_x16 <= cordic_x15 - ({{cordic_y15 >>> 15}});
cordic_y16 <= cordic_y15 + ({{cordic_x15 >>> 15}});
cordic_z16 <= cordic_z15 + ang_n[15];
end else if(cordic_y15[31] == 0) begin
cordic_x16 <= cordic_x15 + ({{cordic_y15 >>> 15}});
cordic_y16 <= cordic_y15 - ({{cordic_x15 >>> 15}});
cordic_z16 <= cordic_z15 + ang_p[15];
end
end
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
{quadrant_1, quadrant_2, quadrant_3, quadrant_4} <= 4'b0;
{quadrant_5, quadrant_6, quadrant_7, quadrant_8} <= 4'b0;
{quadrant_9, quadrant_10, quadrant_11, quadrant_12} <= 4'b0;
{quadrant_13, quadrant_14, quadrant_15, quadrant_16} <= 4'b0;
end else begin
{quadrant_1, quadrant_2, quadrant_3, quadrant_4 } <= {quadrant_0, quadrant_1, quadrant_2, quadrant_3 };
{quadrant_5, quadrant_6, quadrant_7, quadrant_8 } <= {quadrant_4, quadrant_5, quadrant_6, quadrant_7 };
{quadrant_9, quadrant_10, quadrant_11, quadrant_12} <= {quadrant_8, quadrant_9, quadrant_10, quadrant_11};
{quadrant_13, quadrant_14, quadrant_15, quadrant_16} <= {quadrant_12, quadrant_13, quadrant_14, quadrant_15};
end
end
reg [4:0] iterate_times;
reg start_flag;
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
start_flag <= 1'd0;
end else if(user_data_valid == 1'b1) begin
start_flag = 1'd1;
end
end
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
iterate_times <= 5'd0;
end else if(iterate_times >= 5'd17) begin
iterate_times = 5'd17;
end else if(user_data_valid == 1'b1 || start_flag == 1'b1 ) begin
iterate_times <= iterate_times + 5'd1;
end
end
always @(posedge sys_clk or negedge sys_rst_n) begin
if(!sys_rst_n)begin
user_data_out_valid <= 1'b0;
end else if(iterate_times >= 5'd16)begin
user_data_out_valid <= 1'b1;
end else begin
user_data_out_valid <= 1'b0;
end
end
always @(*) begin
if(user_data_out_valid == 1'b1)begin
case (quadrant_16)
2'b00 : user_theat = (cordic_z16 >>>24);
2'b10 : user_theat = (ang_180_p - (cordic_z16 >>>1)) >>> 23;
2'b11 : user_theat = (ang_180_p + (cordic_z16 >>>1)) >>> 23;
2'b01 : user_theat = (~(cordic_z16>>>24)) + 1'b1 ;
endcase
end
end
//输出*0.607253
assign user_len =(user_data_out_valid == 1'b1)? ( (cordic_x16 >>> 1) + (cordic_x16 >>> 4) + (cordic_x16 >>> 5) +(cordic_x16 >>> 7) + (cordic_x16 >>> 8) + (cordic_x16 >>> 10)+(cordic_x16 >>> 11) + (cordic_x16 >>> 12)):32'd0;
endmodule
以上实现一定要注意不能运算溢出,一旦溢出将影响相应判断。