CCSU欢迎你们哟

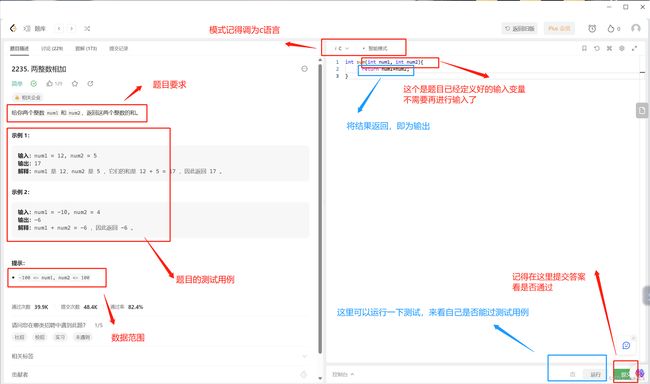
新生ccsu们~对于力扣的话，其实很简单，你要输出的值基本用return来返回，然后给出输入的值已经不需要你输入啦，这个上面都有，其他的你只要写题目要求的代码就好啦~~ 

题目：2235.两数相加

链接：https://leetcode.cn/problems/add-two-integers/description/

解题思路： 

这个题目的话就是很简单的传说中小学生的题目，加法题目，简称:A+B；

做法的话也很简单也就是a+b；

这里可以用一个变量去承载结果进行返回，也能之间返回结果；

直接返回的话就会有个好处，节省了内存空间（这个可以到时候提交试试看，对比两者的空间使用），原因的话就是直接返回，就没用申请一个int的空间啦~

代码如下： 

①直接返回版本：

int sum(int num1, int num2){
      return num1+num2;
}

 ②用变量承载返回：

int sum(int num1, int num2){
      int ans;
      ans=num1+num2; 
      return ans;
}

题目： 2413.最小偶倍数

链接：https://leetcode.cn/problems/smallest-even-multiple/description/

解题思路： 

 我们可知对于任意两个正整数 a，b 的最小公倍数为 ,为a,b的最大公约数

最小公倍数：最小公倍数（Least Common Multiple）是一种数学概念，是指两个或多个整数公有的倍数中，除0以外最小的一个公倍数。 例如：4   20的最小公倍数就是20； 

最大公约数：也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。例如：4   20的最小公倍数就是4； 

因为题目中是求2与n的最小公倍数，因此公式可变为;

我们又可以发现

①当n为偶数时，2与n的最大公约数就是2，例如：2  20的最大公约数就是2，因此在n为偶数时恒等于2，因此最小公倍数等于；

②当n为奇数时，2与n的最大公约数就是1，因为奇数与2的公约数只有1，例如 7  2的最大公约数是1，因此在n为奇数时恒等于1，因此最小公倍数等于；

因此总结，只要判断n奇偶性就能解决这个题目啦~

代码如下：

int smallestEvenMultiple(int n){
    int t;
    if(n%2==0){
        t=n;
    }else{
        t=2*n;
    }
    return t;
}

题目：2651.计算列车到站时间 

链接：https://leetcode.cn/problems/calculate-delayed-arrival-time/description/ 

解题思路： 

这个题目因为给出的都是整点的时间，因此很简单，直接加(sum=arrivalTime+delayedTime)用判断语句来判断各种情况就好，总共有三种情况：

①当总时间sum小于24时，说明没用超过一天的，直接返回就行；

②当总时间sum等于24时，说明到了第二天，因为是24小时制，所以得清零，返回0即可

③当总时间sum大于24时，说明到了第二天，时间得减去24小时，才能返回

代码如下：

int findDelayedArrivalTime(int arrivalTime, int delayedTime){
    int sum=arrivalTime+delayedTime;
        int t;
        if(sum<24){
            t=sum;
        }else if(t==24){
            t=0;
        }else{
            t=sum-24;
        }
        return t;
}

题目： 2769.找出最大的可达成数字

链接：https://leetcode.cn/problems/find-the-maximum-achievable-number/description/

解题思路： 

根据题目可知要求最大的可达成数字的话，那么x一定是大于num的，所以对呀x肯定是减，对于num肯定是加，因此可知每一次操作，num减1，x加1，因此num与x相差2，因次经过t次，num与x相差2t，因此可知 

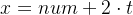
代码如下：

int theMaximumAchievableX(int num, int t){
     return num+2*t;
}

 题目：2652.倍数求和

链接：https://leetcode.cn/problems/sum-multiples/description/

解题思路： 

首先看一下数据，n的范围不超过，因此可以暴力循环解题

从1到n循环，当能被3、5、7整除的时候，就起来求和，最好返回结果

代码如下：

int sumOfMultiples(int n){
     int sum=0;
        for(int i=1;i<=n;i++)
        {
            if(i%3==0 || i%5==0 || i%7==0)
            {
                sum+=i;
            }
        }
        return sum;
}

题目： 1342.将数字变为0的操作次数

链接：https://leetcode.cn/problems/number-of-steps-to-reduce-a-number-to-zero/description/

解题思路： 

 就算按照题目要求进行两步操作：

 如果当前数字是偶数，你需要把它除以 2 ；否则，减去 1 

用一个循环来控制，条件就是当数值不为0或者大于0（这个地方循环条件一定不能等于0不然会无限循环的），每一次操作结束记得计数

代码如下：

int numberOfSteps(int num){
    int cnt=0;
	while(num!=0)
	{
		if(num%2==0)
          {
             num/=2;
          }
        else
          {
             num-=1;
          }
        cnt++;
    }
    return cnt;
}

题目： 1688.比赛中配对次数

链接：https://leetcode.cn/problems/count-of-matches-in-tournament/description/

解题思路： 

每一场比赛中，输的队伍无法晋级且不会再参加后续的比赛。因为最后只决出一个获胜队伍，因此就有n-1 个无法晋级的队伍，所以就会有n-1场比赛。

代码如下：

int numberOfMatches(int n){
    return n-1;
}

 题目：2427.公因数的数目

链接：https://leetcode.cn/problems/number-of-common-factors/

解题思路： 

方法1： 由于 a 和 b的公因子一定不会超过 a和 b，因此我们只需要在 [1,fmin⁡(a,b)中枚举 i，并判断 i 是否为公因子。(fmin)为c语言自带函数，用于找出最小值的。

代码如下：

int commonFactors(int a, int b){
    int ans = 0;
        for (int i = 1; i <= fmin(a, b); i++) {
            if (a % i == 0 && b % i == 0) {
                ans++;
            }
        }
        return ans;
}

方法2：就是用一个数组来标记一个数的公因数，在到第二个数的公因数里面判断有没有共同的

代码如下： 

int commonFactors(int a, int b){
    int sum[1005]={0};
        int cnt=0;
        for(int i=1;i<=a;i++)
        {
            if(a%i==0)
            {
                sum[a/i]++;
            }
        }
        for(int i=1;i<=b;i++)
        {
            if(b%i==0)
            {
                if(sum[b/i]!=0)
                {
                    cnt++;
                }
            }
        }
        return cnt;
}

题目： 1523.在区间范围内统计奇数数目

链接：https://leetcode.cn/problems/count-odd-numbers-in-an-interval-range/description/

解题思路： 

方法1：暴力循环

看了下数据最大数值达到了，如何用单纯的循环肯定会超时，因为一般的循环最大的界值在左右，因此这个地方我们肯定要处理数据的，如果用暴力的话，因为我们是求得奇数，所以我们完全可以从确定奇数开始，然后循环每次+2，使得每次都是奇数，减少循环的次数

我们一定得养成看数据的习惯！！！！

代码如下：

int countOdds(int low, int high){
    int cnt=0;
        if(low%2==0)
        {
            low=low+1;
        }
        for(int i=low;i<=high;i=i+2)
        {
            cnt++;
        }
        return cnt;
}

方法2：规律

 我们可以用将[0,high]中的奇数个数减去[0,low)中的奇数个数：

代码如下：

int countOdds(int low, int high){
    return ((high+1)/2-low/2);
}

题目： 2485.找出中枢整数

链接：https://leetcode.cn/problems/find-the-pivot-integer/description/

 解题思路：

方法1：前缀和

这个地方我运用了前缀和的思想，用sum数组记录每一次的和，然后去判断当总和减去前一个和是否等于当前的和 ，来记录等于当前和的下标，这个就是我们要找的x

测试例图如下：

代码如下：

int pivotInteger(int n){
     int sum[50010]={0};
        for(int i=1;i<=n;i++)
        {
            sum[i]=sum[i-1]+i;
        }
        int x=0;
        for(int i=1;i<=n;i++)
        {
            int ans=sum[n]-sum[i-1];
            if(sum[i]==ans)
            {
                x=i;
                break;
            }
        }
        if(x==0)
        {
            return -1;
        }
        return x;
}

方法2：数学方法归纳

根据方法1的思想我们可知，其实只要我们判断1到x的和是否等于（1到n的和减去1到（x-1）的和），因为我们可以发现1到x的和为,1到n的和为,1到x-1的和为,因此判断条件就算判断和是否相等，相等时的x就是我们要求的中枢x，因此可以化简为,当然这个地方还有个小细节就算判断能不能开根号，能的话返回x；不能的话，则没有中枢x，返回-1

sqrt函数是c语言自带的开根号的函数

代码如下：

int pivotInteger(int n){
    int m = n * (n + 1) / 2;
    int x = sqrt(m);
    if(x*x==m)
    {
        return x;
    }
    else
    {
        return -1;
    }
}

最后： 欢迎学弟学妹来到计科学院这个大家庭，大家努力~~在长大一起长大~！

数据很重要，记得养成这个习惯！！对于以后很重要哈~