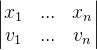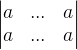卡尔曼滤波算法包(python)
本文写了具有普遍适用性的卡尔曼滤波(Kalman filter)算法程序包,输入参数即可进行运算。
算法可参考资料:
算法推导:
卡尔曼滤波的理解、推导和应用
卡尔曼滤波
参数理解:
卡尔曼滤波的理解以及参数调整
手把手教你学-卡尔曼滤波(附代码)
其中![]() ,
,![]() 为仪器观测到的状态值
为仪器观测到的状态值
输入参数:
状态矩阵x
状态转移矩阵A
输入控制矩阵B
外界对系统作用矩阵u
初始误差协方差矩阵P
预测噪声协方差矩阵Q
观测矩阵H
观测噪声协方差矩阵R
(可通过调整三个协方差矩阵大小来调整降噪效果)
可复制算法包:
def Kalmanfilter(x):
# 需预先定义以下变量:
# 状态转移矩阵A
# 输入控制矩阵B
# 外界对系统作用矩阵u
# 误差协方差矩阵P
# 预测噪声协方差矩阵Q
# 观测矩阵H
# 观测噪声协方差矩阵R
# import numpy as np
xr = np.shape(x)[0] # 调用状态矩阵行数
xc = np.shape(x)[1] # 调用状态矩阵列数
X_mat = x.copy() # 初始化记录系统优化状态值的矩阵(浅拷贝)
X = x.T[0].T # 抽取预测优化值的初始状态值
Z = H * x
global P #初始设置为全局变量P
for i in range(1,xc):
# 预测
X_predict = A * X # 估算状态变量
if B!=0:
X_predict = A * X + B * u.T[i-1].T
P_predict = A * P * A.T + Q # 估算状态误差协方差
# 校正
K = P_predict * H.T / (H * P_predict * H.T + R) # 更新卡尔曼增益
X = X_predict + K * (Z.T[i].T - H * X_predict) # 更新预测优化值
P = (np.eye(xr) - K * H) * P_predict # 更新状态误差协方差
# 记录系统的预测优化值
for j in range(xr):
X_mat[j, i] = X[j, 0]
Z_mat = H * X_mat
return Z_mat
kf = Kalmanfilter(x)案例:对均加速直线运动的位置进行降噪处理,加速度为1,初始时间为0,初始位置为0,观测时间为7秒,每0.1秒观测一次,设误差为白噪声N(0,1)
方法1
设置时间跳跃系统:(s为位置,v为速度)
状态矩阵x:
状态转移矩阵A:
控制矩阵B:
外界对系统作用矩阵u:
初始误差协方差矩阵P:
预测噪声协方差矩阵Q:
观测矩阵H:
![]()
观测噪声协方差矩阵R:
![]()
import numpy as np
import matplotlib.pyplot as plt
delta_t = 0.1 # 每秒钟采一次样
end_t = 7 # 时间长度
time_t = end_t * 10 # 采样次数
t = np.arange(0, end_t, delta_t) # 设置时间数组
v_var = 1 # 测量噪声的方差
v_noise = np.round(np.random.normal(0, v_var, time_t), 2)# 定义测量噪声
a=1 #加速度
vn=np.add((1 / 2*a * t ** 2) , v_noise) # 定义仪器测量的位置
v=a*t #定义速度数组
x = np.mat([vn,v]) # 定义状态矩阵
xc = np.shape(x)[1] #调用状态矩阵列数
u1=np.linspace(a,a,xc)
u = np.mat([u1,u1]) # 定义外界对系统作用矩阵
A = np.mat([[1, delta_t], [0, 1]]) # 定义状态转移矩阵
B = [[1 / 2 * (delta_t ** 2),0],[0,delta_t]]# 定义输入控制矩阵
P = np.mat([[1, 0], [0, 1]]) # 定义初始状态协方差矩阵
Q = np.mat([[0.001, 0], [0, 0.001]]) # 定义状态转移(预测噪声)协方差矩阵
H = np.mat([1, 0]) # 定义观测矩阵
R = np.mat([1]) # 定义观测噪声协方差矩阵
def Kalmanfilter(x):
# 需预先定义以下变量:
# 状态转移矩阵A
# 输入控制矩阵B
# 外界对系统作用矩阵u
# 误差协方差矩阵P
# 预测噪声协方差矩阵Q
# 观测矩阵H
# 观测噪声协方差矩阵R
# import numpy as np
xr = np.shape(x)[0] # 调用状态矩阵行数
xc = np.shape(x)[1] # 调用状态矩阵列数
X_mat = x.copy() # 初始化记录系统优化状态值的矩阵(浅拷贝)
X = x.T[0].T # 抽取预测优化值的初始状态值
Z = H * x
global P #初始设置为全局变量P
for i in range(1,xc):
# 预测
X_predict = A * X # 估算状态变量
if B!=0:
X_predict = A * X + B * u.T[i-1].T
P_predict = A * P * A.T + Q # 估算状态误差协方差
# 校正
K = P_predict * H.T / (H * P_predict * H.T + R) # 更新卡尔曼增益
X = X_predict + K * (Z.T[i].T - H * X_predict) # 更新预测优化值
P = (np.eye(xr) - K * H) * P_predict # 更新状态误差协方差
# 记录系统的预测优化值
for j in range(xr):
X_mat[j, i] = X[j, 0]
Z_mat = H * X_mat
return Z_mat
kf=Kalmanfilter(x)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置正常显示中文
plt.plot(t,np.array(kf)[0], "g", label='预测优化值')
plt.plot(t,np.array(x[0])[0], "r--", label='测量值')
plt.xlabel("时间") # 设置X轴的名字
plt.ylabel("位移") # 设置Y轴的名字
plt.title("卡尔曼滤波示意图") # 设置标题
plt.legend() # 设置图例
plt.show() # 显示图表方法2
设置时间跳跃系统:(s为位置,v为速度)
状态矩阵x:
状态转移矩阵A:
控制矩阵B:
![]()
外界对系统作用矩阵u:
![]()
初始误差协方差矩阵P:
预测噪声协方差矩阵Q:
观测矩阵H:
![]()
观测噪声协方差矩阵R:
![]()
import numpy as np
import matplotlib.pyplot as plt
delta_t = 0.1 # 每秒钟采一次样
end_t = 7 # 时间长度
time_t = end_t * 10 # 采样次数
t = np.arange(0, end_t, delta_t) # 设置时间数组
v_var = 1 # 测量噪声的方差
v_noise = np.round(np.random.normal(0, v_var, time_t), 2)# 定义测量噪声
a=1 #加速度
vn=np.add((1 / 2*a * t ** 2) , v_noise) # 定义仪器测量的位置
v=a*t #定义速度数组
a1=np.linspace(a,a,time_t)
x = np.mat([vn,v,a1]) # 定义状态矩阵
u = 0 # 定义外界对系统作用矩阵
A = np.mat([[1, delta_t, 1/2*delta_t], [0, 1, delta_t], [0, 0, 1]]) # 定义状态转移矩阵
B = 0 # 定义输入控制矩阵
P = np.mat([[1, 0,0], [0, 1,0],[0,0,1]]) # 定义初始状态协方差矩阵
Q = np.mat([[0.001, 0,0], [0, 0.001,0],[0,0,0.001]]) # 定义状态转移(预测噪声)协方差矩阵
H = np.mat([1, 0, 0]) # 定义观测矩阵
R = np.mat([1]) # 定义观测噪声协方差矩阵
def Kalmanfilter(x):
# 需预先定义以下变量:
# 状态转移矩阵A
# 输入控制矩阵B
# 外界对系统作用矩阵u
# 误差协方差矩阵P
# 预测噪声协方差矩阵Q
# 观测矩阵H
# 观测噪声协方差矩阵R
# import numpy as np
xr = np.shape(x)[0] # 调用状态矩阵行数
xc = np.shape(x)[1] # 调用状态矩阵列数
X_mat = x.copy() # 初始化记录系统优化状态值的矩阵(浅拷贝)
X = x.T[0].T # 抽取预测优化值的初始状态值
Z = H * x
global P #初始设置为全局变量P
for i in range(1,xc):
# 预测
X_predict = A * X # 估算状态变量
if B!=0:
X_predict = A * X + B * u.T[i-1].T
P_predict = A * P * A.T + Q # 估算状态误差协方差
# 校正
K = P_predict * H.T / (H * P_predict * H.T + R) # 更新卡尔曼增益
X = X_predict + K * (Z.T[i].T - H * X_predict) # 更新预测优化值
P = (np.eye(xr) - K * H) * P_predict # 更新状态误差协方差
# 记录系统的预测优化值
for j in range(xr):
X_mat[j, i] = X[j, 0]
Z_mat = H * X_mat
return Z_mat
kf=Kalmanfilter(x)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置正常显示中文
plt.plot(t,np.array(kf)[0], "g", label='预测优化值')
plt.plot(t,np.array(x[0])[0], "r--", label='测量值')
plt.xlabel("时间") # 设置X轴的名字
plt.ylabel("位移") # 设置Y轴的名字
plt.title("卡尔曼滤波示意图") # 设置标题
plt.legend() # 设置图例
plt.show() # 显示图表在合适的协方差矩阵大小设置之下,卡尔曼滤波算法可得到需要的降噪效果,美!!