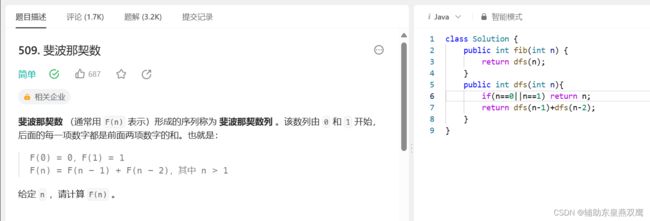
解法1:当然可以冒泡排序,时间复杂度O(n2n^2n2)解法2:单指针循环两次,第一次循环将所有的0交换到前面;第二次循环将所有的1交换到0的后面classSolution{publicvoidsortColorsBySinglePointer(int[]nums){intzeroCnt=0,p=0;for(inti=0;i
决策树算法全解析:从零基础到Titanic实战,一文搞定机器学习经典模型
吴师兄大模型
0基础实现机器学习入门到精通算法机器学习决策树人工智能深度学习编程开发语言
Langchain系列文章目录01-玩转LangChain:从模型调用到Prompt模板与输出解析的完整指南02-玩转LangChainMemory模块:四种记忆类型详解及应用场景全覆盖03-全面掌握LangChain:从核心链条构建到动态任务分配的实战指南04-玩转LangChain:从文档加载到高效问答系统构建的全程实战05-玩转LangChain:深度评估问答系统的三种高效方法(示例生成、手
基于Docker 搭建Redis三主三从分布式集群
DBA学习之路
dockerredis容器
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、分布式系统规划二、准备配置文件1.创建redis集群目录三、启动Redis容器四、创建分布式系统1.创建集群2.查看节点信息总结前言提示:这里可以添加本文要记录的大概内容:本次搭建的为”三主三从“的分布式系统,分布式系统中节点存放的数据可以是不同的。当有数据写入请求到达分布式系统后,系统会采用虚拟槽分区算法将数据写入相
TikTokenizer 开源项目教程
邱纳巧Gillian
TikTokenizer开源项目教程tiktokenizerOnlineplaygroundforOpenAPItokenizers项目地址:https://gitcode.com/gh_mirrors/ti/tiktokenizer项目介绍TikTokenizer是一个基于Python的开源项目,旨在提供一个高效、灵活的文本分词工具。该项目利用先进的算法和数据结构,能够快速准确地对文本进行分词处
洛谷P2678[NOIP2015]跳石头(二分算法)
猪猪成
C++笔记洛谷算法c++
题目:AC通过图如下简短的AC代码如下:#include#includeusingnamespacestd;intmain(){intl,n,m;cin>>l>>n>>m;intarr[50001];intnow,left,right,mid;left=0;right=l;//给2位置变量初始化数值;for(inti=1;i>arr[i];}arr[0]=0;intsum;//记录搬走的石块总和;
宇树科技纯技能要求总结
极梦网络无忧
杂谈科技
一、嵌入式开发与硬件设计核心技能嵌入式开发:精通C/C++,熟悉STM32、ARM开发熟悉LinuxBSP开发及驱动框架(SPI/UART/USB/FLASH/Camera/GPS/LCD)掌握主流平台(英伟达、全志、瑞芯微等)硬件设计:精通数字/模拟电路设计,熟悉PCB绘制工具(Altium等)掌握MOS驱动电路、变压器设计及EMC优化熟悉制板/贴片流程及焊接扩展技能电机控制:熟悉有感FOC算法
深入浅出Java Annotation(元注解和自定义注解)
Josh_Persistence
Java Annotation元注解自定义注解
一、基本概述
Annontation是Java5开始引入的新特征。中文名称一般叫注解。它提供了一种安全的类似注释的机制,用来将任何的信息或元数据(metadata)与程序元素(类、方法、成员变量等)进行关联。
更通俗的意思是为程序的元素(类、方法、成员变量)加上更直观更明了的说明,这些说明信息是与程序的业务逻辑无关,并且是供指定的工具或
mysql优化特定类型的查询
annan211
java工作mysql
本节所介绍的查询优化的技巧都是和特定版本相关的,所以对于未来mysql的版本未必适用。
1 优化count查询
对于count这个函数的网上的大部分资料都是错误的或者是理解的都是一知半解的。在做优化之前我们先来看看
真正的count()函数的作用到底是什么。
count()是一个特殊的函数,有两种非常不同的作用,他可以统计某个列值的数量,也可以统计行数。
在统
MAC下安装多版本JDK和切换几种方式
棋子chessman
jdk
环境:
MAC AIR,OS X 10.10,64位
历史:
过去 Mac 上的 Java 都是由 Apple 自己提供,只支持到 Java 6,并且OS X 10.7 开始系统并不自带(而是可选安装)(原自带的是1.6)。
后来 Apple 加入 OpenJDK 继续支持 Java 6,而 Java 7 将由 Oracle 负责提供。
在终端中输入jav
javaScript (1)
Array_06
JavaScriptjava浏览器
JavaScript
1、运算符
运算符就是完成操作的一系列符号,它有七类: 赋值运算符(=,+=,-=,*=,/=,%=,<<=,>>=,|=,&=)、算术运算符(+,-,*,/,++,--,%)、比较运算符(>,<,<=,>=,==,===,!=,!==)、逻辑运算符(||,&&,!)、条件运算(?:)、位
国内顶级代码分享网站
袁潇含
javajdkoracle.netPHP
现在国内很多开源网站感觉都是为了利益而做的
当然利益是肯定的,否则谁也不会免费的去做网站
&
Elasticsearch、MongoDB和Hadoop比较
随意而生
mongodbhadoop搜索引擎
IT界在过去几年中出现了一个有趣的现象。很多新的技术出现并立即拥抱了“大数据”。稍微老一点的技术也会将大数据添进自己的特性,避免落大部队太远,我们看到了不同技术之间的边际的模糊化。假如你有诸如Elasticsearch或者Solr这样的搜索引擎,它们存储着JSON文档,MongoDB存着JSON文档,或者一堆JSON文档存放在一个Hadoop集群的HDFS中。你可以使用这三种配
mac os 系统科研软件总结
张亚雄
mac os
1.1 Microsoft Office for Mac 2011
大客户版,自行搜索。
1.2 Latex (MacTex):
系统环境:https://tug.org/mactex/
&nb
Maven实战(四)生命周期
AdyZhang
maven
1. 三套生命周期 Maven拥有三套相互独立的生命周期,它们分别为clean,default和site。 每个生命周期包含一些阶段,这些阶段是有顺序的,并且后面的阶段依赖于前面的阶段,用户和Maven最直接的交互方式就是调用这些生命周期阶段。 以clean生命周期为例,它包含的阶段有pre-clean, clean 和 post
Linux下Jenkins迁移
aijuans
Jenkins
1. 将Jenkins程序目录copy过去 源程序在/export/data/tomcatRoot/ofctest-jenkins.jd.com下面 tar -cvzf jenkins.tar.gz ofctest-jenkins.jd.com &
request.getInputStream()只能获取一次的问题
ayaoxinchao
requestInputstream
问题:在使用HTTP协议实现应用间接口通信时,服务端读取客户端请求过来的数据,会用到request.getInputStream(),第一次读取的时候可以读取到数据,但是接下来的读取操作都读取不到数据
原因: 1. 一个InputStream对象在被读取完成后,将无法被再次读取,始终返回-1; 2. InputStream并没有实现reset方法(可以重
数据库SQL优化大总结之 百万级数据库优化方案
BigBird2012
SQL优化
网上关于SQL优化的教程很多,但是比较杂乱。近日有空整理了一下,写出来跟大家分享一下,其中有错误和不足的地方,还请大家纠正补充。
这篇文章我花费了大量的时间查找资料、修改、排版,希望大家阅读之后,感觉好的话推荐给更多的人,让更多的人看到、纠正以及补充。
1.对查询进行优化,要尽量避免全表扫描,首先应考虑在 where 及 order by 涉及的列上建立索引。
2.应尽量避免在 where
jsonObject的使用
bijian1013
javajson
在项目中难免会用java处理json格式的数据,因此封装了一个JSONUtil工具类。
JSONUtil.java
package com.bijian.json.study;
import java.util.ArrayList;
import java.util.Date;
import java.util.HashMap;
[Zookeeper学习笔记之六]Zookeeper源代码分析之Zookeeper.WatchRegistration
bit1129
zookeeper
Zookeeper类是Zookeeper提供给用户访问Zookeeper service的主要API,它包含了如下几个内部类
首先分析它的内部类,从WatchRegistration开始,为指定的znode path注册一个Watcher,
/**
* Register a watcher for a particular p
【Scala十三】Scala核心七:部分应用函数
bit1129
scala
何为部分应用函数?
Partially applied function: A function that’s used in an expression and that misses some of its arguments.For instance, if function f has type Int => Int => Int, then f and f(1) are p
Tomcat Error listenerStart 终极大法
ronin47
tomcat
Tomcat报的错太含糊了,什么错都没报出来,只提示了Error listenerStart。为了调试,我们要获得更详细的日志。可以在WEB-INF/classes目录下新建一个文件叫logging.properties,内容如下
Java代码
handlers = org.apache.juli.FileHandler, java.util.logging.ConsoleHa
不用加减符号实现加减法
BrokenDreams
实现
今天有群友发了一个问题,要求不用加减符号(包括负号)来实现加减法。
分析一下,先看最简单的情况,假设1+1,按二进制算的话结果是10,可以看到从右往左的第一位变为0,第二位由于进位变为1。
读《研磨设计模式》-代码笔记-状态模式-State
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/*
当一个对象的内在状态改变时允许改变其行为,这个对象看起来像是改变了其类
状态模式主要解决的是当控制一个对象状态的条件表达式过于复杂时的情况
把状态的判断逻辑转移到表示不同状态的一系列类中,可以把复杂的判断逻辑简化
如果在
CUDA程序block和thread超出硬件允许值时的异常
cherishLC
CUDA
调用CUDA的核函数时指定block 和 thread大小,该大小可以是dim3类型的(三维数组),只用一维时可以是usigned int型的。
以下程序验证了当block或thread大小超出硬件允许值时会产生异常!!!GPU根本不会执行运算!!!
所以验证结果的正确性很重要!!!
在VS中创建CUDA项目会有一个模板,里面有更详细的状态验证。
以下程序在K5000GPU上跑的。
诡异的超长时间GC问题定位
chenchao051
jvmcmsGChbaseswap
HBase的GC策略采用PawNew+CMS, 这是大众化的配置,ParNew经常会出现停顿时间特别长的情况,有时候甚至长到令人发指的地步,例如请看如下日志:
2012-10-17T05:54:54.293+0800: 739594.224: [GC 739606.508: [ParNew: 996800K->110720K(996800K), 178.8826900 secs] 3700
maven环境快速搭建
daizj
安装mavne环境配置
一 下载maven
安装maven之前,要先安装jdk及配置JAVA_HOME环境变量。这个安装和配置java环境不用多说。
maven下载地址:http://maven.apache.org/download.html,目前最新的是这个apache-maven-3.2.5-bin.zip,然后解压在任意位置,最好地址中不要带中文字符,这个做java 的都知道,地址中出现中文会出现很多
PHP网站安全,避免PHP网站受到攻击的方法
dcj3sjt126com
PHP
对于PHP网站安全主要存在这样几种攻击方式:1、命令注入(Command Injection)2、eval注入(Eval Injection)3、客户端脚本攻击(Script Insertion)4、跨网站脚本攻击(Cross Site Scripting, XSS)5、SQL注入攻击(SQL injection)6、跨网站请求伪造攻击(Cross Site Request Forgerie
yii中给CGridView设置默认的排序根据时间倒序的方法
dcj3sjt126com
GridView
public function searchWithRelated() {
$criteria = new CDbCriteria;
$criteria->together = true; //without th
Java集合对象和数组对象的转换
dyy_gusi
java集合
在开发中,我们经常需要将集合对象(List,Set)转换为数组对象,或者将数组对象转换为集合对象。Java提供了相互转换的工具,但是我们使用的时候需要注意,不能乱用滥用。
1、数组对象转换为集合对象
最暴力的方式是new一个集合对象,然后遍历数组,依次将数组中的元素放入到新的集合中,但是这样做显然过
nginx同一主机部署多个应用
geeksun
nginx
近日有一需求,需要在一台主机上用nginx部署2个php应用,分别是wordpress和wiki,探索了半天,终于部署好了,下面把过程记录下来。
1. 在nginx下创建vhosts目录,用以放置vhost文件。
mkdir vhosts
2. 修改nginx.conf的配置, 在http节点增加下面内容设置,用来包含vhosts里的配置文件
#
ubuntu添加admin权限的用户账号
hongtoushizi
ubuntuuseradd
ubuntu创建账号的方式通常用到两种:useradd 和adduser . 本人尝试了useradd方法,步骤如下:
1:useradd
使用useradd时,如果后面不加任何参数的话,如:sudo useradd sysadm 创建出来的用户将是默认的三无用户:无home directory ,无密码,无系统shell。
顾应该如下操作:
第五章 常用Lua开发库2-JSON库、编码转换、字符串处理
jinnianshilongnian
nginxlua
JSON库
在进行数据传输时JSON格式目前应用广泛,因此从Lua对象与JSON字符串之间相互转换是一个非常常见的功能;目前Lua也有几个JSON库,本人用过cjson、dkjson。其中cjson的语法严格(比如unicode \u0020\u7eaf),要求符合规范否则会解析失败(如\u002),而dkjson相对宽松,当然也可以通过修改cjson的源码来完成
Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解
yaerfeng1989
timerquartz定时器
原创整理不易,转载请注明出处:Spring定时器配置的两种实现方式OpenSymphony Quartz和java Timer详解
代码下载地址:http://www.zuidaima.com/share/1772648445103104.htm
有两种流行Spring定时器配置:Java的Timer类和OpenSymphony的Quartz。
1.Java Timer定时
首先继承jav
Linux下df与du两个命令的差别?
pda158
linux
一、df显示文件系统的使用情况,与du比較,就是更全盘化。 最经常使用的就是 df -T,显示文件系统的使用情况并显示文件系统的类型。 举比例如以下: [root@localhost ~]# df -T Filesystem Type &n
[转]SQLite的工具类 ---- 通过反射把Cursor封装到VO对象
ctfzh
VOandroidsqlite反射Cursor
在写DAO层时,觉得从Cursor里一个一个的取出字段值再装到VO(值对象)里太麻烦了,就写了一个工具类,用到了反射,可以把查询记录的值装到对应的VO里,也可以生成该VO的List。
使用时需要注意:
考虑到Android的性能问题,VO没有使用Setter和Getter,而是直接用public的属性。
表中的字段名需要和VO的属性名一样,要是不一样就得在查询的SQL中
该学习笔记用到的Employee表
vipbooks
oraclesql工作
这是我在学习Oracle是用到的Employee表,在该笔记中用到的就是这张表,大家可以用它来学习和练习。
drop table Employee;
-- 员工信息表
create table Employee(
-- 员工编号
EmpNo number(3) primary key,
-- 姓