【梳理】离散数学 第14章 图的基本概念 14.1 图 14.2 通路与回路

教材：《离散数学》第2版 屈婉玲 耿素云 张立昂 高等教育出版社
源文档高清截图在最后

第14章 图的基本概念

14.1 图

1、图论中的图与几何中的图形有着本质区别。图论重点研究点与点的连线，而与点的具体位置基本无关。

2、设集合A、B，称{{a, b}| a∈A∧b∈B}为A与B的无序积A&B。无序积中的无序对{a, b}也可记作(a, b)，允许a＝b。由于(a, b)＝(b, a)，因此A&B＝B&A。

3、一个无向图G是一个有序二元组，其中
（1）顶点集V是一个非空有穷集，元素称为顶点或节点（结点）。
（2）边集E是无序积V&V的有穷多重子集，元素称为无向边。
如果是有向图，（2）应该改成：边集E是笛卡尔积V×V的有穷多重子集，称作边集，元素称为有向边。

4、多重集合是允许重复元素的集合，一个元素重复出现的次数称为该元素的重复度。一般的集合可以看做所有元素的重复度均为1的多重集。

5、顶点数称为图的阶，含n个顶点的图也叫作n阶图。一条边都没有的图称作零图。n阶零图记作Nn。1阶零图N1称作平凡图，只有一个顶点，没有边。虽然图的定义要求顶点集V非空，但图的运算中可能产生顶点集为空集的结果，称作空图，记作∅。用图形表示图时，如果给全部顶点和边都指定符号（字母、带下标的字母、数字），则称这样的图为标定图，否则称作非标定图。将有向图的各有向边改成无向边后得到的无向图称为这个有向图的基图。

6、设无向图G(V, E)（也记作G＝(V, E)，G＝），ek＝(vi, vj)∈E，则vi, vj为ek的端点，ek与vi, vj关联。若vi≠vj，则称ek与vi, vj的关联次数为1；否则为2，并称ek为环。若e与v不关联，就称e与v的关联次数为0。若无向图的两个顶点vi, vj有一条边连接，就称两个顶点相邻；若两条边至少有一个公共端点，就称两条边相邻。

7、设有向图D(V, E)，ek＝(vi, vj)∈E，则vi, vj为ek的端点，ek与vi, vj关联。vi, vj分别是ek的始点（起点）、终点。若vi＝vj，则称ek为环。若有向图的两个顶点vi, vj有一条有向边连接，就称两个顶点相邻；若两条边中一条边的终点是另一条边的起点，就称两条边相邻。

8、有向图和无向图中，没有边关联的顶点称为孤立点。

9、设无向图G(V, E)，v∈V，则NG(v)＝{u | u∈V∧(u, v)∈E∧u≠V}为v的邻域， 为v的闭邻域，称IG(v)＝{e | e∈E∧e与v关联}为v的关联集。可见，无向图中，顶点v的邻域就是与v由一条边直接相连的顶点的集合，关联集就是以v为端点的无向边的集合。

10、设有向图D(V, E)，v∈V，则称 为v的后继元集， 为v的先驱元集，称 为v的邻域，称 为v的闭邻域。

11、无向图中，如果关联一对顶点的无向边多于1条，则称这些边为平行边，平行边的条数称作重数。有向图中，如果关联一对顶点的有向边多于1条且方向相同（起点终点相同），则称这些边为平行边。含平行边的图称作多重图，既不含平行边也不含环的图称作简单图。

12、无向图G(V, E)中，v∈V，称v作为边的端点的次数为v的度数，简称度，记作dG(v)。不混淆时，可以简记为d(v)。有向图D(V, E)中，v∈V，分别称v作为边的始点和终点的次数为出度 和入度 ，简记分别为d+(v)和d-(v)，度数 ，简记为d(v)。无向图中，顶点v上的环以v做两次端点。有向图中，顶点v上的环以v做两次端点（一次起点和一次终点）。

13、无向图G(V, E)中，Δ(G) = max(d(v) | v∈V)，δ(G)＝min(d(v) | v∈V)分别称为G的最大度和最小度。类似地，定义有向图D(V’, E’)的最大度、最小度、最大出度、最小出度、最大入度、最小入度分别为：
Δ(D)＝max(d(v) | v∈V’)，δ(D)＝min(d(v) | v∈V’)，Δ+(D)＝max(d+(v) | v∈V’)，δ+(D)＝min(d+(v) | v∈V’)，
Δ-(D)＝max(d-(v) | v∈V’)，δ-(D)＝min(d-(v) | v∈V’)。
度数为1的顶点为悬挂顶点，与其关联的边称作悬挂边。度为偶数（奇数）的顶点称为偶度（奇度）顶点。

14、握手定理（1） 无向图的所有顶点的度数之和等于边数的两倍。（有n个人握手，每人握手x次，握手总次数为S = nx/2）
证明 无向图的每条边都为两个顶点（可以是同一个）提供1个入度和1个出度，如果共有|E|条边，就提供2|E|度。

15、握手定理（2） 有向图的所有顶点的度数之和等于变数的两倍。所有顶点的入度之和等于出度之和，都等于边数。
证明 略
推论 任何图中奇度顶点的个数是偶数。
证明 设图G(V, E)，记V1＝{v | v∈V∧d(v)为奇数}，V2＝{v | v∈V∧d(v)为偶数}，则V1∪V2＝V，V1∩V2＝∅。由握手定理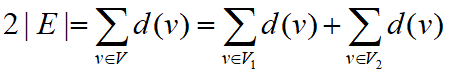， 。而2|E|是偶数， 也是偶数（每个偶度顶点都提供2个度），所以 也为偶数。但奇度顶点只提供奇数个度，而奇数＋奇数＝偶数，所以奇度顶点的数量只能是偶数。

16、设n阶无向图G(V, E)，V＝{v1，v2，……，vn}。称d(v1)，d(v2)，……d(vn)为G的度数列。对顶点标定的无向图，度数列唯一。反之，若给定非负整数列d = d1，d2，……dn，如果存在一个以V＝{v1，v2，……，vn}为顶点集的无向图G，使d(vi) = di，就说数列d是可图化的。如果得到的图是简单图，就说d是可简单图化的。对有向图可以类似定义出度列和入度列。

17、非负整数列d = d1，d2，……dn可图化当且仅当 为偶数。
证明 由握手定理，必要性（左推右）显然。
充分性（右推左）。 为偶数，但奇数＋奇数＝偶数，偶数＋偶数＝偶数，所以数列d一定有2k（0≤k≤floor(n / 2)）个奇数，记为d1，d2，……d2k。可以构造一个以d为度数列的n阶无向图G(V, E)：V＝{v1，v2，……，vn}，在顶点vr与vr+k之间连边，r = 1，2，……，k，共k条边。构造一个新的数列d’ = d1’，d2’，……dn’，若某项di为偶数，则di’ = di；否则di’ = di－1。在顶点vi处画di’ / 2条环，构成无向图G(V, E)。当然，能够构造的图不唯一。

18、设G为任意n阶简单无向图，则Δ(G)≤n－1。因为没有重边和环时，最极端的情况是每个顶点都跟其它n－1个顶点各连1条边。

19、回忆：9.2 代数系统
同构 设同类型的代数系统A1 = ，A2 = 。并记f：A→B。 x、y∈A都有f(x ▫ y) = f(x) * f(y) ，就称f是A1到A2的同态映射，简称同态。f为单射、双射、满射（一一映射）函数时，同态分别具体地说成单同态、满同态、同构。f为满同态时，称A2是A1的同态像，记作A1 ~ A2；f为同构时，也称A1同构于A2，记作A1 A2。
如果同态映射f是从代数系统V到V本身的，就称f为自同态。类似地可以定义单自同态、满自同态、自同构。
等价类 设R为非空集合A上的等价关系，任意x∈A，令[x]R = {y | y∈A∧xRy}，则称[x]R为x关于R的等价类，简称x的等价类。x的等价类是A中所有与x等价的元素构成的集合。
设图（无向或有向）G1(V1, E1)，G2(V2, E2)，若存在双射函数f：→，使得对任意vi, vj∈V1，(vi, vj)∈E1当且仅当(f(vi), f(vj))∈E2，且(vi, vj)与(f(vi), f(vj))的重数相同，就称G1与G2同构。
图之间的同构关系构成全体图集合上的二元关系，它是等价关系：具有自反性、对称性、传递性。根据同构关系构成的等价类中的全部图在同构意义下可以看成同一个图（同一类图）。至今还没有找到判断两个图是否同构的便于检查的充要条件。阶数、边数、度数相同都是同构的必要条件（右推左），但都不是充分条件。度数列相同的两个图也可以不同构。

20、设n阶无向简单图G，G中的每个顶点均与其它n－1个顶点相邻，则称G为n阶无向完全图，简称n阶完全图，记作Kn（n≥1）。设n阶有向简单图D，D中的每个顶点均邻接到其它n－1个顶点，则称D为n阶有向完全图。设D为n阶有向简单图（不一定是n阶有向完全图），若D的基图（有向边全部改成无向边后的图）为n阶无向完全图，就称D为n阶竞赛图。

21、设G为n阶无向简单图，若对任意v∈V(G)，均有d(v) = k，就称G为k-正则图。
n阶零图是0-正则图，n阶无向完全图是（n－1）-正则图。彼得森（Peterson）图是3-正则图。由握手定理，n阶k-正则图中，边数m＝kn / 2。因此k为奇数时n必为偶数。

（彼得森图不是平面图，其同构图有120多种。左上角的画法是最常见的画法。）

22、设图G(V, E)和G’(V’, E’)（同为无向或有向），若 ，则称G’是G的子图，G为G’的母图，记作 。当 ，就说G’是G的真子图；若 ，就说G’是G的生成子图。设 且V≠∅，称以V’’为顶点集，以G中两个端点都在V’’中的边组成的集合作为边集E’’的图G[V’’]为G的V’’导出的子图；设 且E’’≠∅，成以E’’为边集，以E’’中的边关联的顶点组成的集合作为顶点集的图G[E’’]称为E’’导出的子图。

23、设n阶无向简单图G(V, E)，设 ，则G’(V, E’)为G的补图。若G与补图G’同构，就说G为自补图。

14.2 通路与回路

1、设G为无向标定图（允许有重边），G中顶点与边的交替序列Γ = vi0ej1vi1ej2…ejlvil称作vi0到vil的通路，与每一条边ej相邻的顶点称为端点，vi0和vil分别称为Γ的起点和终点，Γ中边的条数称为长度。如果始点和终点相同，Γ称为回路。如果Γ的边各异而起点终点不同，称Γ为简单通路；如又有起点终点相同，称Γ为简单回路。如果Γ的顶点各异且边各异，称Γ为初级通路或路径；如又有起点终点相同，称Γ为初级回路或圈。长度为奇数和偶数的圈分别叫作奇圈和偶圈。如果Γ中有重复出现的边，就称Γ为复杂通路；如又有起点终点相同，称Γ为复杂回路。
在有向图中，通路、回路的分类和定义很类似，但要注意有向边方向的一致性。根据定义，初级通路（回路）一定是简单通路（回路），但反之不真。在简单通路（回路）中，可以通过不同的边多次经过同一个顶点，而在初级通路（回路）中则不可以。“重边”和“重复出现的边”不是同一个概念。“重边”指的是连接两个顶点的多条边（平行边），这些边不一定是完全相同的。

2、简单无向图中，圈的长度至少为3；长为1和2的圈分别只能由环和平行边生成。实际情况下，初级通路一般都指起点和终点不相同的通路。

3、在n阶图G中，若顶点u到不同顶点v存在通路，则u到v存在长度≤n－1的通路。
证明 设该通路为Γ = vi0ej1vi1ej2…ejlvil。当其长度l≤n－1时定理成立。当l > n－1时，Γ包含的顶点数大于G的顶点数，于是必定存在k，s使得0≤k < s≤l使得vs = vk。即在Γ上存在vk到自身的回路C。显然这段回路在Γ中是连续的。在Γ上删除C的起点vk以外的点和边，得到Γ’ = vi0ej1vi1ej2…vkes+1…ejlvil。Γ’仍是u到v的通路，且长度至少比Γ少1。若仍不满足要求，重复上述过程。由于G是有限图，每次删掉回路（注意要保留回路的起点）都会令长度减少，所以经过有限步以后必定得到u到v的长度≤n－1的通路。
推论 在n阶图G中，若顶点u到不同顶点v存在通路，则u到v一定存在长度≤n－1的初级通路（路径）。

4、在n阶图G中，若存在v到自身的回路，则一定存在v到自身长度≤n的回路。
推论 在n阶图G中，若存在v到自身的简单回路，则一定存在v到自身长度≤n的初级回路。
证明方法同上。

5、长度相同的圈都是同构的，因此同构意义下给定长度的圈只有一个。标定图中，圈表示成顶点和边的标记序列。只要两个标记序列不同，即使圈的长度相同，也认为两个圈不同，称这两个圈在定义意义下不同。