＜数据结构＞NO5.栈和队列

目录

栈

Ⅰ.栈的概念

Ⅱ.栈的实现

Ⅲ.测试代码

队列

Ⅰ.队列的概念

Ⅱ.队列的实现

---

前言

栈和队列也是一种常见的线性存储的数据结构，只不过它们的某些操作受到了限制，比如栈只允许从栈顶插入删除元素、队列只允许从队尾插入元素，对头删除元素。❗注意：这里的栈数据结构和内存中的栈区没有直接关系！下面我们开始学习栈和队列吧~

ps:完整代码在

栈

Ⅰ.栈的概念

栈的定义：栈是一种特殊的线性表，只允许在固定的一端进行插入和删除元素、只能访问栈顶元素。进行插入和删除的那一端称为栈顶。

栈的操作：
①push：从栈顶插入元素。
②pop：从栈顶删除元素。
③top：获取栈顶元素。
④size：获取栈中元素个数。
⑤empty：判断是否为空栈。
⑥init：初始化栈。
⑦destroy：销毁栈。

❗注意：由于栈的结构规定，每次只能访问栈顶元素，所以不能定义函数能一次将栈所有元素打印出来。

 

Ⅱ.栈的实现

❓请思考：栈的实现可以由哪些结构完成？数组还是链表？
答案：栈更适合用数组实现。 解析：栈中插入删除元素的方向是固定的，即只能从栈顶插入、删除元素，所以我们可以将数组尾部定义为栈顶，这样每次插入删除元素只需要对数组尾部元素进行操作，这样的插入、删除的时间复杂度O(1)但是相比链表缓存命中率更高、效率更高。

通过数组实现的栈和顺序表的实现类似，无非就是栈相比顺序表的定义限制了插入、删除的操作。
❗注意：顺序表中的有效成员个数在栈中替换成了栈顶top成员，top成员指向栈顶元素的后一个元素(也可以指向栈顶元素)。

 0x01.栈的结构定义 

typedef int STDataType;
typedef struct
{
	STDataType* a;//a指向一个连续的数组
	int top;//top记录栈顶后一个元素的下标
	int capacity;
}Stack;

 0x02.栈的初始化

//栈的初始化
void StackInit(Stack* ps)
{
	assert(ps);
	ps->capacity = 0;
	ps->top = 0;//top初始化为0表示空栈
	ps->a = NULL;
}

❗注意：如果top表示栈顶元素下一个元素的下标，那么top应初始化为0，因为空栈时没有有效元素；如果top表示栈顶元素的下标，那么top应该初始化为-1,这样栈有一个元素时top才为0。

 0x03.入栈

//入栈
void StackPush(Stack* ps, STDataType x)
{
	assert(ps);
	if (ps->capacity == ps->top)//栈满扩容
	{
		ps->capacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		//realloc可以解决扩容空栈
		STDataType* tmp = realloc(ps->a, sizeof(STDataType) * (ps->capacity));
        //成功开辟了空间在复制
		if (NULL == tmp)
        {
            free(ps->a);
            exit(0);
        }
		ps->a = tmp;
		assert(ps->a);
	}
	ps->a[ps->top] = x;
	ps->top++;
}

0x04.出栈

//出栈
void StackPop(Stack* ps)
{
	assert(ps);
	//空栈不能删除
	assert(!StackEmpty(ps));
	ps->top--;
}

0x05.判断是否空栈

//空栈
bool StackEmpty(const Stack* ps)
{
	return ps->top == 0;
}

❗注意：判断为空栈必须封装成一个函数，因为使用者不清楚top是栈顶元素下标还是栈顶下一个元素下标。所以无法通过top==0判断是否为空栈。

0x06.获取栈顶元素

//获取栈顶元素
STDataType StackTop(const Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top - 1];//top是指向栈顶下一个元素
}

❗注意：获取栈顶元素也需要封装成一个函数，因为使用者不知道top是指向栈顶还是栈顶下一个元素。

0x07.获取栈元素个数

//获取栈元素个数
int StackSize(const Stack* ps)
{
	assert(ps);
	return ps->top;
}

0x08.销毁栈

//销毁栈
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->a);
	ps->capacity = ps->top = 0;
}

Ⅲ.测试代码

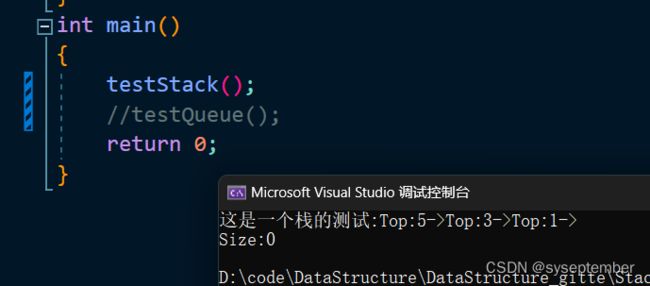
void testStack()
{
    printf("这是一个栈的测试:");
	Stack ps;
	assert(&ps);
	StackInit(&ps);
	StackPush(&ps, 1);
	StackPush(&ps, 2);
	StackPop(&ps);
	StackPush(&ps, 3);
	StackPush(&ps, 4);
	StackPop(&ps);
	StackPush(&ps, 5);
	while (!StackEmpty(&ps))
	{
		printf("Top:%d->", StackTop(&ps));
		StackPop(&ps);
	}
	printf("\nSize:%d\n", StackSize(&ps));
	StackDestroy(&ps);
}

运行代码：

---

队列

Ⅰ.队列的概念

队列的定义：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出 FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾 出队列：进行删除操作的一端称为队头。

队列的操作：和栈类似，这里多实现一个获取队尾元素(与STL标准库队列操作保持一致)
①push：从队尾插入元素。
②pop：从队头删除元素。
③front：获取对头元素。
④back：获取队尾元素。
⑤empty：判断是否为空栈。
⑥init：初始化栈。
⑦destroy：销毁栈。
⑧size：获取队列元素个数

Ⅱ.队列的实现

❓请思考：队列是通过数组还是链表来实现？
答案：通过链表实现更好。解析： 如果通过数组实现，如果数组首元素是队列头，那么每次队列删除元素时数组需要挪动数据；如果数组尾元素是队列头，那么每次队列插入数据时数组都需要挪动数据，时间复杂度为O(n); 如果通过链表实现，那么插入删除都只需要O(1)的时间复杂度即可完成。

❓请思考：队列的结构定义应该是怎样的？
答案：队列的定义包含队列头节点指针、队列尾节点指针、队列元素个数三个成员。而队列是通过链表实现的，所以队列节点成员也应该是一个结构体，包含数据与和指针域。
 

0x01.队列的结构定义
 

typedef int QDataType;
//队列由于具备先进后出的特点，使用链表实现效率更高，因为数组头插和头删的效率比链表低
typedef struct Qnode
{
	QDataType val;
	struct Qnode* next;
}Qnode;
typedef struct
{
	Qnode* head;//指向队列头
	Qnode* tail;//指向队列尾
	int size;//记录队列有效元素个数
}Queue;

0x02.队列的初始化

//队列的初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}

0x03.队列是否为空

//队列是否为空
bool QueueEmpty(const Queue* pq)
{
	assert(pq);
	//return pq->head == NULL && pq->tail == NULL;
	return pq->size == 0;
}

0x04.入队列

//入队列
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	//创建新节点
	Qnode* newnode = (Qnode*)malloc(sizeof(Qnode));
	assert(newnode);
	newnode->val = x;
	newnode->next = NULL;
	//链表为空
	if (pq->tail == NULL)
	{
		assert(pq->head == NULL);//链表为空尾指针一定为空
		pq->head = pq->tail = newnode;
	}
	else
	{
		//直接尾插
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
	pq->size++；
}

❗注意：入队列本质上是对链表进行尾插，如果链表为空时插入节点需要让尾指针和头指针都指向该节点。

0x05.出队列

//出队列
void QueuePop(Queue* pq)
{
	assert(pq);
	//空队列不能删除
	assert(!QueueEmpty(pq));
	//只有1个节点
	if (pq->size == 1)
	{
		Qnode* tmp = pq->head;
		pq->head = pq->tail = NULL;
		free(tmp);
	}
	//2节点及以上
	else
	{
		//头删
		Qnode* tmp = pq->head;
		pq->head = pq->head->next;
		free(tmp);
	}
	pq->size--;
}

❗注意：出队列本质是对列表进行头删，所以需要分链表为空、一个节点、多个节点进行讨论，一个节点是需要将头尾指针都置空。

0x06.获取队列头

//获取队列头部元素
QDataType QueueFront(const Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->val;
}

0x07.获取队列尾

//获取队列尾部元素
QDataType QueueBack(const Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->val;
}

0x08.销毁队列

//销毁队列
void QueueDestroy(Queue* pq)
{
	assert(pq);
	Qnode* cur = pq->head;
	while (cur)
	{
		Qnode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = 0;
	pq->size = 0;
}

Ⅲ.测试代码 

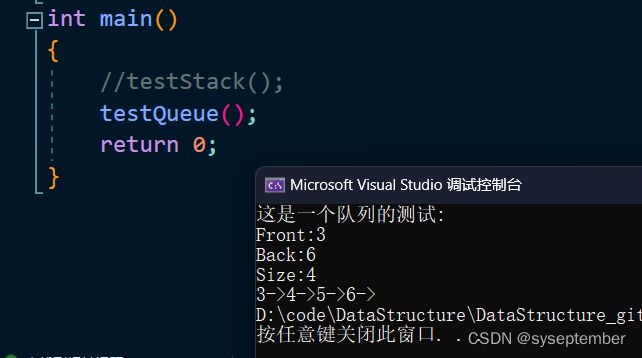
void testQueue()
{
	printf("这是一个队列的测试:");
	Queue pq;
	assert(&pq);
	QueueInit(&pq);
	QueuePush(&pq, 1);
	QueuePush(&pq, 2);
	QueuePush(&pq, 3);
	QueuePush(&pq, 4);
	QueuePush(&pq, 5);
	QueuePush(&pq, 6);
	QueuePop(&pq);
	QueuePop(&pq);
	printf("Front:%d\n", QueueFront(&pq));
	printf("Back:%d\n", QueueBack(&pq));
	printf("Size:%d\n", QueueSize(&pq));
	while (!QueueEmpty(&pq))
	{
		printf("%d->", QueueFront(&pq));
		QueuePop(&pq);
	}
	QueueDestroy(&pq);
}

运行代码：

---