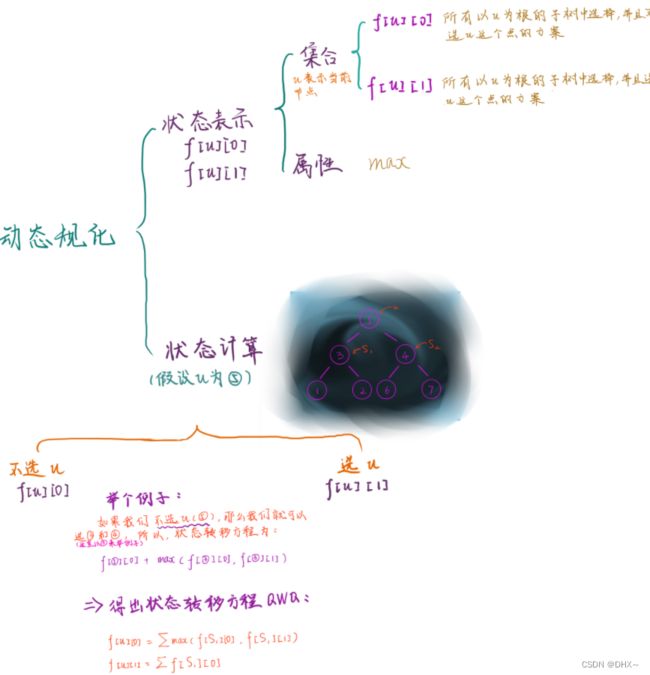
树形DP()
没有上司的舞会
Ural 大学有 N 名职员,编号为 1∼N。
他们的关系就像一棵以校长为根的树,父节点就是子节点的直接上司。
每个职员有一个快乐指数,用整数 Hi 给出,其中 1≤i≤N。
现在要召开一场周年庆宴会,不过,没有职员愿意和直接上司一起参会。
在满足这个条件的前提下,主办方希望邀请一部分职员参会,使得所有参会职员的快乐指数总和最大,求这个最大值。
输入格式
第一行一个整数 N。
接下来 N 行,第 i 行表示 i 号职员的快乐指数 Hi。
接下来 N−1 行,每行输入一对整数 L,K,表示 K 是 L 的直接上司。(注意一下,后一个数是前一个数的父节点,不要搞反)。
输出格式
输出最大的快乐指数。
数据范围
1≤N≤6000
−128≤Hi≤127
输入样例:
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
输出样例:
5
#include
#include
#include
using namespace std;
const int N=6100;
int h[N],ne[N],e[N],idx;
int happy[N];
bool has_father[N];
int f[N][2];
bool st[N];
int root=1;
//建表
void add(int a,int b)
{
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
void dfs(int u)
{
f[u][1]=happy[u];//如果选当前节点u,就可以把f[u,1]先怼上他的高兴度
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
dfs(j);
//状态转移部分
f[u][0]+=max(f[j][1],f[j][0]);
f[u][1]+=f[j][0];
}
}
int main()
{
int n;cin>>n;
for(int i=1;i<=n;i++) cin>>happy[i];
memset(h,-1,sizeof h);
for(int i=1;i>a>>b;
add(b,a);
//若有父节点标记一下
has_father[a]=true;
}
//找树根 树根没有父节点
while(has_father[root]) root++;
dfs(root);
cout< 树的最长路径
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示树的最长路径的长度。
数据范围
1≤n≤10000
1≤ai,bi≤n
−105≤ci≤105
输入样例:
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
输出样例:
22
#include
#include
#include
using namespace std;
const int N=2e5+10;
int h[N],ne[N],w[N],e[N],idx;
int n;
int ans=0;
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
//father表示u的父节点,因为该图为无向图,并且迭代过程中不能回到父节点,所以要特殊标记.
int dfs(int u,int father)
{
//因为题目描述中有:注意:路径中可以只包含一个点
//所以题目中的结果一定不为负数,负的路径由此可以忽略掉
int d1=0,d2=0;
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(j==father) continue;
int d=dfs(j,u)+w[i];//求出路径的长度
if(d>=d1) d2=d1,d1=d; //d1,d2求出以该点为顶点的最长路径
else if(d>d2) d2=d;//最长路径和次长路径
}
ans=max(ans,d1+d2);
return d1;
}
int main()
{
cin>>n;
memset(h,-1,sizeof h);
for(int i=1;i>a>>b>>c;
add(a,b,c);
add(b,a,c);
}
dfs(1,-1);
cout< D. Apple Tree
蒂莫菲的花园里长着一棵苹果树;它是n个顶点的有根树,根在顶点1中(顶点编号从1到n)。树是一个没有循环和多条边的连通图。这棵树很不寻常,它的根向上生长。然而,对于程序员的树来说,这是很正常的。苹果树很年轻,所以上面只会长两个苹果。苹果会生长在某些顶点(这些顶点可能是相同的)。苹果长出来后,蒂莫菲开始摇晃苹果树,直到苹果掉下来。每次Timofey摇动苹果树时,每个苹果都会发生以下情况:让苹果现在位于顶点u。如果一个顶点u有一个子顶点,苹果就会移动到它上面(如果有几个这样的顶点,苹果可以移动到其中的任何一个)。否则,苹果就会从树上掉下来。可以看出,在有限的时间后,两个苹果都会从树上掉下来。Timofey有苹果可以生长的顶点的q假设。他假设苹果可以在顶点xyy中生长,并想知道苹果可以从树上掉落的顶点对(a,b)的数量,其中a——从顶点x掉落的苹果将从顶点掉落,b——从顶点yy掉落的苹果。帮他做这个。 (多组输入 并且1时根节点)
输入样例
2
5
1 2
3 4
5 3
3 2
4
3 4
5 1
4 4
1 3
3
1 2
1 3
3
1 1
2 3
3 1
输出样例
2 2 1 4 4 1 2
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=5e5+10;
int h[N],ne[N],e[N],idx,w[N];
int cnt[N];
int n;
void add(int a,int b)
{
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
void dfs(int u,int father)
{
if(w[u]==1&&u!=1)
{
cnt[u]=1;
return ;
}
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(father==j) continue;
dfs(j,u);
cnt[u]+=cnt[j];
}
}
int main()
{
int t;cin>>t;
while(t--)
{
cin>>n;
memset(h,-1,sizeof 4*(n+1));
memset(cnt,0,sizeof 4*(n+1));
memset(w,0,sizeof 4*(n+1));
for(int i=1;i>a>>b;
add(a,b);
add(b,a);
w[a]++;
w[b]++;
}
dfs(1,-1);
int q;
cin>>q;
while(q--)
{
int a,b;cin>>a>>b;
cout<<(ll)cnt[a]*cnt[b]<