强化学习-理解及应用:解决迷宫问题
什么是强化学习?
强化学习(Reinforcement Learning, RL)是一种机器学习方法,旨在让智能体(agent)通过与环境的交互学习如何做出最优的行动选择以获得最大的累积奖励。
7个基本概念
强化学习主要由智能体(Agent)、环境(Environment)、状态(State)、动作(Action)、奖励(Reward)、策略(policy)、价值函数(Value)组成。
在强化学习中,智能体需要在不断尝试和错误的过程中学习,通过观察环境的反馈(奖励或惩罚)来调整自己的行为,从而逐步改进策略。
如何理解呢?看那么多概念,一般不好理解,咱们举例说明:迷宫游戏。
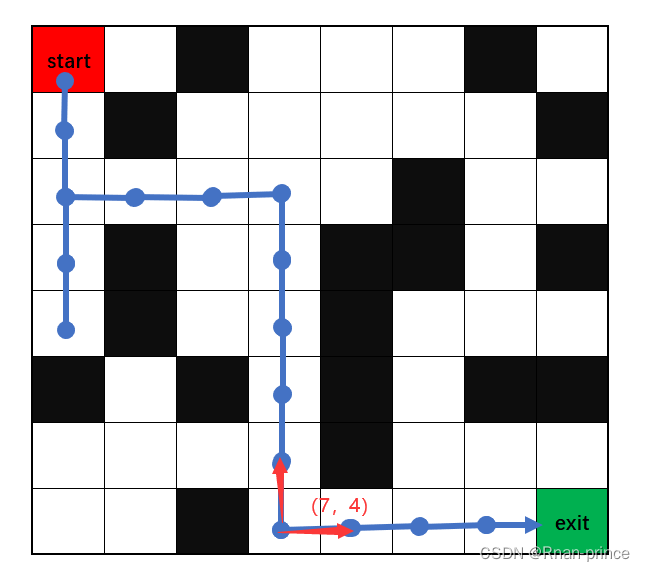
迷宫与图中类似,黑色格子为墙,不能走,老鼠试图走向墙时,会停在原地。白色格子为空地,可以走。蓝点表示走过的宫格。起始位置为左上角,结束位置为右下角。
1、智能体
红start表示智能体,它在迷宫这个环境中玩耍:
强化学习的目标就是让红点变得足够智能,智能到什么程度呢?让它能够顺利的找到从start(起始点)到exit(出口)的路径,并且学习到最后:让它能够从任意一个起始点找到一条合适的路径从出口出去。
2、环境
在这里就是迷宫,迷宫环境里有:初始出发点,白色方块表示可以通行的格子,黑色格子表示障碍物,绿点表示迷宫出口,迷宫的长为8个格子,宽为8个格子,这些元素组成了强化学习的环境。
3、状态
这个对于初学者觉得会比较抽象,在迷宫游戏里,状态可以理解为红点所在的一个格子里
8×8的宫格,左上角为起始点,行标号为0-7,列标号为0-7,假定智能体走到了箭头所指的红点,那么此时智能体的状态可以抽象为 (7,4)
4、动作
动作是智能体在特定状态下可以执行的操作。它可以是离散的(例如,向左/向右)或连续的(例如,控制机器臂的力或位置)。
在迷宫游戏里,智能体状态为 (7,4) 时,它可能的动作只有两个:向上和向右,如图2个红色箭头所示,动作取值是离散的。
5、奖励
奖励是环境针对智能体的行为给出的反馈信号。它用来评估智能体的行为好坏,并作为学习信号指导智能体的决策。
在迷宫游戏中,如果智能体已经当前状态为 (7,4) ,并且它的上一个状态为 (6,4) ,因为此时它有两个动作选择,向上或向右。
如果它动作向上,表明重复原来路径,我们要给它一个惩罚奖励,尽量让它不要重复走路;相反,如果向右走,我们给它一个相对于向上来说更好的奖励,因此,这就让智能体更倾向选择向右走了。
6、策略
策略定义了智能体在给定状态下选择动作的方式。这个概念也是比较抽象的,策略到底是什么意思?
举一个常用到的策略:ε-贪婪策略(ε-greedy)。
该策略在选择动作时,以1-ε的概率选择当前最优的动作,以ε的概率选择随机动作。也就是说,在智能体当前状态为 (7,4) 时,下一状态它有可能再向上移动,尽管在当前这个环境下,向上移动我们直接观察出并不明智。但是,对于其他情况,随机选择动作会有可能得到意想不到的好结果。
详细算法将在下一节中(xxx)讲到.。
7、值函数
值函数用来评估状态或状态-动作对的价值,表示从该状态或状态-动作对开始,智能体能够获得的长期累积奖励的期望值。
更加通俗来说,值函数就是给你智能体的一个状态,返回它的累计奖励值。可以使用深度学习网络模型来逼近值函数,比如:让神经网络输入状态,输出各个动作下的奖励值。
详细算法将在下一节中(xxx)讲到。
马尔科夫决策过程
马尔科夫决策过程(Markov Decision Process,MDP),MDP提供了描述序贯决策问题的数学框架,是强化学习的基础之一。
它将决策问题建模为:状态、动作、转移概率和奖励的组合,并通过优化累积奖励的目标来找到最优的决策策略。
MDP包含以下要素:
- 状态(State):系统或环境可能处于的不同状态。
- 动作(Action):在每个状态下可选的决策或行动。
- 转移概率(Transition Probability):在执行某个动作后,系统从一个状态转移到另一个状态的概率分布。
- 奖励(Reward):在每个状态执行某个动作后获得的即时奖励。
- 策略(Policy):根据当前状态选择动作的策略。
我们依然通过迷宫问题来理解。
1、状态(State)
在这个例子中,状态是智能体所处的位置坐标,即迷宫中的某个格子。例如,可以使用(x, y)坐标来表示状态,其中x和y是迷宫中某个格子的行和列索引。
状态可以表示为一个二维坐标 (x, y),其中 x 表示迷宫的行索引,y 表示迷宫的列索引。假设迷宫的大小为 N × M,则状态集合为:
![]()
2、动作(Action)
动作是智能体在某个状态下可以采取的行动,即向上、向下、向左或向右移动。可以使用符号(u,d,l,r)来表示相应的动作。
3、转移概率(Transition Probability)
转移概率描述在某个状态下执行某个动作后,智能体转移到下一个状态的概率分布。
在迷宫游戏中,转移概率是确定性的,因为智能体在执行一个动作后会准确地移动到下一个状态。例如,如果智能体在状态(x, y)执行向上的动作,那么下一个状态将是(x, y-1),转移概率为1。
由于在迷宫中移动是确定性的,转移概率可以表示为函数
![]()
其中![]() 表示在状态
表示在状态 s 下执行动作 a 后转移到状态 s' 的概率。
根据迷宫规则,如果智能体在状态 执行动作 a,那么下一个状态 s' 可以根据动作 a 来计算,例如:
- 如果
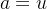 ,则
,则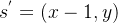
- 如果
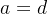 ,则
,则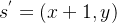
- 如果
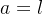 ,则
,则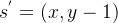
- 如果
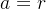 ,则
,则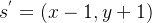
其中,在边界情况下,如果智能体试图移动到迷宫之外的位置或者移动到墙壁位置,转移概率为0。
4、奖励(Reward)
奖励是智能体在执行某个动作后所获得的即时反馈。
在迷宫游戏中,可以设置以下奖励机制:
- 当智能体移动到宝藏位置时,获得正奖励(例如+10)。
- 当智能体移动到墙壁位置时,获得负奖励(例如-20)。
- 在其他情况下,获得较小的负值奖励(例如-0.01),以鼓励尽快找到宝藏。
奖励函数可以表示为函数 :
![]()
其中![]() 表示在状态
表示在状态 s 下执行动作 a 后转移到状态 s' 的即时奖励。
根据迷宫的设定,定义如下奖励:
-
如果s'是宝藏位置,则
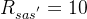
-
如果s'是墙壁位置,则
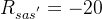
-
否则,
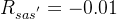
策略迭代
策略迭代是马尔可夫决策过程(MDP)中的一种求解方法,也是强化学习常用求解方法。
依然以迷宫游戏为例,目标是找到迷宫的出口。你每到达一个迷宫的某个位置,都需要根据当前的状态(位置)来选择一个行动(向上、向下、向左、向右)来移动。
你希望找到一种“最优的策略”,即在每个位置都选择最好的行动,从而尽快找到迷宫的出口。策略迭代的思想也非常直接,就是通过不断“改进策略”来寻找最优策略。所以策略迭代主要分为两个步骤:策略评估和策略改进。
策略评估
对当前的策略进行评估,计算每个状态的值函数(表示在该状态下能够获得的预期累积奖励)。通过迭代计算每个状态的值函数,直到值函数收敛。
可能不好理解,我们以宫格游戏为例理解:
定义迷宫状态空间大小和动作空间大小分别为64和4,即在8*8的网格中,动作有4种,上下左右。
num_states = 64
num_actions = 4于是就有了策略,一个二维数组,即每一个状态下对应的4种动作的取值概率。
policy = np.ones((num_states, num_actions)) / num_actions
策略迭代方法还有一个值函数,值函数的入参是状态,返回价值大小,初始状态的值大小为0。
values = np.zeros(num_states)
定义迷宫的奖励矩阵:
rewards = np.zeros((8, 8)) - 0.01
rewards[0, 2] = -20
rewards[0, 6] = -20
rewards[1, 1] = -20
rewards[1, 7] = -20
rewards[2, 5] = -20
rewards[3, 1] = -20
rewards[3, 4] = -20
rewards[3, 5] = -20
rewards[3, 7] = -20
rewards[4, 1] = -20
rewards[4, 4] = -20
rewards[5, 0] = -20
rewards[5, 2] = -20
rewards[5, 4] = -20
rewards[5, 6] = -20
rewards[5, 7] = -20
rewards[6, 4] = -20
rewards[7, 2] = -20
rewards[7, 7] = 10所以策略评估的代码为:
def policy_evaluation():
delta = 1e-6 # 停止迭代的阈值
max_iterations = 1000 # 最大迭代次数
for _ in range(max_iterations):
new_values = np.zeros(num_states)
for s in range(num_states):
value = 0
for a in range(num_actions):
next_state = get_next_state(s, a) # 获取下一个状态
value += policy[s][a] * (rewards[s][a] + values[next_state]) # 贝尔曼方程:四种动作的概率值和
new_values[s] = value
if np.max(np.abs(new_values - values)) < delta:
break
values = new_values价值函数计算是贝尔曼方程,贝尔曼方程是动态规划和强化学习中的基本方程,由Richard Bellman提出。
贝尔曼方程表达了状态或状态-动作对的值与按照特定策略获得的预期回报之间的关系。
贝尔曼方程的一般形式如下:
![]()
其中, ![]() 表示状态
表示状态 ![]() 的值函数,即按照某个策略获得的预期回报。
的值函数,即按照某个策略获得的预期回报。 ![]() 表示选择能够使得值最大化的动作
表示选择能够使得值最大化的动作![]() 。
。![]() 表示对所有可能的下一个状态 s' 和奖励 r 进行求和。
表示对所有可能的下一个状态 s' 和奖励 r 进行求和。![]() 表示在状态 s 下执行动作 a 后转移到状态 s' 且获得奖励 r 的概率。
表示在状态 s 下执行动作 a 后转移到状态 s' 且获得奖励 r 的概率。![]() 是折扣因子,用于平衡当前和未来的奖励。
是折扣因子,用于平衡当前和未来的奖励。
策略改进
policy是一个[num_states, num_actions]二维数组,在策略改进这一步实际上就是不断更新每个state下的最优action,就是更新policy二维数组的第二个维度num_actions取值。
伪代码:更新策略 policy 数组
def policy_improvement():
for s in range(num_states):
q_values = np.zeros(num_actions)
for a in range(num_actions):
next_state = get_next_state(s, a) # 获取下一个状态
q_values[a] = rewards[s][a] + values[next_state]
best_action = np.argmax(q_values)
new_policy = np.zeros(num_actions)
new_policy[best_action] = 1
policy[s] = new_policy
联合以上两步就得到策略迭代算法。
def policy_iteration():
max_iterations = 1000 # 最大迭代次数
for _ in range(max_iterations):
policy_evaluation() # 策略评估
policy_improvement() # 策略改进综上,策略迭代是一种通过反复评估和改进策略的方法来求解马尔可夫决策过程的算法。它通过不断优化策略和值函数来找到最优策略,并帮助我们在迷宫游戏等问题中做出最佳的决策。
值迭代
值迭代是强化学习另一种求解方法,用于找到马尔可夫决策过程(MDP)中的最优值函数。
值迭代可以总结为如下几点:
- 值迭代通过不断迭代更新值函数来逼近最优值函数,从而确定最优策略。
- 值迭代的关键是在每次迭代中更新值函数。
- 对于每个状态,通过考虑所有可能的动作和下一个状态,选择能够使值最大化的动作,并计算更新后的值函数。
- 迭代更新值函数,更新公式也是贝尔曼方程,和策略迭代值函数更新公式一样。
- 值迭代需要进行多次迭代,直到值函数收敛为止。收敛时,值函数不再发生显著变化。
因此:值迭代是比策略迭代更为简单的一种迭代方法。
def policy_evaluation():
# 定义参数
gamma = 0.9 # 折扣因子
epsilon = 1e-6 # 收敛阈值
# 初始化价值函数
f_values = np.zeros(grid.shape)
# 动作集合
actions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
# 进行值迭代
while True:
delta = 0
n, m = grid.shape
for i in range(n):
for j in range(m):
if grid[i, j] == -5 or grid[i, j] == 10:
continue
# 计算当前状态的最大价值
max_value = -np.Inf
for x, y in actions:
ni, nj = i + x, j + y
# 边界校验 + 是否是墙校验
if 0 <= ni < grid.shape[0] and 0 <= nj < grid.shape[1] and grid[ni, nj] != -5:
max_value = max(max_value, gamma * f_values[ni, nj])
# 更新价值函数
new_value = grid[i, j] + max_value
delta = max(delta, abs(new_value - f_values[i, j]))
f_values[i, j] = new_value
if delta < epsilon:
break
print(f"最优价值函数:{f_values}")迷宫游戏应用
策略值定义:
策略值是一个表格,用于存储每个状态动作对的估计价值。对于给定的状态
s和动作a,P值表示在状态s执行动作a所获得的长期回报估计。
使用迭代的方式更新P值,通过不断更新policy值来逐步逼近最优策略。更新规则如下:
![]()
其中,![]() 表示在状态
表示在状态 s执行动作 a的值, ![]() 是学习率(0 < α <= 1),r 是执行动作
是学习率(0 < α <= 1),r 是执行动作a后获得的即时奖励,![]() 是折扣因子(0 <=
是折扣因子(0 <=![]() <= 1),
<= 1),![]() 是执行动作
是执行动作a后转移到的下一个状态,![]() 是在下一个状态下选择的动作,
是在下一个状态下选择的动作,![]() 表示在下一个状态
表示在下一个状态![]() 下所有可能动作中选择值最大的动作。
下所有可能动作中选择值最大的动作。
更新规则的含义是,通过将当前P值与新估计的P值加权平均,使P值逐步收敛到最优值。其中,![]() 控制了新估计值的权重, 控制了对未来回报的重视程度。
控制了新估计值的权重, 控制了对未来回报的重视程度。
通过不断地执行更新规则,强化学习算法能够逐步学习到最优的P值,并根据P值选择最佳的动作来达到最优策略。
import numpy as np
def get_possible_actions(row_num, clo_num, row_n, col_n):
target_actions = [0, 1, 2, 3] # 上、下、左、右
if row_num == 0: # 不能向上
target_actions.remove(0)
if clo_num == 0: # 不能向左
target_actions.remove(2)
if row_num == row_n - 1: # 不能向下
target_actions.remove(1)
if clo_num == col_n - 1: # 不能向右
target_actions.remove(3)
return target_actions
def get_next_state(state, action):
row_num, clo_num = state
next_state = state
if action == 0: # 上
next_state = (row_num - 1, clo_num)
elif action == 1: # 下
next_state = (row_num + 1, clo_num)
elif action == 2: # 左
next_state = (row_num, clo_num - 1)
elif action == 3: # 右
next_state = (row_num, clo_num + 1)
return next_state
def get_best_reward_route(grid, begin_cord, exit_coord, max_iterations):
"""
获取最优奖励路径
:param grid: 网格奖励
:param begin_cord: 开始位置
:param exit_coord: 结束位置
:param max_iterations: 最大迭代次数
:return: 最有路径及最大奖励
"""
action_n = 4
row_n, col_n = grid.shape
alpha = 0.1 # 学习率
gamma = 0.9 # 折扣因子
epsilon = 0.3 # ε-greedy策略的ε值
# 初始化策略P表
policy = np.zeros((row_n, col_n, action_n))
best_route = []
max_route_reward = -np.Inf
for n_iter in range(max_iterations):
# 初始化起始位置
state = begin_cord
route = [state]
while state != exit_coord: # 终止条件:到达终点位置
row_num, clo_num = state
# 获取动作集合
possible_actions = get_possible_actions(row_num, clo_num, row_n, col_n)
# 选择动作
if np.random.uniform() < epsilon:
action = np.random.choice(possible_actions) # ε-greedy策略,以一定概率随机选择动作
else:
action = possible_actions[np.argmax(policy[row_num, clo_num, possible_actions])] # 选择Q值最大的动作
# 执行动作,更新状态
next_state = get_next_state(state, action)
# 获取即时奖励
reward = grid[next_state]
# 更新策略P值
policy[state][action] = (1 - alpha) * policy[state][action] + alpha * (reward + gamma * np.max(policy[next_state]))
# 更新状态
state = next_state
route.append(state)
route_reward = sum(grid[state] for state in route)
if max_route_reward < route_reward:
max_route_reward = route_reward
best_route = route.copy()
print(f"iteration: {n_iter}, max_reward_route:{max_route_reward}, best_route:{best_route}")
route.clear()
print('-' * 100)
return best_route, max_route_reward
if __name__ == '__main__':
# 创建迷宫地图
grid = np.zeros((8, 8)) - 0.001
# 起始位置
begin_cord = (0, 0)
# 结束位置
exit_coord = (7, 7)
# 走出迷宫奖励10个积分
grid[exit_coord] = 10
# 走到墙网格,扣除20个积分
grid[0, 2] = -20
grid[0, 6] = -20
grid[1, 1] = -20
grid[1, 7] = -20
grid[2, 5] = -20
grid[3, 1] = -20
grid[3, 4] = -20
grid[3, 5] = -20
grid[3, 7] = -20
grid[4, 1] = -20
grid[4, 4] = -20
grid[5, 0] = -20
grid[5, 2] = -20
grid[5, 4] = -20
grid[5, 6] = -20
grid[5, 7] = -20
grid[6, 4] = -20
grid[7, 2] = -20
print(grid)
print('-' * 100)
max_reward_route, best_route = get_best_reward_route(grid, begin_cord, exit_coord, max_iterations=200)
print(f"max_reward_route:{max_reward_route}\nbest_route:{best_route}\n")
结果:
max_reward_route:[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3), (7, 3), (7, 4), (7, 5), (7, 6), (7, 7)]
best_route:9.986
当然结果不是唯一的,有多种路径,一样的奖励。
调试技巧:
有的时候,陷入局部最优,可增大ε-greedy策略的ε值,本文0.1->0.3
有的时候,收敛较慢,可适当调整增大墙的惩罚分数,降低空白格的奖励分数,不过一定要小于0
参考:
人工智能基础大作业-强化学习求解迷宫问题 - 知乎
第二讲 马尔可夫决策过程 - 知乎
程序员郭震:https://mp.weixin.qq.com/mp/appmsgalbum?action=getalbum&__biz=MzI3NTkyMjA4NA==&scene=24&album_id=2931825580365643777&count=3#wechat_redirect
MDPs(马尔可夫决策过程) - 简书