数据挖掘方法（1）主成分分析

声明：以下文章 来自《数据挖掘方法与模型》 (Daniel T.Larose著)[高等教育出版社]总结

一.概念

     主成分分析（principle components analysis,PCA）是指将多个变狼通过线性组合，选出较少个数的重要变量集合来描述相关结构的额一种统计分析方法，这些线性组合被称为“成分”。由m个变量组成的数据集的总变异，可以由k个线性组合变量组成的子集来标示（k

二.步骤

 

三.  关键性结论

   

     

四.应用于实际数据

    使用了1990年加利福尼亚州人口普查所有地块的普查信息。（http://lib.stat.cmu.edu/datasets/houses.zip）.

      数据描述：因变量是房屋价值的中位数；预测变量有：平均收入、居住人口数、平均房龄、家庭数、总房间数、卧室总数、所在西经及所在北纬。原始数据集有20640条记录，其中18540是从数据集中随机挑选出来的，作为训练集合，其余2100条作为测试。数据概览如下：

   

    1.使用上图的均值和标准差对变量进行标准化，得到Z向量。

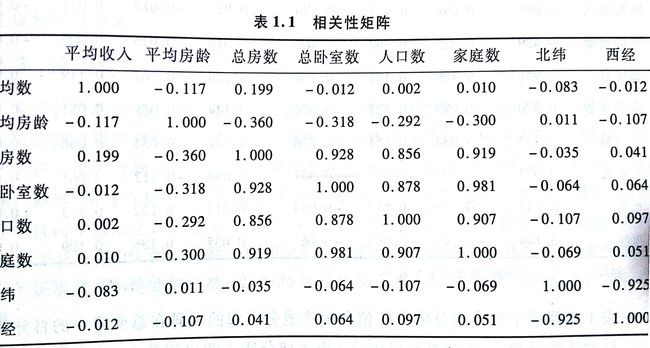
    2.研究下图中变量矩阵图以检验变量间是否存在相关性。

         

   可以看到 总房数、卧室数、人口数和家庭数之间表现出正相关性，西经和北纬表现出负相关性。再来观察变量的相关性矩阵：

    

     矩阵图和相关矩阵式常用的两种方法，用来观察预测变量之间的相关性结构。

    如果完成一次住房价预测的多元回归分析，但不考虑数据集中的多重共线性将导致回归结果非常不稳定，预测值的微小变化将会导致回归系数的极大变化，而得不到任何结论。此时需要用主成分分析，其可以通过相关化结构，确定相关变量的基本组成部分。

 3.采用主成分分析对房屋数据集进行分析，该要素矩阵（下图）中每个栏目代表成分Yi=e'Z中的一项。栏目中元素为成分的权重，代表了变量与成分的偏相关。结论2 表明这些成分的权重等于Corr(Yi,Zi),成分涉及第i个特征向量和特征值。

   

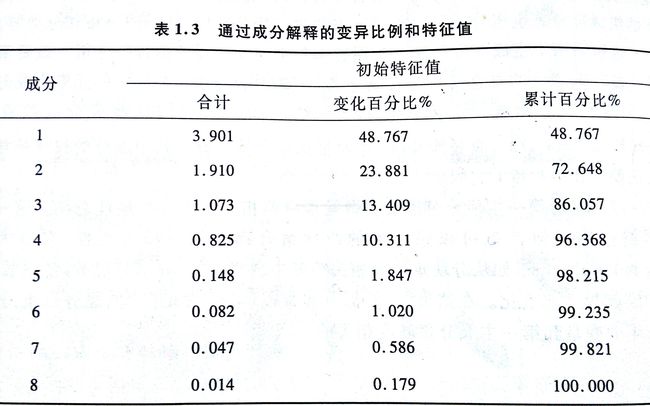
 4.结论3表明，Z的总变异种第i个主成分所占的比例是 ri/m (其中ri是特征值)，即第i个特征值与变量数的比例。由下图可以看出，第一特征值是 3.091,因为有8个预测变量，第一主成分解释 3.091/8=48.767%的变异。

   

   第二主成分Y2是次佳的变量的线性组合，前提是它与第一主成分正交。第二主成分解释了第一主成分没有解释的变异，第三主成分是第三佳变量线性组合，前提是它与前两个主成分正交。

    提取多少个主成分的指标：

   1.特征值指标：特征值总和可以解释为包含在由主成分分析得出的模型中的原始变量的个数。特征值为1意味着该成分可以解释“一个变量价值”的变异。因此，特征值大于1 的主成分应予以保留，但是小于1 的特征值也也不非一定不要。取决于变量总数

  2.解释变异的比例：若分析人员期望主成分能解释总变异的量，然后一个个选择要素，直至达到理想的解释变异比例。例如，希望主成分解释85%的变异量，可以选择第一、二、三主成分，它们解释了86.057%的变异量。

3. 碎石图。是特征值针对主成分数量的曲线，碎石图可用于查找一个上限，用来决定多少主成分应予以保留。

  碎石图的指标是：特征值-变量数量曲线开始趋于平坦的分界点便是最多主成分数量的取值。

    图中第五主成分之后曲线趋于平坦，其后所有主成分之和所解释的变异量差异不大，因此曲线几乎是水平的。该碎石图表明，应当提取的最多主成分数是4，因为第四主成分是处于曲线趋于水平之前的最近的一个成分。

   通常建议指标如下：

      .特征值指标。保留第一至第三主成分，暂不排除第四主成分。

    .解释变异的比例指标。第一至第三主成分解释了86%的变异量，增加第四主成分课提供高达96%的解释度     

    .碎石图指标。不要超过4个主成分。

   至于提取3个还是4个主成分，无绝对，需要对比如下（该表去除了主成分权重小雨0.15的值，以避免降低主成分的解释力度）：

           

   描述：

     .第一主成分，由“地块组大小”变量：总房数、总卧室数、人口数和家庭组成，这些量的大小基本同步。

     .第二主成分，是“地域”的成分，完全由西经和北纬变量构成，二者呈强负相关。

    .第三主成分，揭示了地块群体的平均收入，对于平均房龄具有相对较小的影响。也即数据集中，高平均收入与最近建成的住房相联系，而较低的平均收入与陈旧的住房相联系。

    .第四主成分，是一个没有决定是否保留的主成分，与第三主成分类似，它主要对住房平均年龄和收入有影响。

  为进一步探讨第三和第四主成分及其构成变量之间的关系，接下来要考虑因子得分。基于因子得分，我们可知：一个要素若要具有实际意义，它的权重在数值上应超过+/-0.5，各因素的权重代表其与变量之间的相关性，这样的话，因素权重的平方表示其所解释的变量的总变异，将上图中各因素权重在+/-0.5以下的去除之后，主成分描述清晰如下：

     

   注意以上4个主成分变量的分离是互斥的，这意味着任意一个变量不会被2个主成分共享，并且具有完备性，这意味着全部8个变量都包含在4个主成分内。更进一步，8个变量在4个主成分之间的分布在4-2-1-1,这与之前在表1.3中得出的它们在4个特征值之间的 3.091-1.910-1.073-0.825的分布非常接近。

4.共性。主成分分析并不提取变量的所有变异量，仅仅提取不同变量间共有的部分变异，共性所代表的正是这一部分变异。共性代表了各变量在主成分分析中的总体重要性，较高的共性值表示主成分成功地提取了初始变量中的大部分波动，较低的共性值说明数据集中仍有一些未被主成分所解释的波动。对于给定变量，共性的值等于各权重部分的平方和。现在尝试决定是否保留第四主成分，从表1,2中得到平均房龄的权重，并依此计算该变量的总体贡献值，即共性。

  总体贡献值（平均房龄，3个主成分）

      (-0.429)^2+(0.025)^2+(-0.407)^2=0.350315

  总体贡献值（平均房龄，4个主成分）

      (-0.429)^2+(0.025)^2+(-0.407)^2+(0.806)^2=0.999951

    小于0.5的总体贡献值可以认为是过低的，这意味着该变量与其他变量的共同波动不到其自身波动量的一半。现在，假设某种原因希望或需要保留平均房龄变量作为分析中的一个部分，这样只提取3个主成分将无法满足要求，因为平均房龄与其他变量只享有35%的共同波动。如果希望在分析中保留这个变量，就必须提取第四个主成分，从而将平均房龄的总体贡献值提升至50%以上。

  我们最终决定保留四个主成分，原因如下：

    .虽然特征值标准推荐3个主成分，不过并未完全否决第四个主成分。同时，对于较少的变量数（8个），该准则可能低估了应提取的主成分的最佳数目

   .解释变异的比例标准表明，如果希望对95%的变异做出解释，则应该使用4个主成分。

   .选取4个主成分并没有超过碎石图标准不超过4个主成分的要求。

   .最小共性标准表明，如果希望在分析中保留平均房龄，则必须提取第四个主成分。