代码随想录算法训练营第二十天|654. 最大二叉树|617. 合并二叉树| 98.验证二叉搜索树
654. 最大二叉树
题目:给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点,其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
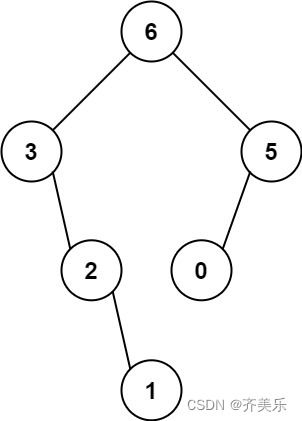
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
思路:凡是构造二叉树的题目,都要使用前序遍历,先构建出中间结点再构造它的左子树和右子树,对于本题通过题目中给出的步骤即可构建出最大二叉树。
C#代码
public class Solution {
public TreeNode ConstructMaximumBinaryTree(int[] nums) {
if(nums.Length == 0) return null;
//1.创建一个根节点,其值为 nums 中的最大值。
int rootValue = int.MinValue;
int index = 0;
for(int i = 0;i<nums.Length;i++){
if(nums[i]>rootValue){
rootValue = nums[i];
index = i;
}
}
TreeNode root = new TreeNode(rootValue);
if(nums.Length == 1) return root;
//分割左右子树
int[] leftTree = new int[index];
Array.Copy(nums,0,leftTree,0,leftTree.Length);
int[] rightTree = new int[nums.Length - index - 1];
Array.Copy(nums,index+1,rightTree,0,rightTree.Length);
//2.递归地在最大值 左边 的 子数组前缀上 构建左子树。
root.left = ConstructMaximumBinaryTree(leftTree);
//3.递归地在最大值 右边 的 子数组后缀上 构建右子树。
root.right = ConstructMaximumBinaryTree(rightTree);
return root;
}
}
代码中每次递归都要构建两个新数组,所以效率较低,可以进行优化操作。类似用数组构造二叉树的题目,每次分隔尽量不要定义新的数组,而是通过下标索引直接在原数组上操作,这样可以节约时间和空间上的开销。
优化后的方法:
public TreeNode ConstructMaximumBinaryTree1(int[] nums, int leftIndex, int rightIndex) {
if (rightIndex - leftIndex < 1) {// 没有元素了
return null;
}
if (rightIndex - leftIndex == 1) {// 只有一个元素
return new TreeNode(nums[leftIndex]);
}
int maxIndex = leftIndex;// 最大值所在位置
int maxVal = nums[maxIndex];// 最大值
for (int i = leftIndex + 1; i < rightIndex; i++) {
if (nums[i] > maxVal){
maxVal = nums[i];
maxIndex = i;
}
}
TreeNode root = new TreeNode(maxVal);
// 根据maxIndex划分左右子树
root.left = ConstructMaximumBinaryTree1(nums, leftIndex, maxIndex);
root.right = ConstructMaximumBinaryTree1(nums, maxIndex + 1, rightIndex);
return root;
}
617. 合并二叉树
题目:给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
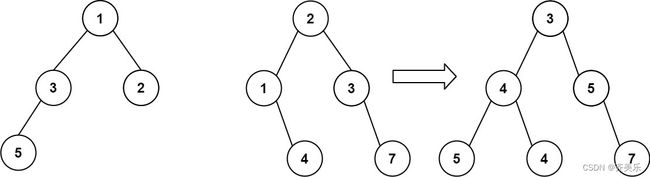
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
思路:确定终止条件,因为是传入了两个树,那么就有两个树遍历的节点t1 和 t2,如果t1 == NULL 了,两个树合并就应该是 t2 了(如果t2也为NULL也无所谓,合并之后就是NULL)。
反过来如果t2 == NULL,那么两个数合并就是t1(如果t1也为NULL也无所谓,合并之后就是NULL)。
单层递归的逻辑:可以构建一个新的树,也可以直接在t1的基础上进行构建。
C#递归代码:
public class Solution {
//前序遍历:中、左、右
public TreeNode MergeTrees(TreeNode root1, TreeNode root2) {
//终止条件
if(root1==null) return root2;
if(root2==null) return root1;
//中间结点操作
TreeNode root = new TreeNode();
root.val = root1.val + root2.val;
//左
root.left = MergeTrees(root1.left,root2.left);
//右
root.right = MergeTrees(root1.right,root2.right);
return root;
}
}
队列迭代法:
public class Solution {
public TreeNode MergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null) return root2;
if (root2 ==null) return root1;
Queue<TreeNode> queue = new Queue<TreeNode>();
queue.Enqueue(root1);
queue.Enqueue(root2);
while (queue.Any()) {
TreeNode node1 = queue.Dequeue();
TreeNode node2 = queue.Dequeue();
// 此时两个节点一定不为空,val相加
node1.val = node1.val + node2.val;
// 如果两棵树左节点都不为空,加入队列
if (node1.left != null && node2.left != null) {
queue.Enqueue(node1.left);
queue.Enqueue(node2.left);
}
// 如果两棵树右节点都不为空,加入队列
if (node1.right != null && node2.right != null) {
queue.Enqueue(node1.right);
queue.Enqueue(node2.right);
}
// 若node1的左节点为空,直接赋值
if (node1.left == null && node2.left != null) {
node1.left = node2.left;
}
// 若node1的右节点为空,直接赋值
if (node1.right == null && node2.right != null) {
node1.right = node2.right;
}
}
return root1;
}
}
700. 二叉搜索树中的搜索
题目:给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
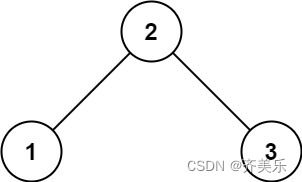
输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
知识点:二叉搜索树(BST,Binary Search Tree),也称二叉排序树或二叉查找树。
二叉搜索树:一棵二叉树,可以为空;如果不为空,满足以下性质:
- 非空左子树的所有键值小于其根结点的键值。
- 非空右子树的所有键值大于其根结点的键值。
- 左、右子树都是二叉搜索树。
思路:通过二叉搜索树的性质,可以明确搜索方向,不需要将所有结点都遍历一遍。
C#递归代码:
public class Solution {
public TreeNode SearchBST(TreeNode root, int val) {
if(root == null || root.val == val) return root;
TreeNode result = null;
if(val < root.val) result = SearchBST(root.left,val);
if(val > root.val) result = SearchBST(root.right,val);
return result;
}
}
C#迭代代码:
public class Solution {
public TreeNode SearchBST(TreeNode root, int val) {
while(root != null){
if(root.val == val) return root;
if(val < root.val) root = root.left;
else root = root.right;
}
return null;
}
}
98. 验证二叉搜索树
题目:给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
输入:root = [2,1,3]
输出:true
思路一:通过二叉搜索树的性质可知,它的中序序列数组是递增序列,只要验证他的中序序列数组即可。(暴力解法,效率较低)
思路二:定义一个初始是最小值的maxValue变量,代表当前遇到的元素的最大值,然后中序递归遍历,将每个结点都和他比较,因为二叉搜索树的中序遍历是递增的,如果当前大于它(记录的是前一个元素的值),就把当前结点的值赋值给这个变量,如果小于他则说明这不符合二叉搜索树。(存在一个极端情况的bug,如果树中最小值和初始化maxValue变量的最小值相等,则会导致结果错误)
思路三:双指针法,定义一个一直指向前一个元素的指针,如果前一个元素大于了当前元素,则说明不符合二叉搜索树的特性。(推荐使用)
C#中序递归,思路三:
public class Solution {
TreeNode previous = null;
public bool IsValidBST(TreeNode root) {
if(root == null) return true;
//左
bool leftTree = IsValidBST(root.left);
//中
if(previous != null && previous.val>=root.val) return false;
previous = root;
//右
bool rightTree = IsValidBST(root.right);
return leftTree&&rightTree;
}
}