数据结构与算法基础-学习-32-选择排序之简单选择排序、堆排序
目录
一、简单选择排序基本思路
二、简单选择排序基本操作
三、简单选择排序算法思路
四、简单选择排序代码
1、SimpleSelectSortSentrySqQueue
五、简单选择排序算法分析
1、记录移动次数
2、记录比较次数
六、简单选择排序Linux环境编译测试
七、堆的定义
八、堆调整
1、小根堆
2、大根堆
九、堆排序的算法思路
1、调整为大根堆
2、堆调整为升序序列
十、堆排序代码
1、HeapSiftSentrySqQueue
2、HeapSortSentrySqQueue
十一、堆排序算法分析
1、最大优点
2、辅助存储空间
3、适用情况
十二、堆排序Linux环境编译测试
排序的其他相关知识点和源码分享可以参考之前的博客:
《数据结构与算法基础-学习-30-插入排序之直接插入排序、二分插入排序、希尔排序》,
《数据结构与算法基础-学习-31-交换排序之冒泡排序、快速排序》
一、简单选择排序基本思路
在待排序的数据中选出最大(小)的元素放在其最终的位置。
二、简单选择排序基本操作
1、首先通过n-1次关键字比较,从n个记录中找出关键字最小的记录,将它与第一个记录交换。
2、再通过n-2次比较,从剩余的n-1个记录中找出关键字次小的记录,将它与第二个记录交换。
3、重复上述操作,共进行n-1趟排序后,排序结束。
三、简单选择排序算法思路
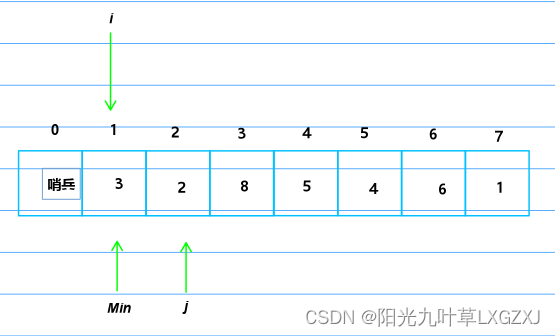
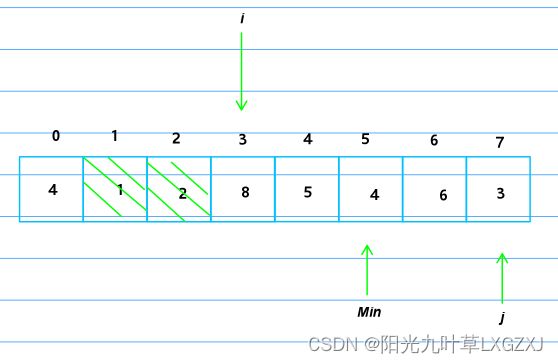
我们还是以这个图为例来进行介绍,升序排列。Min指向最小值的索引号,i表示最小值需要插入的位置,j表示需要比较的元素。
先将1号位的3移动到哨兵位,存储最小值的实际值,Min初始化为1号位,j从Min加一的位置开始扫描。
发现j的2比哨兵的3小,将哨兵位放上2,Min记录最小索引2,j继续向后扫描。
发现j的8比哨兵的2大,j继续向后扫描。
发现j的5比哨兵的2大,j继续向后扫描。
发现j的4比哨兵的2大,j继续向后扫描。
发现j的6比哨兵的2大,j继续向后扫描。
发现j的1比哨兵的2小,将哨兵位放上1,Min记录最小索引7,所有元素已经扫描一遍,已经找到最小值。
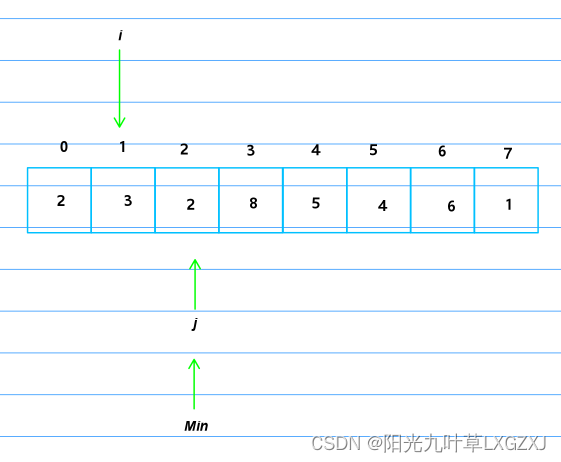
将Min和i索引所存储的元素交换,这就得到最小值1了,1号位不需要再扫描了,i继续右移,Min还是以需要扫描的第一个元素为最小值设为2,j初始化为i加1等于3。
快进一下,不然画的图太多了,8,5,4,6,3都比2大,所以只需要右移j。
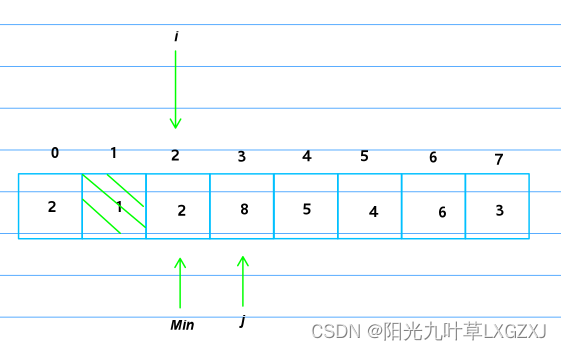
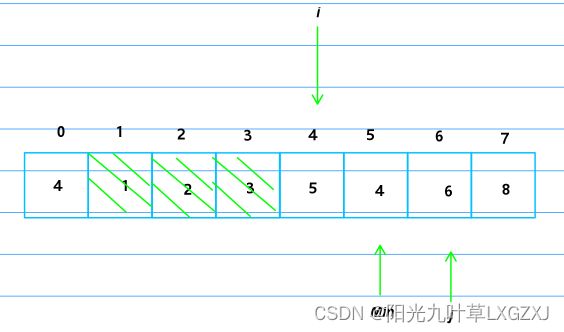
2号位不需要再扫描了,i继续右移,Min还是以需要扫描的第一个元素为最小值设为3,j初始化为i加1等于4,j开始右移。
发现j的5比哨兵的8小,将哨兵位放上5,Min记录最小索引4,j继续向后扫描。
发现j的4比哨兵的5小,将哨兵位放上4,Min记录最小索引5,j继续向后扫描。
发现j的6比哨兵的4大,j继续向后扫描。
发现j的3比哨兵的4小,将哨兵位放上3,Min记录最小索引7,所有元素已经扫描一遍,已经找到最小值。
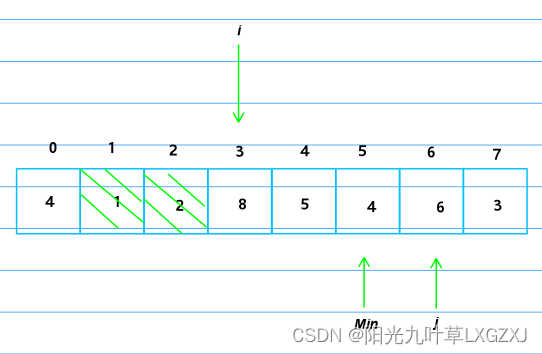
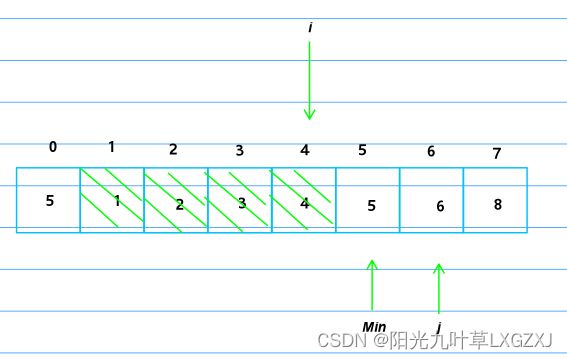
3号位不需要再扫描了,i继续右移,Min还是以需要扫描的第一个元素为最小值设为4,j初始化为i加1等于5,j开始右移。
发现j的4比哨兵的5小,将哨兵位放上4,Min记录最小索引5,j继续向后扫描。
发现6,8比哨兵的4大,所有元素已经扫描一遍,已经找到最小值。
虽然数据到这里已经有序了,但其实后面还需要按照前面的逻辑再把数据扫描一遍。
四、简单选择排序代码
1、SimpleSelectSortSentrySqQueue
Status SimpleSelectSortSentrySqQueue(SqQueue* Queue)
{
JudgeAllNullPointer(Queue);
if (Queue->Flag != INT_TYPE_FLAG)
{
return FailFlag;
}
QueueLenType i;
QueueLenType j;
int* Array = (int*)(Queue->Data);
QueueLenType MinIndex;
for (i = 1; i < Queue->SqQueueLen - 1; i++)//n个元素需要n-1趟,才能全部排列好。
{
MinIndex = i;
Array[0] = Array[i];
for (j = i + 1; j < Queue->SqQueueLen; j++)//排好序的元素不需要再进行比较。
{
if (Array[j] < Array[0])//寻找最小值
{
Array[0] = Array[j];
MinIndex = j;
}
}
if (i != MinIndex)//判断是否交换
{
Array[MinIndex] = Array[i];
Array[i] = Array[0];
}
}
LogFormat(Debug,"Simple Select Sort SqQueue OK.\n");
return SuccessFlag;
}
五、简单选择排序算法分析
| 情况 | 时间复杂度 | 是否稳定 |
| 最好 | O(n^2) | 不稳定 |
| 最坏 | O(n^2) | |
| 平均 | O(n^2) |
1、记录移动次数
最坏是怎么算出来的呢,n个元素最多只用移动n-1次,数据存放到哨兵一次,最小值的位置和最小值需要移动到的正确位置进行交换需要两次,一共三次,所以是3(n - 1)。
| 情况 | 次数 |
| 最好 | 0 |
| 最坏 | 3(n - 1) |
2、记录比较次数
无论待排序列处于上面状态,选择排序所需进行的比较次数都相同。
n个元素需要比较n-1次可以找出最大或最小值。
找到的元素不用再比较,n-1个元素需要比较n-2次可以找出最大或最小值。
也就是一共需要比较
n-1 + n-2 + n-3 + ... + 1 = (n-1 + 1) * (n-1) / 2 = (n - 1) * n / 2。
六、简单选择排序Linux环境编译测试
[gbase@czg2 Sort]$ make
gcc -Wall -Wextra -O3 InsertSort.c SwapSort.c SelectSort.c MergeSort.c BucketSort.c main.c -o TestSort -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/Log/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/HashTable/include/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/SqQueue/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/SqStack/ -L /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/Make/Libs/ -lPublicFunction -lLog -lSqQueue
[gbase@czg2 Sort]$ ./TestSort
2023-9-8--[ Info ]--SqQueue Data :
Data : [ 0 ,50 ,51 ,52 ,53 ,54 ,55 ,56 ,57 ,58 ,59 ,60 ,61 ,62 ,63 ,64 ,65 ,66 ,67 ,68 ,69 ,70 ,71 ,72 ,73 ,74 ,75 ,76 ,77 ,78 ,79 ,80 ,81 ,82 ,83 ,84 ,85 ,86 ,87 ,88 ,89 ,90 ,91 ,92 ,93 ,94 ,95 ,96 ,97 ,98 ,99 ,0 ,1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ,44 ,45 ,46 ,47 ,48 ,49 ]
FrontIndex : 0
RearIndex : 0
SqQueueLen : 101
SqQueueMaxLen : 101
Flag : INT_TYPE_FLAG
2023-9-8--[ Info ]--Sort Function Elapsed Time : 0 s
2023-9-8--[ Info ]--SqQueue Data :
Data : [ 98 ,0 ,1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ,16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ,34 ,35 ,36 ,37 ,38 ,39 ,40 ,41 ,42 ,43 ,44 ,45 ,46 ,47 ,48 ,49 ,50 ,51 ,52 ,53 ,54 ,55 ,56 ,57 ,58 ,59 ,60 ,61 ,62 ,63 ,64 ,65 ,66 ,67 ,68 ,69 ,70 ,71 ,72 ,73 ,74 ,75 ,76 ,77 ,78 ,79 ,80 ,81 ,82 ,83 ,84 ,85 ,86 ,87 ,88 ,89 ,90 ,91 ,92 ,93 ,94 ,95 ,96 ,97 ,98 ,99 ]
FrontIndex : 0
RearIndex : 0
SqQueueLen : 101
SqQueueMaxLen : 101
Flag : INT_TYPE_FLAG七、堆的定义
若有n个元素的序列{a1,a2,...,an}满足(ai <= a2i 和 ai <= a2i+1)或(ai >= a2i 和 ai >= a2i+1),则分别称为该序列为小根堆和大根堆。
堆的实质是满足如下性质的完全二叉树:二叉树中任一非叶子节点均小于或大于它的孩子结点。
八、堆调整
如何再输出堆顶元素后,调整剩余元素为一个新的堆?
升序为例。
1、小根堆
(1)输出堆顶元素之后,以堆中最后一个元素代替之。
(2)将根节点值与左右子树的根节点值进行比较,并于其中小者进行交换。
(3)重复上述操作,直至叶子节点,将得到新的堆,称这个从堆顶至叶子的调整过程为筛选。
2、大根堆
(1)以堆中最后一个元素代替之根节点的元素,输出堆顶元素。
(2)将根节点值与左右子树的根节点值进行比较,并于其中小者进行交换。
(3)重复上述操作,直至叶子节点,将得到新的堆,称这个从堆顶至叶子的调整过程为筛选。
九、堆排序的算法思路
推排序的实现需要两个大的步骤,一是将待排序的元素调整为大根堆或小根堆。二、堆调整为升序或降序序列。
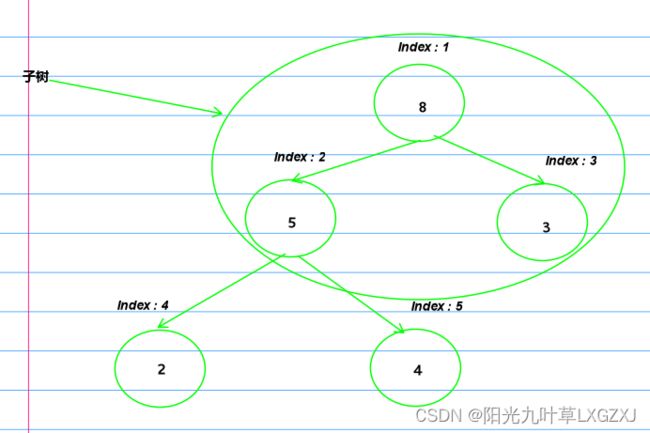
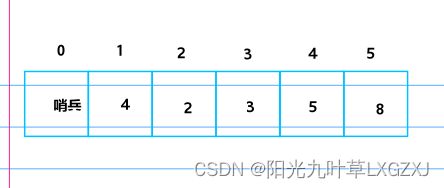
我们这里以大根堆、升序排列为例,待排元素如下:
1、调整为大根堆
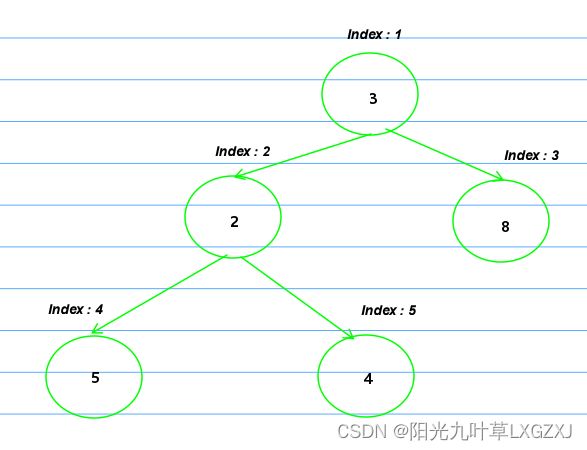
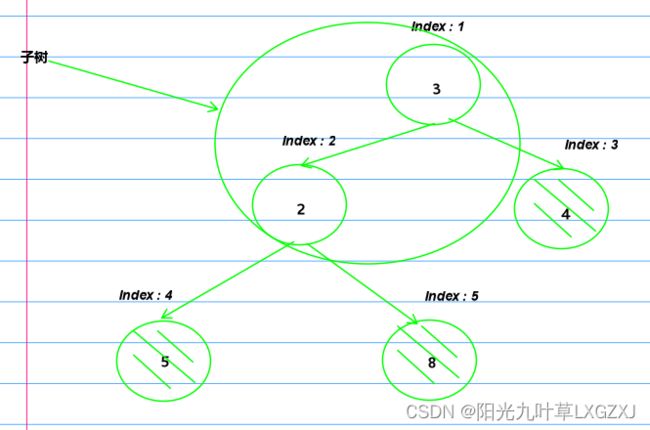
(1)我们需要想把上面的数组想象成满二叉树,如下:
(2)我们的思路是从下到上进行堆调整,需要先把这个树的子树调整为大根堆,上面的双亲结点才能调整成大根堆。
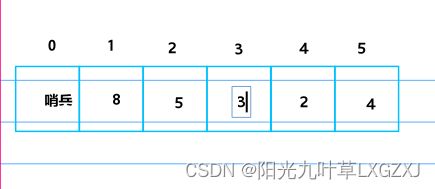
(3)5和4中的最大者5和2进行交换,那这个子树已经调整为大根堆。
(4)数组也变化了。
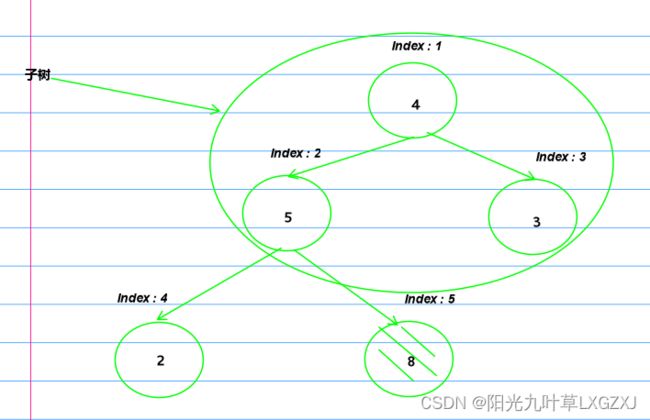
(5)接下来我们来调整这棵树。
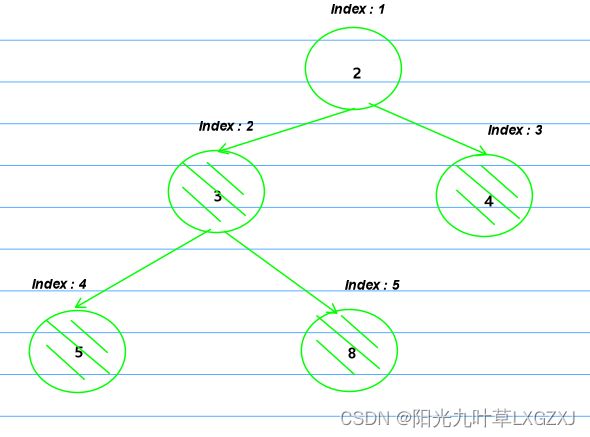
(6)5和8中的最大者8和3进行交换,那这个子树已经调整为大根堆。
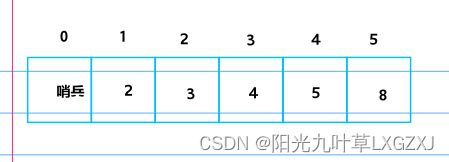
(7)那这整棵树就已经变成大根堆了,对应的数组也变化了。
2、堆调整为升序序列
现在我们从上到下进行排序。
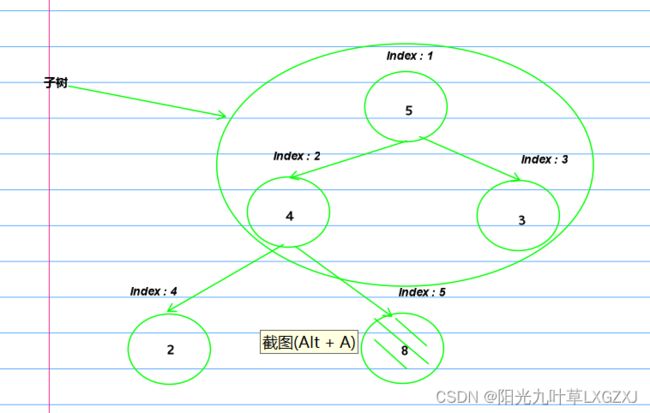
(1)第一个结点和最后一个交换位置,是不是感觉出什么了,最后一个元素变为最大值了,变换位置之后这棵子树就不是大根堆了,我们来开始调整。
(2)5和3中的最大者5和4进行交换,那这个子树已经调整为大根堆。
(3)刚刚Index:2变化了,我们看一下这颗子树是否需要调整,发现就是大根堆,可以不调整,欧耶,Index:5不需要调整记得哈。
(4)实际数组变化如下
(5)第一个结点和最后一个Index:4交换位置,变换位置之后这棵子树就不是大根堆了,我们来开始调整。
(6)4和3中的最大者4和2进行交换,那这个子树已经调整为大根堆。
(7)实际数组变化如下
(8)第一个结点和最后一个Index:3交换位置,变换位置之后这棵子树就不是大根堆了,我们来开始调整。
(9)发现不需要调整,本来就是大根堆,完美。
(10)那我们交换一下第一个结点和最后一个Index:2交换位置。n个元素需要调整n-1次,五个元素我们已经调整了4次,堆已经是升序排列了。
(11)实际数组变化如下
十、堆排序代码
1、HeapSiftSentrySqQueue
Status HeapSiftSentrySqQueue(SqQueue* Queue, QueueLenType StartSiftIndex, QueueLenType EndSiftIndex)
{
JudgeAllNullPointer(Queue);
QueueLenType i = StartSiftIndex;
QueueLenType j = 2 * i;
int* Array = (int*)(Queue->Data);
while (j <= EndSiftIndex)//满足的话,表示有左右子树。
{
if (j < EndSiftIndex && Array[j] < Array[j + 1])//第一个条件成立的话,表示还有右子树。如果右子树大于左子树,将索引号移动到右子树上。
{
j++;
}
if (Array[i] < Array[j])//子树与根节点比较,如果子树大,进入此判断,进行数据交换。
{
Array[0] = Array[i];
Array[i] = Array[j];
Array[j] = Array[0];
}
i = j; //移动到下一个子树的根节点。
j = 2 * i;//移动到下一个子树的根节点的子树。
}
LogFormat(Debug,"Heap Sift Sentry SqQueue OK.\n");
return SuccessFlag;
}2、HeapSortSentrySqQueue
//需要一个哨兵,也就是预留位置,为的是方便通过数组计算左右子树。
Status HeapSortSentrySqQueue(SqQueue* Queue)
{
JudgeAllNullPointer(Queue);
if (Queue->Flag != INT_TYPE_FLAG)
{
return FailFlag;
}
QueueLenType i;
QueueLenType EndIndex = Queue->SqQueueLen - 1;
int* Array = (int*)(Queue->Data);
for (i = EndIndex / 2; i >= 1; i--)//从下往上建立大根堆
{
HeapSiftSentrySqQueue(Queue, i, EndIndex);
}
//堆调整变化为升序序列,从上往下进行调整。
//n个元素需要调整n-1次。
for (i = 1; i <= EndIndex - 1; i++)
{
Array[0] = Array[1];
Array[1] = Array[EndIndex - i + 1];
Array[EndIndex - i + 1] = Array[0];
HeapSiftSentrySqQueue(Queue, 1, EndIndex - i);
}
LogFormat(Debug,"Heap Sort Sentry SqQueue OK.\n");
return SuccessFlag;
}十一、堆排序算法分析
| 情况 | 时间复杂度 | 是否稳定 |
| 最好 | O(n * log2^n) | 不稳定 |
| 最坏 | O(n * log2^n) | |
| 平均 | O(n * log2^n) |
1、最大优点
堆排序在最坏情况、最好情况下都是O(n * log2^n),都不会使排序处于
最优或最差的状态。
2、辅助存储空间
仅需要一个辅助空间,也就是哨兵位或0号位。
3、适用情况
适用于待排序记录个数n较大的情况。
十二、堆排序Linux环境编译测试
[gbase@czg2 Sort]$ make
gcc -Wall -Wextra -O3 InsertSort.c SwapSort.c SelectSort.c MergeSort.c BucketSort.c main.c -o TestSort -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/Log/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/HashTable/include/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/SqQueue/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/SqStack/ -L /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/Make/Libs/ -lPublicFunction -lLog -lSqQueue
[gbase@czg2 Sort]$ time ./TestSort
2023-9-8--[ Debug ]--Init SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Debug ]--Enter SqQueue OK
2023-9-8--[ Info ]--SqQueue Data :
Data : [ 0 ,5 ,6 ,7 ,8 ,9 ,0 ,1 ,2 ,3 ,4 ]
FrontIndex : 0
RearIndex : 0
SqQueueLen : 11
SqQueueMaxLen : 11
Flag : INT_TYPE_FLAG
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sift Sentry SqQueue OK.
2023-9-8--[ Debug ]--Heap Sort Sentry SqQueue OK.
2023-9-8--[ Info ]--Sort Function Elapsed Time : 0 s
2023-9-8--[ Info ]--SqQueue Data :
Data : [ 1 ,0 ,1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 ]
FrontIndex : 0
RearIndex : 0
SqQueueLen : 11
SqQueueMaxLen : 11
Flag : INT_TYPE_FLAG
2023-9-8--[ Debug ]--Destroy SqQueue OK
real 0m0.003s
user 0m0.001s
sys 0m0.001s