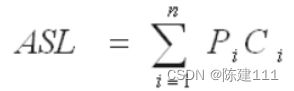软件设计师-8.算法分析与设计

8.1 算法设计与分析的基本概念

1）算法

算法是对特定问题求解步骤的一种描述，它是指令的有限序列，其中每条指令表示一个或多个操作。

算法特性：

• 有穷性
• 确定性
• 可行性
• 输入
• 输出

2）算法设计

一个好的算法应考虑多个目标，包括正确性、可读性、健壮性和高效性等。

算法设计技术主要有分治法、动态规划法、贪心法、回溯法、分支限界法，概率算法和近似算法等。

3）算法分析

算法分析技术的主要内容：

• 选择算法标准：正确性、可靠性、简单性、易理解性
• 算法的时间复杂度和空间复杂度要低

4）算法表示

算法表示方法：

1. 自然语言：优点是容易理解。缺点是容易出现二义性，且算法冗长。
2. 流程图：优点是直观易懂。缺点是严密性不如程序设计语言、灵活性不如自然语言。
3. 程序设计语言：优点是计算机能执行。缺点是抽象性差，拘泥于细节
4. 伪代码：介于自然语言和程序设计语言之间的方法，它采用某种程序设计语言的基本语法，同时结合自然语言来表达。

8.2 算法分析基础

1）时间复杂度

由于时间复杂度与空间复杂度分别对算法占用的时间和空间资源进行分析，计算方法相似，且空间复杂度分析相对简单，因此主要讨论时间复杂度。算法时间复杂度分析主要是分析算法的运行时间。

建立以输入规模n为自变量的函数 T(n)来表示时间复杂度。根据不同的输入，将算法复杂度分析分为3种情况：

1. 最佳情况：执行时间最少的输入

2. 最坏情况：执行时间最多的输入

3. 平均情况：算法的平均运行时间。考虑的是每种输入极其输入的概率。平均情况分析按以下3个步骤进行：

   1. 将所有的输入按其执行时间分类
   2. 确定没类输入发生的概率
   3. 确定没类输入执行的时间

   下列给出平均情况下的复杂度分析：

    

   pi 第i类输入发生的概率，ci 第i类输入的执行时间，输入分为 n 类。

2）渐进符号

以输入规模n为自变量建立的时间复杂度实际上还是较复杂的，可以对该函数做进一步的抽象，仅考虑运行时间的增长率或称为增长的重量。当输入规模大到只有与运行时间的增长量级有关时，就是在研究算法的渐进效率。下面介绍3种常用的标准方法来简化算法的渐进分析：

1. O记号。定义为：给定一个函数 g(n)，O(g(n)) = { f(n): 存在正常数 c 和 n₀，当n≥n₀，有 f(n)≤cg(n) }，如图所示。O(g(n))表示一个函数集合，往往用该记号求出算法的渐进上界。

    

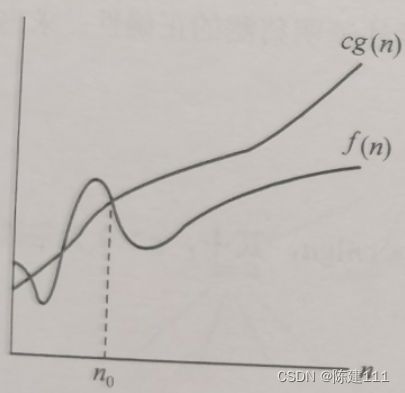
2. Ω记号。定义为：给定一个函数 g(n)，Ω(g(n)) = { f(n): 存在正常数 c 和 n₀，当n≥n₀，有 f(n)≥cg(n) }，如图所示。Ω(g(n))表示一个函数集合，往往用该记号求出算法的渐进下界。

    

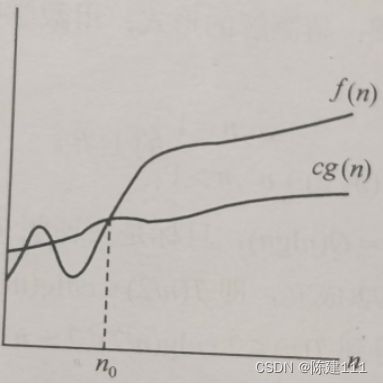
3. ⊙记号。定义为：给定一个函数 g(n)，⊙(g(n)) = { f(n): 存在正常数 c₁、c₂ 和 n₀，当n≥n₀，有 c₁g(n)≤f(n)≤c₂g(n) }，如图所示。⊙(g(n))表示一个函数集合，往往用该记号求出算法的渐进上界和渐进下界，即渐进紧致界。

    

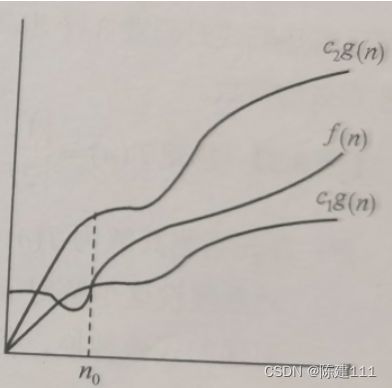
由上述定义可知， f(n)=⊙(g(n)) 当且仅当 f(n)=O(g(n)) 和 f(n)=Ω(g(n))

3）递归式

递归算法的时间复杂度：

1. 展开法：将递归式中等式右边的项根据递归式进行替换，称为展开。展开后的项再被展开，如此下去，直到得到一个求和表达式，得到结果。

   当n=1时T(n)=1，当n>1时T(n)= T(n-1)+n，求时间复杂度

   T(n)= T(n-1)+n

   T(n-1)= T(n-2)+n-1

   ...

   T(2) = T(1) + 2

   根据展开法原则， T(n) = 1+2+...+n = n(n+1)/2=O(n²)

2. 代换法：先猜测一个较小值，再用数学归纳法证明猜测的正确性，这种方法比较难用。

3. 递归树法

4. 主方法：也称主定理，给出了求解以下形式的递归式的快速方法

   T(n)=aT(n/e)+f(n)

   其中 a≥1 e≥1 ,f(n)是一个渐进的正函数。T(n) 可能有如下渐进紧致界：

   • 若对常数 ε > 0，有 f(n) = O( n^(logₑa-ε) )，则T(n) = ⊙(n²)
   • 若 f(n) = ⊙( n^(logₑa) lgᵏ n )，则 T(n) = ⊙( n^(logₑa) lgᵏ⁺¹ n )
   • 若 ε > 0，有 f(n) = O( n^(logₑa+ε) ) ，且对于常数 c<1与足够大的 n 有 af(b/n) ≤ cf(n)，则T(n) = ⊙(f(n))

8.3 分治法

1）递归的概念

递归 = 递推 + 回溯。

递归是指子程序（或函数）直接或间接调用自己，是一种描述问题和解决问题的常用方法。

递归有两个基本要是：

• 边界条件：确定递归到何时终止，也称递归出口。
• 递归模式：大问题如何分解为小问题，也称递归体。

例如阶乘函数：当n=0时n!=1，当n>0时 n!=n(n-1)!。n=0为边界条件， n(n-1)! 是递归体。n!可以递归地计算如下：

int factorial(int num) {
    if(num == 0) {
        return 1;
    }
    if(num > 0) {
        return num * factorial(num-1);
    }
}

2）分治法的基本思想

分治和递归就像孪生兄弟。分治法的思想是将一个难以直接解决的大问题分解成一些规模较小的相同问题，这些问题互相独立，分而治之。

一般来说，分治法在每一层递归上都有3个步骤：

1. 分解。将原问题分解成一些列子问题。
2. 求解。递归地求解各个子问题。若子问题足够小，则直接求解。
3. 合并。将子问题的解合并成原问题的解。

3）分支算法经典实例

归并排序算法

归并排序算法是成功应用分治法的一个完美例子，其基本思想是将待排序元素分成大小相同的两个子序列，分别对子序列进行排序，最终将拍好序的子序列合并为所要求的的序列。归并算法按照分治法的3个步骤：

1. 分解。将n个元素分成各 n/2 个元素的子序列。
2. 求解。用归并排序对各个子序列递归的排序。
3. 合并。合并两个已经排好序的子序列以得到排序结果。

    void mergeSort(int[] arr,int left,int right,int[] temp) {
        if (left

例如我们使用例子调用函数

    public static void main(String[] args) {
        int []arr = {1,3,6,2,3,7,8,10};
        int[] tmp = new int[arr.length];
        MyTest myTest = new MyTest();
        System.out.println(Arrays.toString(arr));
        myTest.mergeSort(arr, 0, arr.length-1, tmp);
        System.out.println(Arrays.toString(arr));
    }

数组{1,3,6,2,3,7,8,10} 长度为8，初始传入参数为mergeSort(arr, 0, 7, tmp)，调用的逻辑如下：

1. 进入函数mergeSort(arr, 0, 7, tmp)，未到达终止条件。计算 mid = 3，需向左分解（递推） 即 mergeSort(arr, 0, 3, tmp)
2. 进入函数mergeSort(arr, 0, 3, tmp)，未到达终止条件。计算 mid = 1，需向左分解（递推） 即 mergeSort(arr, 0, 1, tmp)
3. 进入函数mergeSort(arr, 0, 1, tmp)，未到达终止条件。计算 mid = 0，需向左分解（递推） 即 mergeSort(arr, 0, 0, tmp)
4. 进入函数mergeSort(arr, 0, 0, tmp)，到达终止条件，需返回（回溯）到mergeSort(arr, 0, 1, tmp)中；
5. 返回到mergeSort(arr, 0, 1, tmp)，继续执行向右分解（递推）即mergeSort(arr, 1, 1, tmp)
6. 进入函数mergeSort(arr, 1, 1, tmp)，到达终止条件，需返回（回溯）到mergeSort(arr, 0, 1, tmp)中；
7. 返回到mergeSort(arr, 0, 1, tmp)，继续执行 merge()，合并 数组0，1下标元素。合并完成后需返回（回溯）到mergeSort(arr, 0, 3, tmp)
8. 返回到mergeSort(arr, 0, 3, tmp)，继续执行向右分解（递推）即mergeSort(arr, 2, 3, tmp)
9. 进入函数mergeSort(arr, 2, 3, tmp)，未到达终止条件。计算 mid = 2，需向左分解（递推） 即 mergeSort(arr, 2, 2, tmp)
10. 进入函数mergeSort(arr, 2, 2, tmp)，到达终止条件，需返回（回溯）到mergeSort(arr, 2, 3, tmp)中；
11. 返回到mergeSort(arr, 2, 3, tmp)，继续执行向右分解（递推）即mergeSort(arr, 3, 3, tmp)
12. 进入函数mergeSort(arr, 3, 3, tmp)，到达终止条件，需返回（回溯）到mergeSort(arr, 2, 3, tmp)中；
13. 返回到mergeSort(arr, 2, 3, tmp)，继续执行 merge()，合并 数组2，3下标元素。合并完成后需返回（回溯）到mergeSort(arr, 0, 3, tmp)
14. 返回到mergeSort(arr, 0, 3, tmp)，继续执行 merge()，合并 数组1，2，3，4下标元素。合并完成后需返回（回溯）到mergeSort(arr, 0, 7, tmp)，至此 0,7以完成前半部分的排序。
15. 进入函数mergeSort(arr, 0, 7, tmp)，继续执行向右分解（递推）即mergeSort(arr, 4, 7, tmp)。
16. ...(递归过程与 0~3 一致)
17. 最终返回（回溯）到mergeSort(arr, 0, 7, tmp)，继续执行 merge()，合并 数组1，2，3，4，5, 6, 7下标元素。完成整个排序

最大子段和问题

给定长度为n的整数序列，a[1...n], 求[1,n]某个子区间[i , j]使得a[i]+…+a[j]和最大。例如(-2,11,-4,13,-5,2)的最大子段和为20,所求子区间为[2,4]。

分治策略如下：

1. 分解：将所给的序列a[1...n]分为长度相等的两段 a[1...n/2] 和 a[n/2+1 ... n]，分别求出这两段的最大字段和，则a[1...n]的最大字段和有3中情况
   • a[1...n]的最大字段和与a[1...n/2]相等
   • a[1...n]的最大字段和与a[n/2+1 ... n]相等
   • 最大字段和的区间为 [i , j]，且 1≤ i≤ n/2， n/2+1≤ j≤ n
2. 求解：1和2这两种情况可递归求得。对于情形3，容易看出 a[n/2] 和 a[n/2+1]在最优子列中。因此可以在a[1...n/2]中计算出 最大子段和s1，并在a[n/2+1 ... n]中计算出 最大子段和s2。则s1+s2为情形3的最优值。
3. 合并：比较在分解阶段的3情况下的最大字段和，取3者中较大者为原问题的解。

    int maxsum(int arr[], int left, int right)//返回左闭右开区间的最大连续和
    {
        int sum = 0;
        int i;
        if (left == right) { //分解到单个整数，不可继续分解
            if (arr[left] > 0) { return arr[left]; }
            else { return 0; }
        }
        // 从 left 和 right 的中间分解数组
        int mid = (left + right) / 2;
        int leftsum = maxsum(arr, left,mid);
        int rightsum = maxsum(arr, mid+1, right);
        //判断是情形1、情形2还是情形3
        int s1=0; // 左侧最优值
        int lefts = 0;
        for(i = mid; i >= left; i--){
            lefts += arr[i];
            if (lefts > s1) { s1 = lefts; }
        }
        int s2=0; // 右侧最优值
        int rights = 0;
        for(i = mid+1; i <= right; i++){
            rights += arr[i];
            if (rights > s2) { s2 = rights; }
        }
        sum = s1+s2;
        //情形1
        if (sum < leftsum) { sum = leftsum; }
        //情形2
        if (sum < rightsum) { sum = rightsum; }
        //如果不是情形1、情形2，则是情形3
        return sum;
    }

8.4 动态规划法

8.4.1 动态规划法的基本思想

动态规划法与分治法类似，其基本思想也是将待求解问题分成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。但不同的是，分治法在子问题和子子问题等上被重复计算了很多次，而动态规划则具有记忆性，通过填写表把所有已经解决的子问题答案纪录下来，在新问题里需要用到的子问题可以直接提取，避免了重复计算，从而节约了时间，所以在问题满足最优性原理之后，用动态规划解决问题的核心就在于填表，表填写完毕，最优解也就找到。

最优性原理是动态规划的基础，最优性原理是指“多阶段决策过程的最优决策序列具有这样的性质：不论初始状态和初始决策如何，对于前面决策所造成的某一状态而言，其后各阶段的决策序列必须构成最优策略”。

设计一个动态规划法步骤：

1. 找出最优解的性质，并刻画其最结构特征。
2. 递归地定义最优解的值。
3. 以自底向上的方式计算出最优值。
4. 根据计算最优值时得到的信息，构造一个最优解。

对于一个给定问题，若具有以下性质，可以考虑使用动态规划法来求解：

1. 最优子结构。如果一个问题的最优解中包含了其子问题的最优解，就说该问题具有最优子结构。
2. 重叠子问题。当一个递归算法不断地调用同一个问题时，说明该问题包含重叠子问题。分治法每次遇到的子问题都会视为新问题，降低算法的效率，而动态规划法总是充分利用重叠子问题，对每个子问题仅计算一次，并保存到表中，而每次查表的时间为常数。

8.4.2 动态规划法的典型实例

背包问题

给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 wi，其价值为 vi。问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

问题分析

面对每个物品，我们只有选择拿(1)取或者不拿(0)两种选择，不能选择装入某物品的一部分，也不能装入同一物品多次。 把物品随机排成一排，标记为1、 2、 3……，从1号物品开始依次判断是否装包，面对当前物品有两种情况：

1. 该物品的重量大于背包的容量，装不下，只能选择不装

2. 该物品的重量小于背包的容量，可以装下，但是否要装，需要进一步判断，因为可能存在这样一种情况：要装该物品，就必须拿出之前装的一个物品，而这时可能会出现如下不同情况：

   • 【拿掉之前的一个物品并装进当前物品后 背包的总价值】<【不拿掉之前的物品且不装当前物品 背包的总价值】
   • 【拿掉之前的一个物品并装进当前物品后 背包的总价值】>【不拿掉之前的物品且不装当前物品 背包的总价值】

   举例说明：有2个物品，重量数组w={7,6}，价值数组v={3,9}，背包容量为8。1号物品重量7小于背包容量8，放进背包，此时背包价值为3，到2号物品时，2号物品重量3也小于背包容量8，但是如果要把2号物品放进背包，就要把1号物品从背包中拿出，此时就要比较两种情况下背包的价值哪个更大，max（2号物品不放进背包，2号物品放进背包（隐含着要把1号物品取出背包））=max（3,9）=9，因此选择拿出1号物品，放进2号物品。

   当然背包容量也有可能不用取出之前的物品可以直接放下当前物品，此时肯定是放要比不放价值更大。 因此，当物品重量小于背包总容量，也就是背包可以装下该物品时，要判断装之前和装之后背包的总价值来决定是否要装该物品。

因此，通过判断当前物品是否装包而计算当前问题的最优解时，是要用到上一个子问题的最优解的（通过判断上一个物品是否装包而计算得到），也就是说，如果当前物品不装进背包，那么上一个子问题的最优解就是当前状态的最优解，如果当前物品装包后的价值大于不装的价值，那么当前问题的最优解就是当前物品装进背包后产生的价值，这个值=上一个子问题中背包容量为【背包总容量减去当前物品重量】的情况下的最优解+当前物品价值。总之，当前问题的最优解求解过程依托于上一个子问题的各个状态下的最优解，所以在求当前问题的最优解之前要先求出之前的所有情况下的最优解。也就是要先求子问题的最优解。这里就需要用到动态规划的方法。

动态规划

动态规划（Dynamic Programming,DP) 与分治法的区别在于划分的子问题是有重叠的，解过程中对于重叠的部分只要求解一次，记录下结果，减少了重复计算过程。

另外，DP在求解一个问题最优解时，不是固定的计算合并某些子问题的解，而是根据各子问题的解的情况选择其中最优的。

动态规划求解具有以下性质：

• 最优子结构性质：最优解包含了其子问题的最优解，不是合并所有子问题的解，而是找最优的一条解线路，选择部分子最优解来达到最终的最优解。
• 子问题重叠性质：先计算子问题的解，再由子问题的解去构造问题的解（由于子问题存在重叠，把子问题解记录下来为下一步使用，这样就可以从备忘录中读取）。其中备忘录先记录初始状态。

求解过程

定义一个二维数组m[n][C]，每个元素代表一个状态，m[i][j]表示前 i 个物品放入容量为 j 的背包所能获得的最大价值，我们可以很容易分析得出m[i][j]的计算方法：

• 初始状态：初始状态都为0，表示前0个物品无论放入多大的背包价值都为0，容量为0的背包无论多大价值的物品都无法装进去；

• 转移函数

  if(w(i)>j)
          m[i][j]=m[i-1][j];
  else
          m[i][j]=max(m[i-1][j],m[i-1][j-w(i)]+v(i));
  /* 最后一行代码就是根据“为了容量为C的背包中物品总价值最大化，第i件物品应该放入背包中吗”转化来的。v(i)表示第i件物品的价值，w(i)表示第i件物品的重量。m[i-1][j]表示不将这件物品放进背包的背包的总价值，m[i-1][j-v(i)]+w(i)表示将第i件物品放进背包后背包的总价值，比较两者，取最大值作为最终的选择。 */

假设有6个物品：

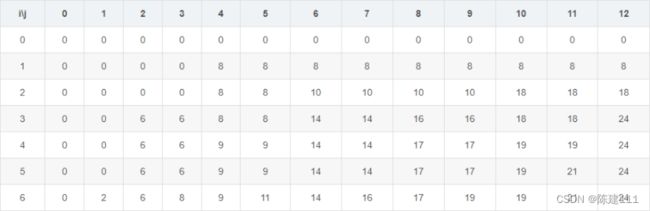
价值数组v = {8, 10, 6, 3, 7, 2}， 重量数组w = {4, 6, 2, 2, 5, 1}， 求背包容量C = 12时对应的m[i][j]数组。

 

代码

package org.cj;

import java.util.Arrays;

public class MyTest1 {
    public static void main(String[] args) {
        MyTest1 myTest1 = new MyTest1();

        int w[] = {2,3,4,5,9}; //物品重量
        int v[] = {3,4,5,8,10}; //物品价值
        int num = w.length;//物品个数为5
        int W = 20; //背包重量
        int table[][] = myTest1.knapsack(W, w, v, num); //计算背包问题最优解的值

        System.out.println("最优解的值："+table[num][W]);

        //输出存储表
        int n = String.valueOf(table[num][W]).length();
        for (int i = 0; i <= num; i++) {
            for (int j = 0; j <= W; j++) {
                System.out.print(String.format(" %"+n+"d", table[i][j]));
            }
            System.out.println("\n");
        }

        System.out.println("最优解为：");
        int[] x = myTest1.knapsackDp(table, W, w, v, num);
        for (int i=0;i c) { //第k件物品放不进去 此时背包的价值 = 判断完上一件物品之后背包的价值
                    table[k][c] = table[k - 1][c];
                } else {
                    int value1 = table[k - 1][c - wTemp[k]] + vTemp[k]; //放入第k件物品后 背包总价值 = 先给这件物品留出空间，剩余的背包大小能装进的最大价值 + 这件物品的价值
                    int value2 = table[k - 1][c]; //不放入第k件物品 背包总价值 = 不用给这件物品留出空间，当前背包大小能装进的最大价值(就是判断完上一件物品之后背包的价值)
                    table[k][c] =  value1 > value2 ? value1:value2;
                }
            }
        }
        return table;
    }

    /**
     * 查找最优解
     * table - 存储表
     * W - 背包重量
     * w - 物品重量
     * v - 物品价值
     * len - 物品个数
     */
    int[] knapsackDp(int table[][], int W, int w[], int v[], int len) {
        int k; // 第k个物品
        int x[] = new int[len];
        //初始化表，将重量和价值数组前面都加上一个0
        int wTemp[] = new int[len+1];
        wTemp[0] = 0;
        System.arraycopy(w,0, wTemp,1,len);
        int vTemp[] = new int[len+1];
        vTemp[0] = 0;
        System.arraycopy(v,0, vTemp,1,len);
        //填表
        for (k=len;k>1;k--) {
            if (table[k][W] == table[k-1][W]) { //重量为W的最优选择的背包中不包含该物品
                x[k-1] = 0;
            }else{ //重量为W的最优选择的背包中包含该物品
                x[k-1] = 1;
                W -= w[k-1];
            }
        }
        if (table[1][W] == 0) { //第一个物品不放入背包
            x[0]=0; 
        } else{ //第一个物品放入背包
            x[0]=1;
        }
        return x;
    }
}

8.5 贪心法

8.5.1 概念

贪心法是一种对某些求最优解问题的更简单、更迅速的技术。用贪心法设计算法的特点是一步一步地进行，常以当前情况为基础根据某个优化测试作最优选择，而不考虑各种的整体情况，它省去了为找最优解要穷尽所有可能而必须耗费的大量时间，它采用自定向下，以迭代的方法做出相继的贪心选择，每做一次贪心选择就将所求的问题化为一个规模更小的子问题，通过每一步的选择，可得到问题的一个最优解，虽然每一步都要保证能获得局部最优解，但由此产生的全局解有时不一定是最优的，所以贪心法不要回溯。

贪心算法基本求解思路：

• 基本思路：
  1. 建立数学模型来描述问题
  2. 把求解的问题分成若干个子问题
  3. 对每一子问题求解，得到子问题的局部最优解
  4. 把子问题的解的局部最优解合成原来求解问题的一个解
• 实现该算法的过程: 从问题的某一初始解触发； while 能朝给定总目标前进异步 do；求出可能的一个解元素；由所有解元素组合成问题的一个可行解。

确定问题能否用贪心策略求解；一般来说，适用于贪心策略求解的问题具有以下特点：

• 贪心选择性质：可通过局部的贪心选择来达到问题的全局最优解。运用贪心策略解题，一般来说需要一步步的进行多次的贪心选择。在经过一次贪心选择之后，原问题将变成一个相似的，但规模更小的问题，而后的每一步都是当前看似最佳的选择，且每一个选择都仅做一次。
• 最优子结构性质：原问题的最优解包含子问题的最优解，即问题具有最优子结构的性质。在背包问题中，第一次选择单位质量最大的货物，它是第一个子问题的最优解，第二次选择剩下的货物中单位重量价值最大的货物，同样是第二个子问题的最优解，依次类推。

public class MyTest3 {
    public static void main(String[] args) {
        MyTest3 myTest1 = new MyTest3();

        int w[] = {35,30,60,50,40,10,25}; //物品重量
        int v[] = {10,40,30,50,35,40,30}; //物品价值
        int W = 150; //背包重量

        myTest1.knapsackGreedy(W, w,v);
    }

    /**
     * 贪婪算法实现背包问题求解
     * @param capacity  背包容量
     * @param weights   各个物品的重量
     * @param values    各个物品的价值
     */
    private void knapsackGreedy(int capacity,int weights[],int values[]) {
        int n=weights.length;   //物品的数量

        Double[] r=new Double[n];  //保存性价比的数组
        int [] index=new int[n]; //保存按性价比排序的物品的下标
        //计算得到各个物品的性价比
        for (int i = 0; i < n; i++) {
            r[i]=(double)values[i]/weights[i];
            index[i]=i;  //初始化各个物品的默认性价比排序
        }

        //对各个物品的性价比进行排序
        for(int i=0;i

8.6 回溯法

8.6.1 回溯法概念

回溯法有"通用的解题法"之称，用它可以系统地搜索一个问题的所有解或任一解。回溯法是一个既带有系统性有带有跳跃性的搜索算法。它在包含问题的所有解空间树中，按照深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。若肯定不包含，则跳过对以该结点为根结点的子树的系统搜索，逐层向其祖先结点回溯；否则就进入该子树，继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时要回溯到根，且根结点的所有子树都已被搜索才结束；而用来求问题的任一解时，只要搜索到问题的一个解就可以结束。这种深度优先的方式系统地搜索问题的解的方法称为回溯法，它适用于解一些组合数较大的问题。

回溯法的算法框架：

1. 问题的解空间

   在应用回溯法解问题时，首先应明确定义问题的解空间。问题的解空间至少包含问题的一个（最优）解。例如，对于n种可选物品的 0-1 背包问题，其解空间由长度为n的 0-1 向量组成。该解空间包含了对变量的所有可能的 0-1 赋值。当 n=3 时，其解空间是{ (0,0,0), (0,1,0), (0,0,1), (1,0,0), (0,1,1), (1,0,1), (1,1,0), (1,1,1) } 。

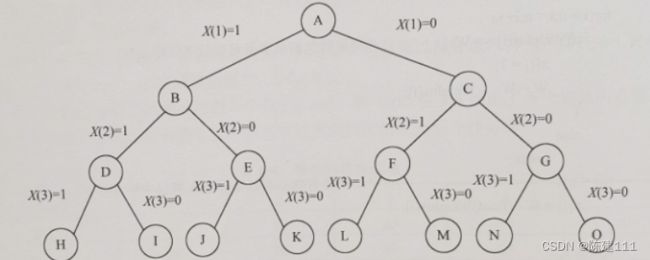
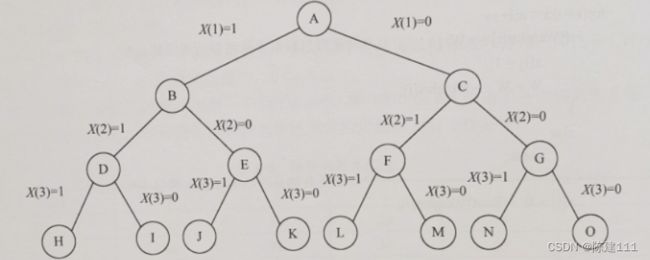
   定义了解空间后，还应将解空间很好地组织起来，使得回溯法能方便地搜索整个解空间。通常将解空间表示为树或图的形式。例如，对于n=3的0-1背包问题，其解空间用一个完全二叉树表示，如下图。

    

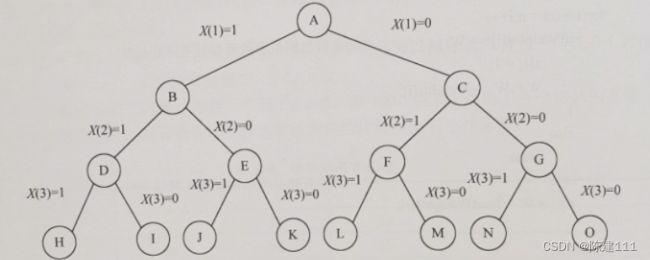
   解空间的第i层到第i+1层边上的标号给出了遍历的值。从树根到叶子的任一路径表示解空间的一个元素。例如，从根结点到结点H对应于解空间中的元素(1,1,1)

2. 回溯法的基本思想

   确定了解空间的组织结构后，回溯法从开始结点（出发），以深度优先的方式搜索整个解空间。这个开始结点就称为一个活结点，同时也称为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移动至一个新结点。这个新节点就成为新的活动结点，并成为当前扩展结点。如果在当前扩展结点处不能再向纵深方向移动，则当前的扩展结点就成为死结点。此时，应该往回移动（回溯）至最新一个活动结点处，并使这个结点成为当前的扩展结点。回溯法即以这种工作方式递归地在解空间中搜索，直到所要求的解或解空间中已无活动结点为止。

   例如，n=3 时的 0-1 背包问题，考虑下面的具体实例：w=[16,15,15]，p=[45,25,25], c=30（w-重量 p-价值 c-背包容量）。从上图的根结点开始搜索其解空间。

   1. 开始时，根结点是活结点，也是当前扩展结点。在这个扩展结点处，按照深度优先移至B或C。假设先移至B，此时 A和B是活结点，结点B成为当前的扩展结点。由于选取了 w1(A到B的边上标记为1)，故在结点B处剩余容量r = 14，获取的价值是45。
   2. 从结点B处可以移至 D 或 E。由于移至结点D 需要 w2=15 的背包让你管理，而现在的容量是14，故移至D 导致一个不可行的解。而搜索至E不需要占用背包容量（结点B到结点E的边上标记为0，表示不需要该物品），因此是可行的。从而选择移至结点E，此时E称为新的扩展结点，结点A、B和E是活结点。在结点 E 处，r=14，获取的戒指为 45。
   3. 从结点E处可以移至结点 J、K。移至J导致一个不可行解，而移至K是可行的，于是移至结点K，它称为一个新的扩展结点。由于结点K是一个叶子结点，故得到一个可行解，这个解对应的价值是45。解 x 的取值是由根结点到叶子结点K路径唯一确定的，即 x = (1,0,0) 。由于在结点K处已不能在向纵深扩展，所以结点K成为死结点。返回到 E，此处E没有可扩展的结点，它也成为了一个死结点。
   4. 返回B处，B同样成为死结点。从而结点A再次成为当前扩展结点。结点A还可以继续扩展，从而达到C。此时r=30，获取的价值为0。
   5. 从结点C可移至 F 或 G 。假设移至 F,它称为新的扩展结点。结点A、C、F是活结点。在结点F处 r=15，获取的价值为 25.从结点F移至 L处，此时r=0，获得的价值为50。由于L是一个叶子结点，而且是迄今为止找到的获取价值最高的可行解，因此记录这个可行解。结点L不可扩展，返回到结点F。

   按此方法继续搜索，可搜索整个解空间。所搜结束后找到的最好解就是 0-1背包问题的最优解。

   综上所述，运用回溯法通常包含以下3个步骤：

   • 针对所给问题，定义问题的解空间
   • 确定易于搜索的解空间结构。
   • 以深度优先的方式搜索解空间。

3. 回溯法的算法框架

   • 非递归方式：

     BackTracking(X)

     1 计算解 X 第一个元素的候选集合 S

     2 k ← 1

     3 while k>0 do

     4 while sₖ ≠ φ do

     5 xₖ ← Sₖ 中的下一个元素

     6 Sₖ ← Sₖ - {xₖ}

     7 if X = {x₁,x₂,...,xₖ} 是问题的解

     8 then 输出 X

     9 k ← k+1

     10 计算解 X 的第 k 个元素的候选集合 Sₖ

     11 k ← k -1

   • 递归方式：

     BackTrackingDFS(X, k)

     1 if X = {x₁,x₂,...,xₖ} 是问题的解

     2 then 输出 X

     3 else k ← k+1

     4 计算解 X 的第 k 个元素的候选集合 Sₖ

     5 while sₖ ≠ φ do

     6 xₖ ← Sₖ 中的下一个元素

     7 Sₖ ← Sₖ - {xₖ}

     8 BackTrackingDFS(X, k)

     9 return

4. 回溯法的界限函数

   问题的解空间往往很大，为了有效地进行搜索，需要在搜索的过程中对某些结点进行剪枝，而对哪些结点进行剪枝，需要设计界限函数来判断。因此，界限函数的设计是回溯法的一个核心问题，也是一个很难的问题。设计界限函数的通用的直到原则是尽可能多和尽可能早地“杀掉”不可能产生最优解的活结点。好的界限函数可以大大减少问题的搜索空间，从而大大提高算法的效率。下面通过例子来说明。

8.6.3 回溯法实例

0- 背包问题 : 给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 wi，其价值为 vi。问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

 

上图已给出 0-1 背包问题的解空间树的示例。在该问题中，目标是为了得到最大价值，因此可以杀掉哪些不可能产生最大价值的活结点。那么，如何判断哪些结点扩展后不能产生最大价值呢？考虑贪心策略，先对物品按其单位重量从大到小排序，对搜索树中的某个节点，如F，已经确定了某些 X(i) ，1≤i≤k，而其他的 X(i)，k+1≤i≤n 待定。此时可以将 0-1 背包问题松弛为背包问题，求从F点扩展下去，计算能获得的最大价值，若该价值比当前已获得某个可行解的值要小，则该结点不扩展。

若所有物品已经按其单位重量价值从大到小排序。假设 k 个物品是否放入背包以及确定，现在考虑在当前背包的剩余容量下，若是背包问题，那么能获得的最大价值是多少？即求背包物品的价值上限。代码如下：

/**
 * 回溯法的01背包
 *
 * @author anLA
 *
 */
public class BagFBack {

    private MyElement[] myelements; // 封装的物品
    private float s; // 背包容量
    private float nowWeight = 0; // 记录当前以拿重量
    private float nowPrice = 0; // 记录当前以拿价格
    private float betterValue; // 记录最多的价格

    /*
     * 构造方法，用于初始化各个变量
     */
    public BagFBack(float[] w, float[] v, float s) {
        myelements = new MyElement[w.length];
        for (int i = 0; i < w.length; i++) {
            myelements[i] = new MyElement();
            myelements[i].v = v[i];
            myelements[i].w = w[i];

        }
        this.s = s;
        // 对数组进行价值排序,系统的是从小到大的，但我讲MyElement改了，使得是从大到小
        Arrays.sort(myelements);
        System.out.println("物品价值" + "    " + "物品重量");
        for (int i = 0; i < myelements.length; i++) {
            System.out.print(myelements[i].v + "    " + myelements[i].w);
            System.out.println();
        }
    }

    public void traceBack(int t) {
        if (t >= myelements.length) {
            // 已经遍历到最下一层，也就是最后一个
            System.out.println("找到方法");
            betterValue = nowPrice;
            System.out.println("最终拿到： " + betterValue);
            output(myelements);
            return;
        }
        // 首先进入走左子树
        if (nowWeight + myelements[t].w < s) {
            // 进入左子树
            nowWeight += myelements[t].w;
            nowPrice += myelements[t].v;
            myelements[t].take = true;
            traceBack(t + 1);
            // 还原现场
            nowWeight -= myelements[t].w;
            nowPrice -= myelements[t].v;
            myelements[t].take = false;
        }

        // 进入右子树，以及要进入的条件
        if (bound(t + 1) > betterValue) {
            traceBack(t + 1);
        }

    }

    // 输出方法，用于输出
    public void output(MyElement[] myelements2) {
        System.out.print("拿重量为这些的物品：");
        for (int i = 0; i < myelements2.length; i++) {
            if (myelements2[i].take) {
                System.out.print(myelements2[i].w + "    ");
            }
        }
    }

    /**
     * 用于计算右边的，如果右边大些，就直接进入
     *
     * @param i
     * @return
     */
    public float bound(int i) {
        // 计算上界
        float cleft = s - nowWeight;
        float bound = nowPrice;
        // 以物品单位价值递减顺序装入物品
        while (i < myelements.length && cleft > myelements[i].v) {
            cleft -= myelements[i].w;
            bound += myelements[i].v;
            i++;
            myelements[i].take = true;
        }

        // // 如果最后一个不能整个放下去,那就装满背包，此问题讨论01背包，要么装，要么不装，所以不用加这一句
        // if (i < myelements.length) {
        // bound += (myelements[i].v / myelements[i].w) * cleft;
        // }
        return bound;

    }

    /**
     * 封装为物品的类
     *
     * @author anLA
     *
     */
    class MyElement implements Comparable {
        float w;
        float v;
        boolean take = false;

        // 更改实现的方法，方便调用系统函数
        @Override
        public int compareTo(Object o) {
            if (v / w < ((MyElement) o).v / ((MyElement) o).w) {
                return 1; // 注意，此处主要用于排序，从大到小排序，所以故意反
            } else {
                return -1;
            }
        }
    }

    public static void main(String[] args) {

        float[] w = { 3.4f, 2.5f, 6f, 4f, 9.0f };
        float[] v = { 3f, 2.5f, 5f, 9f, 6.2f };
        float s = 10;
        BagFBack bagFBack = new BagFBack(w, v, s);
        // 从第0层开始回溯
        bagFBack.traceBack(0);
    }
}

8.7 分支界限法

分支界限法类似于回溯法，也是一种在问题的解空间树T上搜索问题解的算法。但在一般情况下，分支界限法与回溯法的求解目标不同。回溯法的求解是找出T中满足约束条件的所有解，而分支界限法的求解目标是找出满足约束条件的一个解，或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的，即某种意义下的最优解。

由于求解的目标不同，导致分支界限法与回溯法在解空间树 T 上的搜索方式也不同。回溯法以深度优先的方式搜索解空间树 T，而分支界限法以广度优先或以最小耗费方式搜索解空间树 T。分支界限法的搜索策略是每一个活结点只有一次机会成为扩展结点，活动结点一旦称为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，哪些导致不可行解或非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。此后，从活结点表中取下一节点称为当前扩展结点，并重复上述结点扩展过程。这个过程一致持续到找到所需的解或活节点表为空时为止。人们已经利用分支界限法解决了大量离散最优化的实际问题。

与回溯法相似，界限函数的设计是分支界限法的一个核心问题，也是一个很难的问题，如何设计界限函数来有效地减小搜索空间是应用分支界限法要考虑的问题。

根据从活结点表中选择下一扩展结点的不同方式，可将分支界限法分为机制不同的类型。最常用的有两种：

1. 队列式（FIFO，先进先出）分支界限法。队列式分支界限法将活结点表组织成一个队列，并按队列的先进先出原则选择下一个节点作为扩展结点。
2. 优先队列式分支界限法。优先队列式分支界限法将活结点表组织成一个优先队列，并按优先队列中规定的结点优先级选择优先级高的下一个节点作为扩展结点。

优先队列中规定的优先级通常用一个与该节点相关的数值p来表示。节点优先级的高低与 p 相关。最大优先队列规定 p 值较大的节点优先级较高。在算法实现时，通常用一个最大堆起来实现最大优先队列，用最大堆的 Deletemax 操作抽取堆中下一个节点称为当前扩展结点。类似的，最小队列规定 p 值较小的节点优先级较高。在算法实现时，通常用一个最小堆起来实现最小优先队列，用最小堆的 Deletemin 操作抽取堆中下一个节点称为当前扩展结点。

例如 n=3 时，0-1 背包问题的一个实例： w=[16,15,15]，p=[45,25,25]，c=30，其解空间如图：

 

用队列分支界限法解此问题时，用一个队列来存储活结点表。算法从根节点A触发。

1. 初始时活结点队列为空。
2. 结点A是当前扩展结点，它的儿子 B 和 C 均为可行节点，故将这两个儿子结点按从左到右的顺序加入活动结点队列，并舍弃当前扩展结点A。
3. 按照先进先出原则，下一个扩展结点是B。扩展结点B得到儿子 D和E。由于D是不可行的，故被舍去。E是可行节点，被加入活结点列表。此时活结点队列中的元素是C和E。
4. C为当前的扩展结点，它的两个儿子结点F、G均为可行节点，因此被加入活结点队列。此时活结点队列的元素是 E、F、G。
5. 扩展下一个节点E，得到 J、K。J是不可行节点，因而被社区。K是一个可行的叶子结点，表示所求问题是一个可行解，其价值为45。此时活结点队列中的元素是F和G。
6. F成为下一个扩展结点。它的两个儿子 L 和 M 均为叶子节点。L表示获得价值为50的可行解，M 表示获得截止为 25 的可行解。
7. F是最后一个扩展结点。它的两个儿子 N 和 O 均为叶子节点。最后活结点队列为空，算法终止。算法搜索得到最优解的值为50，对应的解为(0,1,1)。

8.8 概率算法

前面讨论的算法对于所有合理的输入都给出正确的输出，概率算法将这一条件放宽，把随机性的算则加入到算法中。在算法执行某些步骤时，可以随机地选择下一步该如何进行，同时允许结果以较小的概率出现错误，并以此为代价，获得算法运行时间的大幅度减少。概率算法的一个基本特征是对所求解问题的同一实例用同一概率算法求解两次，可能得到完全不同的效果。这两次求解所需时间甚至所得到的的结果可能会有相当大的差别。如果一个问题没有有效的确定型算法可以在合理的时间内给出解，但是该问题能接受小概率错误，那么采用概率算法就可以快速找到这个问题的解。

一般情况下，概率算法具有以下基本特征：

1. 概率算法的输入包括两部分，一部分是原问题的输入，另一部分是供算法进行随机选择的随机数序列。
2. 概率算法在运行的过程中，包括溢出或多处随机算则，根据随机值来决定算法的运行路径。
3. 概率算法的结果不能保证一定是正确的，但能限制其出错概率。
4. 概率算法在不同的运行过程中，对于相同的输入实例可以有不同的结果，因此，对于相同的输入实例，概率算法的执行时间可能不同。

概率算法大致分为4类：数值概率算法、蒙特卡罗算法、拉斯维加斯算法和舍伍德算法。

1. 数值概率算法常用于数值问题的求解。这类算法得到的往往是近似解，且近似解的精度随计算时间的增加不断提高。在多数情况下，要计算出问题的精确解是不可能的，因此数值概率算法可得到相当满意的解、。
2. 蒙特卡罗算法用于求问题的精确解。用蒙特卡罗算法能求得问题的一个解，但这个解未必是正确的。求得正确的概率依赖于算法所用的时间，时间越长，得到正确接的概率越高。蒙特卡罗算法的主要缺点在于此，一般情况下，无法有效地判定所得到的解是否肯定正确。
3. 拉斯维加斯算法不会得到不正确的解。一旦拉斯维加斯算法找到一个解，这个解一定是正确解。拉斯维加斯算法找到正确解的概率随他所用的计算机时间的增加而提高。对于所求解问题的任一实例，用同一拉斯维加斯算法反复对该实例求解足够多次，可使求解失效的概率任意小。
4. 舍伍德算法总能求得问题的一个解，且所求的的解是正确的。当一个确定型算法在最坏情况下的计算复杂度与其在平均情况下的计算复杂度有较大差别时，可在这个确定性算法中引入随机性将他改造成一个舍伍德算法，消除或减少问题的好坏实例间的这种差别。舍伍德算法算法的精髓不是避免算法的最坏情况行为，而是设法消除这种最坏情形行为与特定实例之间的关联性。

8.9 近似算法

迄今为止，所有的难解问题都没有多项式时间算法，采用回溯法和分支界限法等算法设计技术可以相对有效的解决这类问题。然而，这些算法的时间性能常常是无法保证的。近似算法是解决难解问题的一种有效策略，其基本思想是放弃求最优解，而用近似最优解代替最优解，以换取算法设计上的简化和时间复杂度的降低。近似算法是这样一个过程“虽然它可能找不到一个最优解，但它总会给带求解的问题提供一个解。为了具有实用性，近似算法必须能够给出算法所产生的解与最优解之间的差别或者比例的一个界限，它保证任意一个实例的近似最优解与最优解之间相差的程度。显然，这个差别越小，近似算法越具有实用性。

衡量近似算法性能最重要的标准有以下两个：

1. 算法的时间复杂度。近似算法的时间复杂度必须是多项式阶的，这是近似算法的基本目标。
2. 解的近似程度。近似最优解的近似程度也是设计近似算法的重要目标。近似程度与近似算法本身、问题规模，乃至不同的输入实例有关。

8.10 数据挖掘算法

在当今的大数据时代，数挖掘、机器学习和人工智能这些名词在我们的生活、工作和学习中已经是耳熟能详的词汇。我们需要各种技术来分析爆炸式增长的各类数据，以发现隐含在这些数据中有价值的信息和知识。作为一门交叉学科，数据挖掘利用机器学习方法对多种数据，包括数据库、数据仓库数据、Web数据等进行分析和挖掘。数据挖掘的核心是算法，其主要功能包括分类、回归、关联规则和聚类等。

8.11 智能优化算法

优化技术是一种以数学为基础，用于求解各种工程问题优化解的应用技术。作为一个重要的科学分支，它一直受到人们的广泛重视，并在诸多工程领域迅速得到推广和应用，如系统控制、人工智能、识别模式、生产调度、VLSI技术和计算机工程等。鉴于实际工程问题的复杂性、约束性、非线性、多级小、建模困难等难点，寻求一种适合于大规模并具有智能特征的算法是一个主要目标和研究方向。20世纪80年代以来，一些新颖的优化算法，如人工神经网络、混沌、遗传算法、进化规划、模拟退货、紧急搜索机器混合花策略等，通过某些自然现象或过程而发展得到，其思想和内容设计数学、物理学、生物进化、人工智能、神经科学和统计学等方面，为解决复杂问题提供了思路和手段。