【鲁棒电力系统状态估计】基于投影统计的电力系统状态估计的鲁棒GM估计器(Matlab代码实现)
欢迎来到本博客❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
本文目录如下:
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码实现
1 概述
稳健的电力系统状态估计器对于监测和控制应用至关重要。根据我们的经验,我们发现使用投影统计的鲁棒广义最大似然(GM)估计器是文献中最好的方法之一。它对多个交互和符合不良数据、不良杠杆点、不良零注入以及某些类型的网络攻击具有鲁棒性。此外,它的计算效率很高,使其适用于在线应用程序。除了GM估计器良好的击穿点外,它在高斯或其他厚尾非高斯测量噪声下具有很高的统计效率。使用SCADA测量的GM估计器的原始版本是由Mili和他的同事在1996年提出的[1]。通过在 [R2] 中使用吉文斯旋转,其数值稳定性得到了增强。在[R3]中,GM估计器被扩展为同时估计变压器抽头位置和系统状态。不良的零点注入也得到了解决。在[R4]中,提出了GM估计器来处理创新和观测异常值以及动态状态估计中的测量损失。测试系统包括 IEEE 14 总线、30 总线和 118 总线系统。仅包括 SCADA 测量值。
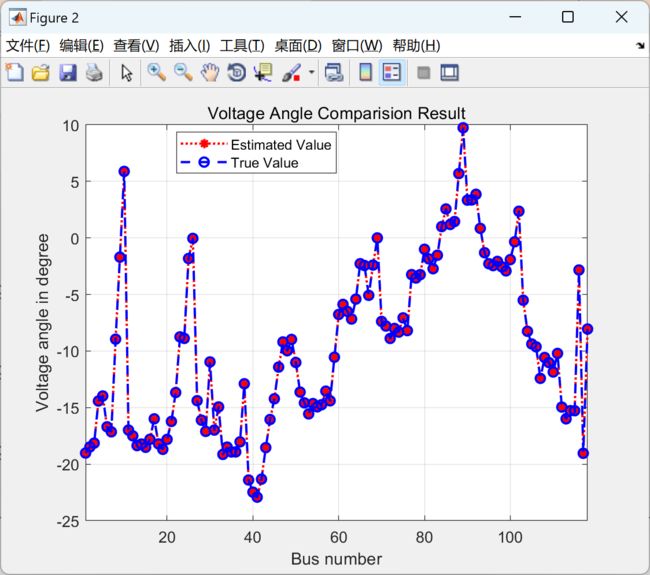
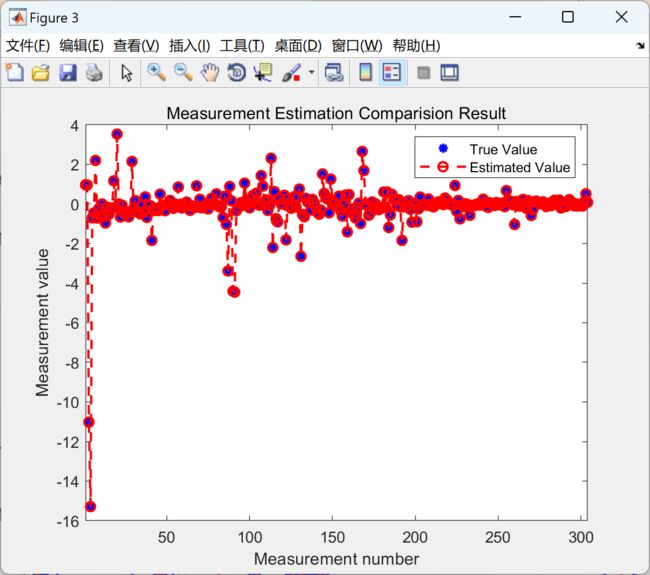
由于结果图比较多,本文仅展现IEEE118节点运行结果图。
2 运行结果
部分代码:
zdata = zconv(nbus); % Get Conventional Measurement data..
[bsh g b] = line_mat_func(nbus); % Get conductance and susceptance matrix
type = zdata(:,2);
% Type of measurement,
% type =1 voltage magnitude p.u
% type =2 Voltage phase angle in degree
% type =3 Real power injections
% type =4 Reactive power injection
% type =5 Real power flow
% type =6 Reactive power flow
z = zdata(:,3); % Measurement values
Z=z;% for ploting figures
fbus = zdata(:,4); % From bus
tbus = zdata(:,5); % To bus
Ri = diag(zdata(:,6)); % Measurement Error Covariance matrix
e = ones(nbus,1); % Initialize the real part of bus voltages
f = zeros(nbus,1);% Initialize the imaginary part of bus voltages
E = [f;e]; % State Vector comprising of imaginary and real part of voltage
G = real(ybus);
B = imag(ybus);
ei = find(type == 1); % Index of voltage magnitude measurements..
fi = find(type == 2); % Index of voltage angle measurements..
ppi = find(type == 3); % Index of real power injection measurements..
qi = find(type == 4); % Index of reactive power injection measurements..
pf = find(type == 5); % Index of real power flow measurements..
qf = find(type == 6); % Index of reactive power flow measurements..
Vm=z(ei);
Thm=z(fi);
z(ei)=Vm.*cosd(Thm); % converting voltage from polar to Cartesian
z(fi)=Vm.*sind(Thm);
nei = length(ei); % Number of Voltage measurements(real)
nfi = length(fi); % Number of Voltage measurements(imaginary)
npi = length(ppi); % Number of Real Power Injection measurements..
nqi = length(qi); % Number of Reactive Power Injection measurements..
npf = length(pf); % Number of Real Power Flow measurements..
nqf = length(qf); % Number of Reactive Power Flow measurements..
nm=nei+nfi+npi+nqi+npf+nqf; % total number of measurements
% robust parameters
tol=1;
maxiter=30;% maximal iteration for iteratively reweighted least squares (IRLS) algorithm
c=1.5; % for Huber-estimator
bm=mad_factor(nm); % correction factor to achieve unbiasness under Gaussian measurement noise
%%%%%%% GM-estimator%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% flat initialization
iter=1;
s=1;
%% For the GM-estimator to be able to handle two conforming outliers located on the same bus
%% the local redundancy must be large enough
%% add outliers %%
3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[R1] L. Mili, M. Cheniae, N. Vichare, and P. Rousseeuw, ``Robust state estimation based on projection statistics," IEEE Trans. Power Syst, vol. 11, no. 2, pp. 1118--1127, 1996.
[R2] R. C. Pires, A. S. Costa, L. Mili, "Iteratively reweighted least-squares state estimation through givens rotation," IEEE Trans. Power Syst., Vol. 14, no. 4, pp. 1499--1507, 1999.
[R3] R. C. Pires, L. Mili, F. A. Becon Lemos, ``Constrained robust estimation of power system state variables and transformer tap positions under erroneous zero-injections," IEEE Trans. Power Syst., vol. 29, no. 3, pp. 1144--1152, May 2014.
[R4] J. B. Zhao, M. Netto, L. Mili, "A robust iterated extended Kalman filter for power system dynamic state estimation", IEEE Trans. Power Syst., DOI:10.1109/TPWRS.2016.2628344, in press.