顺序栈和链栈的初始化，出栈，进栈的具体实现(new和exit的用法)

一 . 栈的定义和特点

栈的基本操作是线性表基本操作的子集，是操作受限的线性表。
**栈（stack）**是限定仅在表尾进行插入或删除操作的线性表。
对于栈来说，表尾端有其特殊含义，称为栈顶(top)，相应地，表头为栈底(bottom)。
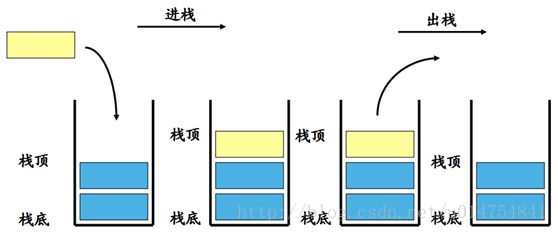
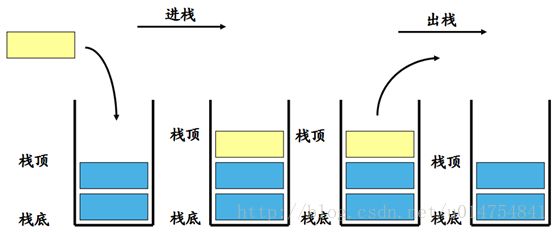
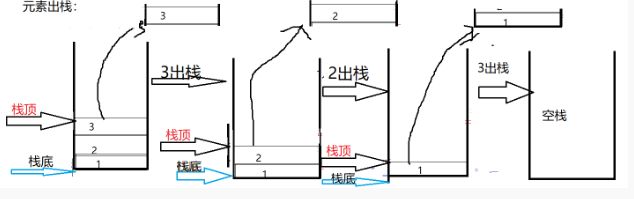
栈又称为后进先出(Last In First Out,LIFO)的线性表。
栈主要分为静态栈和动态栈，静态栈类似于数组，而动态栈类似于链表，但只能对链表的一端进行操作。
顺序栈：

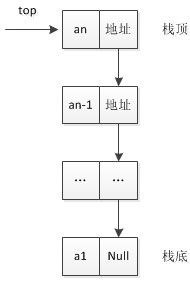
链栈：

二 . 栈的抽象类型定义

ADT 栈(STACK)
{
	DATA
		同线性表。元素具有相同的类型，相邻元素具有前驱后继关系。
	OPERATION
		InitStack(&S)	    构造一个空栈S
		DsetroyStack(&S)	若栈存在，销毁栈
		ClearStack(&S)   	将栈清空
		StackEmpty(S)	    若栈存在元素返回False，否则返回True
		GetTop(S)	        得到栈顶数据元素
		Push(&S,e)	        若栈存在，将新元素e插入到栈顶
		Pop(&S,&e)       	删除栈顶元素，并用e返回其值
		StackLength(S)	    返回栈的元素个数
		StackTraverse(S)	从栈底到栈顶依次对S的每个数据元素进行访问		
} 

三 . 顺序栈的基本操作

1 . 顺序栈的定义

顺序栈是指利用顺序存储结构实现的栈，即利用一组连续的存储单元依次存放自栈底到栈顶的数据元素，同时附带指针top指示栈顶元素在顺序栈中的位置。

#define MAXSIZE 10		//顺序栈存储空间的初始分配量
typedef struct{
	SElemType *base;	//栈底指针
	SElemType *top;		//栈顶指针
	int longth;			//栈可用的最大容量
}SqStack;

2 . 初始化

顺序栈的初始化操作就是为顺序栈动态分配一个预定义大小得到数组空间。

【算法步骤】

• 为顺序栈动态分配一个最大容量为MAXSIZE的数组空间，是base指向这段空间的基地址，即栈底。
• 栈顶指针top初始为base，表示栈为空。
• longth置为栈的最大容量MAXSIZE。

【算法描述】

 bool  InitStack(SqStack &S) {	//构造一个空栈s
	S.base = new int[MAXSIZE];	//为顺序栈动态分配一个最大容量为MAXSIZE的数组空间
	if (S.base)	exit(-2);		//存储分配失败
	S.top = S.base;				//top初始base,空栈
	S.length = MAXSIZE;			//longth置为栈的最大容量MAXSIZE
	return 1;
}

new和exit的用法

new的用法：

https://blog.csdn.net/zcawesome/article/details/78777832?utm_source=app3

exit的用法：

在C语言的main函数中我们通常使用return 0；exit(0) 表示程序正常退出,exit⑴/exit(-1）表示程序异常退出。exit() 结束当前进程/当前程序/，在整个程序中，只要调用 exit ，就结束。但在如果把exit用在main内的时候无论main是否定义成void返回的值都是有效的，并且exit不需要考虑类型，exit⑴等价于return 1;。

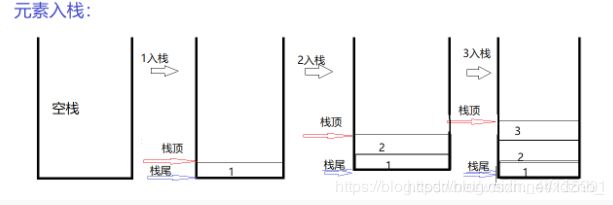
3 . 入栈（压栈）

入栈操作直至在栈顶插入一个新的元素。

【算法步骤】

• 判断栈是否满，若满则返回ERROR。
• 将新元素压入栈顶，栈顶指针加1.

【算法描述】

Status Push(SqStack &S, SElemType e) {			  //插入元素e为新的栈顶元素
	if (S.top - S.base == S.length)	return ERROR; //栈满
	*S.top++ = e;								  //元素e压入栈顶，栈顶指针加1
	return OK;
}

4 . 出栈

出栈操作是将栈顶元素删除
【算法步骤】

• 判断栈是否为空，若空则返回ERROR。
• 栈顶指针减1，栈顶元素出栈。
  

【算法描述】

Status Pop(SqStack &S, SElemType &e) {			 //删除S的栈顶元素，用e返回其值
	if (S.top - S.base == S.length)	return ERROR;//栈空
	e = *--S.top;								 //栈顶指针减1，将栈顶元素付给e
	return OK;
}

5 . 取栈顶元素

当栈非空时，此操作返回当前栈顶元素的值，栈顶指针保持不变。

【算法描述】

SElemType GetTop(SqStack S) {//返回S的栈顶元素，不修改栈顶指针
	if (S.top != S.base)	 //栈非空
		return *(S.top - 1);//返回值栈顶元素的值，栈顶指针不变
}

由于顺序栈和顺序表一样，受到最大容量的限制，虽然可以在”满员“时重新分配空间扩大容量，但工作量较大，应尽量避免。

四 . 链栈的基本操作

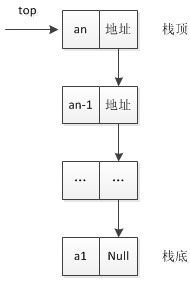
1 . 链栈的定义

链栈时指采用链式存储结构实现的栈。通常用单链表表示

typedef struct StackNode {
	ElemType  date;
	struct StackNode *next;
}StackNode,*LinkStack;

2 . 初始化

l链栈的初始化操作就是构造一个空栈，因为没必要设头结点，所以直接将栈顶指针置空即可。

【算法描述】

Status InitStack(LinkStack &S) {
	S = NULL:
	return OK;
}

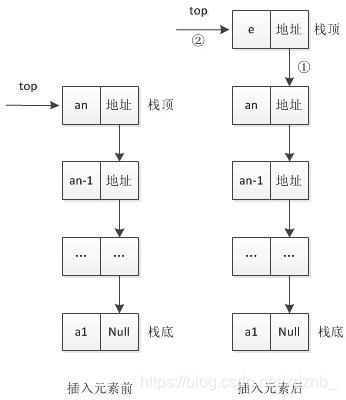
3 . 入栈

链栈不需要判断栈是否满，只需要为入栈元素动态分配一个节点空间。

【算法步骤】

• 为入栈元素e分配空间，用指针p指向。将新结点数据域置为e。
• 将新结点插入栈顶。
• 修改栈顶指针为p。

【算法描述】

Status Push(LinkStack &S, SElemType e) {
	p = new StackNode;		//生成新的结点
	p->data = e;			//将新的数据域结点为e
	p->next = S;			//将新的结点插入栈顶
	S = p;					//修改栈顶指针为p
	return OK;
}

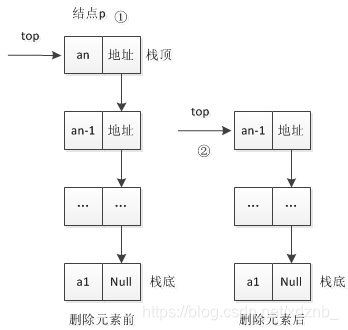
4 . 出栈

l链栈出栈前需要判断栈是否为空，链栈出栈前需要释放栈顶元素。

【算法步骤】

• 判断栈是否为空，若空则返回ERROR
• 将栈顶元素赋给e
• 临时保存栈顶元素空间，以备释放
• 修改栈顶指针，指向新的栈顶元素
• 释放原栈顶元素空间
  
  【算法描述】

Status Pop(LinkStack &S, SElemType &e) {//删除S的栈顶元素，用e返回其值
	if ((S == NULL))	return ERROR;   //栈空
	e = S->data;						//将栈顶元素赋给e
	p = S;								//用p临时保存栈顶元素空间，以备释放
	S = S->next;						//修改栈顶指针
	delete p;							//释放原栈顶元素空间
	return OK;
}

5 . 取栈顶元素

当栈非空时，此操作返回当前栈顶元素的值，栈顶指针S保持不变。

【算法描述】

SElemType GetTop(LinkStack S) {//返回S的栈顶指针，不修改栈顶的指针
	if (S != NULL)			   //栈非空
		return S->data;		   //返回栈顶元素的值，栈顶指针不变
}

五 . 顺序栈操作的实现

#include
using namespace std;
#define MAXSIZE 10
typedef struct Stack{
	int  *top;
	int *base;
	int length;
}SqStack;
bool InitStack(SqStack &S){
	
	S.base = new int[MAXSIZE];
	if (!S.base)	exit(-2);
	S.top = S.base;
	S.length = MAXSIZE;
	return 1;
}
bool Push(SqStack &S, int e) {
	if (S.top - S.base == S.length)	return 0;
	*(S.top++) = e;
	return 1;
}
int Pop(SqStack &S) {
	int e;
	if (S.top  == S.base)	return 0;
	e = *(--S.top);
	return e;
}
int GetTop(SqStack S){
	if (S.top != S.base)
		return *(S.top - 1);
}
int  main() {
	SqStack S;
	int e;
	cout << "创建顺序栈" << endl;
	if (InitStack(S))
		cout << "创建顺序栈成功" << endl;
	else cout << "创建失败" << endl;

	cout << "1 . 入栈" << endl;
	cout << "输入入栈数字" << endl;
	for (int i = 0; i < 10; i++) {
		cin >> e;
		Push(S, e);
	}
	cout << "2 . 出栈" << endl;
	if (S.base == S.top)
		cout << "栈空" << endl;
	else
		cout << Pop(S) << endl;
	cout << "3 . 取出栈顶元素" << endl;
	cout << GetTop(S) << endl;
	cout << "将所剩元素出栈" << endl;
	for (int i = 0; i < 9; i++) {
		if (S.base == S.top)
			cout << "栈空" << endl;
		else
			cout << Pop(S) << " ";
	}
	cout << endl  << "出栈" << endl;
	if (S.base == S.top)
		cout << "栈空" << endl;
	else
		cout << Pop(S) << endl;
	return 0;
}

六 . 链栈基本操作的实现

#include
using namespace std;
typedef struct StackNode {
	int  data;
	struct StackNode *next;
}StackNode,*LinkStack;
bool InitStack(LinkStack &S) {
	S = NULL;
	return 1;
}
bool Push(LinkStack &S,int e) {
	StackNode *p;
	p = new StackNode;
	p->data = e;
	p->next = S;
	S = p;
	return 1;
}
int Pop(LinkStack &S) {
	int e;
	StackNode *p;
	p = new StackNode;
	if ((S == NULL))	return 0;
	e = S->data;
	p = S;
	S = S->next;
	delete p;
	return e;
}
int GetTop(LinkStack S) {
	if (S != NULL)
		return S->data;
}
int main() {
	int e;
	LinkStack S;
	cout << "创建链栈" << endl;
	if (InitStack(S))
		cout << "创建成功" << endl;
	cout << "1 . 入栈" << endl;
	cout << "输入入站元素" << endl;
	for (int i = 0; i < 10; i++) {
		cin >> e;
		Push(S, e);
	}
	cout << "2 . 出栈" << endl;
	if (S == NULL)
		cout << "栈空" << endl;
	else
		cout << Pop(S) << endl;
	cout << "3 . 取出栈顶元素" << endl;
	cout << GetTop(S) << endl;
	cout << "将所剩元素出栈" << endl;
	for (int i = 0; i < 9; i++) {
		if (S == NULL)
			cout << "栈空" << endl;
		else
			cout << Pop(S) << " ";
	}
	cout << endl <<"出栈" << endl;
	if (S == NULL)
		cout << "栈空" << endl;
	else
		cout << Pop(S) << endl;
	
	return 0;
}