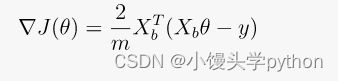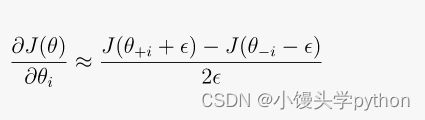深入探讨梯度下降：优化机器学习的关键步骤（三）

引言

随机梯度下降是一种优化方法，主要作用是提高迭代速度，避免陷入庞大计算量的泥沼。在每次更新时，随机梯度下降只使用一个样本中的一个例子来近似所有的样本，来调整参数，虽然不是全局最优解，但很多时候是可接受的。

前两篇主要介绍了一下批量梯度下降，本节前部分主要介绍一下随机梯度下降

---

随机、批量梯度下降的差异

随机梯度下降和批量梯度下降都是常用的优化方法，它们在处理大规模数据集时都有自己的优点和缺点。以下是它们的不同点：

• 相同点：
  两种方法都用于优化目标函数，通过迭代地更新参数来最小化目标函数。在每一步迭代中，它们都会根据当前参数的梯度来更新参数。

• 不同点：
  （1）样本的使用方式：在随机梯度下降中，每次迭代只使用**一个样本**来计算梯度；而在批量梯度下降中，每次迭代会使用整个数据集来计算梯度。因此，随机梯度下降在处理大规模数据集时更高效，因为它不需要加载整个数据集到内存中。

  （2）收敛速度：由于随机梯度下降每次只使用一个样本来计算梯度，因此它的收敛速度通常比批量梯度下降更快。但是，随机梯度下降的收敛可能更加波动，因为每次迭代的样本可能不同。

  （3）准确度：批量梯度下降的准确度通常比随机梯度下降更高。因为批量梯度下降会使用整个数据集来计算梯度，因此它的更新更精确。但是，在处理大规模数据集时，批量梯度下降可能会遇到内存不足的问题。

这里可以通过下列图来进行简单的说明

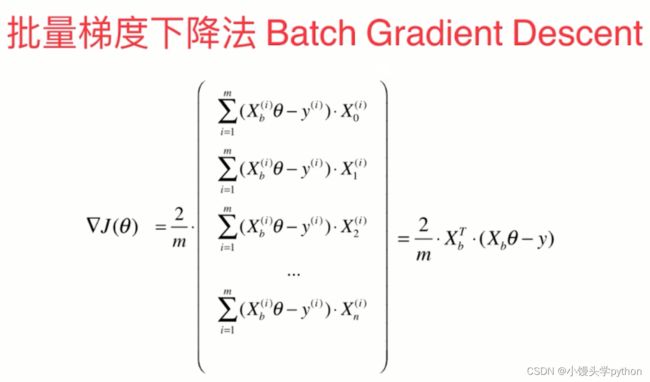
上面这种图是批量梯度下降的主要公式，前两篇文章已经介绍了

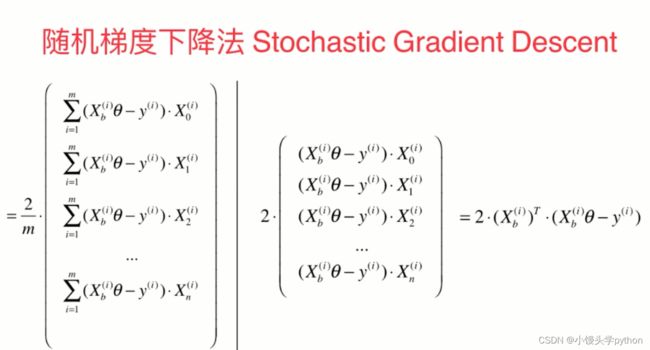
上面的这张图指的就是随机梯度下降的主要公式了，我们可以看到求个符号消失了

随机梯度下降的实现

导入必要的库

import numpy as np

选取100000个数据作为测试数据

m = 100000
x = np.random.random(size=m)
y = x*3+4+np.random.normal(size=m)  # 后面的添加的噪音

注意：后面加了一个噪音目的是使得原有的数据添加一些随机性，省的太假了~
之后我们需要编写两个函数，前一个函数主要是用来计算样本的梯度，后一个函数主要包括计算学习率以及循环判断

def sgd(X_b,y,initial_theta,n_iters,epsilon=1e-8):
    def learning_rate(i_iter):
        t0=5
        t1 = 50
        return t0/(i_iter+t1)
    theta = initial_theta
    i_iter = 1
    while i_iter<=n_iters:
        index=np.random.randint(0,len(X_b))
        x_i = X_b[index]
        y_i = y[index]
        gradient = dj_sgd(theta,x_i,y_i)
        theta = theta-gradient*learning_rate(i_iter)
        i_iter+=1
    return theta

注意：在学习率的计算采用模拟退火思想，目的是为了控制参数的变化来影响行为，从而达到更好的优化效果。

之后我们需要使用numpy库中的hstack函数在x左侧添加一列

X_b = np.hstack([np.ones((len(x),1)),x])  # 左测增加一列

在添加前，我们需要将x转成矩阵

x = x.reshape(-1,1)

运行结果如下

之后我们需要设置initial_theta初始值

initial_theta = np.zeros(X_b.shape[1])

前提的准备做完就可以验证了

%%time 
sgd(X_b,y,initial_theta,n_iters=m//4)

运行结果如下

返回的值，分别近似截距和系数

---

我们可以将代码再优化一下

def sgd(X_b, y, initial_theta, n_iters, epsilon=1e-8):
    def learning_rate(i_iter):
        t0 = 5
        t1 = 50
        return t0 / (i_iter + t1)

    theta = initial_theta  # 初始化模型参数
    m = len(X_b)  # 样本数量

    for cur_iter in range(n_iters):  # 迭代n_iters次，每轮迭代看一遍整个样本
        random_indexs = np.random.permutation(m)  # 随机打乱样本的顺序，用于随机梯度下降
        X_random = X_b[random_indexs]  # 打乱后的特征数据
        y_random = y[random_indexs]  # 打乱后的标签数据

        for i in range(m):  # 遍历每个样本
            # 使用学习率learning_rate(cur_iter*m+i)来更新模型参数theta，通过梯度dj_sgd计算
            theta = theta - learning_rate(cur_iter * m + i) * dj_sgd(theta, X_random[i], y_random[i])

    return theta  # 返回优化后的模型参数

这个函数使用了随机梯度下降算法来更新模型参数，通过不断地随机选择一个样本进行参数更新，逐渐优化模型以适应训练数据。学习率随着迭代次数变化，初始较大然后逐渐减小，以有利于收敛到最优解。

---

随机梯度下降的调试

首先还是做前期的准备

import numpy as np
X = np.random.random(size=(1000,10))
X_b = np.hstack([np.ones((len(X),1)),X])
true_theta = np.arange(1,12,dtype='float') # 这里代表有11个特征值（10个系数，1个截距）
y = X_b.dot(true_theta) + np.random.normal(size=len(X))

之后我们分别才有两种方法进行调试
首先是dj_math

这个函数用于计算线性回归中的成本函数（通常是均方误差）相对于参数 theta 的梯度，采用了矢量化的方法。这是数学公式：

• X_b 是包含偏置项的特征矩阵（通常是原始特征矩阵的一列加上全部为 1 的列）。
• y 是目标向量。
• theta 是待更新的参数向量。
• m 是训练样本的数量。

def dj_math(theta,X_b,y):
    return X_b.T.dot(X_b.dot(theta)-y)*2./len(X_b)

其次是dj_debug

这个函数使用数值逼近方法来计算成本函数相对于参数的梯度。它通过轻微地扰动每个参数 theta[i] 并测量成本函数 j 的变化来估计梯度。这是数学公式：

• theta 是参数向量。
• X_b 是包含偏置项的特征矩阵。
• y 是目标向量。
• i 是被扰动的参数的索引。
• epsilon 是用于扰动的小值。

def dj_debug(theta,X_b,y):
    res=np.empty(len(theta))
    epsilon = 0.01
    for i in range(len(theta)):
        theta1 = theta.copy()
        theta2 = theta.copy()
        theta1[i] +=epsilon
        theta2[i] -=epsilon
        res[i] = (j(theta1,X_b,y)-j(theta2,X_b,y))/(2*epsilon)
    return res

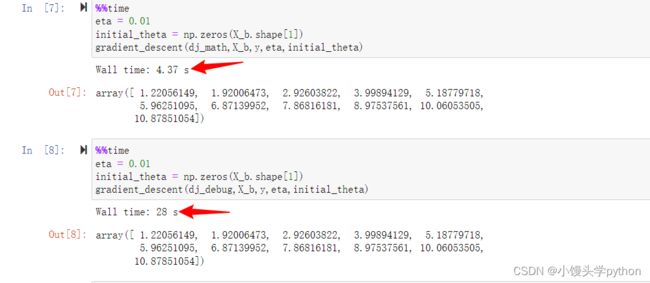
这种数值逼近通常用于调试和验证梯度计算的正确性，特别是在梯度下降等基于梯度的优化算法中，有助于优化参数 theta 的训练过程

完整代码如下

def j(theta,X_b,y):
    try:
        return np.sum((X_b.dot(theta)-y)**2)/len(X_b)
    except:
        return float('inf')

def dj_math(theta,X_b,y):
    return X_b.T.dot(X_b.dot(theta)-y)*2./len(X_b)

def dj_debug(theta,X_b,y):
    res=np.empty(len(theta))
    epsilon = 0.01
    for i in range(len(theta)):
        theta1 = theta.copy()
        theta2 = theta.copy()
        theta1[i] +=epsilon
        theta2[i] -=epsilon
        res[i] = (j(theta1,X_b,y)-j(theta2,X_b,y))/(2*epsilon)
    return res


def gradient_descent(dj,X_b,y,eta,initial_theta,n_iters=1e4,epsilon=1e-8):
    theta = initial_theta
    i_iter = 1
    while i_iter<n_iters:
        last_theta = theta
        theta =theta- eta*dj(theta,X_b,y)
        if abs(j(theta,X_b,y)-j(last_theta,X_b,y))<epsilon:
            break
        i_iter+=1
    return theta

可以分别进行测试一下，显然前者更快一点

—

挑战与创造都是很痛苦的，但是很充实。