射线法——判断一个点是否在多边形内部（适用于凸多边形和凹多边形）【关键原理解释+文字伪代码+java代码实现】

问题介绍

给定一个点和一个多边形（由点集的点依次连接构成），需要判断该点是否在多边形的内部。

方法简述

要判断一个点是否在多边形内部，只需要从点出发，水平向右做一条射线，然后计算射线与多边形的交点数量。若交点数量为偶数，则点在多边形外部；若交点数量为奇数，则点在多边形内部。

计算交点数量

计算交点的方法主要有以下三种：

1. 射线直接与某一条边相交（非边的端点）
2. 射线与两条边的交点相交
3. 射线与一条边有重合片段（边的斜率为0，且y轴坐标与射线的y轴坐标相等）
   

图1 交点类型

要判断出上面的左拐、右拐情况，需要借助向量叉乘

图2 判断左右拐

一般多边形可以由一个点集合表示，点集合中的各个点按照顺序相连即可形成多边形

图3 连接点集得到多边形

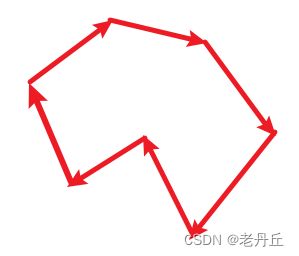
遍历过程

for (int i = 0; i < pointList.size(); i++) {
    //多边形线1(line2）：pointI-pointIPlus1; 
    //多边形线2(line3)：pointIPlus1-pointIPlus2;
    //多边形线3(line4)：pointIPlus2-pointIPlus3
    Point pointI = pointList.get(i);
    Point pointIPlus1 = pointList.get((i + 1) % pointList.size());
    Point pointIPlus2 = pointList.get((i + 2) % pointList.size());
    Point pointIPlus3 = pointList.get((i + 3) % pointList.size());
    
    if(射线与line2相交){
        直接把相交点数+1
    }eles if(pointIPlus1在射线上面){
        if(pointIPlus2不在射线上面){
            判断是否满足图1的第二种情况，满足则交相交点+1
        }else{
            判断是否满足图1的第三种情况，满足则交相交点+1
        }
    }

}

注意点

图4 不可以+1的情况

代码实现

【Point】

package com.ruoyi.algorithm.common.entity;

import lombok.Data;

import java.io.Serializable;
import java.util.ArrayList;
import java.util.List;

@Data
public class Point implements Serializable, Cloneable {

   private static final long serialVersionUID = 1L;
   private String id;
   /**
    * 这个属性没啥用，我主要是用y、z，懒得修改了
    */
   private double x;
   private double y;
   private double z;

   public Point() {
   }

   public Point(double x, double y, double z) {
       this.x = x;
       this.y = y;
       this.z = z;
   }

   @Override
   public Point clone() throws CloneNotSupportedException {
       return (Point) super.clone();
   }

   public static ArrayList<Point> cloneList(List<Point> pointList) throws CloneNotSupportedException {
       ArrayList<Point> clone = new ArrayList<>();
       for (Point point : pointList) {
           clone.add(point.clone());
       }
       return clone;
   }
}

【PointUtil 】

package com.ruoyi.algorithm.get_maximumArea_rectangles_in_a_simple_polygon.version.v1;


import com.ruoyi.algorithm.common.entity.Point;

import java.util.List;


public class PointUtil {

   /**
    * 判断两个点是否相等
    */
   public static boolean judgeWhetherTwoPointsIsSame(Point p1, Point p2) {
       if (p1 == null || p2 == null) {
           return false;
       }
       if (MathUtil.getDistanceOfTwoPoint(p1.getY(), p1.getZ(), p2.getY(), p2.getZ()) < 0.0001) {
           return true;
       } else {
           return false;
       }
   }

}

【MathUtil】

package com.ruoyi.algorithm.get_maximumArea_rectangles_in_a_simple_polygon.version.v1;

/**
 * 数学工具
 */
public class MathUtil {

    public static void main(String[] args) {
        System.out.println(MathUtil.calculateAngleOfVector(-1, -1));
    }

    /**
     * 获取一条直线的斜率
     *
     * @param lx1
     * @param ly1
     * @param lx2
     * @param ly2
     * @return
     */
    public static double getKOfLine(double lx1, double ly1, double lx2, double ly2) {
        double precisionError = 0.000000001;

        double k;
        if (Math.abs(lx2 - lx1) < precisionError) {
            //--if--线段是垂直线
            k = Double.MAX_VALUE;
        } else if (Math.abs(ly2 - ly1) < precisionError) {
            //--if--线段是水平线
            k = 0;
        } else {
            //--if--线段是倾斜的线
            k = (ly2 - ly1) * 1.0 / (lx2 - lx1);
        }
        return k;
    }

    /**
     * 获取直线截距
     *
     * @param x 直线上的点
     * @param y 直线上的点
     * @param k
     * @return
     */
    public static double getBOfLine(double x, double y, double k) {
        double b;

        if (Math.abs(k - Double.MAX_VALUE) < 0.01) {
            b = Double.MAX_VALUE;
        } else if (k == 0) {
            b = y;
        } else {
            b = y - k * x;
        }

        return b;
    }

    /**
     * 计算点到直线的距离
     *
     * @param x
     * @param y
     * @param lx1
     * @param ly1
     * @param lx2
     * @param ly2
     * @return
     */
    public static double calculateDistanceOfPointAndLine(double x, double y, double lx1, double ly1, double lx2, double ly2) {
        double k = MathUtil.getKOfLine(lx1, ly1, lx2, ly2);
        if (k == 0) {
            return Math.abs(y - ly1);
        } else if (k == Double.MAX_VALUE) {
            return Math.abs(x - lx1);
        } else {
            double b = ly2 - k * lx2;
            return Math.abs(k * x - y + b) / Math.sqrt(1 + k * k);
        }
    }

    /**
     * 获取两个点之间的距离
     *
     * @return
     */
    public static double getDistanceOfTwoPoint(double x1, double y1, double x2, double y2) {
        return Math.sqrt(Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2));
    }

    /**
     * 计算向量的模
     *
     * @param x
     * @param y
     * @return
     */
    public static double calculateModulusOfVector(double x, double y) {
        return Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));
    }

    /**
     * 求(x,y)的角度（0,360），从x坐标轴正方向开始计算
     *
     * @param x2
     * @param y2
     * @return
     */
    public static double calculateAngleOfVector(double x2, double y2) {
        double x1 = 1;
        double y1 = 0;
        double radian = Math.acos((x1 * x2 + y1 * y2) / (MathUtil.calculateModulusOfVector(x1, y1) * MathUtil.calculateModulusOfVector(x2, y2)));
        double angle = Math.toDegrees(radian);
        return y2 > 0 ? angle : 360 - angle;
    }

}

【PolygonUtil】

package com.ruoyi.algorithm.get_maximumArea_rectangles_in_a_simple_polygon.version.v1;

import com.ruoyi.algorithm.common.entity.Point;

import java.util.List;

/**
 * @Author dam
 * @create 2023/9/11 17:22
 */
public class PolygonUtil {

    /**
     * 吉林大学的ACM方法：判断点是否处于多边形内部(点处于多边形的边上同样被视为处于多边形内部)
     *
     * @param pointList
     * @param pointA
     * @return
     */
    public static boolean judgeWhetherThePointInPolygon(List<Point> pointList, Point pointA) throws Exception {

        ///首先给点集构造一个包络矩形，判断点是否在包络矩形外部
        double minY = Double.MAX_VALUE;
        double maxY = -Double.MAX_VALUE;
        double minZ = Double.MAX_VALUE;
        double maxZ = -Double.MAX_VALUE;
        for (Point point : pointList) {
            minY = Math.min(minY, point.getY());
            maxY = Math.max(maxY, point.getY());
            minZ = Math.min(minZ, point.getZ());
            maxZ = Math.max(maxZ, point.getZ());
        }
        if (pointA.getY() < minY || pointA.getY() > maxY || pointA.getZ() < minZ || pointA.getZ() > maxZ) {
            return false;
        }

        ///判断点是否在多边形的内部，不包含在多边形的某一条边上
        //构建线1：点A向右延伸的水平射线
        Point line1_start = pointA;
        Point line1_end = pointA.clone();
        line1_end.setY(Double.MAX_VALUE);
        int num = getIntersectNumOfLineSegmentWithPolygon(pointList, line1_start, line1_end);

        boolean isContain = num % 2 != 0;

        ///如果上面识别出来说点不在多边形内部，尝试看看点在不在某一条边上，如果在，则点在多边形内
        if (isContain == false) {
            for (int i = 0; i < pointList.size(); i++) {
                int j = (i + 1) % pointList.size();
                if (PolygonUtil.judgeWhetherThePointInTheLine(pointList.get(i), pointList.get(j), pointA) == true ||
                        PointUtil.judgeWhetherTwoPointsIsSame(pointList.get(i), pointA) ||
                        PointUtil.judgeWhetherTwoPointsIsSame(pointList.get(j), pointA)) {
                    isContain = true;
                    break;
                }
            }
        }
        return isContain;
    }

    /**
     * 判断点 p 是否在线段 line 上
     *
     * @param line_start
     * @param line_end
     * @param p
     * @return
     */
    private static boolean judgeWhetherThePointInTheLine(Point line_start, Point line_end, Point p) {
        double xmulti = xmulti(line_end, p, line_start);
        return ((Math.abs(xmulti - 0) < 0.1 || PolygonUtil.calculateDistanceOfPointAndLine(line_start, line_end, p) < 0.000001) &&
                (((p.getY() - line_start.getY()) * (p.getY() - line_end.getY()) < 0) ||
                        ((p.getZ() - line_start.getZ()) * (p.getZ() - line_end.getZ()) < 0)));
    }

    /**
     * 计算点到直线的距离
     *
     * @param line_start
     * @param line_end
     * @param p
     * @return
     */
    private static double calculateDistanceOfPointAndLine(Point line_start, Point line_end, Point p) {
        return MathUtil.calculateDistanceOfPointAndLine(p.getY(), p.getZ(), line_start.getY(), line_start.getZ(), line_end.getY(), line_end.getZ());
    }

    /**
     * 计算线段和多边形的交点
     *
     * @param pointList
     * @param line1_start
     * @param line1_end
     * @return
     * @throws Exception
     */
    private static int getIntersectNumOfLineSegmentWithPolygon(List<Point> pointList, Point line1_start, Point line1_end) throws Exception {
        //统计射线所穿过多边形中点的数量
        int num = 0;
        //遍历多边形的每条线
        for (int i = 0; i < pointList.size(); i++) {
            //多边形线1（line2）：pointI-pointIPlus1; 多边形线2(line3)：pointIPlus1-pointIPlus2; 多边形线3(line4)：pointIPlus2-pointIPlus3
            Point pointI = pointList.get(i);
            Point pointIPlus1 = pointList.get((i + 1) % pointList.size());
            Point pointIPlus2 = pointList.get((i + 2) % pointList.size());
            Point pointIPlus3 = pointList.get((i + 3) % pointList.size());

            //射线line1和多边形上面的线line2是否相交
            boolean whetherLine1AndLine2IsIntersect = judgeWhetherTwoLineSegmentIsIntersect(line1_start, line1_end, pointI, pointIPlus1);
            //点pointIPlus1是否在射线上
            boolean whetherPointIPlus1InRadial = judgeWhetherThePointInTheLine(line1_start, line1_end, pointIPlus1);
            //点pointIPlus2是否在射线上
            boolean whetherPointIPlus2InRadial = judgeWhetherThePointInTheLine(line1_start, line1_end, pointIPlus2);
            if (whetherLine1AndLine2IsIntersect == true) {
                num++;
                int temp = 0;
            } else if (whetherPointIPlus1InRadial &&
                    (!whetherPointIPlus2InRadial && (xmulti(pointI, pointIPlus1, line1_start) * xmulti(pointIPlus1, pointIPlus2, line1_start) > 0) ||
                            (whetherPointIPlus2InRadial && (xmulti(pointI, pointIPlus2, line1_start) * xmulti(pointIPlus2, pointIPlus3, line1_start) > 0)))) {
                num++;
                int temp = 0;
            }
        }
        return num;
    }

    /**
     * 判断两线段是否相交，当两线段相交且交点不是其中一线段的端点时返回true
     *
     * @param line1_start
     * @param line1_end
     * @param line2_start
     * @param line2_end
     * @return
     */
    public static boolean judgeWhetherTwoLineSegmentIsIntersect(Point line1_start, Point line1_end, Point line2_start, Point line2_end) throws Exception {
        double line1_minY = Math.min(line1_start.getY(), line1_end.getY());
        double line1_maxY = Math.max(line1_start.getY(), line1_end.getY());
        double line1_minZ = Math.min(line1_start.getZ(), line1_end.getZ());
        double line1_maxZ = Math.max(line1_start.getZ(), line1_end.getZ());
        double line2_minY = Math.min(line2_start.getY(), line2_end.getY());
        double line2_maxY = Math.max(line2_start.getY(), line2_end.getY());
        double line2_minZ = Math.min(line2_start.getZ(), line2_end.getZ());
        double line2_maxZ = Math.max(line2_start.getZ(), line2_end.getZ());
        if ((line1_minY > line2_maxY || line2_minY > line1_maxY || line1_minZ > line2_maxZ || line2_minZ > line1_maxZ)) {
            return false;
        } else {
            boolean isTwoLineIntersect = lsinterls(line1_start, line1_end, line2_start, line2_end);
            if (isTwoLineIntersect == false) {
                return false;
            }
            //求交点，用来判断该交点是否为端点
            Point intersectPoint = PolygonUtil.getIntersectPointOfTwoStraightLine(line1_start, line1_end, line2_start, line2_end, -1);
            return ((isTwoLineIntersect) &&
                    (!PointUtil.judgeWhetherTwoPointsIsSame(intersectPoint, line1_start)) &&
                    (!PointUtil.judgeWhetherTwoPointsIsSame(intersectPoint, line1_end)) &&
                    (!PointUtil.judgeWhetherTwoPointsIsSame(intersectPoint, line2_start)) &&
                    (!PointUtil.judgeWhetherTwoPointsIsSame(intersectPoint, line2_end)));
        }
    }

    /**
     * 求两条直线的交点
     *
     * @param line1_start
     * @param line1_end
     * @param line2_start
     * @param line2_end
     * @param polygonIndex
     * @return
     * @throws Exception
     */
    public static Point getIntersectPointOfTwoStraightLine(Point line1_start, Point line1_end, Point line2_start, Point line2_end, int polygonIndex) throws Exception {

        //获取两线段的k和b
        double k1 = PolygonUtil.getKOfLine(line1_start, line1_end);
        double b1 = PolygonUtil.getBOfLine(line1_start, k1);
        double k2 = PolygonUtil.getKOfLine(line2_start, line2_end);
        double b2 = PolygonUtil.getBOfLine(line2_start, k2);

        if (k1 == 0 && k2 == 0) {
            //斜率相同也有可能相交
            if (PointUtil.judgeWhetherTwoPointsIsSame(line1_start, line2_start) || PointUtil.judgeWhetherTwoPointsIsSame(line1_start, line2_end)) {
                return line1_start;
            } else if (PointUtil.judgeWhetherTwoPointsIsSame(line1_end, line2_start) || PointUtil.judgeWhetherTwoPointsIsSame(line1_end, line2_end)) {
                return line1_end;
            } else {
                return null;
            }
        }
        //获取两线段的交点
        double y = 0;
        double z = 0;
        double offSet = 0.000000001;
        if ((Math.abs(k1 - 0) <= offSet) || (Math.abs(k2 - 0) <= offSet) || (Math.abs(k1 - Double.MAX_VALUE) <= offSet) || (Math.abs(k2 - Double.MAX_VALUE) <= offSet)) {
            if (Math.abs(k1 - 0) <= offSet) {
                //line1为水平线时，line2必不可能为水平线，因为已经证明两线相交，平行线必不相交
                z = line1_start.getZ();
                y = (z - b2) / k2;
                if (Math.abs(k2 - Double.MAX_VALUE) < offSet) {
                    y = line2_start.getY();
                } else {
                    y = (z - b2) / k2;
                }
            } else if (Math.abs(k2 - 0) <= offSet) {
                z = line2_start.getZ();
                y = (z - b1) / k1;
                if (Math.abs(k1 - Double.MAX_VALUE) < offSet) {
                    y = line1_start.getY();
                } else {
                    y = (z - b1) / k1;
                }
            } else if (Math.abs(k1 - Double.MAX_VALUE) <= offSet) {
                y = line1_start.getY();
                z = k2 * y + b2;
            } else if (Math.abs(k2 - Double.MAX_VALUE) <= offSet) {
                y = line2_start.getY();
                z = k1 * y + b1;
            } else {
                throw new Exception("判断情况考虑不全面，请仔细考虑");
            }
        } else {
            y = (b2 - b1) / (k1 - k2);
            z = (k2 * b1 - k1 * b2) / (k2 - k1);
        }

        if (Math.abs(z - 290.45) < 1) {
            int temp = 0;
        }
        if (Double.isInfinite(y)) {
            throw new Exception("y为无穷");
        }
        Point point = new Point(0, y, z);
        return point;
    }

    /**
     * 求一条直线的截距
     *
     * @param p 线的一个点
     * @param k 线的斜率
     * @return
     */
    public static double getBOfLine(Point p, double k) {
        return MathUtil.getBOfLine(p.getY(), p.getZ(), k);
    }

    /**
     * 确定两条线段是否相交，端点相交也是相交
     *
     * @param line1_start
     * @param line1_end
     * @param line2_start
     * @param line2_end
     * @return
     */
    public static boolean lsinterls(Point line1_start, Point line1_end, Point line2_start, Point line2_end) {

        double k1 = PolygonUtil.getKOfLine(line1_start, line1_end);
        double k2 = PolygonUtil.getKOfLine(line2_start, line2_end);
        if (Math.abs(k1 - k2) < 0.000001) {
            return false;
        }

        return ((Math.max(line1_start.getY(), line1_end.getY()) >= Math.min(line2_start.getY(), line2_end.getY())) &&
                (Math.max(line2_start.getY(), line2_end.getY()) >= Math.min(line1_start.getY(), line1_end.getY())) &&
                (Math.max(line1_start.getZ(), line1_end.getZ()) >= Math.min(line2_start.getZ(), line2_end.getZ())) &&
                (Math.max(line2_start.getZ(), line2_end.getZ()) >= Math.min(line1_start.getZ(), line1_end.getZ())) &&
                (xmulti(line2_start, line1_end, line1_start) * xmulti(line1_end, line2_end, line1_start) >= 0) &&
                (xmulti(line1_start, line2_end, line2_start) * xmulti(line2_end, line1_end, line2_start) >= 0));
    }

    /**
     * (P1-P0)*(P2-P0)的叉积
     * 若结果为正，则在的顺时针方向；
     * 若结果为零，则共线；
     * 若结果为负，则在的在逆时针方向;
     * 

     * 可以根据这个函数确定两条线段在交点处的转向,
     * 比如确定p0p1和p1p2在p1处是左转还是右转，只要求
     * (p2-p0)*(p1-p0)，若<0则左转，>0则右转，=0则共线
     *
     * @param p1
     * @param p2
     * @param p0
     * @return <0：p2在p1处左拐 =0:直走 >0:p2在p1处右拐
     */
    private static double xmulti(Point p1, Point p2, Point p0) {
        return (
                (p1.getY() - p0.getY()) * (p2.getZ() - p0.getZ())
                        -
                        (p2.getY() - p0.getY()) * (p1.getZ() - p0.getZ())
        );
    }

    /**
     * 求一条直线的斜率
     *
     * @param p1
     * @param p2
     * @return
     */
    public static double getKOfLine(Point p1, Point p2) {
        return MathUtil.getKOfLine(p1.getY(), p1.getZ(), p2.getY(), p2.getZ());
    }

}