【附代码】python采样方法集锦

✅作者简介：在读博士，伪程序媛，人工智能领域学习者，深耕机器学习，交叉学科实践者，周更前沿文章解读，提供科研小工具，分享科研经验，欢迎交流！
个人主页： https://blog.csdn.net/allein_STR?spm=1011.2559.3001.5343
特色专栏：深度学习和WRF，提供人工智能方方面面小姿势，从基础到进阶，教程全面。
联系博主：博文留言+主页左侧推广方式+WeChat code: Allein_STR
本文内容：介绍7种主要的采样方法，并给出python代码示例。

1.随机采样

python代码：

import random

sample = random.sample(population, k)

解读：

random.sample()函数从population中随机选择k个元素作为样本，返回一个列表。其中population可以是一个序列、集合或其他可迭代对象，k为采样数量。

2.等距采样

python代码

import numpy as np

sample = np.linspace(start, stop, num)

解读：

numpy.linspace()函数返回一个等距的样本数组，其中start和stop分别为样本的起始值和结束值，num为采样数量。

3.分层采样

python代码

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y)

解读：

sklearn.model_selection中的train_test_split()函数可以进行分层采样，其中test_size为测试集占比，stratify参数指定分层变量，即按照y的分布进行采样。

4.重采样

python代码

from sklearn.utils import resample

sample = resample(data, n_samples=n)

解读：

sklearn.utils中的resample()函数可以进行重采样，其中data为原始数据，n_samples为采样数量。

以上是常用的Python采样方法及其代码解读。

5.水塘采样(Reservoir sampling)

主要用于解决大数据流中的随机抽样问题，即：当内存有限，数据长度很大，甚至未知，那么如何从中随机选取k个数据，并且要求是等概率

水塘抽样的核心是，只遍历一次，每次都考虑一个问题：当前元素是否被选中，选中后替换之前选中的哪一个元素。

采样过程：集合中总元素个数为n，随机选取k个元素

step1.首先将前k个元素全部选取。

step2.对于第i个元素(i>k)，以概率k/i来决定是否保留该元素，如果保留该元素的话，则随机丢弃掉原有的k个元素中的一个(即原来某个元素被丢掉的概率是1/k)。

结果：每个元素被最终被选取的概率都是k/n。

python代码

假设我们必须从无限大的流中抽取 5 个对象，且每个元素被选中的概率都相等。

import randomdef generator(max):
 number = 1
 while number < max:
 number += 1
 yield number# Create as stream generator
stream = generator(10000)# Doing Reservoir Sampling from the stream
k=5
reservoir = []
for i, element in enumerate(stream):
 if i+1<= k:
 reservoir.append(element)
 else:
 probability = k/(i+1)
 if random.random() < probability:
 # Select item in stream and remove one of the k items already selected
 reservoir[random.choice(range(0,k))] = elementprint(reservoir)
------------------------------------
[1369, 4108, 9986, 828, 5589]

另一种python代码

要随机选择K个元素，那么在遍历到第i个元素时，以k/i的概率选择该元素。

def reservoirSamplingk(arr, k):
    res = arr[:k]
    i = k
    while i < len(arr):
        # 以k/i的概率选取第i个元素，用来等概率的替换之前选中的1个元素
        r = random.randint(0, i)
        if r < k:  # 小于k的概率就是k/i，替换res中第r个已选中的数
            res[r] = arr[i]
        i += 1
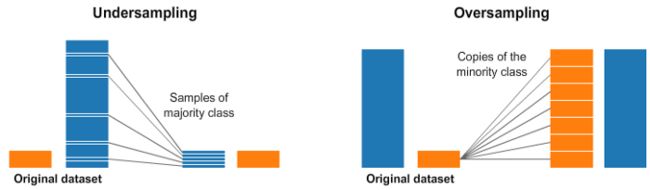
    return res

6.随机欠采样和过采样

我们经常会遇到不平衡的数据集。

一种广泛采用的处理高度不平衡数据集的技术称为重采样。它包括从多数类（欠采样）中删除样本或向少数类（过采样）中添加更多示例。这里只介绍部分算法，其他详细请见博文：

python代码

先创建一些不平衡数据示例。

from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from collections import Counter

# 1.创建类别不平衡的数据集：
# 使用make_classification生成样本数据
X, y = make_classification(n_samples=5000,
                           n_features=2,  # 特征个数 = n_informative() + n_redundant + n_repeated
                           n_informative=2,  # 多信息特征的个数
                           n_redundant=0,  # 冗余信息，informative特征的随机线性组合
                           n_repeated=0,  # 重复信息，随机提取n_informative和n_redundant 特征
                           n_classes=3,  # 分类类别
                           n_clusters_per_class=1,  # 某一个类别是有几个cluster构成的
                           weights=[0.01, 0.05, 0.94],  # 列表类型，权重比
                           random_state=0
                           )

# 2.查看各个标签的样本：
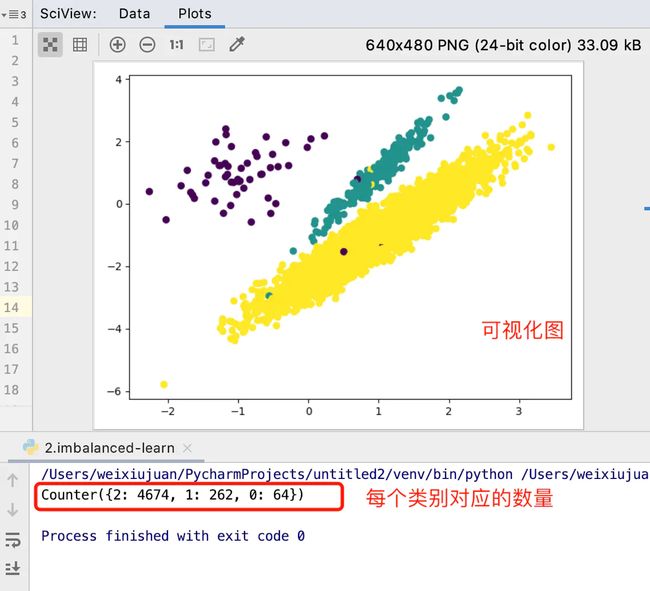
counter = Counter(y)
print(counter) # Counter({2: 4674, 1: 262, 0: 64})

# 3.数据集可视化：
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()

# 4、过采样 
# 4.1 随机过采样
ros = RandomOverSampler(random_state=0)

X_resampled, y_resampled = ros.fit_resample(X, y)
counter_resampled = Counter(y_resampled)
print(counter_resampled)

plt.scatter(X_resampled[:, 0], X_resampled[:, 1], c=y_resampled)
plt.show()

随机过采样的缺点：

（1）对于随机过采样，由于需要对少数类样本进行复制来扩大数据集，造成模型训练复杂度加大。

（2）另一方面也容易造成模型的过拟合问题，因为随机过采样是简单的对初始样本进行复制采样，这就使得学习器学得的规则过于具体化，不利于学习器的泛化性能，造成过拟合问题。

（3）为了解决随机过采样中造成模型过拟合问题，又能保证实现数据集均衡的目的，出现了过采样法代表性的算法SMOTE算法。

7.使用 imbalanced-learn 进行欠采样和过采样

imbalanced-learn（imblearn）是一个用于解决不平衡数据集问题的 python 包，它提供了多种方法来进行欠采样和过采样。

7.1使用 Tomek Links 进行欠采样

如果两个样本点互为最近邻且分属于不同类别，则在它们之间形成Tomek’s link，通过参数sampling_strategy可以选择剔除的样本类别。

python代码

from imblearn.under_sampling import TomekLinks
tl = TomekLinks(sampling_strategy='auto') # 移除多数类样本
# tl = TomekLinks(sampling_strategy='all') # 多数类样本和少数类样本都移除
X_res, y_res = tl.fit_resample(X, y)

7.2使用 SMOTE 进行过采样

Synthetic Minority Oversampling Technique (SMOTE)，通过插值来生成新样本，对于每个少数类样本计算其K个最近的少数类邻居，然后根据采样比率随机选择若干邻居，最后在少数类样本与邻居样本之间进行插值生成新样本。

from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state=42)
X_res, y_res = sm.fit_resample(X, y)

imbLearn 包中还有许多其他方法，可以用于欠采样（Cluster Centroids, NearMiss 等）和过采样（ADASYN 和 bSMOTE）。

---

本篇到这里就结束了。想学习更多Python、人工智能、交叉学科相关知识，点击关注博主，带你从基础到进阶。若有需要提供科研指导、代码支持，资源获取或者付费咨询的伙伴们，可以添加博主个人联系方式！

码字不易，希望大家可以点赞+收藏+关注+评论！

---

参考资料：

https://www.jianshu.com/p/b24c3177ea47

https://zhuanlan.zhihu.com/p/76024846