《动手学深度学习 Pytorch版》 4.4 模型选择、欠拟合和过拟合

4.4.1 训练误差和泛化误差

整节理论，详见书本。

4.4.2 模型选择

整节理论，详见书本。

4.4.3 欠拟合还是过拟合

整节理论，详见书本。

4.4.4 多项回归

import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l

1. 使用以下三阶多项式生成训练数据和测试数据的标签：
   $$y=5+1.2x-3.4\frac{x^2}{2!}+5.6\frac{x^3}{3!}+ϵ$$

   其中噪声项 $ϵ$ 服从均值为 0 且标准差为 0.1 的正态分布，此外将特征值从 $x^i$ 调整为 $\frac{x^i}{i!}$ 可以避免很大的 $i$ 带来过大的指数值从而使梯度或损失值过大。

max_degree = 20  # 多项式的最大阶数
n_train, n_test = 100, 100  # 训练和测试数据集大小
true_w = np.zeros(max_degree)  # 分配大量的空间
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])  # 真实系数

features = np.random.normal(size=(n_train + n_test, 1))  # 生成随机 x
np.random.shuffle(features)  # 打乱
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))  # 分别计算0到20次幂 此处利用了广播机制
for i in range(max_degree):  # 分别除以次数的阶乘，此处使用的 gamma(n)=(n-1)!
    poly_features[:, i] /= math.gamma(i + 1)
labels = np.dot(poly_features, true_w)  # 乘以系数
labels += np.random.normal(scale=0.1, size=labels.shape)  # 加上噪声

# 查看前两个样本
true_w, features, poly_features, labels = [torch.tensor(x, dtype=
    torch.float32) for x in [true_w, features, poly_features, labels]]  # NumPy ndarray转换为tensor

features[:2], poly_features[:2, :], labels[:2]

(tensor([[-0.1243],
         [ 1.3898]]),
 tensor([[ 1.0000e+00, -1.2432e-01,  7.7282e-03, -3.2027e-04,  9.9542e-06,
          -2.4751e-07,  5.1285e-09, -9.1085e-11,  1.4155e-12, -1.9553e-14,
           2.4310e-16, -2.7475e-18,  2.8465e-20, -2.7222e-22,  2.4174e-24,
          -2.0036e-26,  1.5568e-28, -1.1385e-30,  7.8638e-33, -5.1456e-35],
         [ 1.0000e+00,  1.3898e+00,  9.6571e-01,  4.4737e-01,  1.5543e-01,
           4.3203e-02,  1.0007e-02,  1.9867e-03,  3.4513e-04,  5.3294e-05,
           7.4066e-06,  9.3576e-07,  1.0837e-07,  1.1586e-08,  1.1501e-09,
           1.0656e-10,  9.2554e-12,  7.5663e-13,  5.8418e-14,  4.2730e-15]]),
 tensor([4.9927, 5.8647]))

2. 对模型进行训练和测试

   分别是实现损失函数和训练函数

def evaluate_loss(net, data_iter, loss):  #@save
    """评估给定数据集上模型的损失"""
    metric = d2l.Accumulator(2)  # 损失的总和,样本数量
    for X, y in data_iter:
        out = net(X)
        y = y.reshape(out.shape)
        l = loss(out, y)
        metric.add(l.sum(), l.numel())
    return metric[0] / metric[1]

def train(train_features, test_features, train_labels, test_labels,
          num_epochs=400):
    loss = nn.MSELoss(reduction='none')
    input_shape = train_features.shape[-1]
    # 不设置偏置，因为我们已经在多项式中实现了它
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
    batch_size = min(10, train_labels.shape[0])
    train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
                                batch_size)
    test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
                               batch_size, is_train=False)
    trainer = torch.optim.SGD(net.parameters(), lr=0.01)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
                            xlim=[1, num_epochs], ylim=[1e-3, 1e2],
                            legend=['train', 'test'])
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
                                     evaluate_loss(net, test_iter, loss)))
    print('weight:', net[0].weight.data.numpy())

3. 三阶多项式函数拟合（正常）

# 从多项式特征中选择前 4 个维度，即 1, x, x^2/2!, x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
      labels[:n_train], labels[n_train:])

weight: [[ 4.9966974  1.2050456 -3.393899   5.60854  ]]

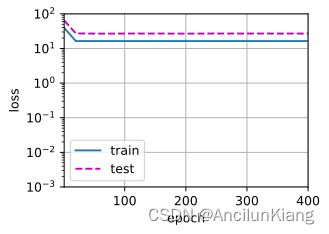
4. 线性函数拟合（欠拟合）

# 从多项式特征中选择前 2 个维度，即 1 和 x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
      labels[:n_train], labels[n_train:])

weight: [[3.040382  5.0033937]]

5. 高阶多项式函数拟合（过拟合）

# 从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:, :],
      labels[:n_train], labels[n_train:], num_epochs=1500)

weight: [[ 5.019969    1.2532085  -3.4963152   5.322493    0.14574984  0.7863229
   0.42101192  0.1502814   0.31017718 -0.07281512 -0.0655788   0.14933251
  -0.12562694 -0.18436337 -0.20441814 -0.2126619   0.157519   -0.16071859
   0.02987491 -0.14533804]]

ps：好怪，随机出来的数据有时候不但不过拟合，甚至测试损失比训练损失都低。

练习

（1）多项式回归问题可以准确的解出吗？（提示：使用线性代数。）

令 $\hat{\mathbf{y}}=\mathbf{XW}$，其中 $\mathbf{X}=1,\mathbf{x},\frac{{\mathbf{x}}^2}{2!},\frac{{\mathbf{x}}^3}{3!}$

此问题为求 $\mathbf{W}$ 的解析解，使得 $L(\mathbf{X},\mathbf{W})=\frac{1}{2}||\mathbf{y}-\hat{\mathbf{y}}|{|}_2$ 最小

令损失式对 $\mathbf{W}$ 的偏导为 0 即可。

具体求解过程可见 3.1.练习（2）

可得：

$$\mathbf{W}=({\mathbf{X}}^T\mathbf{X}{)}^{-1}{X}^T\mathbf{y}$$

---

（2）考虑多项式的模型选择。

a. 绘制训练损失与模型复杂度（多项式的阶数）的关系图。从关系图中能观察到什么？需要多少阶的多项式才能将训练损失减小到 0？

b. 在这种情况下绘制测试的损失图。

c. 生成同样的图，作为数据量函数。

不会…

---

（3）如果不对多项式特征 $x^i$ 进行标准化 $(1/i!)$，会出现什么问题？能用其他方法解决这个问题吗？

如上所述，将特征值从 $x^i$ 调整为 $\frac{x^i}{i!}$ 是为了避免很大的 $i$ 带来过大的指数值从而使梯度或损失值过大。

取对数之类的应该也可以。

---

（4）泛化误差可能为零吗？

应该是不可能的，毕竟还有噪声项，不可能完全拟合。