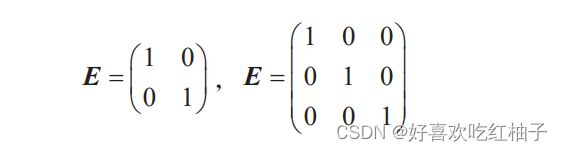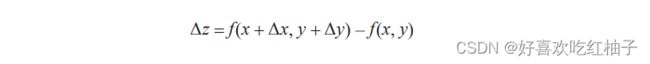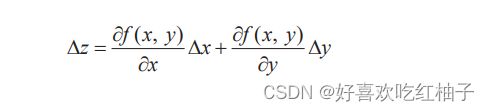深度学习小白理论入门(一)之必备数学基础(自用笔记,方便快速查阅)
笔记参考和图片来源:《深度学习的数学》
深度学习的数学 (ituring.com.cn)
目录
一、正态分布
二、递推关系式
三、∑符号
四、向量
4.1 向量内积
4.2 柯西 - 施瓦茨不等式
4.3 内积的坐标表示
4.4 向量的一般化
五、矩阵
5.1 单位矩阵
5.2 Hadamard 乘积
六、导数(单变量函数)
6.1 导数定义
6.2 分数函数的导数和Sigmoid函数的导数
6.3 如何求得最小值
七、偏导数(多变量函数)
7.1 多变量函数
7.2 偏导数
7.3 如何求得最小值
7.4 拉格朗日数乘法
八、链式法则
8.1 复合函数
8.2 单变量的复合函数求导公式
8.3 多变量的复合函数求导公式
九、变量函数的近似公式
9.1 单变量函数的近似公式
9.2 多变量函数的近似公式
9.3 近似公式的向量表示
十、梯度下降法
10.1 二变量函数的梯度下降法的基本式
推导过程
10.2 梯度
10.3 三变量函数的梯度下降法的基本式
10.4 哈密顿算子
10.5 η 的含义:学习率
十一、最优化问题和回归分析
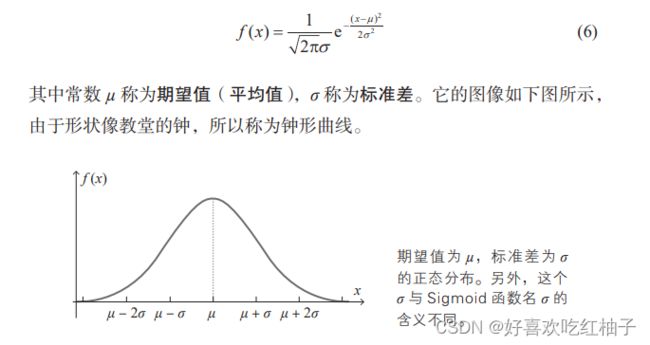
一、正态分布
设定权重和偏置的初始值时使用服从正态分布的随机数一般可以取得好的结果。
二、递推关系式
计算机擅长关系式的计算。
例如,我们来看一下阶乘的计算。自然数 n 的阶乘是从 1 到 n 的整数的 乘积,用符号 n! 表示。
n! = 1×2×3×…×n
在多数情况下,人们是根据上面的式子来计算 n! 的,而计算机则通常用 以下递推关系式来计算。
a1 = 1,an + 1 = (n + 1)an
误差反向传播法就是通过计算机所擅长的这一计算方法来进行神经网络的计算的。
三、∑符号
四、向量
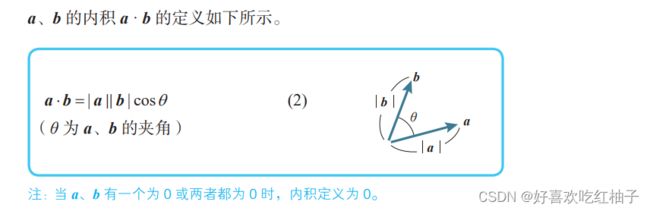
4.1 向量内积
a⋅b = | a | | b |cosθ (θ 为 a、b 的夹角)
4.2 柯西 - 施瓦茨不等式
性质1可以应用于梯度下降法(梯度的反方向下降最快)。
4.3 内积的坐标表示
二维空间:
三维空间:
4.4 向量的一般化
在神经网络的计算过程中,向量的观点是十分有益的。
神经单元有多个输入 x1, x2, …, xn 时,可以将它们整理为如下的加权输入。
五、矩阵
5.1 单位矩阵
单位矩阵,它是对角线上的元素1、其他元素为 0 的方阵,通常用 E 表示。
例如,2 行 2 列、3 行 3 列的单位矩阵E(称为 2 阶单位矩阵、3 阶单位矩阵)分别如下表示。
单位矩阵是具有与 1 相同性质的矩阵,单位矩阵 E与任意矩阵A的乘积都满足以下交换律。
AE = EA = A
5.2 Hadamard 乘积
六、导数(单变量函数)
6.1 导数定义
6.2 分数函数的导数和Sigmoid函数的导数
分数函数的导数:
Sigmoid函数的导数:
6.3 如何求得最小值
当函数f(x)在x = a处取得最小值时,f'(a) = 0。
七、偏导数(多变量函数)
7.1 多变量函数
有两个以上的自变量的函数称为多变量函数。
f(x1, x2, …, xn) :有 n 个自变量 x1, x2, …, xn 的函数。
神经网络的函数变量即有成千上万个。
7.2 偏导数
关于某个特定变量的导数就称为偏导数(partial derivative)。
7.3 如何求得最小值
7.4 拉格朗日数乘法
八、链式法则
8.1 复合函数
已知函数 y = f(u),当 u 表示为 u = g(x) 时,y 作为 x 的函数可以表示 为形如 y = f(g(x)) 的嵌套结构(u 和 x 表示多变量)。这时,嵌套结构的函 数 f(g(x)) 称为 f(u) 和 g(x) 的复合函数。
在神经网络中的函数也是一个典型的复合函数。
8.2 单变量的复合函数求导公式
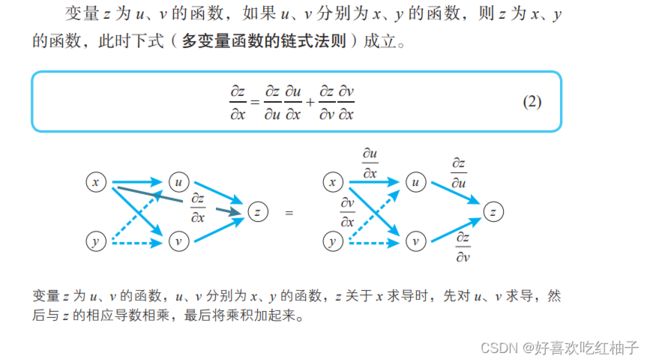
8.3 多变量的复合函数求导公式
z = f(u,v), 对x变量求偏导数:
对y变量求偏导数:
C = f(u,v,w),对u求偏导数:(对v和w同理)
九、变量函数的近似公式
梯度下降法是确定神经网络的一种代表性的方法。在应用梯度下降法时,需要用到多变量函数的近似公式。
9.1 单变量函数的近似公式
9.2 多变量函数的近似公式
对公式进行简化,把当 x、y 依次变化 ∆x、∆y 时函数 z = f(x, y) 的变化使用字母z表示:
得到简化版的近似公式如下所示,同理,三变量的函数近似公式也可如此表示。
9.3 近似公式的向量表示
近似公式可以表示为如下两个向量的内积 ∇ z⋅∆ x 的形式。
十、梯度下降法
梯度下降法是寻找函数最小值的最常用方法,即利用负梯度方向来决定每次迭代的新的搜索方向,使得每次迭代能使待优化的目标函数逐步减小。
10.1 二变量函数的梯度下降法的基本式
推导过程
当 x 改变 ∆x,y 改变 ∆y 时,函数 f (x, y) 的变化 ∆z 为:
上述公式可以表示为两个向量a和b的内积形式。
已知当 b 的方向与 a 相反时, 内积 a · b 取最小值。即当向量 b 满足 b= - ka (k为正的常数),使得内积 a · b 取最小值。
也就是说,当a和b两个向量的方向恰好相反时,可以使得 ∆z 达到最小(即减小得最快)
由此可以得出二变量函数的梯度下降法的基本式。
从点 (x, y) 向点 (x + ∆x, y + ∆y) 移动时, 当满足:
函数 z = f (x, y) 减小得最快。
10.2 梯度
梯度是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
10.3 三变量函数的梯度下降法的基本式
二变量函数的梯度下降法的基本式可以很容易地推广到三个变量以上的情形。当函数 f 由 n 个自变量 x1, x2, …, xn 构成时,可以推广出三变量的基本式。
10.4 哈密顿算子
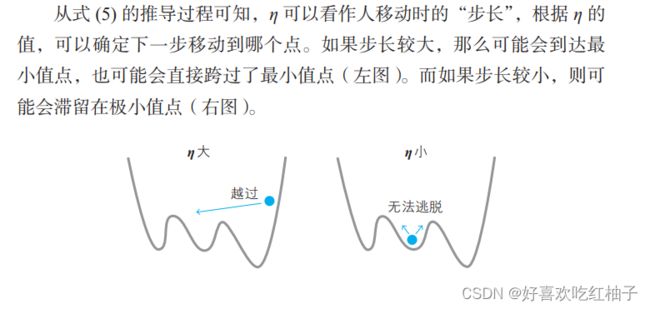
10.5 η 的含义:学习率
在神经网络的世界中,η 称为学习率。它的确定方法没有明确的标准,只能通过反复试验来寻找恰当的值。
十一、最优化问题和回归分析
在最优化方面,误差总和可以称为“误差函数”“损失函数”“代价函数”等。利用平方误差的总和进行最优化的方法称为最小二乘法。