MAML在隐式神经表示中的应用
论文
- Learned Initializations for Optimizing Coordinate-Based Neural Representations
-
- Abstract
- 1. Introduction
- 2. Related Work
- 3. Overview ⭐
- 4. Results
- 5. Conclusion
- 6. Acknowledgements
- A. Implementation details
- Implicit Neural Representations for Image Compression
-
- Abstract
- 1. Introduction
- 2. Related Work
- 3. Method
- 4 Experiments
- 5 Conclusion
- 6 Acknowledgements
- 7. Supplementary Material
- MetaSDF: Meta-learning Signed Distance Functions
-
- Abstract
- 1 Introduction
- 2 Related Work
- 3 Meta-learning Signed Distance Functions
- 4 Analysis
- COIN++: Neural Compression Across Modalities
-
- Abstract
- 1 Introduction
- 2 Method
- 2.1 Storing modulations
- 2.2 Meta-learning modulations
- 2.3 Patches, quantization and entropy coding for modulations
- 3 Related Work
- 4 Experiments
- 5 Conclusion, limitations and future work
Learned Initializations for Optimizing Coordinate-Based Neural Representations
Abstract
基于坐标的神经表示作为一种离散的、基于数组的复杂低维信号表示的替代方法,已经显示出了巨大的前景。然而,通过随机初始化每个新信号的权重来优化基于坐标的网络是低效的。我们建议应用标准的元学习算法,根据所表示的潜在信号类别来学习这些全连接网络的初始权重参数。只需要对实现进行很小的更改,就可以用这些学习到的初始权重在优化过程中实现更快的收敛,并且可以作为正在建模的信号类的强先验,从而在只有部分观测到的给定信号可用时产生更好的泛化。我们在各种任务中探索这些好处,包括表示 2D 图像,重建 CT 扫描,以及从 2D 图像观察中恢复 3D 形状和场景。
1. Introduction
最近的工作已经证明了使用深度全连接神经网络 (通常称为多层感知器或 MLPs) 表示复杂低维信号的潜力。给定信号的基于坐标的神经表示 f θ f_\theta fθ 是一个 MLP (具有权重 θ θ θ),它被优化为从输入坐标 x x x 映射到该坐标处的信号值。例如, f θ f_θ fθ 可以从 2D 像素坐标映射到 RGB 颜色值来编码图像。与存储为离散采样值数组的信号不同,基于坐标的神经表示是连续的,不受限于具有固定的空间分辨率。与 3D 体素网格相比,这一事实最近被用于设计不需要立方体存储复杂性的 3D 形状 (通常占据 3D 空间的一小部分 2D 子集) 的表示[23,25,28,35]。
【图1. 基于坐标的 MLP 以坐标作为输入,并在该位置输出一个值。例如,网络可以接收一个像素坐标 ( x , y ) (x,y) (x,y) 发出 ( R , G , B ) (R,G,B) (R,G,B) 该像素的颜色作为输出,从而表示二维图像。网络权重 θ θ θ 通常通过梯度下降进行优化,以产生所需的图像。然而,寻找好的参数在计算上可能是昂贵的,并且必须为每个新目标重复完整的优化过程。我们建议使用元学习来找到允许更快收敛和更好泛化的初始网络权值 θ 0 ∗ θ_0^* θ0∗。】
然而,这些神经表征的一个限制是,计算重现给定信号的网络权重 θ θ θ 通常需要通过运行多个梯度下降步骤来解决优化问题。这可能需要几秒钟 (当编码小图像时) 和几个小时 (当解决反问题以恢复高分辨率的辐射场时,如在 NeRF [25]中)。解决这一问题的常见方法包括将潜在向量连接到输入坐标,并监督单个神经网络来表示一整类信号[23,28],或者训练超网络从信号观测 (或潜在代码) 映射到 MLP 权重[34,35]。然而,这些策略中的每一种都被限制为仅表示其学习潜在空间内的信号,潜在地限制了其表达先前未见过的目标信号的能力。
最近的研究[33]表明,基于优化的元学习可以显著减少优化神经表示以编码二维和三维形状的符号距离域的新信号所需的梯度下降步骤的数量。在这项工作中,我们建议学习跨各种潜在信号类型 (如图像、体积数据和3D场景) 的神经表示的权重初始化。我们表明,与标准随机初始化相比,使用固定的学习值作为初始网络权重的强先验,可以在优化过程中更快地收敛,并且在只有部分目标信号可用时更好地泛化。在使用神经表示从图像中进行 3D 重建的背景下,专门针对特定 ShapeNet [3]类的学习初始化允许网络在优化过程中从单个图像中恢复 3D 形状,而标准随机初始化网络除非提供多个输入视图,否则会失败。给定一个元训练集,包括从固定的底层类中采样的不同信号的观察值,我们的设置应用基于优化的元学习算法 (MAML [7]或 Reptile [26]),以产生更适合表示特定信号类的初始权重 (例如,来自 CelebA [21]的人脸图像或来自 ShapeNet [3]的 3D 椅子)。
我们的方法最大的优点是简单。给定用于神经表示的测试时优化的现有框架,使用 MAML 或 Reptile 更新步骤实现外部循环只需要额外的几行代码和训练示例的数据集。一旦元学习阶段完成,学习到的初始权重就可以存储起来,然后在需要编码新信号时重新加载,代替标准网络初始化。这个微小的实现变化可以显著地改变优化期间的网络行为。
2. Related Work
Neural Representations. 神经表征最近作为三维形状的紧凑表征而变得突出。这些方法将形状表示为定义为 MLP 网络水平集的隐式曲面,并支持从不完整的 3D 点云数据或深度扫描中重建完整物体[4,5,10,11,15,23,24,28]。后来的工作将这一想法与各种可微渲染公式结合起来,仅使用 2D 图像观测就可以恢复 3D 形状的神经表征[19,20,25,27,35,38]。
基于坐标的神经网络也被用于表示其他低维信号,如二维图像,其中这种网络 (通过遗传算法训练时) 被称为构成模式生成网络[36]。最近的研究表明,由于频谱偏置[29],标准的 ReLU MLPs 无法在这些复杂的低维信号中充分表示细节,并通过用正弦函数代替 ReLU 激活[34]或将输入坐标提升到傅里叶特征空间[37]来解决这一问题。我们的工作利用了这些观察结果,并提出了一种技术,使基于坐标的 MLP 能够从拟合类别内许多信号的过程中学习,从而可以使用更少的步骤和更少的观察值快速优化以拟合任何新信号。
Meta-learning. 元学习通常解决少量学习的问题,即使用给定任务的一些示例 (包括训练和测试数据) 来学习一种算法,该算法可以在相同任务的新的、以前未见过的实例上获得更好的性能。来自计算机视觉的一个典型例子是少量图像分类,其中网络必须学习在测试时仅基于每个类的少量标记实例来区分新类。
与这项工作最相关的是基于优化的元学习算法,如模型不可知元学习 (Model-Agnostic Meta Learning, MAML) [7]和 Reptile [26],以及各种扩展[1,6,8,18,30]。给定用于执行任务的网络架构,这些方法使用基于梯度的学习的外部循环来找到一个权重初始化,该权重初始化允许网络在测试时更有效地优化底层任务的新实例。这些方法假设在测试时使用标准的基于梯度的优化方法,如随机梯度下降或Adam [17],使它们易于在现有实现的基础上分层,而不是像 Ravi 等[31]这样更复杂的方法,后者训练“元学习者” LSTM 网络为底层任务执行梯度更新。Hospedales 等人[13]的调查论文对元学习算法进行了详尽的回顾。
MetaSDF [33]专门将这种学习权重初始化的想法应用于拟合神经表征以表示带符号距离域的任务,并表明该策略比 DeepSDF [28]等标准方法实现了更快的收敛。我们的工作将元学习应用于更广泛的潜在信号类型的神经表示,并进一步探索使用初始权重设置作为先验的能力。
3. Overview ⭐
我们定义一个有限信号 T T T 作为一个从有界集合 C ∈ R d C\in\mathbb{R}^d C∈Rd 到 R n \mathbb{R}^n Rn 映射的函数,其中我们把元素 x ∈ C x\in C x∈C 称为 d d d 维坐标。示例包括图像 (从 2D 像素坐标映射到 3D 颜色值) 或 3D 形状的体积表示 (从 3D 位置映射到 4D 颜色和密度元组) 。对于 T T T,基于坐标的神经表示 f θ f_θ fθ 是一个具有 d d d 个输入通道和 n n n 个输出通道的全连接神经网络,其权值 θ θ θ 经过优化,使得对于 x ∈ C x\in C x∈C 中的所有坐标, f θ f_θ fθ 尽可能地与 T T T 匹配。
如果信号 T T T 的直接点观测 { ( x i , T ( x i ) } i \{(x_i,T(x_i)\}_i {(xi,T(xi)}i 是可用的,则可以使用简单的 L2 损失通过梯度下降来监督 f θ f_θ fθ:
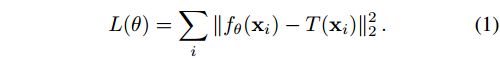
设 θ 0 θ_0 θ0 为采取任何梯度步骤前的初始网络权值,设 θ i θ_i θi 为优化 i i i 步后的权值。基本梯度下降应用规则:
![]()
而更复杂的优化器,如 Adam[17],会随着时间的推移跟踪梯度矩,从而重定向优化轨迹。给定 m m m 个优化步骤的固定预算,不同的初始权值 θ 0 θ_0 θ0 将导致不同的最终权值 θ m θ_m θm 和信号逼近误差 L ( θ m ) L(θ_m) L(θm)。当强调 θ m θ_m θm 对初始权重和特定信号的函数依赖性时,我们将写成 θ m ( θ 0 , T ) θ_m(θ_0,T) θm(θ0,T)。
通常情况下,只能通过某种前向测量模型 M ( T , p ) M(T,p) M(T,p) 对 T T T 进行间接观测。例如,如果 T T T 是一个 3D 物体, M ( T , p ) M(T,p) M(T,p) 可以是从相机姿势 p p p 捕获的物体的 2D 图像。在这种情况下,从观察结果 { p i , M ( T , p i ) } i \{p_i,M(T,p_i)\}_i {pi,M(T,pi)}i 中恢复 T T T 的神经表示需要通过对包含正演模型 M M M 的损失采取梯度步骤来解决一个逆问题:
通常情况下,只有对 T T T 的间接观测是可用的,通过一些前向测量模型 M ( T , P ) M(T,P) M(T,P). 例如,如果 T T T 是一个 3D 物体,则 M ( T , p ) M(T,p) M(T,p) 可以是从相机姿势 p p p 捕获的物体的二维图像。在这种情况下,从 { p i , M ( T , p i ) } i \{p_i,M(T,p_i)\}_i {pi,M(T,pi)}i 需要通过对包含正演模型 M M M 的损失采取梯度步来解决一个逆问题:
![]()
如果 M M M 丢弃了太多关于 T T T 的信息,或者提供的观测集太小,则得到的网络 f θ f_θ fθ 可能与 T T T 不太匹配。例如,如果没有对物体形状的先验知识,就不可能从单个 2D 视图中准确地恢复 3D 物体。
3.1. Optimizing initial weights
我们假设有一个来自特定分布 T \mathcal{T} T 的信号 T T T 的观测数据集 (例如,2D 人脸图像或 3D 椅子),我们的目标是找到初始权重 θ 0 ∗ θ_0^* θ0∗,当优化网络 f θ f_θ fθ 以表示来自相同分布的新的,以前未见过的信号时,它将导致最低可能的最终损失 L ( θ m ) L(θ_m) L(θm):
![]()
尝试学习网络的初始权重作为跨任务分布的梯度下降的良好起点的问题由各种基于优化的元学习算法解决,例如 MAML [7]和 Reptile [26]。
MAML[7]. 给定任务 T T T,计算权值 θ m ( θ 0 , T ) θ_m(θ_0,T) θm(θ0,T) 需要进行 m m m 个优化步骤,这些步骤统称为内循环。MAML 在这个内循环周围包装了一个元学习的外循环,以便学习初始权重 θ 0 θ_0 θ0。每个外环从 T T T 中采样信号 T j T_j Tj,并应用更新规则:
![]()
元学习步长为 β β β。这个更新规则将梯度下降应用于权重 θ m ( θ 0 j , T j ) θ_m(θ_0^j,T_j) θm(θ0j,Tj) 由内循环优化得到。
Reptile[26]. Reptile 使用与 MAML 相同的元学习设置,但应用了一个更简单的更新规则,不需要计算二阶梯度:
![]()
该规则将先前的权值初始化 θ 0 j θ_0^j θ0j 转向任务优化权值 θ m ( θ 0 J , T j ) θ_m(θ_0^J,T_j) θm(θ0J,Tj)。
3.2. Experimental setup
前面描述的元学习算法在概念上很简单,当在测试时间 (元学习完成后) 给出一个新信号进行编码时,不需要改变基于坐标的神经表示的架构或优化过程。这些算法只产生一组初始网络权值 θ 0 ∗ θ_0^* θ0∗,然后用作梯度下降的起点。新信号的测试时间优化并不局限于与元学习期间内循环中使用的相同步数 m m m;实际上,在测试时,我们经常观察到,与元学习算法的内部循环相比,优化更多迭代所带来的好处。
给定固定数量的内部循环步骤 m m m, MAML 通常能够产生比 Reptile 更好的初始化,但是 Reptile 可以展开更多的内部循环步骤,因为它比 MAML 更少占用内存。对于某些任务,MAML 有限的内循环步数意味着它只能观察到目标信号观测值的一小部分。在这些情况下,我们使用 Reptile 来最大化内部循环过程中看到的不同观察的数量。实验中我们发现,对于更复杂的任务,展开更多的步骤是有益的。
我们的每个实验都包括两个阶段:
- Meta-learning,其中我们使用 MAML 或 Reptile 结合示例任务的训练数据集 (不同信号实例的观察)来优化该类信号的初始网络权重,以及
- Test-time optimization,其中我们使用标准的基于梯度的优化来拟合网络的权重,以观察来自同一类的先前未见过的信号。
我们的目标是回答以下问题:在测试时间优化期间,不同的初始网络权重设置如何影响神经表示适应新信号的能力?
4. Results
我们介绍了二维图像回归、二维计算机断层扫描 (CT) 重建、三维物体重建和三维场景重建的结果。对于每个任务,我们展示了使用优化的元学习初始权重来重建特定类别的信号的好处。
对于 2D 图像回归,元学习权重初始化可以在测试时间优化期间更快地收敛和更好地性能。对于 CT 重建,在测试时间优化过程中,可以通过更少的监督视图获得更好的重建质量。对于图像的 3D 形状重建,它允许在测试时间更快的收敛,并使单视图重建成为可能。
4.1. Tasks
这里我们为每个任务提供基本设置。请参阅附录了解完整的实施细节。
Image regression. 基于坐标的神经表示的一个典型例子是 M L P MLP MLP,它通过获取 2D 像素坐标并输出 RGB 颜色值来优化表示 2D 图像[34,37]。我们考虑了四种不同的分布 T \mathcal{T} T:人脸图像(CelebA[21])、自然图像(Imagenette[14])、文本图像(text)和简单曲线的二维符号距离场(SDF)。每个类别包含大约一万个例子。给定采样图像 T ∼ T T\sim\mathcal{T} T∼T,我们提供所有 178×178 像素作为内环中优化网络权重 θ θ θ 的观测值。由于此任务不受内存约束,我们使用 M A M L MAML MAML 对 2 个展开梯度步骤的权重进行元学习 (分别针对每个类别 T \mathcal{T} T)。在每个内环步骤中,整个图像被重建并用于计算损失。对于 MLP f θ f_θ fθ,我们使用 5 层,每层 256 通道和正弦函数非线性,如 SIREN[35]。
4.2. Baselines
除了标准随机初始化网络 (Glorot et al .[12]),我们在几个实验设置中比较了各种其他初始化方案:
- Mean: 我们从头开始优化网络,使其输出与当前类 T \mathcal{T} T 的平均信号 E T ∼ T [ T ] E_{T\sim\mathcal{T}}[T] ET∼T[T] 相匹配。
- Matched: 我们从头开始优化网络,使其输出与使用当前类 T \mathcal{T} T 的元学习初始化的网络输出相匹配。
- Shuffed: 我们对当前类 T \mathcal{T} T 的元学习初始化 θ 0 ∗ θ_0^* θ0∗ 的权值(在每个网络层内)进行随机排列。
Mean 基线和 Matched 基线都表明了在信号空间和权重空间中拥有良好初始化的区别——尽管 Mean 和 Matched 基线被初始化,这样随机采样信号的损失就会很低,但对于梯度下降来说,它们是比实际的元学习初始权重更糟糕的起点。shuffed 基线表明,匹配元学习初始权重的统计分布不足以获得更好的收敛或泛化。我们发现,使用 Adam [17]优化器对所有基线初始化效果最好,但标准随机梯度下降对元学习初始化效果最好(我们为每个任务选择最佳优化器和超参数,并使用一个保留验证集初始化,详见补充)。
4.3. Faster convergence
Image regression. 在 图2 中,我们可视化了各种初始权重设置的网络输出,显示了测试时间优化的 0、1 和 2 个梯度步骤后的输出图像。优化元学习的初始权重以表示人脸图像 (CelebA[21])。当使用学习到的初始权值 θ 0 ∗ θ_0^* θ0∗ (Meta) 时,在第一步之后,目标图像已经清晰可见。相比之下,基线初始化方法需要多一个数量级的迭代才能以相同的精度表示目标图像 (见 表1)。Mean、Matched 和 Shuffled 基线的性能优于完全随机的 Standard 初始化,但仍然需要 10 倍以上的迭代才能达到与元初始化网络相同的质量。特别是,这表明匹配图像空间输出和元学习权重的统计分布都不足以实现类似的加速。

【图2. 更快的收敛:优化网络以表示来自不同初始权重设置的 2D 图像的示例。元学习初始化 (Meta) 是专门针对人脸图像的,但仍然有助于加速对其他自然图像的收敛 (右)。非元初始化网络需要10 到 20 倍的迭代才能达到与元初始化网络相同的质量,只需 2 个梯度步骤 (见 表1)。】
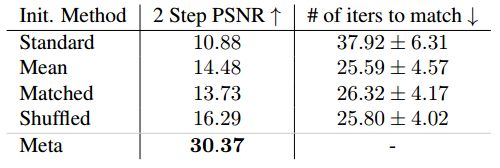
【表1. 使用 CelebA 数据集的图像回归任务不同初始化方法的比较。我们报告了经过两步测试时间优化后的重构 PSNR。元学习初始化 (Meta) 明显优于所有其他初始化。我们还报告了在两步之后匹配 Meta 精度所需的平均迭代次数。】
4.4. Generalizing from partial observations
Image regression within a category. 我们跨多个数据集执行元学习实验,以确定优化的权重初始化作为类特定先验的程度。我们比较了在四种不同的图像数据集 (CelebA、Imagenette、Text 和 SDF) 上训练的初始化。表2 给出了一个混淆矩阵,表明优化网络初始化实际上会产生一个依赖于数据集的先验,每个学习到的初始化都最好地推广到它所训练的相同数据集分布。
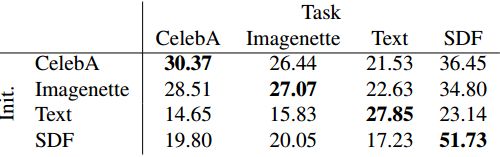
【表2. 四种不同学习初始化图像回归的 PSNR 比较。每行对应于不同底层图像数据集上的初始化元学习。这些列表示在测试期间从哪些数据集图像进行采样。每个任务的最佳初始化是对从相同数据集绘制的训练图像进行专门优化的初始化。我们观察到初始化在更相似的数据集 (CelebA 和 Imagenette,都是自然图像) 之间转移得更好,而在不太相似的数据集之间转移得很差 (文本图像的频谱与其他类别的频谱不同)。】
5. Conclusion
我们的研究结果表明,只需修改基于坐标的神经表示的初始权值,就可以在不改变底层架构或测试时间优化过程的情况下,引导网络沿着更好的优化轨迹运行。这些元学习的初始权重可以导致更快的收敛,或者作为表示给定分布的信号的强先验。这部分改善了神经表示的主要缺点(为每个新信号单独优化网络),而不限制它们的表示能力。
还有许多其他方向需要探索,例如应用更复杂的元学习算法或更精确地表征这些网络的权重空间的几何形状。我们当前方法的一个限制是,它需要来自目标分布的样本信号的相当大的数据集,以便获得有益的初始权重。另一个缺点是我们的方法仍然需要一些测试时间优化。
随着神经表示用例的数量持续快速增长,我们相信这项工作在理解其初始权重和优化行为的重要性方面迈出了重要的一步。
6. Acknowledgements
MT 由 NSF 奖学金和伯克利深度驱动基金资助。BM 是由谷歌通过 BAIR 公共项目资助的。谷歌大学关系提供了 GCP 计算学分的慷慨捐赠。我们感谢 NVIDIA 的任瑞超捐赠 GPU 硬件。
A. Implementation details
我们发现修改这些基于坐标的网络的权值初始化极大地改变了它们在测试时间优化时的收敛行为。因此,我们为每个实验的每个部分 (使用 hold -out 验证集) 调整了优化方法和超参数,以便提供尽可能公平的比较,并且不会使结果与非元学习初始化产生偏差。例如,我们经常发现,在使用元学习初始化进行测试时优化时,SGD 的表现优于 Adam,但是 Adam 明显优于使用标准随机初始化的 SGD。
所有实验均在 JAX 中实现[2]。每个实验都在单个 NVIDIA V100、2080 Ti 或 3080 Ti 上进行训练。在使用 Adam 优化器[17]的所有情况下,我们保持 β 1 = 0.9 β_1=0.9 β1=0.9, β 2 = 0.999 β_2=0.999 β2=0.999, ϵ = 1 0 − 8 ϵ=10^{−8} ϵ=10−8 的标准参数选择。
A.1. Image regression
对于这个任务,我们使用了 SIREN [34]架构( w 0 w_0 w0=200),共 5 层,每层 256 个通道。对于随机初始化的标准基线,我们使用 SIREN 论文中提出的具体初始化程序。MAML [7]训练了 150K 次迭代。每次迭代的外部批处理大小为 3 个目标图像。内部批处理包含目标图像的所有像素。外循环使用 Adam 优化器,学习率为 10−5。内环进行两步梯度下降,学习率为 10−2。
我们还使用 Reptile 元学习另一种初始化[26]。我们使用与 MAML 相同的学习率,但外部批处理大小为 10 个目标图像。我们在 表6 中报告了 Reptile 重建的精度。我们注意到 Reptile 也优于非元学习的权重。
在测试时间优化中,我们从 MAML 初始权重开始,使用学习率为 10−2 的梯度下降。对于基线方法(Standard, Mean, Matched, Shuffled),我们使用学习率为 10−4 的 Adam,其表现明显优于梯度下降。
Implicit Neural Representations for Image Compression
Abstract
隐式神经表示(INRs)作为一种新颖有效的数据类型表示而受到关注。近年来,已有研究将红外光谱应用于图像压缩。这种压缩算法很有希望成为任何基于坐标的数据模式的通用方法。然而,为了实现这一承诺,当前基于 INR 的压缩算法需要大幅提高其率失真性能。这项工作在这个问题上取得了进展。首先,我们提出了基于 INR 压缩的元学习初始化,以提高率失真性能。作为一个副作用,它也导致更快的收敛速度。其次,与之前基于 INR 的压缩工作相比,我们对网络架构进行了简单而高效的更改。也就是说,我们将 SIREN 网络与位置编码相结合,提高了速率失真性能。我们对使用 INR 进行源压缩的贡献大大优于先前的工作。我们的基于 INR 的压缩算法,结合 SIREN 和位置编码的元学习,首次在柯达上以 2 倍的降维性能优于 JPEG2000 和率失真自动编码器,并缩小了全分辨率图像的差距。为了强调基于 INR 的源压缩的通用性,我们进一步进行了 3D 形状压缩实验,我们的方法大大优于传统压缩算法 Draco。
1. Introduction
生活在一个数字化无处不在、重要决策都基于大数据分析的世界里,如何有效地存储信息的问题比以往任何时候都更加重要。源压缩是以紧凑形式表示数据的通用术语,它要么保留所有信息(无损压缩),要么牺牲一些信息以获得更小的文件大小(有损压缩)。它是处理每天从互联网上传、传输和下载的大量图像和视频数据的关键组成部分。虽然无损压缩可以说是更可取的,但它有一个基本的理论极限,即香农熵[47]。因此,有损压缩的目的是在文件的质量和大小之间进行权衡,即所谓的速率失真权衡。
除了针对特定数据模式(如音频、图像或视频)进行调整的传统手工设计算法外,机器学习研究最近通过利用神经网络的力量开发了有前途的学习方法来进行源压缩。这些方法通常建立在众所周知的自动编码器[28]上,通过实现它的约束版本。这些所谓的率失真自动编码器(RDAEs)[5,6,37,25]共同优化了解码数据样本的质量及其编码文件的大小。
这项工作避开了 RDAEs 的流行方法,并研究了一种新的源压缩范例-特别是关注图像压缩。最近,隐式神经表示(INRs)作为一种灵活的、多用途的数据表示而受到欢迎,它能够在图像[49]、3D形状[44,49]和场景[40]上生成高保真的样本。一般来说,INR 通过学习网格坐标与相应数据值(例如RGB值)之间的映射来表示位于底层规则网格上的数据,并且甚至被假设为产生良好压缩的表示[49]。由于它们的通用性和早期利用它们进行压缩的并行尝试[19,11,20],INR 是一种很有前途的通用压缩算法。
目前,基于 INR 的压缩算法面临两个主要挑战:(1)直接的方法甚至难以与最简单的传统算法竞争[19]。(2)由于INRs通过对特定实例的过拟合来编码数据,因此编码时间被认为是不切实际的。为此,我们作出两点贡献。首先,我们提出了基于 INR 压缩的元学习。我们利用基于模型不确定元学习(Model-Agnostic meta-learning, MAML)[22]的 INRs 元学习的最新进展[48,52],找到可以用更少的梯度更新压缩数据并产生更好的率失真性能的权重初始化。其次,将 SIREN 与位置编码相结合进行基于INR 的压缩,大大提高了码率失真性能。虽然我们关注的是图像,但我们强调,我们提出的方法可以很容易地适应任何基于坐标的数据模式。总的来说,我们引入了一个压缩管道,它大大优于最近提出的 COIN[19],并且与传统的图像压缩算法相竞争。此外,我们证明了元学习 INRs 在下采样图像上的性能已经优于 JPEG2000 和一些 RDAEs。最后,通过直接将我们的方法应用于 3D 数据压缩,我们强调了基于 INR 的图像压缩的通用性,我们优于传统的 Draco 算法。
2. Related Work
Learned Image Compression. 学习图像压缩在[6]中引入,提出了端到端自编码器和熵模型,共同优化速率和失真。接下来,[7]通过添加尺度超先验扩展了该方法,然后[41,37,33]提出使用自回归熵模型来进一步提高压缩性能。后来,Hu等人[29]提出了一种从粗到细的分层超先验,Cheng等人[14]通过添加注意模块和使用高斯混合模型(Gaussian Mixture Model, GMM)来估计潜在表征的分布,实现了进一步的改进。目前的技术水平是由[58]实现的:他们提出了一个可逆卷积网络,并将残差特征增强作为预处理和后处理。此外,针对可变速率压缩的方法也很多,主要有基于 RNN 的自编码器[54,55,30]和条件自编码器[15]。此外,[4,38]提出使用生成对抗网络(GAN)进行图像压缩以优化感知质量。
Implicit Neural Representations. 关于 INR 的早期工作之一是 DeepSDF[45],它是 3D 形状的神经网络表示。特别地,他们使用有符号距离函数(SDF)通过一个场来表示形状,其中空间中的每个点都保持到形状表面的距离。在 DeepSDF 的同时,许多作品提出了类似的方法来用 INR 表示 3D 形状,例如占用网络[39]和隐式场解码器[13]。此外,INR 还被用于场景表示[40]、图像表示[12,50]和紧凑表示[17]。
Model Compression. 在过去的几十年里,有大量关于模型压缩的工作[36]。例如,[26]提出在步骤之间依次应用剪枝、量化和熵编码,并结合再训练。后来,[2]提出了一种使用速率扭曲目标的端到端学习方法。为了优化量化下的性能,一些研究[24,57,18,56]使用了混合精度量化,而其他研究[31,21,10,35,43,42]则提出了后量化优化技术。
Model Weights for Instance-Adaptive Compression. 最近,[46]建议在每个实例的基础上微调 RDAE 的解码器权重,并将权重更新附加到潜在向量上,从而改进 RDAEs。它与我们的工作有关,因为模型权重包含在表示中,然而 RDAE 体系结构与我们的根本不同。最近,Dupont等人[19]提出了第一种基于 INR 的图像压缩方法 COIN,该方法过拟合 INR 的模型权重来表示单个图像,并使用量化方法压缩 INR。重要的是,COIN 不使用元学习来初始化 INR、SIREN 的位置编码、后量化再训练和熵编码。此外,[9]最近提出了一种基于压缩 NeRF 权重的全场景压缩算法[40]。此外,并发 NeRV[11]提出使用 INR 压缩视频。虽然他们使用另一种数据模式,既不使用后量化再训练,也不使用元学习初始化,但他们的工作显示了基于 INR 的基于坐标的数据压缩的潜力。在另一项并行工作中,[20] 也提出将元学习应用于基于 INR 的压缩,以扩展 COIN。然而,与这项工作不同的是,它们在柯达的全分辨率图像上并不优于 JPEG。它们的性能与我们的方法相似,没有元学习和位置编码(见图7)。
3. Method
3.1 Background
INRs 通过将数据表示为从坐标到值的连续函数来存储基于坐标的数据,例如图像、视频和 3D 形状。例如,图像是水平和垂直坐标 ( p x , p y ) (p_x, p_y) (px,py) 的函数,并映射到颜色空间 (如 RGB) 中的颜色向量:
![]()
这种映射可以用一个神经网络 f θ f_θ fθ 来近似,通常是一个带有参数 θ θ θ 的多层感知器 (MLP),使得 I ( p x , p y ) ≈ f θ ( p x , p y ) I(p_x,p_y)≈f_θ(p_x,p_y) I(px,py)≈fθ(px,py)。由于这些函数是连续的,INR 是分辨率无关的,即它们可以在归一化范围内的任意坐标上求值 [−1,1]。为了表示基于像素的图像张量 x x x,我们在均匀间隔的坐标网格 p p p 上评估图像函数,使得 x = I ( p ) ∈ R W × H × 3 x=I(p)\in\mathbb{R}^{W×H×3} x=I(p)∈RW×H×3
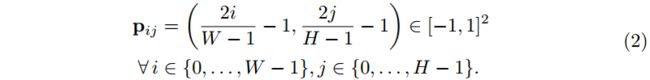
注意,每个坐标向量都是独立映射的:
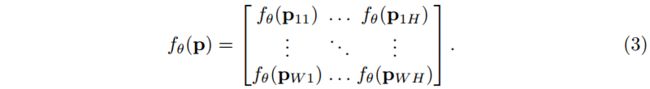
Rate-distortion Autoencoders. 学习源压缩的主要方法是 RDAEs: 编码器网络产生压缩表示,通常称为潜在向量 z ∈ R d z\in\mathbb{R}^d z∈Rd,联合训练的解码器网络使用它来重建原始输入。早期的方法通过限制 z z z 的维数 d d d 来增强 z z z 的紧密性[27]。较新的方法通过在损失中加入一个熵估计,即所谓的率损失,来约束这种表示。反映 z z z 的存储要求的速率项与量化压缩误差的失真项一起最小化。
3.2 Image Compression using INRs
与 RDAEs 相比,INR 将所有信息隐式地存储在网络权重 θ θ θ 中。INR 本身的输入,即坐标,不包含任何信息。编码过程相当于训练 INR。解码过程相当于将一组权重加载到网络中,并在坐标网格上进行评估。我们可以总结为:
![]()
因此,我们只需要存储 θ ∗ θ^* θ∗ 来重建原始图像 x x x 的扭曲版本。在我们的方法中,我们描述了一种寻找 θ ∗ θ* θ∗ 的方法,以同时实现紧凑的存储和良好的重建。
Architecture. 我们使用了[49]中最初提出的 SIREN,即使用频率 ω = 30 ω=30 ω=30 的正弦激活的 MLP,该方法最近在图像数据上显示出良好的性能。我们采用了作者建议的初始化方案。由于我们的目标是在多个比特率下评估我们的方法,因此我们改变模型大小以获得速率失真曲线。我们还提供了关于如何改变模型大小以实现最佳速率失真性能 (参见补充材料) 和 INR 架构 (参见第4.4节) 的简要介绍。
Input Encoding. 输入编码将输入坐标转换到更高的维度,这已被证明可以提高感知质量[40,53]。值得注意的是,据我们所知,我们是第一个将 SIREN 与输入编码结合起来的人——以前的输入编码只用于基于整流线性单元 (ReLU) 激活函数的 INR。我们应用了[40]中提出的位置编码的改编版本,其中我们引入尺度参数 σ σ σ 来调整频率间隔 (类似于[53]),并将频率项与原始坐标 p p p 连接起来 (如 SIREN codebase1):
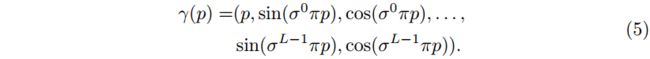
其中 L L L 是所用频率的个数。我们将在第4.4节研究输入编码的影响。
3.3 Compression Pipeline for INRs
本节介绍基于 INR 的压缩管道。首先,我们描述了基于随机初始化 INR 的基本方法(第3.3节)。然后,我们提出元学习初始化来改善基于 INR 压缩的率失真性能和编码时间(第3.3节)。整个管道如 图2 所示,更高层次的概述如 图1 所示。
Basic Approach using Random Initialization.
Stage 1: Overfitting.
首先,我们在测试时对数据样本进行 INR f θ f_θ fθ 过拟合。这相当于调用其他学习方法的编码器。我们称这个步骤为过拟合,以强调 I N R INR INR 被训练成只代表单个图像。给定图像 x x x 和坐标网格 p p p,我们最小化目标:
![]()
我们使用均方误差(MSE)作为损失函数来衡量真值目标与 INRs 输出的相似度:
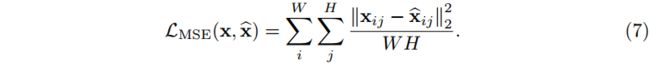
注意 x i j ∈ R 3 x_{ij}∈\mathbb{R}^3 xij∈R3 是单个像素的颜色向量。
Regularization. 在图像压缩中,我们的目标是同时最小化失真 (例如,MSE) 和比特率。由于模型熵不可微,不能直接用于梯度优化。文献中使用的一种方法是在训练期间使用可微熵估计器[2]。然而,我们选择使用一个正则化项,它近似地诱导出较低的熵。特别地,我们将 L1 正则化应用于模型权重。总的来说,这产生了以下优化目标:
![]()
其中 λ λ λ 决定了引起稀疏性的 L1 正则化的重要性。我们的正则化项与[46]中使用的稀疏性损失有关:我们有限制权重熵的相同目标,但是我们将其应用于 INR,而他们将其应用于传统的显式解码器。
Stage 2: Quantization. 通常,过度拟合产生的模型权重是单精度浮点数,每个权重需要 32 位。为了减少内存需求,我们使用AI模型效率工具包(AIMET)量化权重1。我们采用特定于每个权重张量的量化,使均匀间隔的量化网格调整到张量的值范围。位宽决定了离散级别的数量,即量化箱。我们从经验上发现,在7-8范围内的位宽导致我们的模型的最佳速率失真性能,如补充所示。
Stage 3: Post-Quantization Optimization. 量化通过将权重四舍五入到最接近的量化仓来降低模型的性能。我们利用两种方法来减轻这种影响。首先,我们使用AdaRound[42],这是一种二阶优化方法来决定是向上还是向下舍入权重。其核心思想是传统的最接近四舍五入并不总是最佳选择,如[42]所示。随后,我们使用量化感知训练(QAT)对量化权重进行微调。这一步的目的是扭转部分量化误差。量化是不可微的,因此我们依靠直通估计器(STE)[8]进行梯度计算,基本上绕过了反向传播期间的量化操作。
Stage 4: Entropy Coding. 最后,我们执行熵编码来进一步无损压缩权重。特别地,我们使用二值化算术编码算法对量化权重进行无损压缩。
Meta-learned Initializations for Compressing INRs. 直接将 INR 应用于压缩有两个严重的限制:首先,它需要在编码步骤中从头开始对数据样本进行过拟合。其次,它不允许在压缩算法中嵌入归纳偏差 (例如,特定图像分布的知识)。为此,我们应用元学习,即模型不可知元学习(Model Agnostic Meta-Learning, MAML)[23]来学习接近权重值的权重初始化,并包含图像分布的信息。先前关于 INR 元学习的研究主要是为了提高收敛速度[52]。学习到的初始化 θ 0 θ_0 θ0 被认为在权重空间上更接近最终的 INR。我们想利用这个事实来压缩假设更新 ∆ θ = θ − θ 0 ∆θ=θ-θ_0 ∆θ=θ−θ0 比权重张量 θ θ θ 需要更少的存储空间。因此,我们固定 θ 0 θ_0 θ0 并将其包含在解码器中,这样就足以传输 ∆ θ ∆θ ∆θ,或者更准确地说,是量化的更新 ∆ θ ~ ∆\widetilde{θ} ∆θ 。解码器然后可以通过计算重建图像:
![]()
我们预计权重更新所占的值范围 ∆ θ ∆θ ∆θ 明显小于全权重 θ θ θ。因此,在量化权重更新时,最低和最高量化仓之间的范围可以更小。在固定的位宽下,在权重更新的情况下,量化箱之间的步长将更小,因此,平均舍入误差也更小。
注意,在过拟合单个图像之前,每个分布 D \mathcal{D} D 只学习一次初始化。因此,我们把它称为阶段 0。阶段 0 发生在训练时,在许多图像上执行,不是推理的一部分。阶段 1-4 发生在推理时间,目的是压缩单个图像。因此,使用元学习初始化不会增加推理时间。
Integration into a Compression Pipeline. 当我们只想编码更新 ∆ θ ∆θ ∆θ 时,我们需要相应地调整压缩管道。在过拟合期间,我们将目标更改为:
![]()
因此,正则化项现在诱导模型权重保持接近初始化。同样,我们直接将量化应用于更新 ∆ θ ∆θ ∆θ。为了执行 AdaRound 和 QAT,我们对 MLP 中的所有线性层进行分解,以从更新中分离初始值:
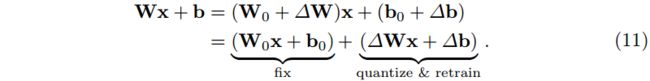
这是必要的,因为优化舍入和 QAT 需要每个线性层的原始输入输出函数。将其分成两个平行的线性层,我们可以固定包含 W 0 W_0 W0 和 b 0 b_0 b0 的线性层,并对更新参数 ∆ W ∆W ∆W 和 ∆ b ∆b ∆b 应用量化、AdaRound 和 QAT。
INRs for 3D Shape Compression. 所提出的基于 INR 的压缩管道在修改最小的情况下适用于任何基于坐标的数据模式。我们为 3D 形状演示了这一点。三维形状可以表示为带符号的距离函数:
![]()
也就是说,我们在 3D 空间中的每个点 ( p x , p y , p z ) (p_x, p_y, p_z) (px,py,pz) 和形状表面之间分配一个带符号的距离 d d d。这里,距离的符号表示我们是在形状的内部(负)还是外部(正)。我们现在可以简单地训练我们的 INR 来近似 SDF:
![]()
当训练 INR 来估计 SDF 时,最重要的是接近 GT 的准确预测。因此,我们采用[51]中提出的抽样策略。
4 Experiments
Datasets. 柯达[1]数据集是包含各种物体、人物或风景的 24 张图像的集合。该数据集的分辨率为 768×512 像素(垂直×水平)。[3]中介绍的 DIV2K 数据集包含 1000 张高分辨率图像,宽度约为 2000 像素。数据集分为 800 个训练图像,100 个验证图像和 100 个测试图像。为了元学习初始化的目的,我们将 DIV2K 图像调整为与柯达(768 × 512)相同的分辨率。CelebA[34] 是一个包含超过 20 万张名人图像的数据集,分辨率为 178×218。我们在测试集中随机抽取的 100 张图像上评估我们的方法。对于我们的 3D 形状压缩实验,我们使用来自斯坦福 3D 扫描存储库[16]的 5 个高分辨率网格,我们在训练之前将其归一化,以便它们适合一个单位立方体。更多细节见附录。
Metrics. 我们评估了两个指标来分析速率和失真方面的性能。我们用存储表示所需的总比特数除以图像的像素数 W·H 来衡量速率:
![]()
我们根据 MSE 测量失真,并使用公式将其转换为峰值信噪比(PSNR):
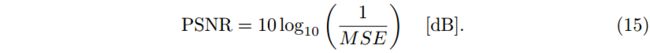
Baselines. 我们将我们的方法与传统的编解码器、基于 INR 的压缩和基于 RDAEs 的学习方法进行了比较。
- 传统的图像压缩编解码器:JPEG, JPEG2000, BPG
- 基于INR的图像压缩:Dupont等[19] (COIN)
- 基于RDAE的图像压缩:Balle等[6],Xie等[58]
- 3D网格压缩:Draco
Optimization and Hyperparameters. 除非另有说明,否则我们在整个实验部分中使用一组默认的超参数。特别是,我们使用具有 3 个隐藏层的 INR 和正弦激活,并结合使用 σ = 1.4 σ=1.4 σ=1.4 的位置编码。在更高分辨率的 Kodak 数据集上,我们将频率数设置为 L = 16 L=16 L=16,而在 CelebA 上,我们将 L = 12 L=12 L=12。
我们改变每层 M 的隐藏单元的数量,即 MLP 的宽度,以评估不同速率失真工作点的性能。我们将随机初始化的方法称为基本方法,而包含元学习初始化的方法称为元学习方法。我们发现元学习方法的最佳位宽为 b = 7 b=7 b=7,基本方法的最佳位宽为 b = 8 b=8 b=8。有关训练和超参数的更多细节,请参阅补充材料。
4.1 Comparison with State-of-the-Art
Full resolution. 图4 分别描述了我们在 CelebA/Kodak 上的结果。提出的基本方法在整个比特率范围内已经明显优于 COIN。对于大多数比特率,它也比 JPEG 更好,除了 CelebA 上的最高设置。通过我们提出的元学习方法,我们可以在所有比特率上改进基本方法。在这两个数据集之间, CelebA 数据集上的差异明显更大。在最低比特率下,元学习方法达到了 JPEG2000 的性能,但是我们的方法在更高比特率下无法跟上 JPEG2000。在 CelebA 数据集上,元学习方法也几乎达到了具有分解先验[6]的自编码器在较低比特率下的性能。面对更高的比特率,自动编码器的优势变得更加明显。在这两个数据集上,BPG 和最先进的 RDAE[58] 明显优于我们的方法。
Reduced image resolution. 我们进一步将我们的基本方法和元学习方法与柯达分辨率降低 (2x/4x) 的其他方法进行比较。这些图像由 384×256 像素组成。192×128 像素。我们观察到元学习方法再次比基本方法表现得更好。此外,我们的元学习方法在整个比特率范围内的图像分辨率表现优于BPG和Xie等人以外的所有其他方法。
4.2 Visual Comparison to JPEG and JPEG2000
我们将元学习方法的压缩图像与 图6 中的 JPEG 和 JPEG2000 编解码器进行了比较。我们在视觉上证实了我们的模型比 JPEG 有显著的改进:我们的模型产生了一个整体上更令人愉悦的图像,具有更好的细节和更少的伪影,尽管我们在两个图像上都以更低的比特率操作。对于 图6 中的柯达图像,与 JPEG2000 相比,我们在相同失真下实现了略低的比特率。从视觉上看,JPEG2000 图像在边缘周围和高频细节区域显示出更多的伪影。然而,由于我们的模型引入了周期性伪影,天空在 JPEG2000 图像上渲染得更好。对于 图6 中的 CelebA 图像,我们的方法实现了比 JPEG2000 图像更低的比特率和更高的 PSNR。JPEG2000 再次显示了边缘周围的伪影(例如背景中的字母周围),并平滑了面部从较亮到较暗区域的过渡。我们的方法产生了更自然的音调过渡。
4.3 Convergence Speed
在 图5 中,我们展示了基本方法和元学习方法在不同时代数量上的比较。特别是在过拟合开始时,元学习方法的收敛速度明显加快。在前 3 次迭代之后,我们已经获得了比基本方法在 50 次迭代之后获得的更好的性能。当我们接近各自模型的最终性能时,收敛速度会减慢,而元学习方法保持优势:它在 2500 次迭代后达到与基本方法在 25000 次迭代后相同的性能。这相当于减少了 90% 的训练时间。
4.4 Choosing Input Encoding and Activation
一个重要的架构选择是输入编码和所使用的激活函数的组合。我们与[53]中提出的高斯编码进行比较。对于这种编码,我们使用与[53]中相同数量的频率作为隐藏维度(L = M),标准差 σ = 4 σ=4 σ=4。我们使用正则化参数 λ = 1 0 − 6 λ=10^{−6} λ=10−6 从随机初始化开始,在 Kodak 数据集上训练具有不同隐藏维数(M∈{32,48,64,96,128})和不同输入编码的模型。
查看 图7a,与 图7b 相比,我们可以看到正弦激活在每种配置中都优于 ReLU 激活,特别是在更高比特率时。对于两个激活,最好的整体输入编码是位置编码,而不是高斯编码。没有输入编码和正弦激活的 MLP (SIREN架构)的性能明显优于其对应的 ReLU 模型,但仍然无法达到带有输入编码的模型的性能。
重要的是,我们研究了位置编码是否在一般情况下改善了 SIREN,或者更确切地说,是使它对量化更具鲁棒性。因此,我们测量了我们的基本方法在不同比特宽度下的量化误差。结果如图8所示。当用位置编码训练时,ReLU 和正弦激活都显示出减少的量化误差。然而,在 SIREN 的情况下,效果最为明显。对比 图8 和 图7b 中位置编码前后 SIREN 的 PSNR-delta,可以发现位置编码使得 SIREN 对量化的鲁棒性明显增强。
4.5 3D Shape Compression
为了证明我们的算法适用于图像以外的基于坐标的数据,我们提供了一个额外的实验来展示它在 3D 形状压缩任务上的性能。由于本实验的主要目标是展示基于 INRs 的压缩的可移植性,我们只训练了我们的基本方法,而没有对 3D 形状进行元学习。我们根据 图9 中所需的存储绘制了所有形状的平均倒角距离,并与基于网格量化的 Draco 算法进行了比较。我们将重点放在与基于网格的压缩算法的比较上,因为它们也保留了一个连续的表面,而不像点云压缩的替代方法。我们需要比 Draco 更少的比特来编码类似质量的形状。关于这个实验的进一步细节见附录。
5 Conclusion
总的来说,INR 作为图像的压缩表示显示了巨大的潜力。我们的主要贡献是使用元学习初始化和 SIREN 与位置编码相结合,与之前基于 INRs 进行图像压缩的方法[19]相比,大大提高了率失真性能。此外,我们的方法是第一个基于INRs 的方法,在很大一部分比特率上与传统编解码器竞争。
6 Acknowledgements
这项工作得到了谷歌的部分支持。
7. Supplementary Material
在7.1节中,我们提供了元学习算法的描述,在7.2节中,我们详细解释了如何从元学习初始化开始过拟合。我们在第7.3节中阐述了我们的架构选择,并在第7.4节中展示了 L1 正则化的影响。关于量化位宽的影响和元学习初始化的泛化潜力的其他研究分别在第7.6节和第7.7节中展示。我们的方法,JPEG 和 SOTA RDAEs 之间的进一步运行时比较将在7.8节中给出。在第7.9节中,我们对压缩管道不同阶段中使用的超参数进行了完整的概述。最后,我们提供了额外的定性示例,将我们的方法与第7.10节中的 JPEG 和 JPEG2000 以及第7.11节中的 Draco 进行比较。
7.1 Meta-Learning Algorithm
隐式神经表征的元学习初始化 算法1 是[48]中提出的算法的改编版本。我们修改了符号与我们的相匹配,并将目标改为图像回归而不是符号距离函数回归。==通常,该算法由两个循环组成,外循环(第7-15行)和内循环(第11-13行)。外部循环索引 i i i 表示为上标,而内部循环索引 j j j 表示为下标。外部循环执行预定义的迭代次数 n n n。首先,我们从数据分布中采样图像 x i x_i xi。然后,我们定义一个坐标向量 p p p,其坐标网格的分辨率与图像 x i x_i xi 相同。我们将内环参数 φ 0 i φ_0^i φ0i 初始化为当前的外环参数 θ θ θ。对于 i = 1 i=1 i=1,这只是随机初始化,之后这些是元学习参数。我们在第 9 行开始内循环。对于 k 次迭代,我们计算图像 x i x_i xi 和由内环参数 ϕ j i ϕ_j^i ϕji 参数化的 INR 输出之间的 MSE 损失。在第 13 行,我们对内部循环参数执行梯度更新。 α α α 包含内环梯度更新的学习率。一个简单的选择是对 φ j i φ_j^i φji 中的所有参数使用相同的静态学习率。元学习的强大之处在于,我们也可以对内循环的学习率进行元学习,因此 α α α 和 θ θ θ 一样是一个优化变量。我们可以更进一步,通过
- List item
元学习每个内部循环参数和每个步骤 j j j 的学习率。这种变体被作者[48]称为每个参数每个步骤学习率类型。我们有效地学习的学习率是模型参数的 k k k 倍。我们在第13行使用Hadamard乘积来表示 α α α 中的学习率和梯度之间的乘积是按分量执行的。下标 j j j of α α α 表示我们在每一步 j j j 中有不同的学习率==。
经过 k k k 次内循环迭代后,我们重新计算最后一步内循环参数的损失。在第15行,我们对元学习模型参数和学习率 α α α 进行梯度更新。这是梯度的梯度:反向传播应用于内部循环的计算图,它本身包含内部循环梯度更新。我们继续第 8 行,对下一个图像进行采样,并重复这个过程。在所有外部循环完成后,我们返回元学习权值 θ θ θ 和学习率 α α α。
7.2 Overfitting from Meta-Learned Initializations
在过拟合阶段的开始,我们利用从元学习中获得的参数学习率。基本上,我们只运行一次内部循环,就像 算法2 中显示的那样,只需 k = 3 k=3 k=3 步就可以接近最终图像。然后我们继续和 Adam 一起优化。此时,Adam 优化器的动量项未初始化。我们发现,在 100 个 epoch 的预热阶段线性增加学习率可以防止重构质量的初始退化,甚至可以提高更高比特率下的最终性能(见 图10)。
7.3 Number of Layers and Hidden Dimension
当使用基于 MLP 的网络时,重要的架构选择是隐藏层的数量和隐藏单元的数量。对于 MLP,深度或宽度都直接影响参数的数量,并间接影响比特率。换句话说,有两种扩展网络的方法。我们使用我们的基本方法和 λ = 1 0 − 6 λ=10^{−6} λ=10−6来检查 图11 中隐藏单元 ( M ∈ { 32 , 48 , 64 , 96 , 128 } ) (M\in\{32,48,64,96,128\}) (M∈{32,48,64,96,128}) 和隐藏层 ( { 2 , . . . , 8 } ) (\{2,...,8\}) ({2,...,8}) 的各种组合的率失真性能。从两幅图中我们可以看出,层数的增加最终会导致收益递减:比特率不断增加,而 PSNR 的增益很小。在较低的位宽 b = 7 b=7 b=7 时,隐藏层数量较多的平坦化更加明显。这里的量化噪声更强,随着深度的增加,噪声可能会被放大,从而限制性能。我们得出的结论是,相对于模型的宽度,速率失真性能的尺度更优雅。然而,我们也注意到,最低设置的 2 个隐藏层通常优于具有更少隐藏单元和更多层的网络。
7.4 Impact of L1 Regularization.
在这个实验中,我们试图验证 L1 正则化是否对性能有有益的影响。我们使用从随机初始化开始的默认参数进行训练,并在[0,10−4]范围内改变 λ λ λ。
在 图12 中,我们观察到 λ = 1 0 − 5 λ = 10^{−5} λ=10−5 的值在较高比特率下比较低的 λ λ λ 值具有更好的性能。性能改进表现为比特率的降低,这支持了 L1 正则化可以导致熵降低的说法。当正则化强度增大到 λ = 1 0 − 4 λ= 10^{−4} λ=10−4 时,对权重的限制过大,导致性能不如 λ = 1 0 − 5 λ=10^{−5} λ=10−5。因此,L1 正则化可以帮助减少熵,但需要与架构大小的修改相结合,以实现良好的速率失真权衡。
7.5 Post-Quantization Optimization.
我们比较了不同后量化优化设置的元学习方法。图13 显示了在 Kodak 上评估的性能差异。我们看到 AdaRound 和再训练的应用带来了持续的改进。然而,在整个比特率范围内,最好的选择是结合使用这两种方法。
7.6 Influence of Quantization Bitwidth
我们在 图14 中展示了位宽对元学习方法的率失真性能的影响,在 图15 中展示了基本方法。对于元学习方法,7 位是两个数据集的最佳选择。然而,对于基本方法,8 位量化优于更低的位宽。然而,在柯达数据集上,7 位和 8 位量化之间的差异非常小。我们还用虚线显示了 4 个具有不同隐藏单元数量的 MLP 的非量化性能。我们看到,对于 8 位宽,我们几乎可以在大多数配置中达到非量化性能。
7.7 Generalization of Meta-Learned Initializations
我们想要证明元学习初始化能够推广到分布外的图像,即使元学习数据集只包含相似的图像。为此,我们最小限度地裁剪和调整柯达图像到与CelebA (178×218)相同的分辨率和宽高比,然后使用从CelebA获得的元学习初始化压缩它们。在 图16 中,我们展示了元学习方法仍然优于基本方法。
7.8 Further Runtime Comparison
在本文中,我们通常训练模型直到完全收敛,因此我们优化了最佳的率失真性能。为了表明我们的方法可以调整为快速运行时,我们将编码/解码运行时(在[s]中)与 JPEG 和 Xie 等人[58]在 表1 中进行了比较,在率失真性能至少与 JPEG 匹配的约束下。因此,我们在性能和运行时间之间进行权衡。
7.9 Detailed Training Hyperparameter Overview
在本节中,我们将提供所有超参数的完整概述。我们还在相应的小节中提到具体到培训程序的细节。
Image Compression Hyperparameters
Architecture. 我们在 表2 中总结了默认的体系结构超参数。对于全分辨率的 Kodak 和 CelebA 图像,我们分别使用 M∈{32,48,64,128} 和 M∈{24,32,48,64} 来评估我们的方法。对于半分辨率(2x比例)的柯达图像,我们使用 M∈{8,16,32,48},并将输入频率的数量减少到 L = 12。对于四分之一分辨率(4倍比例)的柯达图像,我们使用 M∈{4,8,16,32},并进一步将输入频率的数量减少到 L = 10。
Meta-Learning the Initializations. 在表3中,我们列出了用于元学习初始化的超参数的默认值。我们使用学习率计划,当在最后一次(10 =耐心)验证中没有改进时,将学习率减半。为了验证,我们使用从各自数据集的验证集中采样的100张图像的子集,在我们的示例中是CelebA或DIV2K。我们通过对验证子集中的每个图像运行内循环优化来计算验证损失。计算验证损失涉及到内循环训练,这是我们将验证集大小限制为 100 的原因。当我们在 CelebA 上训练初始化时,我们训练1个epoch。当使用DIV2K数据集时,我们训练了30个epoch,因为它是一个明显较小的数据集。最后,我们保存了实现最低验证损失的初始化。
Overfitting. 过拟合阶段的默认超参数如 表4 所示。如果没有提到的话,我们在所有实验中都使用这些超参数。特别是,我们在降低分辨率的实验中不使用 L1 正则化。由于我们是过拟合的,所以我们在训练图像本身上进行验证。如果在过去的 500 次迭代中损失没有改善,我们将学习率降低 0.5 倍。注意,1 epoch 等于 1 个优化步骤,换句话说,一个训练批包含我们过拟合的图像的所有像素。我们训练了 25000 次,以确保我们测试的每个架构和配置都有机会达到收敛。正如预期的那样,较小的模型通常更快地达到峰值性能。如果损失在过去 5000 次中没有改善,我们就停止训练,以防止不必要的计算资源使用。最后,我们返回在过拟合过程中损失最小的模型参数。
Quantization, Post-Quantization Optimization & Entropy Coding. 在表5中,我们显示了量化和比特流编码相关阶段的默认值。我们强调默认情况下我们使用 AdaRound 和 QAT 的组合。
MetaSDF: Meta-learning Signed Distance Functions
Abstract
神经隐式形状表示是一种新兴的范式,与传统的离散表示相比,它提供了许多潜在的好处,包括在高空间分辨率下的记忆效率。用这种神经隐式表示对形状进行泛化相当于在各自的函数空间上学习先验,并能够从部分或有噪声的观察中重建几何形状。现有的泛化方法依赖于将神经网络条件化在一个低维潜在码上,该码要么由编码器回归,要么在自解码器框架中共同优化。在这里,我们将形状空间的学习形式化为一个元学习问题,并利用基于梯度的元学习算法来解决这个任务。我们证明了这种方法的性能与基于自动解码器的方法相当,同时在测试时推理方面快了一个数量级。我们进一步证明,所提出的基于梯度的方法优于利用基于池的集编码器的基于编码器-解码器的方法。
1 Introduction
人类对 3D 形状有着令人印象深刻的直觉;对一个物体进行局部观察,我们可以很容易地想象出整个物体的形状。长期以来,计算机视觉和机器学习研究人员一直试图用算法重现这种能力。新兴的一类神经隐式形状表示,例如使用由神经网络参数化的有符号距离函数,有望通过学习神经隐式形状空间上的先验来实现这些能力[1,2]。在这种方法中,每个形状由一个函数 Φ Φ Φ 表示,例如,一个带符号的距离函数。因此,在一组形状上进行泛化相当于在这些函数的空间上学习一个先验 Φ Φ Φ。出现了两个问题:(1)我们如何参数化函数 Φ Φ Φ,以及(2)我们如何在给定一组(部分)观测值的情况下推断这样一个 Φ Φ Φ 的参数?
现有的方法假设函数空间 Φ Φ Φ 是低维的,并将每个形状表示为一个潜在的代码,该代码通过基于连接的条件反射或超网络来参数化整个函数 Φ Φ Φ。这些潜在代码要么由 2D 或 3D 卷积编码器直接推断,要么以单个图像或经典体积表示作为输入,要么通过自动解码器框架,其中每个训练样本的单独潜在代码在训练时被视为自由变量。卷积编码器虽然速度快,但需要在规则网格上进行观察,并且与 3D 变换不相等[3]。此外,它们并没有提供一种直接的方法来从可变数量的观测中积累信息,通常采用观察点潜在代码的排列不变池化[4]。最近提出的基于池的集合编码器可以编码可变基数的集合[5,6],但已经发现不适合上下文。理论证据也证实了这一点,即为了保证嵌入函数的普适性,嵌入的维数至少需要上下文点的个数[7]。在实践中,大多数方法都利用自动解码器框架进行泛化,这与观测值的数量无关,也不需要在规则网格上进行观测。这在几何、外观和语义属性的少量重建上取得了令人印象深刻的结果[8,9]。
要从测试时的一组观察结果推断出单个 Φ Φ Φ 的参数,基于编码器的方法只需要向前传递。相比之下,自动解码器框架不学习从观察中推断嵌入,而是需要在测试时解决优化问题以找到低维潜在嵌入,即使对于简单的场景,例如 ShapeNet 数据集中的单个 3D 对象,这也可能需要几秒钟。
在这项工作中,我们确定了神经隐式函数空间学习和元学习之间的关键联系。然后,我们建议利用最近提出的基于梯度的元学习算法来学习形状空间,这比基于编码器和自动解码器的方法都有好处。具体来说,所提出的方法与基于自动解码器的模型相当,同时在推理时间上快一个数量级,不需要在规则网格上观察,自然地与可变数量的观察相结合,优于基于池的集编码器方法,并且不需要假设低维潜在空间。
2 Related Work
Neural Implicit Scene Representations. 场景的隐式参数化是机器学习社区感兴趣的新兴主题。这些连续表示被参数化为多层感知器,可以应用于形状零件[10,11]、物体[1,12 - 14]或场景[8,15,16]的建模。这些和相关的神经隐式通常是从 3D 数据中训练的[1,2,12 - 18],但最近的工作也表明如何直接使用 2D 图像数据来监督训练过程[8,19 - 21],利用可微神经渲染[22]。早期在合成模式生成网络上的工作探索了类似的策略来参数化 2D 图像[23,24]。
Learning shape spaces. 大量先前的工作已经探索了经典几何表示参数的先验学习,如网格、体素网格或点云[5,25 - 27]。然而,学习几何的神经隐式表示的先验,需要学习函数空间的先验。为此,现有的工作假设了一个低维的潜在形状空间,并利用自动解码器或卷积编码器来回归潜在嵌入。然后通过基于连接的条件作用[1,2]或通过超网络[8,28]将这种嵌入解码为一个函数。在这项工作中,我们提出了一种基于元学习的方法来学习有符号距离函数的形状。
Meta-Learning. 元学习通常在少量学习的背景下形式化。在这里,目标是训练一个学习者,它可以快速适应新的、看不见的任务,只有很少的训练例子,通常被称为上下文观察。一类元学习器提出学习优化器或更新规则[29-31]。条件和注意神经过程[4,6,32]通过排列不变集编码器将上下文观察编码为低维嵌入,解码网络取决于由此产生的潜在嵌入。最近的一类算法提出学习神经网络的初始化,然后通过梯度下降的几个步骤将其专门用于新任务[33,34]。这类算法最近引起了相当大的兴趣,导致了各种各样的扩展和改进。Rusu等[35]通过在潜在空间中进行优化,混合了前馈和基于梯度下降的专门化。Rajeswaran等人[36]提出通过隐式方法获得梯度,而不是通过内循环的展开迭代进行反向传播,从而显著节省内存。在这项工作中,我们利用这类基于梯度下降的元学习器来解决形状空间的学习问题。我们建议读者参考最近的一份调查报告,以获得详尽的概述[37]。
3 Meta-learning Signed Distance Functions
我们感兴趣的是学习隐式形状表征的先验。如[1]所示,我们考虑一个包含 N N N 个形状的数据集 D D D。
![]()
其中 x j x_j xj 是空间坐标, s j s_j sj 是这些空间坐标上的带符号距离。我们的目标是通过使用神经网络 Φ i Φ_i Φi [1]直接逼近其 SDF 来表示形状,该神经网络隐式地将形状的 GT 表示为其零水平集 L 0 ( Φ i ) L_0(Φ_i) L0(Φi):
![]()
我们也可以选择近似点的二进制“占用”,而不是它们的带符号距离; 然后,该表面将由二元分类器的决策边界表示[2]。
在一组形状上进行泛化,就等于在函数空间 X \mathcal{X} X 上学习一个先验,其中 Φ i ∈ X Φ_i \in \mathcal{X} Φi∈X。出现了两个问题: (1)我们如何对集合 X \mathcal{X} X 的单个元素 Φ i Φ_i Φi 进行参数化,以及(2)在给定一组(部分)观测值 X i X_i Xi 的情况下,我们如何推断这样一个 Φ i Φ_i Φi 的参数?
Parameterizing Φ i Φ_i Φi: Conditioning via concatenation and hypernetworks. 现有的形状空间泛化方法依赖于对形状的潜在嵌入进行解码。在连接条件反射中,目标坐标 x x x 与潜在形状嵌入 z i z_i zi 连接,并被馈送到一个前馈神经网络,该网络的参数在所有形状实例中共享。潜在代码为共享网络的输出设定条件,并允许单个共享网络表示多个形状实例[1,2]。
在另一种公式中,我们可以使用超网络,它将潜在代码 z i z_i zi 作为输入并生成形状表示的 MLP, Φ i Φ_i Φi 的参数, Φ i Φ_i Φi 然后可以在坐标 x x x 处采样以产生输出带符号距离。正如我们在补充中所证明的那样,通过串联进行条件反射是超网络的一种特殊情况[28],其中超网络被参数化为单个线性层,该层仅预测网络的偏差 Φ i Φ_i Φi。事实上,最近的相关工作已经证明,将潜在代码 z i z_i zi 映射到 MLP Φ i Φ_i Φi 的所有参数的超网络也可以类似地用于学习形状空间[8]。
Inferring parameters of Φi from observations: Encoders and Auto-decoders. 现有的推断潜在形状嵌入的方法依赖于编码器或自动解码器。前者依赖于编码器,如卷积编码器或集合编码器,生成潜在嵌入,然后通过连接或超网络使用条件作用解码为隐式函数。
在自动解码器(即仅解码器)架构中,潜在嵌入被视为学习参数,而不是从训练时的观察中推断出来。在训练时,自动解码器框架支持跨一组形状的直接泛化。在测试时,我们冻结模型的权重,并执行搜索以找到符合一组上下文观察 X ^ \hat{X} X^ 的潜在代码 z ^ \hat{z} z^。自动解码器框架的一个主要缺点是解决这个优化问题很慢,每个对象需要几秒钟。
3.1 Shape generalization as meta-learning
元学习的目的是学习一个可以快速适应新任务的模型,可能只有有限的训练数据。当适应新任务时,模型被给予“上下文”观察,它可以通过梯度下降等方式修改自己。然后,经过调整的模型可以用来对看不见的“目标”观测结果进行预测。形式上,监督元学习假设任务 T ∼ p ( T ) \mathcal{T}\sim p(\mathcal{T}) T∼p(T) 上的分布,其中每个任务的形式为 T = ( L , { ( x l , y l ) } l ∈ C , { ( x j , y j ) } j ∈ T \mathcal{T} = (\mathcal{L}, \{(x_l,y_l)\}_{l\in C}, \{(x_j, y_j)\}_{j\in T} T=(L,{(xl,yl)}l∈C,{(xj,yj)}j∈T,具有损失函数 L \mathcal{L} L,模型输入 x x x,模型输出 y y y,属于上下文集 C C C 的所有指标的集合,属于目标集 T T T 的所有指标的集合。在训练时,绘制一批任务 T i T_i Ti,每个任务分为“上下文”和“目标”观察。该模型利用“上下文”观察结果进行自我调整,并根据“目标”观察结果做出预测。对模型参数进行优化,使所有任务中训练集中所有目标观测值的损失 L L L 最小化。
关键思想是将形状空间的学习视为元学习问题。在这个框架中,任务 T i T_i Ti 表示找到形状的带符号距离函数 Φ i Φ_i Φi 的问题。简单地说,通过给一个模型提供有限数量的“上下文”观测值,每个观测值都由世界坐标位置 x x x 和以距离为符号的 GT 值 s s s 组成,我们的目标是快速将其专门化,以近似底层 S D F i SDF_i SDFi。上下文和目标观测是来自特定对象数据集 X i : T i = T = ( L , { ( x l , y l ) } l ∈ C , { ( x j , y j ) } j ∈ T X_i:\mathcal{T}_i=\mathcal{T} = (\mathcal{L}, \{(x_l,y_l)\}_{l\in C}, \{(x_j, y_j)\}_{j\in T} Xi:Ti=T=(L,{(xl,yl)}l∈C,{(xj,yj)}j∈T 的样本。因为每个任务都包含一个有符号距离函数的拟合,我们可以选择一个全局损失,比如 l 1 \mathcal{l}_1 l1。

请注意,自动解码器框架也可以被视为元学习算法,尽管通常不会这样讨论。在这个视图中,自动解码器框架是一个异常值,因为它没有在前向传递中执行模型专门化。相反,专门化需要随机梯度下降直到收敛,在训练和测试时都是如此。
Learning a shape space with gradient-based meta-learning. 我们建议利用类 MAML 算法族[33]。因此,我们将特定于实例的 S D F i SDF_i SDFi(近似为 Φ i Φ_i Φi)视为具有参数 θ θ θ 的底层元网络的专门化。然后根据以下更新规则执行 k k k 个梯度下降步骤:
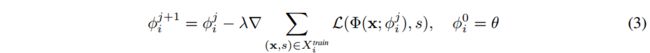
式中 φ I j φ^j_I φIj 为形状 i i i 在内环步骤 j j j 处的参数, Φ ( ⋅ ; φ i j ) Φ(·;φ^j_i) Φ(⋅;φij) 表示用这些参数对网络 Φ Φ Φ 进行评估。最后的专用参数 φ i k φ^k_i φik 现在用于对测试集 X i t e s t X^{test}_i Xitest 进行预测,并计算外环损耗 L t e s t \mathcal{L}_{test} Ltest。最后,我们通过内环更新步骤将损耗 L t e s t \mathcal{L}_{test} Ltest 反向传播到参数 θ θ θ。我们进一步发现,所提出的方法受益于Li等人[38]提出的每参数学习率的灵活性。完整的算法在 算法1 中展现。
与自动解码器框架相比,这个公式有几个优点。首先,正如我们在第4节中所演示的那样,测试时的推理速度要快一个数量级,同时在定性和定量方面都表现得相当或略好。此外,由于 MAML 也优化了推理算法,因此可以训练它从不同类型的上下文观察中推断出专门的网络。例如,我们将证明,这使得仅给定零水平集上的点的 SDF 的重建成为可能,而自动解码器框架需要代理损失形式的启发式来实现这一目标。我们的经验表明,我们优于基于池的基于集合编码器的方法,这与最近发现这些编码器欠拟合上下文的工作一致[32]。最后,基于自解码器和基于自编码器的方法都假设一个低维潜在空间,而 MAML 自然在元网络的所有参数 θ θ θ 的高维空间中进行优化。
4 Analysis
在本节中,我们首先将提出的 MetaSDF 方法应用于从 MNIST 数字中提取的 2D SDFs 的学习,然后应用于 ShapeNet 数据集中的 3D 形状。所有代码和数据集都将公开提供。
4.1 Meta-learning 2D Signed Distance Functions
研究了从 MNIST 数据集中提取的二维符号距离函数(SDFs)的不同泛化方法的性质。从每一个 MNIST 数字中,我们通过距离变换提取一个二维 SDF,使得该数字的轮廓为相应 SDF 的零水平集,如 图1 所示。根据[1],我们通过全连接神经网络直接拟合 MNIST 数字的 SDF。我们对三种可选的泛化方法进行了基准测试。首先,两种基于自动解码器的方法,其中潜在代码被解码成一个函数 Φ Φ Φ,要么像[1]那样通过连接使用条件反射,要么像[8]那样通过完全连接的超网络。其次,我们比较了条件神经过程(CNP)[6],它是置换不变集编码器的代表。
Implementation. 所有模型都实现为全连接的 RELU-MLPs,具有256个隐藏单元,没有规范化层。 Φ Φ Φ 由四层实现。CNPs 的集合编码器同样使用四层。如[8]所示,超级网络由三层实现。所提出的方法执行 5 个内部循环更新步骤,其中我们将 α α α 初始化为 1×10−1。所有模型都使用 ADAM 优化器进行优化[39],学习率为 1×10−4。
Inference with partial observations. 我们证明了我们可以训练 MetaSDF 从密集的真值样本或仅从零水平集的样本中推断连续 SDF。这是值得注意的,因为仅从零水平设定点推断 SDF 相当于解决由特定Eikonal方程定义的边值问题,参见[14]。在DeepSDF[1]中,作者还演示了从零水平设点重建测试时间,但需要用启发式方法增加损失,以确保问题是良好的。Gropp等人[14]建议明确考虑损失中的Eikonal约束。我们在完整 MNIST 训练集的 SDF 上训练所有模型,通过 64×64 真 SDF 样本的规则网格提供监督。对于 CNPs 和所提出的方法,我们分别训练两个模型,条件是(1)相同的 64×64 个ground-truth SDF 样本或(2)从零水平集采样的 512 个点的集合。然后,我们测试所有模型,从这两种不同类型的上下文的未见的 MNIST 测试集重建 sdf。图2显示了结果的定性和定量比较。所有方法都定性地成功地重构了具有密集上下文集的 sdf。在定量上,metasdf 的表现与基于自动解码器的方法在密集 SDF 值上的调节相当。两种方法的性能都比CNPs高出一个数量级。这与先前的研究一致,表明基于池的集编码器倾向于欠拟合上下文集。当仅以 zero-levels set 为条件时,基于自动解码器的方法无法重建测试 SDF。相比之下,CNPs 和 metasdf 都成功地重建了SDF,所提出的方法再次显著优于CNPs。
Inference speed. 我们比较了超网络和基于连接的方法拟合单个看不见的 2D MNIST SDF 所需的时间。即使对于这个简单的示例,这两种方法在测试时也需要大约4秒的时间来收敛于未见的 SDF 的潜在代码。相比之下,提出的基于元学习的方法在 5 个梯度下降步骤或大约 50 毫秒内推断出功能表示。
Out-of-distribution generalization. 我们研究了不同的优化方法重建分布外测试样本的能力。我们考虑了三种分布外泛化模式:第一,对训练时未观察到的 MNIST 数字进行泛化。在这里,我们训练0-5,坚持 6-9。其次,泛化到随机旋转的 MNIST sdf,我们在完整的 MNIST 训练集上进行训练。最后,泛化到从 triple-MNIST 数据集中提取的有符号距离函数[40],这是一个由三个按比例缩小的数字组成的数据集。在最后一个实验中,我们在一个由完整 MNIST 训练集和双 MNIST 数据集组成的数据集上进行训练,并在三 MNIST 数据集上进行测试。双 MNIST数据集包含与目标三 MNIST 数据集相同大小的数字。图3、4和5显示了定性结果,而表1报告了定量性能。提出的 MetaSDF 方法在此任务中远远优于所有替代方法。定性地说,它成功地生成了看不见的数字和旋转的数字,尽管在这个组合性实验中没有一种方法能够准确地重建零水平集。这表明所提出的方法对分布外样本更灵活。
Interpretation as representation learning. 以前已经观察到,学习内隐表征可以被视为表征学习的一种形式[9]。在这里,我们证实了这一观察结果,并证明了使用所提出的元学习方法找到的特殊SDF网络的权重编码了有关数字类的信息,执行了无监督分类。图6为10000个MNIST sdf测试集参数的T-SNE嵌入[41]。虽然类不是完全线性可分的,但很明显,sdf编码神经网络Φ的参数携带有关MNIST数字的类的信息。
COIN:
p a r a m n u m = ( h + 6 ) w + h w 2 + 3 param_{num} = (h+6)w + hw^2 + 3 paramnum=(h+6)w+hw2+3
SW:
p a r a m n u m = ( h + 6 ) w + h w 2 + 3 − ( s n − 1 ) h w g r o w w b a s e − ( s n − 2 ) ( s n − 1 ) 2 h w g r o w 2 param_{num} =(h+6)w + hw^2 + 3 - (s_n-1)hw_{grow}w_{base} - \frac{(s_{n}-2)(s_{n}-1)}{2}hw_{grow}^2 paramnum=(h+6)w+hw2+3−(sn−1)hwgrowwbase−2(sn−2)(sn−1)hwgrow2
SD:
p a r a m n u m = ( h + 3 ) w + h w 2 + 3 + 3 s n w param_{num} = (h+3)w + hw^2 + 3 + 3 s_n w paramnum=(h+3)w+hw2+3+3snw
SWD:
p a r a m n u m = ( h + 3 ) w + h w 2 + 3 − ( s n − 1 ) h w g r o w w b a s e − ( s n − 2 ) ( s n − 1 ) 2 h w g r o w 2 + 3 s n w param_{num} =(h+3)w + hw^2 + 3 - (s_n-1)hw_{grow}w_{base} - \frac{(s_{n}-2)(s_{n}-1)}{2}hw_{grow}^2 + 3s_nw paramnum=(h+3)w+hw2+3−(sn−1)hwgrowwbase−2(sn−2)(sn−1)hwgrow2+3snw
其中 w w w 为网络宽度, d d d 为网络深度, w b a s e w_{base} wbase 为基网络宽度, w g r o w w_{grow} wgrow 为可流化增长宽度, s n s_n sn 为可流化阶段数
COIN++: Neural Compression Across Modalities
Abstract
神经压缩算法通常基于自动编码器,需要专门的编码器和解码器架构来处理不同的数据模式。在本文中,我们提出了 COIN++,这是一个神经压缩框架,可以无缝地处理各种数据模式。我们的方法是基于将数据转换为隐式神经表示,即将坐标 (如像素位置) 映射到特征 (如RGB值) 的神经函数。然后,我们不是直接存储隐式神经表示的权重,而是将应用于元学习基础网络的调制作为数据的压缩代码存储。我们进一步对这些调制进行量化和熵编码,从而获得较大的压缩增益,同时与基线相比将编码时间减少了两个数量级。我们通过压缩各种数据模式 (从图像和音频到医疗和气候数据) 来实证证明我们方法的可行性。
1 Introduction
据估计,每天都有几个eb的数据被创建 (Domo, 2018)。该数据由各种各样的数据模式组成,每种模式都可以从压缩中受益。然而,绝大多数神经压缩工作只关注图像和视频数据 (Ma et al, 2019)。在本文中,我们介绍了一种新的神经压缩方法,称为COIN++,它适用于从图像和音频到医疗和气候数据的广泛数据模式 (见图1)。
图1:COIN++ 通过优化将各种数据模式转换为神经网络,然后将这些神经网络的参数存储为数据的压缩代码。通过简单地改变神经网络的输入和输出维度,可以压缩不同的数据模态。
大多数神经压缩算法都是基于自编码器的(Theis et al, 2017;ball等人,2018;Minnen et al, 2018;Lee et al, 2019)。编码器将图像映射到被量化和熵编码成比特流的潜在表示。然后将比特流传输到重建图像的解码器。对编码器和解码器的参数进行训练,以共同最小化重构误差或失真以及压缩码的长度或速率。为了获得良好的性能,这些算法严重依赖于专门用于图像的编码器和解码器架构 (Cheng等人,2020b;谢等,2021;邹等,2022;Wang et al, 2022)。将这些模型应用于新的数据模式需要设计新的编码器和解码器,这通常是具有挑战性的。
最近,提出了一种新的神经压缩框架,称为 COIN (隐式神经表示压缩),它绕过了对专门编码器和解码器的需求 (Dupont等人,2021a)。与直接压缩图像不同,COIN 采用神经网络将像素位置映射到图像的 RGB 值,并将该网络的量化权重存储为图像的压缩代码。虽然 Dupont 等人 (2021a) 只将 COIN 应用于图像,但它有望存储其他数据模式。事实上,将坐标 (如像素位置) 映射到特征 (如RGB值) 的神经网络,通常被称为隐式神经表征 (INR),已被用于表示带符号距离函数 (Park等人,2019)、体素网格 (Mescheder等人,2019)、3D 场景 (Sitzmann等人,2019;Mildenhall等人,2020),温度场 (Dupont等人,2021b),视频 (Li等人,2021b),音频 (Sitzmann等人,2020b) 等等。因此,将数据转换为 INR 并对其进行压缩的类似 COIN 的方法有望构建适用于各种模式的灵活神经编解码器。
在本文中,我们识别并解决了 COIN 的几个关键问题,并提出了一种适用于多种模式的压缩算法,我们称之为 COIN++。更具体地说,我们确定了 COIN 的以下问题: 1. 编码速度很慢:压缩一张图像可能需要长达 1 小时。2. 缺乏共享结构:由于每张图像都是独立压缩的,因此网络之间没有共享信息。3. 性能远远低于 (SOTA) 图像编解码器。我们通过以下方式解决这些问题:1. 使用元学习将编码时间减少两个数量级到不到一秒,而相比之下,COIN需要几分钟或几个小时。2 .学习一个编码共享结构的基本网络,并对该网络应用调制来编码实例特定信息。对调制进行量化和熵编码。虽然我们的方法在压缩和速度方面都大大超过了 COIN,但它只是部分地缩小了与 SOTA 编解码器在充分研究的模式 (如图像) 上的差距。然而,COIN++ 适用于传统方法难以使用的广泛数据模式,使其成为非标准领域神经压缩的有前途的工具。
2 Method
在本文中,我们考虑压缩可以用坐标 x ∈ X \textbf{x}\in\mathcal{X} x∈X 和特征 y ∈ Y \textbf{y}\in\mathcal{Y} y∈Y 的集合来表示的数据。例如,图像可以用 R 2 \mathbb{R}^2 R2 中的一组像素位置 x = ( x , y ) \textbf{x}=(x,y) x=(x,y) 及其对应的 RGB 值 y = ( r , g , b ) \textbf{y}=(r,g,b) y=(r,g,b) in { 0 , 1 , … , 255 } 3 \{0,1,…, 255\}^3 {0,1,…,255}3。类似地,MRI 扫描可以用 3D 空间中的一组位置 x = ( x , y , z ) \textbf{x}=(x,y,z) x=(x,y,z) 和强度值 y ∈ R + y\in\mathbb{R}^+ y∈R+ 来描述。给定单个数据点作为坐标和特征对的集合 d = { ( x i , y i ) } i = 1 n \textbf{d}=\{(x_i,y_i)\}_{i=1}^n d={(xi,yi)}i=1n (例如,图像作为 n n n 个像素位置和 RGB 值的集合),COIN 方法包括通过最小化来拟合具有参数 θ θ θ 的神经网络 f θ : X → Y f_θ:\mathcal{X}\rightarrow\mathcal{Y} fθ:X→Y 到数据点。
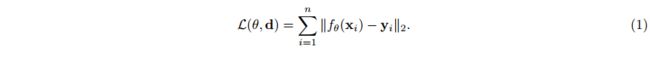
然后将权重 θ θ θ 量化并存储为数据点 d \textbf{d} d 的压缩表示。神经网络 f θ f_θ fθ 由 SIREN (Sitzmann等人,2020b) 参数化,即具有正弦激活函数的 MLP,这对于拟合高频率数据 (如自然图像) 是必要的 (Mildenhall, 2020;Tancik,2020b; Sitzmann et al.2020b)。更具体地说,SIREN 层是通过将元素 sin 应用于隐藏特征向量 h ∈ R d \textbf{h}\in\mathbb{R}^d h∈Rd 来定义的。
![]()
其中 W ∈ R d × d W\in\mathbb{R}^{d×d} W∈Rd×d 为权重矩阵, b ∈ R d \textbf{b}\in\mathbb{R}^d b∈Rd 为偏置向量, ω 0 ∈ R + ω_0\in\mathbb{R}^+ ω0∈R+ 为正比例因子。
虽然这种方法非常通用,但有几个关键问题。首先,由于压缩涉及到最小化 方程1,编码非常慢。例如,在 1080Ti GPU 上压缩来自 Kodak 数据集 (Kodak, 1991) 的单张图像需要近一个小时 (Dupont et al, 2021a)。其次,由于每个数据点 d \textbf{d} d 都是用一个单独的神经网络 f θ f_θ fθ 拟合的,所以数据点之间没有信息共享。当有几个数据点可用时,这显然是次优的:例如,自然图像共享许多公共结构,不需要为每个单独的图像重复存储。在接下来的章节中,我们将展示我们所建议的方法 COIN++ 如何在保持 COIN 通用性的同时解决这些问题。
2.1 Storing modulations
当 COIN 将每个图像存储为单独的神经网络时,我们转而训练跨数据点共享的基础网络,并对该网络应用调制来参数化单个数据点。给定一个基本网络,如多层感知器 (MLP),我们使用 FiLM 层 (Perez等人,2018),通过应用元素尺度 γ ∈ R d \gamma\in\mathbb{R}^d γ∈Rd 和位移 β ∈ R d \beta\in\mathbb{R}^d β∈Rd 来调制网络的隐藏特征 h ∈ R d \textbf{h}\in\mathbb{R}^d h∈Rd。
![]()
给定一个固定的基础 MLP,因此我们可以通过在每层应用不同的尺度和位移来参数化神经网络族。因此,每个神经网络函数都由一组尺度和移位来指定,这些尺度和移位统称为调制 (Perez et al ., 2018)。最近,FiLM 方法也被应用于 INRs 的背景下。Chan等人 (2021) 通过 SIREN 网络对生成式对抗网络中的生成器进行参数化,并通过对该网络应用 s i n ( γ ⊙ ( W h + b ) + β ) sin(\gamma\odot(W\textbf{h} +\textbf{b})+\beta) sin(γ⊙(Wh+b)+β) 的调制来生成样本。同样,Mehta等人 (2021) 通过 α ⊙ sin ( W h + b ) \alpha\odot\sin(W\textbf{h}+\textbf{b}) α⊙sin(Wh+b) 使用尺度因子参数化 INR 族。这两种方法都可以修改为使用映射到一组调制的低维潜在向量,而不是直接应用调制。Chan 等人 (2021) 使用 MLP 将潜在向量映射为缩放和移位,而 Mehta 等人 (2021) 通过与基础网络形状相同的 MLP 映射潜在向量,并使用该网络的隐藏激活作为调制。然而,我们发现这两种方法在可压缩性方面表现不佳,需要大量的调制才能实现令人满意的重建。
相反,我们提出了一种新的参数化调制的 INR,除了产生更好的压缩率,也产生更稳定的训练。更具体地说,给定一个基本的 SIREN 网络,我们只应用位移 β ∈ R d \beta\in\mathbb{R}^d β∈Rd 作为调制使用。
![]()
在 MLP 的每一层。为了进一步减少存储,我们使用一个潜在向量,它线性映射到调制,如 图2 所示。在稍微超载的符号中,我们也把这个向量称为调制或潜在调制。事实上,我们从经验上发现,只使用位移与同时使用位移和尺度具有相同的性能,而只使用尺度产生了相当差的性能。此外,将潜在向量线性映射到调制比像 Chan 等人 (2021) 那样使用深度 MLP 效果更好。给定此参数化,然后我们将数据点 d \textbf{d} d (例如图像) 存储为一组 (潜在) 调制 ϕ \phi ϕ。为了解码数据点,我们简单地对调制基网络 f θ ( ⋅ ; ϕ ) f_\theta(\cdot;\phi) fθ(⋅;ϕ) 在每个坐标 x \textbf{x} x 处。
![]()
如 图3 所示。为了拟合一组调制 ϕ \phi ϕ 到数据点 d \textbf{d} d,我们保持基本网络的参数 θ θ θ 固定并最小化下式通过 ϕ \phi ϕ。
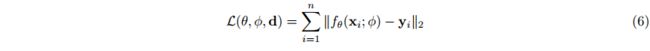
与 COIN 相比,每个数据点 d \textbf{d} d 被存储为单独的神经网络 f θ f_θ fθ, COIN++ 只需要存储 O ( k ) O(k) O(k) 个调制 (或更少,当使用潜在时),而不是 O ( k 2 ) O(k^2) O(k2) 个权重,其中 k k k 是 MLP 的宽度。此外,这种方法允许我们在基本网络中存储共享信息,在调制中存储特定于实例的信息。例如,对于自然图像,基本网络编码自然图像共有的结构,而调制存储重建单个图像所需的信息。
2.2 Meta-learning modulations
给定一个基本网络 f θ f_θ fθ,我们可以通过最小化 公式6 来编码数据点 d \textbf{d} d。然而,我们仍然面临着两个问题:1. 我们需要学习基本网络的权值 θ θ θ。2. 通过 公式6 编码一个数据点很慢,需要成千上万次的梯度下降迭代。COIN++ 用元学习解决了这两个问题。
最近,Sitzmann et al(2020a);Tancik(2020a) 已经表明,将模型不可知元学习 (MAML) (Finn等人,2017) 应用于 INR 可以将测试时的拟合减少到只有几个梯度步骤。代替从随机初始化直接通过梯度下降最小化 L ( θ , d ) \mathcal{L}(\theta, \textbf{d}) L(θ,d),我们可以元学习一个初始化 θ ∗ θ^* θ∗,使得最小化 L ( θ , d ) \mathcal{L}(\theta, \textbf{d}) L(θ,d) 可以在几个梯度步骤中完成。更具体地说,假设我们有一个 N N N 个点的数据集 { d ( j ) } j = 1 N \{d^{(j)}\}_{j=1}^N {d(j)}j=1N。从初始化 θ θ θ 开始,数据点 d ( j ) d^{(j)} d(j)上的 MAML 内部循环的一个步骤为:
![]()
其中 α α α 为内环学习率。然后,我们感兴趣的是学习一个好的初始化 θ ∗ θ^∗ θ∗,使得在整个数据点集 { d ( j ) } j = 1 N \{d^{(j)}\}_{j=1}^N {d(j)}j=1N 的几个梯度步之后,损失 L ( θ , d ) \mathcal{L}(\theta, \textbf{d}) L(θ,d) 最小。为了更新初始化 θ θ θ,我们执行外环的一个步骤,外环学习率为 β \beta β,通过:
![]()
在我们的例子中,MAML 不能直接使用,因为在测试时我们只拟合调制 ϕ \phi ϕ 而不是共享参数 θ θ θ。因此,我们需要对 θ θ θ 和 ϕ \phi ϕ 进行元学习初始化,这样,给定一个新的数据点,在保持θ不变的情况下,可以快速计算出调制 ϕ \phi ϕ。实际上,我们只存储每个数据点的调制,并在所有数据点之间共享参数 θ θ θ。对于 COIN++,内循环的一个步骤由:
![]()
θ θ θ 是固定的。Zintgraf 等人(2019)之前已经探索过对参数子集执行内循环,称为 CAVIA。正如在 CAVIA 中观察到的,元学习中 ϕ \phi ϕ 的初始化是冗余的,因为它可以被吸收到基本网络权重 θ θ θ 的偏置参数中。因此,我们只需要元学习共享参数初始化 θ θ θ。外循环的更新规则由:
![]()
然后内部循环更新调制 ϕ \phi ϕ,而外部循环更新共享参数 θ θ θ。该算法允许我们元学习一个基本网络,这样每个调制集都可以轻松快速地拟合 (见图4)。在实践中,我们发现只需 3 个梯度步骤就可以获得令人信服的结果,而对于 COIN 则需要数千个梯度步骤。
2.3 Patches, quantization and entropy coding for modulations
Patches for large scale data. 虽然元学习基础网络允许我们快速将新数据点编码为调制,但训练过程是昂贵的,因为 MAML 必须通过内环进行梯度(Finn et al, 2017)。对于大数据点(如高分辨率图像或MRI扫描),这可能会变得非常昂贵。虽然一阶近似存在(Finn等人,2017;Nichol等人,2018;Rajeswaran等人,2019),我们发现它们严重阻碍了性能。相反,为了减少内存使用,我们在训练期间将数据点分成随机的小块。例如,对于大规模图像,我们在32×32补丁上进行训练。在训练时,我们学习一个基本网络,这样调制可以很容易地适应补丁。在测试时,我们将一个新图像分成几个补丁,并为每个补丁计算调制。然后,图像由所有补丁的调制集表示 (见图4)。我们对其他数据模式使用类似的方法,例如,MRI 扫描被分割成 3D 补丁。
**Quantization. ** 虽然 COIN 将神经网络权重从 32 位量化到 16 位以减少存储空间,但超过这个量化会严重影响性能(Dupont et al, 2021a)。相反,我们发现调制是惊人的可量化的。在元学习期间,调制由 32 位浮点数表示。为了将这些量化为更短的比特宽,我们简单地使用均匀量化。我们首先对调制进行剪辑,使其位于其平均值的 3 个标准差以内。然后我们将这个区间分成 2 个大小相等的箱子(其中 b 是比特数)。值得注意的是,我们发现将比特数从 32 位减少到 5 位(即将符号数从超过 109 个减少到只有 32 个)只会导致重建精度的小幅下降。简单地应用均匀量化,然后将压缩提高 6 倍,而重建质量的成本很小。
Entropy coding. 几乎所有编解码器的核心组件都是熵编码,它允许使用算术编码对量化代码进行无损压缩 (Rissanen & Langdon, 1979)。这依赖于量子化码的分布模型。与量化一样,我们使用一种非常简单的方法来建模该分布:我们计算训练集中每个量化调制值的频率,并在测试时使用该分布进行算术编码。在我们的实验中,这在不影响重建质量的情况下减少了 8-15% 的存储。虽然这种简单的熵编码方案工作得很好,但我们希望更复杂的方法能显著提高性能,这是未来工作的一个令人兴奋的方向。
最后,我们注意到,我们只传输调制,并假设接收器可以访问共享的基础网络。因此,只有调制被量化、熵编码并计入最终压缩文件大小。这类似于典型的神经压缩设置,其中假设接收器可以访问自编码器,并且只传输量化和熵编码的潜在向量。
3 Related Work
Neural compression. 学习压缩方法通常基于自动编码器,共同最小化速率和失真,如 ball 等人(2017)最初介绍的那样;Theis et al(2017) ball(2018) 通过添加超先验来扩展这一点,而 Mentzer 等人(2018);Minnen et al (2018);Lee等人(2019) 使用自回归模型来改进熵编码。Cheng等人(2020b) 通过增加潜在代码分布的注意和高斯混合模型来提高熵模型的准确性,而 Xie 等人(2021)使用可逆卷积层来进一步提高性能。虽然其中大多数都是在传统的失真指标(如MSE或SSIM)上进行优化的,但其他工作已经探索了使用生成对抗网络来优化感知指标(Agustsson等人,2019;Mentzer et al, 2020)。神经压缩也被应用于视频(Lu et al, 2019;Goliński等,2020;Agustsson et al, 2020)和音频(Kleijn et al, 2018;Valin & Skoglund, 2019;Zeghidour et al, 2021)。
Implicit neural representations and compression. 除了COIN,最近的几项工作探索了使用 INRs 进行压缩。Davies等人(2020)用神经网络编码 3D 形状,并表明与传统的抽取网格相比,这可以减少内存使用。Chen等人(2021)通过卷积神经网络表示视频,卷积神经网络将时间指标作为输入,输出视频中的一帧。通过对该网络的权值进行剪枝、量化和熵编码,实现了接近标准视频编解码器的压缩性能。Lee等人(2021)对 INRs 进行了元学习稀疏和参数高效初始化,并表明这可以减少以给定重建质量存储图像所需的参数数量,尽管它还不能与 JPEG 等图像编解码器竞争。Lu et al.(2021);Isik等人(2021)探索了使用 INRs 进行体积压缩。Zhang等人(2021)使用 INR (量化和熵编码)压缩视频中的帧,同时学习流扭曲来模拟帧之间的差异。尽管性能仍然落后于标准视频编解码器,但视频基准测试的结果是有希望的。在并行工作中,str mpler等人(2021)提出了一种使用 INRs 进行图像压缩的方法,该方法与我们的方法密切相关。作者还对 MLP 初始化进行了元学习,随后对适合图像的 MLP 的权重进行量化和熵编码,从而获得了比 COIN 更大的性能提升。特别是,对于大规模图像,他们的方法明显优于 COIN 和 COIN++,因为它们不使用补丁。然而,他们的方法仍然需要在测试时进行数万次迭代才能完全收敛,而不像我们只需要 10 次迭代(快了三个数量级)。此外,作者没有使用调制,而是在测试时直接学习 MLP 的权重。最后,与我们的工作不同,他们的方法并不适用于广泛的模式,包括音频、医疗和气候数据。事实上,据我们所知,这些工作中没有一个考虑过 INR 来构建跨数据模式的统一压缩框架。
4 Experiments
我们在四种数据模式上评估 COIN++:图像、音频、医疗数据和气候数据。我们在 PyTorch (Paszke等人,2019) 中实现所有模型,并在单个 GPU 上进行训练。对于学习率为 1e-2 的内环,我们使用 SGD;对于学习率为 1e-6 或 3e-6 的外环,我们使用Adam。我们将坐标 x \textbf{x} x 归一化为在 [- 1,1] 内,特征 y \textbf{y} y 归一化为在 [0,1] 内。重现所有结果所需的完整实验细节可在附录中找到。我们使用压缩和真实数据之间的 MSE 来训练 COIN++。作为标准,我们使用 PSNR (以dB为单位)测量重建性能(或失真),其定义为 P S N R = − 10 log 10 ( MSE ) PSNR=−10\log_{10}(\text{MSE}) PSNR=−10log10(MSE)。我们用比特每像素 (bpp) 来衡量压缩数据的大小(或速率),这是由 number of bits number of pixels \frac{\text{number of bits}}{\text{number of pixels}} number of pixelsnumber of bits 给出的。我们根据大量基线对 COIN++ 进行基准测试,包括标准图像编解码器 JPEG (Wallace, 1992), JPEG2000 (Skodras等人,2001),BPG (Bellard, 2014)和VTM (Bross等人,2021)基于自动编码器的神经压缩- BMS (ball等人,2018),MBT (Minnen等人,2018)和CST (Cheng等人,2020b) -标准音频编解码器- MP3 (MP3, 1993) -和COIN (Dupont等人,2021a)。为了清晰起见,我们对不同的编解码器使用一致的颜色,并使用实线和虚线绘制学习编解码器和标准编解码器。重现论文中所有实验的代码可以在 https://github.com/EmilienDupont/coinpp 上找到。
4.1 Comparisons to other INR parameterizations
我们首先将我们的 INR 参数化与 Chan 等人(2021)和 Mehta 等人(2021)提出的方法进行比较,如第 2.1 节所述。如 图5 所示,我们的方法在可压缩性方面明显优于这两种方法,在参数数量相同的情况下,将 PSNR 提高了2dB。此外,使用移位调制比使用尺度和移位更有效,并且比单独使用尺度要好得多。我们还注意到,我们的方法允许我们仅使用几百个参数快速拟合 INR。这与现有的 INRs 元学习研究形成对比 (Sitzmann et al, 2020a;Tancik et al ., 2020a),通常需要在测试时拟合 3 个数量级以上的参数。
4.2 Images: CIFAR10
我们使用 128、256、384、512、768 和 1024 个潜在调制在 CIFAR10 上训练 COIN++。如 图6 所示,COIN++的性能大大优于COIN、JPEG 和 JPEG2000,同时部分缩小了与 BPG 的差距,特别是在低比特率下。据我们所知,这是第一次使用 INRs 压缩优于像 JPEG2000 这样的图像编解码器。COIN++ 和 SOTA 编解码器 (BMS, CST) 之间的部分差距可能是由于熵编码:我们使用2.3节中描述的简单方案,而 BMS 和 CST 使用深度生成模型。我们假设使用深熵编码调制将显著减少这一差距。图6 显示了我们的模型和 BPG 之间的定性比较,以突出显示使用 COIN++ 获得的压缩工件的类型。为了彻底分析和评估 COIN++ 的每个组成部分,我们进行了大量的消融研究。
Quantization bitwidth. 将调制量化到较低的位宽会以重构精度为代价产生更多的压缩代码。为了理解这两者之间的权衡,我们在图7a中显示了从3位到8位量化时的速率失真图。可以看到,最佳位宽出奇地低: 在低比特率下 5 位是最佳的,而在高比特率下 6 位是最佳的。通过量化调制获得的定性伪影如图14所示。
Quantization COIN vs COIN++. 我们在 图7b 中比较了 COIN 和 COIN++ 量化后的 PSNR 下降。可以看出,调制是非常可量化的:当直接量化 COIN 权重时,性能在 14 位左右显着下降,而量化调制即使在使用 5 位时也会产生小的 PSNR 下降。然而,如 图7c 所示,对于更大的模型,量化带来的 PSNR 下降更大。
Entropy coding. 图7d 显示了全精度、量化和熵编码调制的速率失真图。可以看出,量化和熵编码都显著提高了性能。
Encoding/decoding speed. 表1 显示了 CIFAR10 上 BPG、COIN 和 COIN++ 的平均编码和解码时间。由于 BPG 运行在 CPU 上,而 COIN 和 COIN++ 运行在GPU上,这些时间不能直接比较。然而,我们遵循文献中的标准实践,在 GPU 上运行所有神经编解码器,在 CPU 上运行标准编解码器(参见附录B.1有关硬件详细信息)。在编码方面,COIN++ 压缩图像的速度比 COIN 快 300 倍,压缩率提高 4 倍。注意,这些结果是通过分别压缩每个图像获得的。当使用批量图像时,当使用 10 个内部循环步骤时,我们可以在 4 分钟内压缩整个 CIFAR10 测试集 (10k图像) (当使用3个步骤时,只需要1分钟多一点)。此外,如附录中的 图15 所示,COIN++ 只需要 3 个梯度步骤就可以达到与 COIN 相同的性能,需要 10000 个步骤,而使用的存储空间却少了 4 倍。在解码方面,由于使用更大的共享网络和熵编码,coin++比COIN慢。然而,用coinc++解码仍然很快(大约毫秒)。
4.3 Climate data: ERA5 global temperature measurements
略
4.4 Compression with patches
为了评估第 2.3 节中的修补方法,并证明 COIN++ 可以扩展到大数据(尽管在性能上有代价),我们在图像、音频和 MRI 数据上测试了我们的模型。
Large scale images: Kodak. Kodak 数据集 (Kodak, 1991) 包含 24 张大小为 768×512 的大比例尺图像。为了训练模型,我们使用来自 Vimeo90k 数据集 (Xue et al, 2019) 的随机 32×32 补丁,该数据集包含 154k 图像,大小为 448×256。在评估时,每个柯达图像被分割成 384 个 32×32补丁,这些补丁被独立压缩。由于我们没有对图像的全局结构进行建模,因此我们预计与不需要修补的情况相比,性能会显著下降。如 图9 所示,COIN++ 的性能确实有所下降,但在低比特率下仍然优于 COIN 和 JPEG。我们期望通过对图像的全局结构进行建模 (例如,两块蓝天几乎相同,但当前设置中没有利用信息冗余),这可以大大改善,但将其留给未来的工作。
Audio: LibriSpeech. 略
Medical data: brain MRI scans. 略
5 Conclusion, limitations and future work
Conclusion. 我们介绍 COIN++,这是第一个(据我们所知)应用于广泛数据模式的神经编解码器。与 COIN 相比,我们的框架在压缩和编码时间方面显著提高了性能,同时与 JPEG 等成熟的编解码器竞争。虽然 COIN++ 的性能比不上 SOTA 编解码器,但我们希望我们的工作将有助于扩展神经压缩适用的领域范围。
Limitations. COIN++ 的主要缺点是,由于 MAML 需要二阶梯度,训练模型需要大量内存。这反过来又限制了可伸缩性,并要求我们使用补丁来处理大数据。设计有效的一阶近似或完全绕过元学习将缓解这些问题。此外,训练 COIN++ 偶尔会不稳定,尽管模型通常会从损失不稳定中恢复 (参见附录中的图12)。此外,我们的框架无法处理一些常见的模式,例如文本或表格数据,因为它们不容易表示为连续函数。最后,COIN++ 落后于 SOTA 编解码器。的确,虽然我们已经证明了与自动编码器相比,COIN++ 适用于不同模式的普遍性(因为它们不需要专门的、可能复杂的特定于模式的编码器和解码器),但目前尚不清楚 COIN++ 是否能胜过针对每种模式的自编码器。然而,我们相信未来的工作有几个有趣的方向来提高基于 INR 的编解码器的性能。
Future work. 在目前的形式中,COIN++ 使用非常基本的方法来进行量化和熵编码——在这两个步骤中使用更复杂的技术可能会带来很大的性能提升。事实上,最近在函数分布建模方面的成功(Schwarz et al, 2020;Anokhin et al, 2021;Skorokhodov等,2021;Dupont等人,2021b)建议使用深度生成模型来学习熵编码调制的分布可以获得很大的收益。同样,更好的训练后量化(Nagel等人,2019;Li et al ., 2021a)或量化感知训练(Krishnamoorthi, 2018;Esser et al, 2020)也会提高性能。更一般地说,模型压缩文献中有大量的方法可以应用于 COIN++ (Cheng et al ., 2020a;Liang et al, 2021)。对于大规模数据,对斑块的全局结构进行建模,而不是独立地对它们进行编码和熵编码,这将是一种有趣的方法。此外,inr领域正在迅速发展,这些进步也可能改善COIN++。例如,Martel等人(2021)使用自适应补丁将 INR 缩放到十亿像素的图像-这种输入分区类似于 BPG 中使用的可变大小块(Bellard, 2014)。此外,使用更好的激活函数(Ramasinghe & Lucey, 2021)来增加 PSNR 和平衡模型(Huang et al, 2021)来减少内存使用是未来研究的令人兴奋的途径。
最后,由于 COIN++ 以灵活的优化过程取代了传统神经压缩中的编码器,并以强大的函数表示取代了解码器,因此我们相信使用 INR 进行压缩具有巨大的潜力。INRs 的进步,结合更复杂的熵编码和量化,可能使类似 COIN 的算法与 SOTA 编解码器相等甚至超过 SOTA 编解码器,同时潜在地允许对当前未探索的模式进行压缩。

