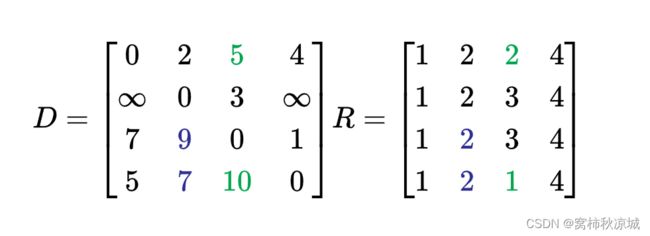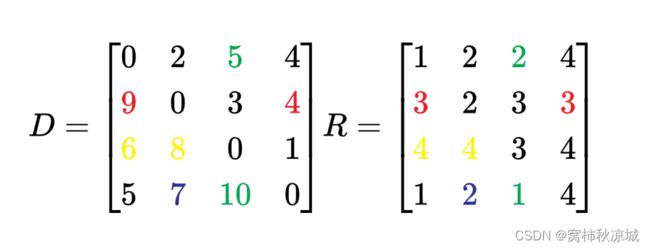从实例出发,让你一文实现Floyd算法
目录
-
-
- 看完必会的Folyd算法!
-
- 前言
- Floyd实现原理
- 从实例出发理解
-
- 概念理解一:距离矩阵
- 概念理解二:路径矩阵
- 举个例子
- 代码实现
-
看完必会的Folyd算法!
前言
最近在学习算法的过程中,接触了最短路径这一专题,又由于在数模比赛中,此算法出现的概率较为频繁,所以记下这篇,希望对大家有所帮助
Floyd实现原理
假设说,我们从A点到达B点的距离为10,但是从A先到C,再到B的距离为9,那么我们选择的路径是不是应该选择A->C->B呢,这其实就是Floyd中的最简单的实例,也就是说,我们在两个位置之间,选择一个中转点进行判断,如果,经过了中转点的路径比直接到达的路径更短,则选择具有中短点的这条线。
可能单纯的文字有些苍白,最主要的是我们通过实例进行理解!
从实例出发理解
概念理解一:距离矩阵
- 距离矩阵正如名字所说,其记录的便是两个点之间的最短距离,这个所谓的最短距离便是在不断的选取中转点来进行更新的。
- 我们假设我们选取的中转点为K,第一个点为i,第二个点为j
- 那么D(i,j)则表示的是第i个点到j个点的距离,D(i,k)表示的是第i个点到中转点K的距离
- 那么:距离矩阵更新的条件可以用下面不等式表示
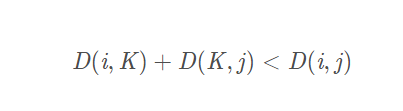
其中D(i,K)+D(K,j)表示i到j从K中转的距离,D(i,j)表示从i到j的最短距离,如果前者比后者小,那么就D(i,j)进行更新:D ( i , j ) = D ( i , K ) + D ( K , j ) ,这样就更新了距离矩阵。
那么我们该如何记录这条路线呢?
这个时候便需要用到我们的路径矩阵了!
概念理解二:路径矩阵
- 路径矩阵所表示的是,两个点之间所需要经过的中转点,假设说我们从A点到B点需要经过C点才是最短路径,那么我们可以表示为R(A,B)=C,这个时候,如果说R(C,B)=D,这个表示什么呢?说明C点到B点需要经过一个D点,如果D点到B点没有经过中转点,那么此时最短路径那显然就是A->C->D->B。
- 那么路径矩阵一开始的值是多少呢?比如R(I,J)的值应该为多少呢?对了,答案为J,因为一开始我们所认为的路径是直接从I到J点,那么不就相当于中转点就是J点了吗?
举个例子
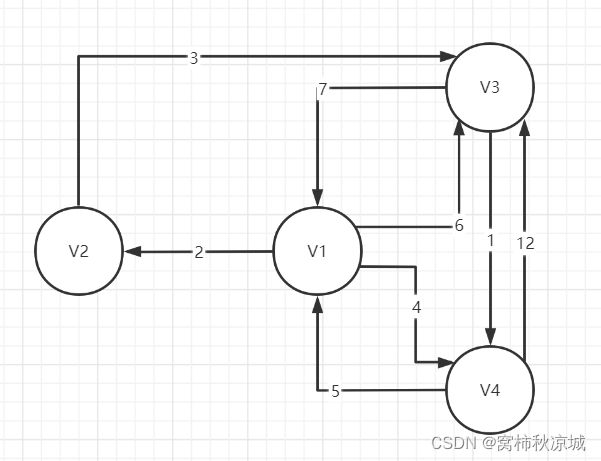
- 初始化矩阵,这里有个需要注意的点是,**如果没有从i点直接到达j点的路线,那么D(i,j)记为无穷大,例如从V2->V1没有直接的线路,所以记为无穷大。**从i到i,即从自己出发到自己,那么最短的路径自然而然的就为0了,初始化时这两点需要大家清楚。
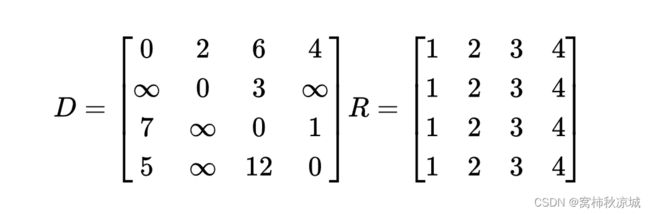
而初始化后,我们所需要做的便是遍历中转点,然后判断每个i到每个j的距离是否应该更新。
- 什么意思呢?简而言之就是三重循环,首先我们先判断第几个点作为中转点,然后在选择起始点,再选定好起始点后,再遍历终点。
- 举个例子:我们先选择第一个点作为中转点,**然后选择第一个点作为起点,那么我们选定好起点后,是不是要从第一个点遍历到最后一个点作为终点,**判断从起点(第一个点)到终点是否需要根据中转点来进行更新矩阵。
- 当第一个起点选定后,其终点从第一个点到最后一个点都遍历完后,再选择第二个点作为起点。从第一个点到最后一个点作为终点,即判断(2,1)(2,2)…的距离是否需要根据第一个中转点进行跟新
- 当起点全部选完后,我们应该再选择第二个点作为中转点,这时,我们比较的便是是通过第一个中转点更近呢还是第二个中转点更近呢,我们只要重复上面选定起点和终点的操作就行。
- 当我们三重循环下来,所得到的每两个点之间的距离便是最短了,并且与此同时我们也得到了,每两个点之间需要经过哪个中转点距离才最短。
首先由V1进行中转那么V1到到各个点的距离还是不变。
V2没有到达V1的路径,所以也就不存在从V1中转的情况,所以V2到各个点的距离还是不变。
V3可以经由V1中转,那么这个时候判断一下中转前和中转后的距离大小,将最小距离留存下来如:
V3->V1 = 7 不变
V3->V2 = inf,经由V1中转之后V3->V1->V2 = 9, 于是V3到V2的最短距离变化为9,更新路由矩阵R(3,2) = R(3,1) = 1
V3->V4 = 1,经由V1中转之后V3->V1->V4 = 11, 于是V3到V4的最短距离就还是1
同理:
V4->V2 = inf, 经由V1中转之后V4->V1->V2 = 7, 于是V4到V2的最短距离变化为7,更新路由矩阵R(4,2) = R(4,1) = 1
V4->V3 = 12,经由V1中转之后V4->V1->V3 = 11, 于是V4到V2的最短距离变化为11,更新路由矩阵R(4,3) = R(4,1) = 1
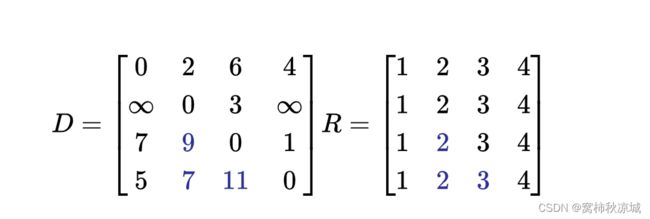
- 那么我们经过第一个中转点后,所得到的距离矩阵和路径矩阵就如下:
接下来在V1中转后的距离矩阵和路径矩阵下,来进行V2中转:
V1->V2 = 2
V1->V3 = 6,经由V2中转之后V1->V2->V3 = 5, 于是V1到V3的最短距离变化为5,更新路由矩阵R(1,3) = R(1,2) = 2
V1->V4 = 4
V2->V1 = inf
V2->V3 = 3
V2->V4 = inf
V3->V1 = 7
V3->V2 = 9
V3->V4 = 1
V4->V1 = 5
V4->V2 = 7
V4->V3 = 11,经由V2中转之后V4->V2->V3 = 10, 于是V4到V3的最短距离变化为10,更新路由矩阵R(4,3) = R(4,2) = 1。
同理,加下来进行V3中转和V4中转,由于过程类似,这里就不再赘述了,最后得到的矩阵应该是如下
这样我们就得到了最终的每两个点之间的最短距离和路线矩阵了?
- 这边给大家举个表示出路径的例子:
例如从V4->V3我们应该怎么走呢,从路径矩阵可以看到R(4,3)=1,也就是说4到3首先需要经过1作为中转点,那么加下来就是看1到3怎么走了,R(1,3)=2,从1到3需要经过2作为中转点,加下来再看2到3该怎么走,R(2,3)=3,说明2到3可以直接到达3,不需要中转
最后我们所得到的路径应该是:V4->V1->V2->V3
代码实现
我们通过代码会更好的理解算法的实现过程
% floyd.m
% 采用floyd算法计算图a中每对顶点最短路
% d是矩离矩阵
% r是路由矩阵
% a是初始化距离矩阵的值
function [d,r]=floyd(a)
n=size(a,1);
%size(a,1)所计算的是a矩阵的列数
% 初始化距离矩阵
d=a;
% 初始化路由矩阵
for i=1:n
for j=1:n
r(i,j)=j;
end
end
r;
% Floyd算法开始
for k=1:n
for i=1:n
for j=1:n
if d(i,k)+d(k,j)路径打印代码实现十分简单,主要就是判断R(i,j)是否等于j,假如不等,则先打印中转点,然后判断R(k,j)是否等于j,等于直接打印出来就行,这里可以用一个while循环来重复判断
% DisplayPath.m 打印路径函数
function DisplayPath(route, start, dest)
% 打印出任意两点之间的最短路径
% route : 路由表
% start : 起点index
% dest : 终点index
i = 1;
while 1
if(route(start, dest) ~= dest)
fprintf('V%s -> ', num2str(start));
start = route(start, dest);
else
fprintf('V%s -> ', num2str(start));
fprintf('V%s\n', num2str(dest));
break;
end
end
注意:这边的function函数都应该另外用一个m文件写,并且文件名要和函数名一样,千万不要直接写在主函数里!
本文例子参考:最短路径-Floyd算法的matlab实现.md