机器学习（13）---降维实例

---

一、人脸识别降维

1.1 查看原图

注意：无法加载fetch_lfw_people数据集的，请参考下面链接https://blog.csdn.net/m0_62881487/article/details/132797449

from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

# faces = fetch_lfw_people(min_faces_per_person=60)
# print(faces.data.shape)
faces = fetch_lfw_people(data_home = "D:\\Download\\",download_if_missing=False,min_faces_per_person=60)
X = faces.data
#print(faces.data.shape)     (1348,2914) 1348是图像的个数
#print(faces.images.shape)   (1348, 62, 47)返回数据图片个数，每个数据特征矩阵行和列


#subplots用来创建子图画布，前两个参数是说几行几列。 fig是画布，axes就是子图对象
fig, axes = plt.subplots(3,8
                         ,figsize=(8,4) #大小
                         ,subplot_kw = {"xticks":[],"yticks":[]} #不要显示坐标轴
                        )

#对axes对象进行处理
for i, ax in enumerate(axes.flat): #axes.flat后变成了一维
   ax.imshow(faces.images[i,:,:]  #索引为i的图，取出所有行和所有列，对应(1348, 62, 47)
             ,cmap="gray")
plt.show()

1.2 降维后的图像

pca = PCA(150).fit(X)
V = pca.components_
V.shape
fig, axes = plt.subplots(3,8,figsize=(8,4),subplot_kw = {"xticks":[],"yticks":[]})
for i, ax in enumerate(axes.flat):
    ax.imshow(V[i,:].reshape(62,47),cmap="gray")
plt.show()

二、迷你案例

2.1 用人脸识别看PCA降维后的信息保存量

 1. 代码块：

from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
faces = fetch_lfw_people(data_home = "D:\\Download\\",download_if_missing=False,min_faces_per_person=60)
X = faces.data
pca = PCA(150)
X_dr = pca.fit_transform(X)

X_inverse = pca.inverse_transform(X_dr)

fig, ax = plt.subplots(2,10,figsize=(10,2.5)
                       ,subplot_kw={"xticks":[],"yticks":[]}
                      )
for i in range(10):
    ax[0,i].imshow(faces.images[i,:,:],cmap="binary_r")
    ax[1,i].imshow(X_inverse[i].reshape(62,47),cmap="binary_r")
plt.show()

 2. 结论：可以明显看出，这两组数据可视化后，由降维后再通过inverse_transform转换回原维度的数据画出的图像和原数据画的图像大致相似，但原数据的图像明显更加清晰。这说明inverse_transform并没有实现数据的完全逆转。这是因为，在降维的时候，部分信息已经被舍弃了，X_dr中往往不会包含原数据100%的信息，所以在逆转的时候，即便维度升高，原数据中已经被舍弃的信息也不可能再回来了。所以，降维不是完全可逆的。

 Inverse_transform的功能，是基于X_dr中的数据进行升维，将数据重新映射到原数据所在的特征空间中，而并非恢复所有原有的数据。但同时，我们也可以看出，降维到300以后的数据，的确保留了原数据的大部分信息，所以图像看起来，才会和原数据高度相似，只是稍稍模糊罢了。

2.2 噪音过滤

 1. 降维的目的之一就是希望抛弃掉对模型带来负面影响的特征，而我们相信，带有效信息的特征的方差应该是远大于噪音的，所以相比噪音，有效的特征所带的信息应该不会在PCA过程中被大量抛弃。inverse_transform能够在不恢复原始数据的情况下，将降维后的数据返回到原本的高维空间，即是说能够实现”保证维度，但去掉方差很小特征所带的信息“。利用inverse_transform的这个性质，我们能够实现噪音过滤。

 2. 查看数据集：

from sklearn.datasets import load_digits #手写数字的数据集
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
digits = load_digits()
#print(digits.data.shape)  (1797, 64)  8行8列
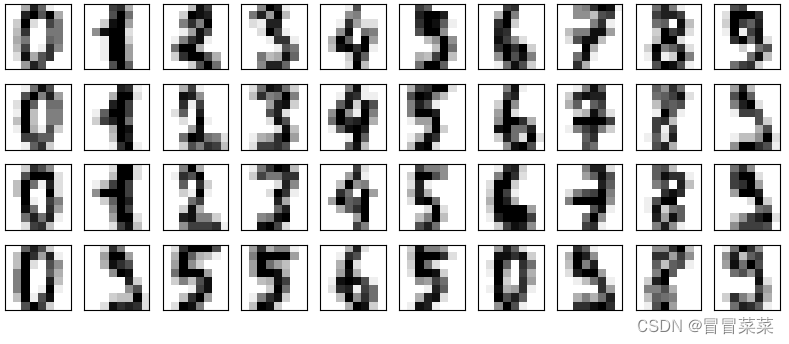
def plot_digits(data):
 fig, axes = plt.subplots(4,10,figsize=(10,4)
                          ,subplot_kw = {"xticks":[],"yticks":[]}
                         )
 for i, ax in enumerate(axes.flat):
     ax.imshow(data[i].reshape(8,8),cmap="binary")
 plt.show()
plot_digits(digits.data)

 3. 添加噪音：

np.random.RandomState(42)
#在指定的数据集中，随机抽取服从正态分布的数据
#两个参数，分别是指定的数据集，和抽取出来的正态分布的方差
noisy = np.random.normal(digits.data,2)
plot_digits(noisy)

 4. 逆转降维结果，实现降噪：

pca = PCA(0.5).fit(noisy)
X_dr = pca.transform(noisy)
without_noise = pca.inverse_transform(X_dr)
plot_digits(without_noise)

2.3 手写数字降维（随机森林）

 1. 画累计方差贡献率曲线，找最佳降维后维度的范围。

from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
data = pd.read_csv(r"D:\Download\digit recognizor.csv")
X = data.iloc[:,1:] #取除了第一列标签以外的列
y = data.iloc[:,0] #取第一列
pca_line = PCA().fit(X)
plt.figure(figsize=[20,5]) #括号里面是尺寸
plt.plot(np.cumsum(pca_line.explained_variance_ratio_))
plt.xlabel("number of components after dimension reduction")
plt.ylabel("cumulative explained variance ratio")
plt.show()

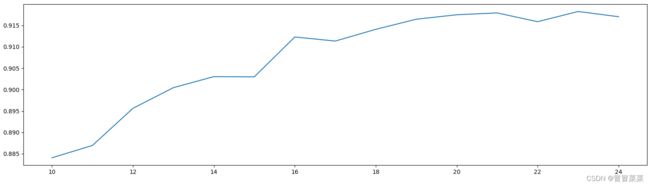
 2. 降维后维度的学习曲线，继续缩小最佳维度的范围。

score = []
for i in range(1,101,10):
    X_dr = PCA(i).fit_transform(X)
    once = cross_val_score(RFC(n_estimators=10,random_state=0)
                               ,X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(1,101,10),score)
plt.show()

 3. 细化学习曲线，找出降维后的最佳维度，从图线中可以看出最佳维度是23。

 4. 查看模型效果：

X_dr = PCA(23).fit_transform(X)
print(cross_val_score(RFC(n_estimators=100,random_state=0),X_dr,y,cv=5).mean()) #0.945

2.4 手写数字降维（KNN）

 1. 在之前的建模过程中，因为计算量太大，所以我们一直使用随机森林，但事实上，我们知道KNN的效果比随机森林更好。现在我们的特征数量已经降到不足原来的3%，可以使用KNN了。

from sklearn.neighbors import KNeighborsClassifier as KNN
print(cross_val_score(KNN(),X_dr,y,cv=5).mean()) #0.9698571428571429

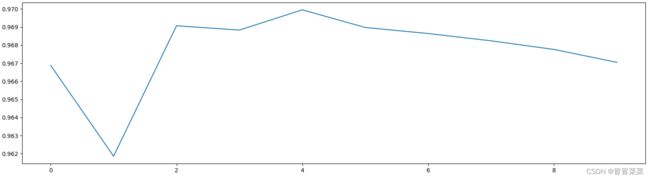
 2. KNN的k值学习曲线：KNN中参数填4时效果最好。

score = []
for i in range(10):
    once = cross_val_score(KNN(i+1),X_dr,y,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(range(10),score)
plt.show()

2.4 案例总结