【数据结构】第三章栈和队列:栈的基本概念、顺序存储实现、链式存储实现
目录
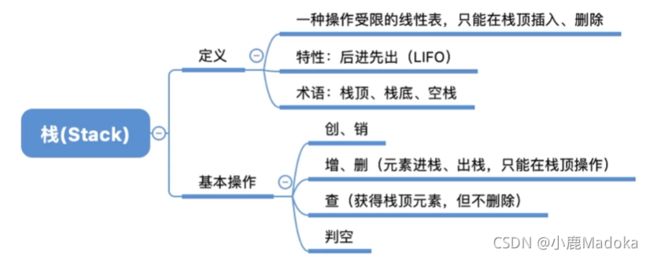
3.1_1 栈的基本概念
一、栈的定义
二、栈的基本操作
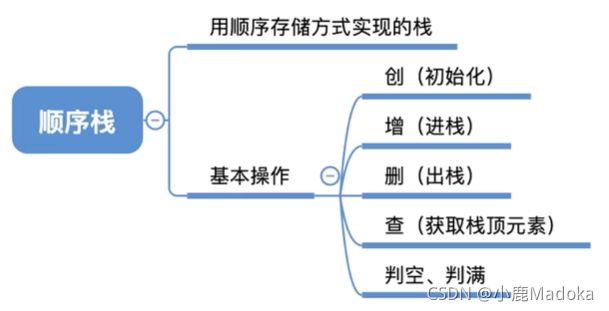
3.1_2 栈的顺序存储实现
一、顺序栈的定义、初始化、判空
二、进栈操作
三、出栈操作
四、读栈顶操作
第一种方法的完整代码(top指针指向当前栈顶元素)
五、另一种实现方式(top指针指向栈顶元素的下一个位置)
六、销毁栈
3.1_3 栈的链式存储实现
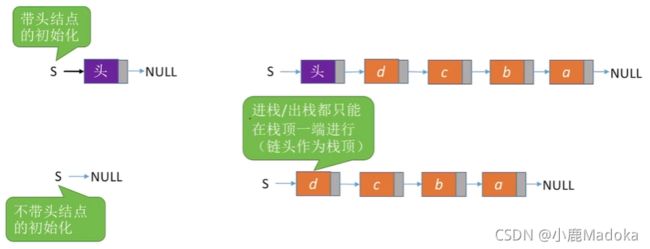
一、链栈的定义
二、链栈的代码实现(带头结点的单链表,头插头删)
3.1_1 栈的基本概念
一、栈的定义
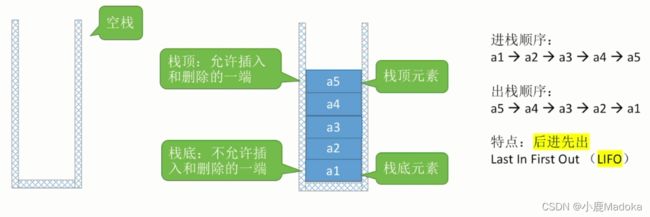
栈(Stack)是只允许在一端进行插入或删除操作的线性表。
栈的逻辑结构与普通线性表相同,但是在插入、删除上会有区别。
特点:后进先出 Last In First Out(LIFO)
重要术语:
栈顶:允许插入和删除的一段;
栈底:不允许插入和删除的一段;
空栈:没有数据元素的栈;
二、栈的基本操作
| InitStack(&S) |
初始化栈 |
构造一个空栈S,分配内存空间; |
| DestroyStack(&S) |
销毁栈 |
销毁并释放栈S所占的内存空间; |
| Push(&S, x) |
进栈 |
若S未满,则将x加入使之成为新栈顶; |
| Pop(&S, &x) |
出栈(删除栈顶元素) |
若栈S非空,则弹出栈顶元素,并用x返回; |
| GetTop(S, &x) |
读栈顶元素(不删除栈顶元素) |
若栈S非空,则用x返回栈顶元素; |
| StackEmpty(S) |
判断一个栈S是否为空 |
若S为空,则返回true,否则返回false; |
关于查找操作,栈的使用场景中大多只访问栈顶元素,所以用GetTop(S, &x)读取栈顶元素就可以了。
常考题型:
Q:分别有五个数据元素a, b, c, d, e,它们的进栈顺序也是如此,问有哪些合法的出栈顺序?
A:思路:元素不是一口气全都进栈的,所以不只有e, d, c, b, a,这一种出栈顺序;它也可以先a, b,进栈,再b, a,出栈,然后再c, d, e,的进栈、出栈,所以出栈顺序有很多,就不一一列举了;那么合法的出栈顺序一共有多少种呢?
n个不同元素进栈,出栈元素不同排列的个数为{1/(n+1)}C(下2n上n)。上述公式称为卡特兰(Catalan)数,可采用数学归纳法证明(不要求掌握)。
{1/(5+1)}C(下5上10) = (10 * 9 * 8 * 7 * 6)/(6 * 5 * 4 * 3 * 2 * 1) = 42
3.1_2 栈的顺序存储实现
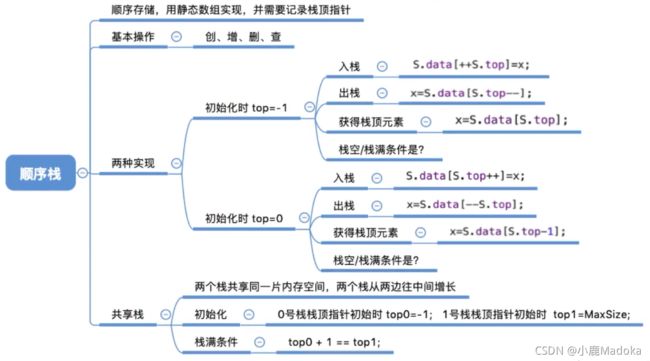
顺序栈的实现有两种方式,区别在于top指针的位置,top指针读起来有“指针”两个字,但是它是int整型变量,存放的是栈顶的位置;
第一种方法:top指针指向栈顶元素,初始化时top = -1,打个比方理解的更容易一点,就是指向了羽毛球筒里的第一个要被拿出来的羽毛球(已存在元素)的位置;
第二种方法:top指向栈顶元素的下一位,初始化时top = 0,再用相同的场景,就是指向羽毛球筒里下一个羽毛球要被放入的位置;
一、顺序栈的定义、初始化、判空
顺序栈的存储方式为顺序存储:给数据元素分配连续的存储空间,大小为:MaxSize * sizeof(ElemType);
初始化顺序栈需要注意的是:栈顶指针top是初始化为 -1 的,指针指的是当前可插入位置的前一位;
栈顶指针指向的是最上面那个元素的位置。
// 顺序栈的定义
#define MaxSize 10 // 定义栈中元素的最大个数
typedef int ElemType; // 定义顺序栈中存储的数据元素为int整型
typedef struct{
ElemType data[MaxSize]; // 静态数组存放栈元素
int top; // 栈顶指针
}SqStack; // Sq:sequence 顺序
// 初始化顺序栈
void InitStack(SqStack &S){
S.top = -1; // 初始化栈顶指针
}
// 判断栈空
bool StackEmpty(SqStack S){
if(S.top == -1){ // 栈空
return true;
}else{ // 不空
return false;
}
}
void testStack(){
SqStack S; // 声明一个栈(分配空间)
InitStack(S);
// 后续操作...
}
二、进栈操作
// 新元素入顺序栈
bool Push(SqStack &S, ElemType x){
if(S.top == MaxSize-1){ // 栈满,报错
return false;
}
S.top = S.top + 1; // 先移动栈顶指针到增加元素的位置上
S.data[S.top] = x; // 新元素入栈
// // 上面两句可以合并成下面一句
// S.data[++S.top] = x;
return true;
}
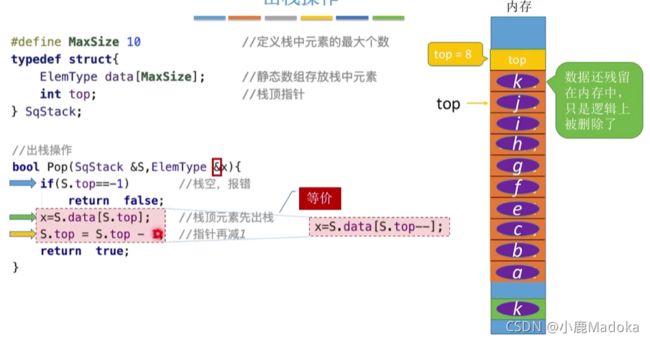
三、出栈操作
// 出栈操作
bool Pop(SqStack &S, ElemType &x){ // 因为要将出栈元素写入实参x,所以使用引用&
if(S.top == -1){ // 栈空,报错
return false;
}
x = S.data[S.top]; // 栈顶元素先取出(top指针指向的就是栈顶的那一个元素)
S.top = S.top - 1; // 栈顶指针减一,出栈
// 以上两句可以合并成下面一句
//x = S.data[S.top--];
return true;
}
四、读栈顶操作
和出栈操作很相像,不同的地方在于读栈顶元素不需要移动top指针。
// 读栈顶元素
bool GetTop(SqStack S, ElemType &x){
if(S.top == -1){ // 栈空,报错
return false;
}
x = S.data[S.top]; // x记录栈顶元素
return true;
}
第一种方法的完整代码(top指针指向当前栈顶元素)
// 20211029 顺序栈的定义及基本操作
#include
#include
using namespace std;
// 顺序栈的定义
#define MaxSize 5 // 定义栈中元素的最大个数
typedef int ElemType; // 定义顺序栈中存储的数据元素为int整型
typedef struct{
ElemType data[MaxSize]; // 静态数组存放栈元素
int top; // 栈顶指针
}SqStack; // Sq:sequence 顺序
// 初始化顺序栈
void InitStack(SqStack &S){
S.top = -1; // 初始化栈顶指针
}
// 判断栈空
bool StackEmpty(SqStack S){
if(S.top == -1){ // 栈空
return true;
}else{ // 不空
return false;
}
}
// 新元素入顺序栈
bool Push(SqStack &S, ElemType x){
if(S.top == MaxSize-1){ // 栈满,报错
return false;
}
S.top = S.top + 1; // 先移动栈顶指针到增加元素的位置上
S.data[S.top] = x; // 新元素入栈
// // 上面两句可以合并成下面一句
// S.data[++S.top] = x;
return true;
}
// 出栈操作
bool Pop(SqStack &S, ElemType &x){ // 因为要将出栈元素写入实参x,所以使用引用&
if(S.top == -1){ // 栈空,报错
return false;
}
x = S.data[S.top]; // 栈顶元素先出栈(top指针指向的就是栈顶的那一个元素)
S.top = S.top - 1; // 栈顶指针减一
// // 以上两句可以合并成下面一句
// x = S.data[S.top--];
return true;
}
// 读栈顶元素
bool GetTop(SqStack S, ElemType &x){
if(S.top == -1){ // 栈空,报错
return false;
}
x = S.data[S.top]; // x记录栈顶元素
return true;
}
int main(){
// 声明一个顺序栈(分配空间)
SqStack S;
// 顺序栈的初始化
InitStack(S);
// MaxSize 个元素入栈
ElemType data;
for(int i = 0; i < MaxSize; i++){
scanf("%d", &data);
Push(S, data);
}
printf("top栈顶指针位置%d\n", S.top);
printf("判断栈是否为StackEmpty(S)空%d\n", StackEmpty(S)) ;
// while 输出
// 顺序栈元素弹出并输出
printf("while 输出\n");
while(!StackEmpty(S)){ // 当该栈不为空时
if(GetTop(S, data)){ // 获取栈顶元素保存在data变量
printf("%3d", data);
}
Pop(S, data); // 出栈
}
// // for循环输出
// printf("for 输出\n");
// for(int i = 0; i < MaxSize; i++){
// GetTop(S, data);
// printf("%3d", data);
// Pop(S, data);
// }
return 0;
}
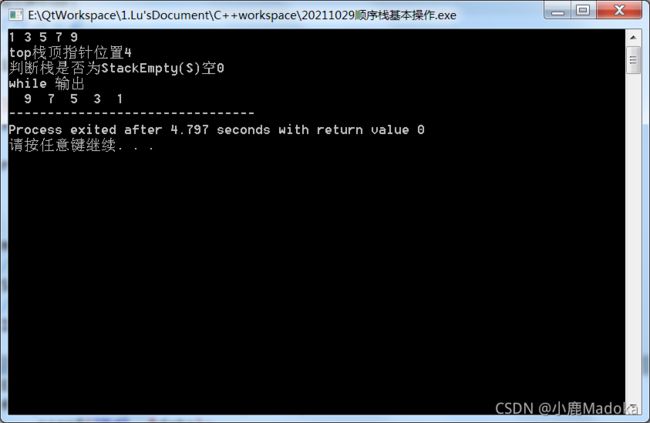
运行结果:
输入:1 3 5 7 9
五、另一种实现方式(top指针指向栈顶元素的下一个位置)
这种方式写的顺序栈,顺序栈初始化时栈顶指针top指向的是0,在判满,判空,读栈顶元素时都需要注意,和上钟方法的判断条件是不一样的;入栈、出栈的指针移动次序也不一样,写的时候也需要注意。
// 20211029 顺序栈(头结点指向下一个进栈位置)
#include
#include
using namespace std;
// 顺序栈的定义
#define MaxSize 5 // 定义栈中元素的最大个数
typedef int ElemType; // 定义栈中存的数据类型为int整型
typedef struct{
ElemType data[MaxSize]; // 静态数组中存放栈元素
int top; // 栈顶指针
}SqStack;
// 初始化顺序栈
void InitStack(SqStack &S){
S.top = 0; // 初始化栈顶指针为0,指向的是下一个要进栈的元素的位置
}
// 判断栈空
bool StackEmpty(SqStack S){
if(S.top == 0){
return true; // 栈空
}else{
return false; // 栈非空
}
}
// 入栈
bool Push(SqStack &S, ElemType x){
if(S.top == MaxSize){ // 栈满,报错
return false;
}
S.data[S.top] = x; // 新元素进栈
S.top = S.top + 1; //移动栈顶元素指向下一个进栈位置
// // 以上两句可以合并成下一句
// S.data[S.top++] = x;
return true;
}
// 出栈
bool Pop(SqStack &S, ElemType &x){
if(S.top == 0){ // 栈空,报错
return false;
}
S.top = S.top - 1; // 栈顶指针减一之后指向出栈元素
x = S.data[S.top]; // 栈顶元素先出栈
// // 以上两句可以合并成下一句
// x = S.data[--S.top];
return true;
}
// 读栈顶元素
bool GetTop(SqStack S, ElemType &x){
if(S.top == 0){ // 栈空,报错
return false;
}
x = S.data[S.top-1]; // 将栈顶元素保存在x变量中
return true;
}
int main(){
// 声明一个顺序栈
SqStack S;
// 顺序栈的初始化
InitStack(S);
// MaxSize个元素入栈
ElemType data;
for(int i = 0; i < MaxSize; i++){
scanf("%d", &data);
Push(S, data);
}
printf("top栈顶指针位置%d\n", S.top);
printf("判断栈是否为StackEmpty空栈%d\n", StackEmpty(S));
// while输出顺序栈所有元素,输出一个弹出一个
while(!StackEmpty(S)){
if(GetTop(S, data)){ // 当该栈不为空时读栈顶元素
printf("%3d", data);
}
Pop(S, data); // 出栈
}
return 0;
}
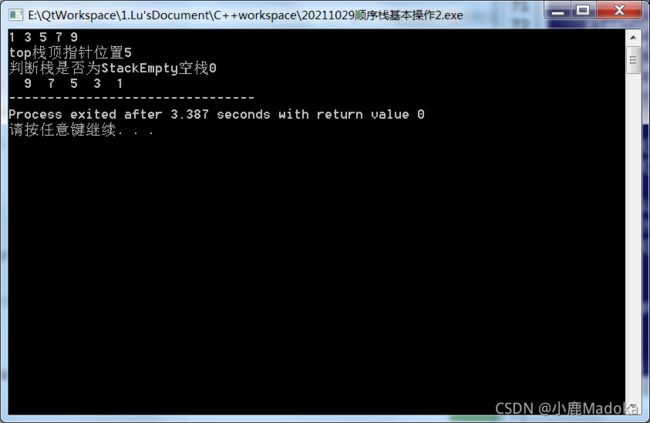
运行结果:
输入数据: 1 3 5 7 9
Q:顺序栈有一个缺点,由于是存在数组里的,一旦被定义,栈的大小就不可变了。那么如何解决栈的大小不可变这个问题?
A:用链栈或者共享栈,下面是共享栈的定义与初始化,一片空间内两个栈顶的双向奔赴。
六、销毁栈
销毁栈就是把改为-1或0(具体是多少需要看初始化栈时给它赋的数字),也就是
top = -1;
但是不必如此,因为声明栈时分配内存在栈区里,随着函数运行结束,系统自动回收内存,也就达到了清空回收的目的。
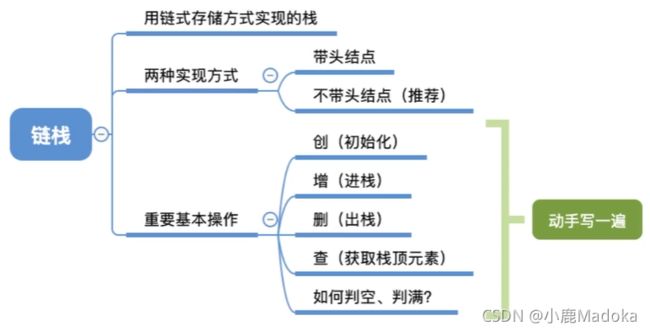
3.1_3 栈的链式存储实现
单链表对头结点的“后插”操作,与“前删”操作;
一、链栈的定义
typedef struct Linknode{
ElemType data; // 数据域
struct Linknode *next; // 指针域
}*LiStack; // 栈类型定义
具体的实现类似于单链表的前插前删,课本上不推荐带头结点“这里规定链栈没有头结点,Lhead(头指针)指向栈顶元素”(然而本人实现的并不是这一种),具体可参照 第二章线性表:单链表 有时间把这一部分代码补完。
二、链栈的代码实现(带头结点的单链表,头插头删)
没有实现不带头结点的_(:з」∠)_,我觉得带一个头结点比较好,带头结点就可以把头结点数据域存放链栈有效结点长度,以下代码为带头结点的单链表。
// 20220402 补充代码
// 3.1_3 栈的链式存储实现——带头结点的单链表(头插尾删)
#include
#include
using namespace std;
#define ElemType int
#define MaxSize 5
typedef struct Linknode{
ElemType data; // 数据域
struct Linknode *next; // 指针域
}Linknode, *LiStack; // 栈类型定义
// 初始化
bool InitStack(LiStack &L){
L = (Linknode *)malloc(sizeof(Linknode));
L->next = NULL; // 头指针初始化
L->data = 0; // 存放栈元素个数
return true;
}
// 判断栈是否为空
bool StackEmpty(LiStack L){
return (NULL == L->next);
}
// 入栈
bool Push(LiStack &L, ElemType x){
if(L->data == MaxSize) return false; // 栈满
L->data++; // 栈长度增一
// 在栈指针L的后面填一个新的结点
Linknode *s = (Linknode *)malloc(sizeof(Linknode));
s->data = x;
s->next = L->next;
L->next = s;
return true;
}
// 出栈
bool Pop(LiStack &L, ElemType &x){
if(L->data == 0) return false; // 栈空
x = L->next->data;
L->data--; // 栈长度减一
Linknode *s = L->next;
L->next = L->next->next;
free(s);
return true;
}
// 读取栈顶元素
bool GetTop(LiStack L, ElemType &x){
if(L->data == 0) return false; // 栈空
x = L->next->data;
return true;
}
// 销毁栈
bool Destroy(LiStack &L){
int num;
while(L->next != NULL){
Pop(L, num);
}
free(L);
L = NULL;
return true;
}
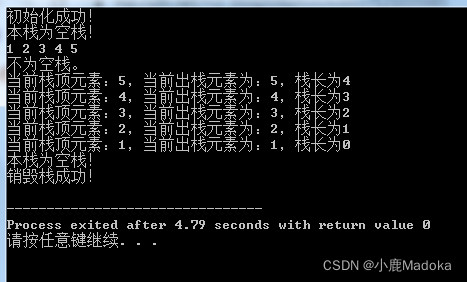
int main(){
// 声明一个指向链栈的指针
LiStack L;
int num;
// 初始化链栈
bool InitFlag = 0;
InitFlag = InitStack(L);
if(InitFlag) cout << "初始化成功!" << endl;
else cout << "初始化失败。" << endl;
// 判空
bool EmptyFlag = 0;
EmptyFlag = StackEmpty(L);
if(EmptyFlag) cout << "本栈为空栈!" << endl;
else cout << "不为空栈。" << endl;
// 入栈
for(int i = 1; i <= MaxSize; i++){
cin >> num;
Push(L, num);
}
// 判空
EmptyFlag = 0;
EmptyFlag = StackEmpty(L);
if(EmptyFlag) cout << "本栈为空栈!" << endl;
else cout << "不为空栈。" << endl;
// 出栈
for(int i = 1; i <= MaxSize; i++){
GetTop(L, num);
cout << "当前栈顶元素:" << num;
Pop(L, num);
cout <<",当前出栈元素为:" << num << ",栈长为" << L->data << endl;
}
// 判空
EmptyFlag = 0;
EmptyFlag = StackEmpty(L);
if(EmptyFlag) cout << "本栈为空栈!" << endl;
else cout << "不为空栈。" << endl;
// 销毁栈
bool DestroyFlag = 0;
DestroyFlag = Destroy(L);
if(Destroy) cout << "销毁栈成功!" << endl;
else cout << "销毁栈失败。" << endl;
return 0;
}