刷刷刷——双指针算法
双指针算法
这里的双指针，可能并不是真正意义上的指针，而是模拟指针移动的过程。
常见的有两种：
双指针对撞：
-
即在顺序结构中，指针从两端向中间移动，然后逐渐逼近
-
终止条件一般是：
left == right指向同一个位置or
left>right指针错开
快慢指针：
- 该方法一般用于处理环形链表或者是数组
283. 移动零
算法原理
这里有两种方法：
-
方法1： 开辟一个新的空间，如果不是0，而增添到新的空间，最后在补齐0即可
-
方法2：采用前后指针，
cur遍历数组，prev指向最后一个非0元素（我们采用该解法）
代码实现
class Solution {
public:
void moveZeroes(vector<int>& nums)
{
int prev = -1;
for(int cur=0; cur<nums.size();cur++)
{
if(nums[cur] != 0)
{
swap(nums[++prev],nums[cur]);
}
}
}
};
1089. 复写零
算法原理
2种方法：
-
方法1：开辟一个容量与参数一样的新的空间，遇到0就写2次，直到空间与满为止
-
方法2：找到最后一个复写的数（判断
cur的值，决定dest是走一步还是走两步）然后再从后往前遍历（从前往后遍历会导致后面的数被修改），完成复写操作这里要注意处理边界情况
代码实现
“异地操作”
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
vector<int> tmp;
tmp.resize(arr.size());
int cur = 0;
int prev = 0;
while(cur<arr.size())
{
if(prev<arr.size() && arr[cur] == 0)
{
tmp[prev++] = arr[cur];
}
if(prev<arr.size())
{
tmp[prev++] = arr[cur];
}
else
break;
++cur;
}
arr = tmp;
}
};
“本地操作”
class Solution
{
public:
void duplicateZeros(vector<int>& arr)
{
int cur = 0;
int dest = -1;
//找最后一个复写的数
while (cur < arr.size())
{
if (arr[cur] == 0)
{
dest += 2;
}
else
{
dest++;
}
if(dest >= arr.size() - 1)
{
//边界处理
if(dest == arr.size())
{
arr[arr.size() - 1] = 0;
cur--;
dest -= 2;
}
break;
}
cur++;
}
//从后往前
while (cur >= 0)
{
if (arr[cur] == 0)
arr [dest--] = arr[cur];
arr [dest--] = arr[cur];
cur--;
}
}
};
202. 快乐数
算法原理
这题可以理解为类似链表带环问题，采用“快慢指针”的方法来解决
这里的“快慢指针”是计算数据的跨度，一个每次计算平方，一个每次计算平方的平方（题目已经告诉我们，要么变成1，要么无限循环，当它循环相遇的时候不是1，那么就肯定不是快乐数）
鸽巢原理：
n个巢穴，有n+1个鸽子，那么至少有一个巢穴里面的鸽子数量大于1
以
int的最大值为例：
代码实现
class Solution
{
public:
int fastQSum(int n)
{
int tmp = 0;
int sum = 0;
while(n)
{
tmp = pow((n%10),2)+tmp;
n=n/10;
}
while(tmp)
{
sum = pow((tmp%10),2)+sum;
tmp = tmp/10;
}
return sum;
}
int slowQSum(int n)
{
int sum = 0;
while(n)
{
sum = pow((n%10),2)+sum;
n=n/10;
}
return sum;
}
bool isHappy(int n)
{
int slow = slowQSum(n);
int fast = fastQSum(n);
while(1)
{
if(fast == 1 || slow == 1)
return true;
else if(slow == fast && slow!=1)
return false;
slow = slowQSum(slow);
fast = fastQSum(fast);
}
}
};
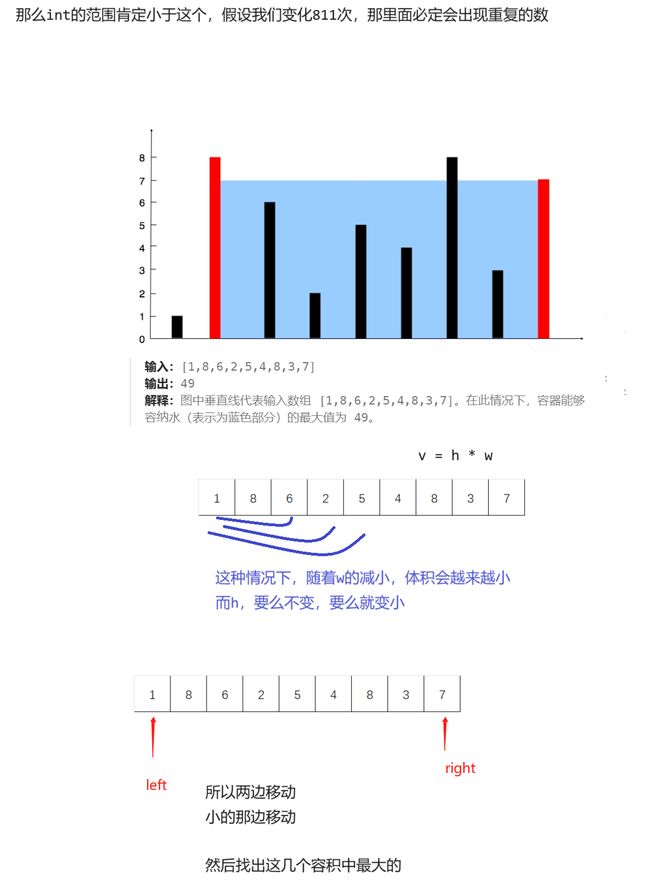
11. 盛最多水的容器
算法原理
这里可以采用暴力枚举的方法，将全部的容积算出来，但这里太暴力的，而且可能会超时
所以利用单调性，采用双指针的方法：
代码实现
class Solution {
public:
int maxArea(vector<int>& height)
{
int left = 0;
int right = height.size()-1;
int Max = 0;
while(left<right)
{
int h = min(height[left],height[right]);
int w = right-left;
int v = h*w;
if(v>Max)
{
Max = v;
}
if(height[left]<height[right])
left++;
else
right--;
}
return Max;
}
};
611. 有效三角形的个数
算法原理
三角形判断：2个较小数大于最大数，只需判断一次
这题也可以采用暴力枚举的方法，如果将这个暴力解法采用双指针优化一下，就可以降低一个量级的复杂度
- 先排序
- 固定最大数
- 在最大数的左区间，找出符合的元素
代码实现
class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(),nums.end());
int m = nums.size()-1;
int ret = 0;
while(m>=2)
{
int Max = nums[m];
int left = 0;
int right = m-1;
while(left<right)
{
int sum = nums[left]+nums[right];
if(sum>Max)
{
ret += (right-left);
right--;
}
else
{
left++;
}
}
m--;
}
return ret;
}
};
剑指 Offer 57. 和为s的两个数字
这题较简单，直接看代码：
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target)
{
int left = 0;
int right = nums.size()-1;
while(left<right)
{
int sum = nums[left]+nums[right];
if(sum == target)
{
break;
}
else if(sum>target)
{
right--;
}
else if(sum<target)
{
left++;
}
}
return {nums[left],nums[right]};
}
};
15. 三数之和
算法原理
这里最暴力的方法就是先将元素排序，然后在暴力枚举，将结果放入set去重，但这个只能在比赛或者考试的时候勉强通过，实际还是不建议这样解；
我们还是采用双指针的方法：
- 先将数组排序
- 然后固定一个数（最左、最右都可以）
- 该数的后面/前面区间，找到和为
-sum的数即可细节：
去重操作，找到结果之后，双指针跳过重复的元素；固定值也要跳过重复的元素
代码实现
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
//先排序
sort(nums.begin(),nums.end());
vector<vector<int>> ret;
int n = nums.size();
int iMin = 0;
while(iMin<n)
{
if(nums[iMin]>0)
break;
int left = iMin+1;
int right = n-1;
while(left<right)
{
int sum = nums[left]+nums[right];
int target = -nums[iMin];
if(sum == target)
{
ret.push_back({nums[iMin],nums[left],nums[right]});
left++;
right--;
//去重
while(left<right && nums[left] ==nums[left-1])
left++;
while(left<right && nums[right] ==nums[right+1])
right--;
}
else if(sum>target)
right--;
else if(sum<target)
left++;
}
iMin++;
//去重
while(iMin<n && nums[iMin]== nums[iMin-1])
iMin++;
}
return ret;
}
};
18. 四数之和
原理和三数之和一样，但这里要多一次去重操作；另外，这里的测试用例有溢出值，所以部分位置采用long long类型
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target)
{
vector<vector<int>> ret;
sort(nums.begin(),nums.end());
int n = nums.size();
int iMin = 0;
while(iMin<n)
{
//固定值
int left = iMin+1;
int right = n-1;
while(left<right)
{
int t = target-nums[iMin];
int _left = left+1;
int _right = right;
while(_left<_right)
{
int sum = nums[_left]+nums[_right];
long long _t = (long long)t-nums[left];
if(sum == _t)
{
ret.push_back({nums[iMin],nums[left],nums[_left],nums[_right]});
_left++;
_right--;
while(_left<_right && nums[_left] == nums[_left-1])
_left++;
while(_left<_right && nums[_right] == nums[_right+1])
_right--;
}
else if(sum<_t)
_left++;
else if(sum>_t)
_right--;
}
left++;
while(left<right && nums[left] == nums[left-1])
left++;
}
iMin++;
while(iMin<n && nums[iMin] == nums[iMin-1])
iMin++;
}
return ret;
}
};
}
else if(sum<_t)
_left++;
else if(sum>_t)
_right--;
}
left++;
while(left};