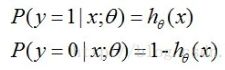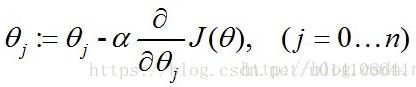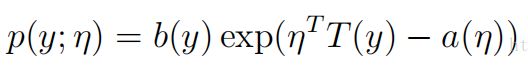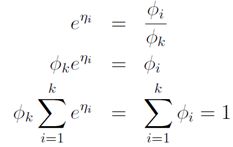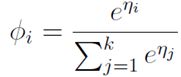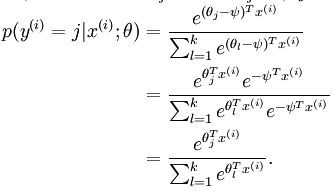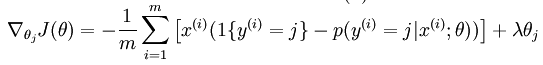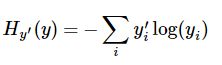深度学习2--tensorflow--Softmax回归实现手写数字识别

使用Softmax回归来实现手写数字识别，即给定一张手写数字，判断属于0--9中哪一个数字。

1.LR逻辑回归

先准备一下LR逻辑回归：

广义线性模型：实现x到y的非线性映射：

在LR逻辑回归中取g函数：实现0--1映射  输出值为  预测结果为1的概率

线性模型wx+b:

令h（x）表示结果为1的概率：

极大对数似然：

损失函数：

随机梯度下降：

2.Softmax回归

softmax属于多分类问题，多分类问题符合多项分布。可用于解决多分类问题，像决策树、朴素贝叶斯等。

首先证明多项分布属于指数分布族，这样就可以使用广义线性模型来拟合这个多项分布，由广义线性模型推导出的目标函数即为Softmax回归的分类模型。

2.1指数分布族：

η被称为分布的自然参数（也称为规范参数）；T(y)是充分统计量（对于我们所考虑的分布，通常情况下有T(y)=y）；a(η)被称为对数划分函数。这一项本质上是起到了正则化常数的作用，确保了分布p(y;η)的总和或是积分在y到1上。

2.2证明多项分布属于指数分布族

多分类模型的输出结果为该样本属于k个类别的概率，从这k个概率中我们选择最优的概率对应的类别（通常选概率最大的类别），作为该样本的预测类别。这k个概率用k个变量，…，表示。这个k变量和为1，即满足：

可以用前k-1个变量来表示，即：

使用广义线性模型拟合这个多分类问题，首先要验证这个多项分布是否符合一个指数分布族。定义T(y)为：

在这里，统计分量T(y)并没有像之前那样定义为T(y)=y，因为T(y)不是一个数值，而是一个k-1维的向量。使用符号表示向量T(y)的第i个元素。在这里引入一个新符号：，如果括号内为true则这个符号取1，反之取0，即，。所以，T(y)与y的关系就可以表示为

与关系为：

即：

多项分布表达式转化为指数分布族表达式过程如下：

其中：

变换过程：

第一步：取值为，…，中的一个，取决于y的取值。当y=i时，这一步可以理解为

第二步：消去

第三步：根据

第四、五步：转换为广义线性模型的表达格式。

2.3softmax函数表达式推导

 多项分布表达式可以表示为指数分布族表达式的格式，所以它属于指数分布族，那么就可以用广义线性模型来拟合这个多项式分布模型。

由η表达式可得：

这是关于的表达式，把它转化为关于的表达式过程为：

为了方便，令，那么

因为：

所以：

这个关于的的函数称为Softmax函数（Softmax Function）

2.4Softmax回归以及求解：

训练集       x0=1对应学习模型的截距   

将x分类为j的概率为：

令h（x）:

代价函数：

梯度下降求解：

Softmax 回归有一个特点：它有一个“冗余”的参数集。如果参数  是代价函数  的极小值点，那么  同样也是它的极小值点，其中  可以为任意向量。因此使  最小化的解不是唯一的。

证明如下：

权重衰减：

权重衰减项以后 ()，代价函数就变成了严格的凸函数，这样就可以保证得到唯一的解。 此时的 Hessian矩阵变为可逆矩阵，并且因为是凸函数，梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。

梯度下降公式：

3.tensorflow实现softmax回归

手写字体数据集的加载：

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

从MNIST_data目录下加载训练集，如果不存在则下载训练集。

读取数据集代码如下：

最终返回数据集格式：

data_sets.train	55000 组 图片和标签, 用于训练
data_sets.validation	5000 组 图片和标签, 用于迭代验证训练的准确性
data_sets.test	10000 组 图片和标签, 用于最终测试训练的准确性

def read_data_sets(train_dir, fake_data=False, one_hot=False):
  class DataSets(object):
    #python里pass用来占位
    pass
  data_sets = DataSets()
  if fake_data:
    data_sets.train = DataSet([], [], fake_data=True)
    data_sets.validation = DataSet([], [], fake_data=True)
    data_sets.test = DataSet([], [], fake_data=True)
    return data_sets
  TRAIN_IMAGES = 'train-images-idx3-ubyte.gz'
  TRAIN_LABELS = 'train-labels-idx1-ubyte.gz'
  TEST_IMAGES = 't10k-images-idx3-ubyte.gz'
  TEST_LABELS = 't10k-labels-idx1-ubyte.gz'
  VALIDATION_SIZE = 5000
  local_file = maybe_download(TRAIN_IMAGES, train_dir)
  train_images = extract_images(local_file)
  local_file = maybe_download(TRAIN_LABELS, train_dir)
  train_labels = extract_labels(local_file, one_hot=one_hot)
  local_file = maybe_download(TEST_IMAGES, train_dir)
  test_images = extract_images(local_file)
  local_file = maybe_download(TEST_LABELS, train_dir)
  test_labels = extract_labels(local_file, one_hot=one_hot)
  validation_images = train_images[:VALIDATION_SIZE]
  validation_labels = train_labels[:VALIDATION_SIZE]
  train_images = train_images[VALIDATION_SIZE:]
  train_labels = train_labels[VALIDATION_SIZE:]
  data_sets.train = DataSet(train_images, train_labels)
  data_sets.validation = DataSet(validation_images, validation_labels)
  data_sets.test = DataSet(test_images, test_labels)
  return data_sets

从指定目录下寻找数据集，如果不存在则下载：

def maybe_download(filename, work_directory):
  """Download the data from Yann's website, unless it's already here."""
  if not os.path.exists(work_directory):
    os.mkdir(work_directory)
  filepath = os.path.join(work_directory, filename)
  if not os.path.exists(filepath):
    filepath, _ = urllib.request.urlretrieve(SOURCE_URL + filename, filepath)
    statinfo = os.stat(filepath)
    print('Successfully downloaded', filename, statinfo.st_size, 'bytes.')
  return filepath

如果是图片，则处理图片数据

#提取图片到四维uint8数组
def extract_images(filename):
  """Extract the images into a 4D uint8 numpy array [index, y, x, depth]."""
  print('Extracting', filename)
  with gzip.open(filename) as bytestream:
    magic = _read32(bytestream)
    if magic != 2051:
      raise ValueError(
          'Invalid magic number %d in MNIST image file: %s' %
          (magic, filename))
    num_images = _read32(bytestream)
    rows = _read32(bytestream)
    cols = _read32(bytestream)
    buf = bytestream.read(rows * cols * num_images)
    data = numpy.frombuffer(buf, dtype=numpy.uint8)
    data = data.reshape(num_images, rows, cols, 1)
    return data

如果是标签，则处理标签：数字标签数据被解压称1维的tensor: [image index]，它定义了每个样本数值的类别分类

def extract_labels(filename, one_hot=False):
  """Extract the labels into a 1D uint8 numpy array [index]."""
  print('Extracting', filename)
  with gzip.open(filename) as bytestream:
    magic = _read32(bytestream)
    if magic != 2049:
      raise ValueError(
          'Invalid magic number %d in MNIST label file: %s' %
          (magic, filename))
    num_items = _read32(bytestream)
    buf = bytestream.read(num_items)
    labels = numpy.frombuffer(buf, dtype=numpy.uint8)
    if one_hot:
      return dense_to_one_hot(labels)
    return labels

函数——read32需要修改如下;numpy.frombuffer返回为一个数组，这里只需要返回数组值即可。

def _read32(bytestream):
  #采用大尾端存储
  dt = numpy.dtype(numpy.uint32).newbyteorder('>')
  #此处需要修改只返回[0]位置结果  numpy.frombuffer函数返回时一个数组
  return numpy.frombuffer(bytestream.read(4), dtype=dt)[0]

使用tensorflow代码如下：

加载数据集

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

构造线性模型 z=wx+b ，预测输出为y=softmax(z)=softmax(wx+b)

x = tf.placeholder("float", [None, 784])

W = tf.Variable(tf.zeros([784, 10]))

b = tf.Variable(tf.zeros([10]))

y = tf.nn.softmax(tf.matmul(x, W)+b)

代价函数使用交叉熵

  

yi 为预测的分布   yi`为真实分布

y = tf.nn.softmax(tf.matmul(x, W)+b)

y_ = tf.placeholder("float", [None, 10])

cross_entropy = -tf.reduce_sum(y_*tf.log(y))

梯度下降算法来求解最优值

train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

# -*- coding: utf-8 -*-
"""
Created on Sun Nov 18 19:46:33 2018

@author: chen
"""
import input_data
import tensorflow as tf

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

x = tf.placeholder("float", [None, 784])

W = tf.Variable(tf.zeros([784, 10]))

b = tf.Variable(tf.zeros([10]))

y = tf.nn.softmax(tf.matmul(x, W)+b)

y_ = tf.placeholder("float", [None, 10])

cross_entropy = -tf.reduce_sum(y_*tf.log(y))

train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

init = tf.initialize_all_variables()

sess = tf.Session()

sess.run(init)

for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
    
correct_prediction =tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))

accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

print (sess.run(accuracy, feed_dict={x:mnist.test.images, y_:mnist.test.labels}))

随机梯度下降训练：每次选取100样本执行随机梯度下降，迭代1000次

for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})

计算准确率：

correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) 

argmax函数作用：

Returns the index with the largest value across axes of a tensor. (deprecated arguments)

结果correct_prediction为1*10维bool向量，将其转化为为float求其平均值

accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

y为n*10维矩阵，第i行存储着模型对于第i张图片的各种类别预测值

y_存储着第i张图片的类别真实值

最终结果：准确率约为91%

tensorflow的使用规则得学习一下，直接只需定义变量以及代价函数，可用自带算法来执行优化求解真的是牛，以后有机会把算法求解过程源码看一下。

参考地址：

https://www.cnblogs.com/BYRans/p/4905420.html

https://yq.aliyun.com/ziliao/571823

http://www.tensorfly.cn/tfdoc/tutorials/mnist_beginners.html

https://blog.csdn.net/qq_31589695/article/details/79936938