LeetCode每日一题：1222. 可以攻击国王的皇后（2023.9.14 C++）

目录

1222. 可以攻击国王的皇后

题目描述：

实现代码与解析：

模拟

原理思路：

---

1222. 可以攻击国王的皇后

题目描述：

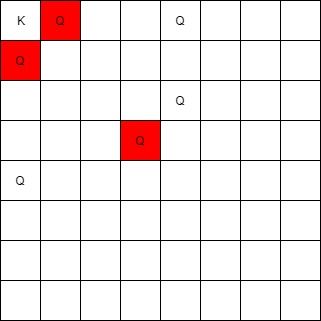
在一个 8x8 的棋盘上，放置着若干「黑皇后」和一个「白国王」。

给定一个由整数坐标组成的数组 queens ，表示黑皇后的位置；以及一对坐标 king ，表示白国王的位置，返回所有可以攻击国王的皇后的坐标(任意顺序)。

示例 1：

输入：queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
输出：[[0,1],[1,0],[3,3]]
解释： 
[0,1] 的皇后可以攻击到国王，因为他们在同一行上。 
[1,0] 的皇后可以攻击到国王，因为他们在同一列上。 
[3,3] 的皇后可以攻击到国王，因为他们在同一条对角线上。 
[0,4] 的皇后无法攻击到国王，因为她被位于 [0,1] 的皇后挡住了。 
[4,0] 的皇后无法攻击到国王，因为她被位于 [1,0] 的皇后挡住了。 
[2,4] 的皇后无法攻击到国王，因为她和国王不在同一行/列/对角线上。

示例 2：

输入：queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
输出：[[2,2],[3,4],[4,4]]

示例 3：

输入：queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
输出：[[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

提示：

• 1 <= queens.length <= 63
• queens[i].length == 2
• 0 <= queens[i][j] < 8
• king.length == 2
• 0 <= king[0], king[1] < 8
• 一个棋盘格上最多只能放置一枚棋子。

实现代码与解析：

模拟

class Solution {
public:
    vector> queensAttacktheKing(vector>& queens, vector& king) {
        
        bool isQueue[8][8] = {false};
        for (auto t: queens) {
            int x = t[0], y = t[1];
            isQueue[x][y] = true;
        }

        vector> res;
        int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1};
        int dy[8] = {1, 0, -1, 1, -1, 1, 0, -1};
        for (int i = 0; i < 8; i++)
        {
            int x = king[0] + dx[i], y = king[1] + dy[i]; // 国王当前位置
            while (x >= 0 && x < 8 && y >= 0 && y < 8)
            {
                if (isQueue[x][y])
                {
                    res.push_back({x, y});
                    break;
                }
                x += dx[i];
                y += dy[i];
            }
        }
        return res;
    }
}

原理思路：

1. 首先，代码定义了一个二维布尔数组 isQueue，用于表示棋盘上的每个位置是否有皇后。数组的大小是8x8，初始值都设置为 false。

2. 接下来，通过一个循环遍历输入参数 queens，其中 queens 是一个表示皇后位置的二维整数向量。循环将每个皇后的位置标记在 isQueue 数组中，将相应位置设为 true。

3. 创建一个空的二维整数向量 res，用于存储可以攻击到国王的皇后的位置。

4. 定义两个一维整数数组 dx 和 dy，它们分别表示了8个可能的方向。dx 用于水平方向的偏移量，dy 用于垂直方向的偏移量。这两个数组用于确定每个方向上国王下一步可能的位置。

5. 通过一个循环遍历8个可能的方向。在每个方向上，从国王的当前位置开始，通过逐步增加 x 和 y 的值来移动。在每一步中，代码检查该位置是否有皇后（通过检查 isQueue[x][y] 的值），如果有皇后，则将该位置添加到 res 中，并且终止该方向的移动（因为皇后可以阻止进一步移动）。

6. 最后，返回存储着可以攻击到国王的皇后位置的 res 二维整数向量。

        核心思想是遍历8个可能的方向，从国王的位置出发，检查每个方向上是否有皇后，如果有就将其位置添加到结果中。这样，最终得到的 res 就包含了可以攻击到国王的皇后的位置坐标。