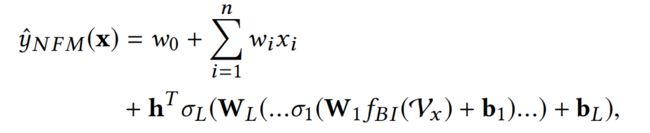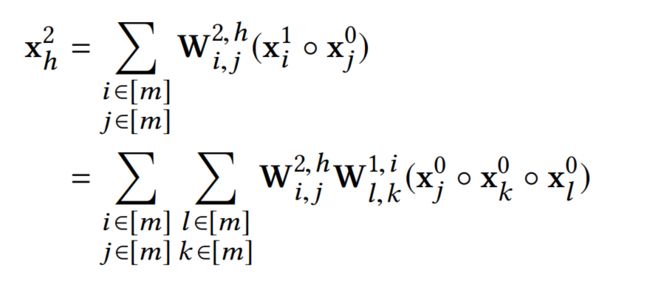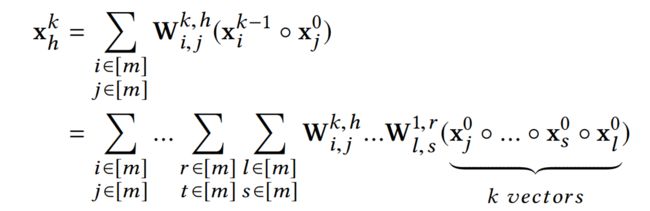CTR预估之Wide&Deep系列(下):NFM/xDeepFM
在上一篇文章中CTR预估之Wide&Deep系列模型:DeepFM/DCN，学习了Wide & Deep这种通用框架：wide组件的线性模型的显性低阶特征交叉提供记忆能力，deep组件的深度网络模型的隐式高阶特征交叉提供泛化能力，还有DeepFM和Deep&Cross（DCN）模型，对wide部分进行改进。
今天，再介绍两种同属这种框架的模型，但改进的不是wide部分，其中NFM（Neural Factorization Machines）是对deep部分的改进，而xDeepFM（eXtreme Deep Factorization Machine）则是引入新的子网络。
NFM
论文：Neural Factorization Machines for Sparse Predictive Analytics
地址：https://arxiv.org/pdf/1708.05027.pdf
- FMs模型的二阶特征交叉是一种线性的方式，论文认为缺乏捕获现实数据中非线性和复杂的内在结构的能力，并且仅实现二阶的特征交叉；
- 而当时2017年，对标的是谷歌提出的Wide&Deep和微软的DeepCrossing，加入了深度神经网络，虽然拥有了学习非线性的高阶特征交叉的能力，但是作为神经网络的输入：特征embeddings的简单拼接，在底层携带的特征交叉信息过少，并且存在梯度消失/爆炸、过拟合等问题，使训练变得困难。
- 因此，提出了NFM（Neural Factorization Machines）模型，既拥有FM二阶特征交叉的线性建模能力(底层)，又拥有神经网络的高阶特征交叉的非线性建模能力。
NFM的wide部分，其实与谷歌的Wide&Deep模型是一样的，只是简单的线性模型，如下式：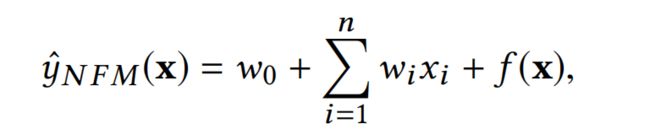
其创新点主要在deep部分f(x)，其deep部分如下图所示，加入了Bi-Interaction Pooling，而不是像常规神经网络，输入仅仅是特征embeddings的拼接。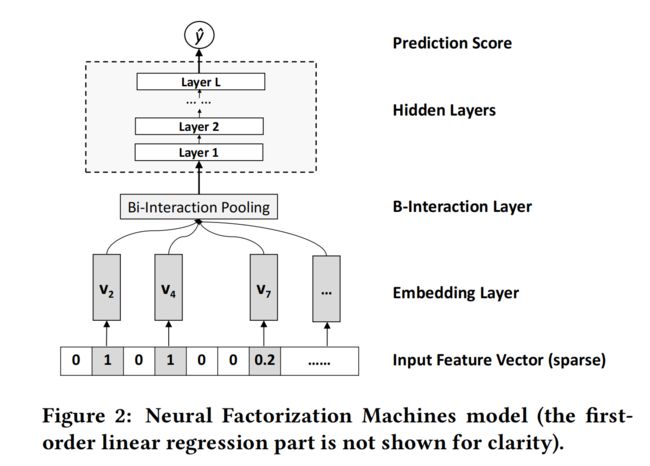
下面，我们就着重介绍Bi-Interaction Pooling部分，其它部分与Wide&Deep系列都是一样的，不再赘述。
Bi-Interaction Pooling
Bi-Interaction Pooling其实是FM模型的二阶特征交叉部分，可以认为是将所有embeddings vectors集合 V x V_x Vxpooling为一个vector，是一个k维的向量，编码了特征emebddings二阶交互，具体公式如下：
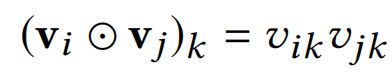
接着，经过Bi-Interaction Pooling之后的k维向量作为神经网络的输入：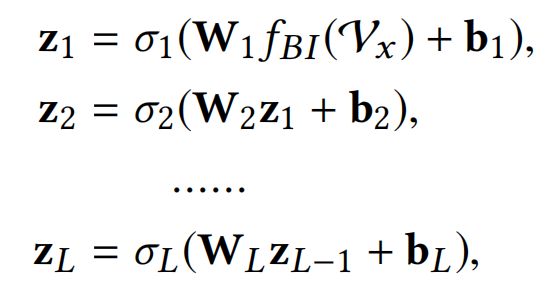
最后，加入线性部分，NFM模型的完整表达式为：
到这里，我们可以看出，NFM去掉神经网络层，那么等同于FM模型；如果将Bi-Interaction Pooling替换为拼接操作，再接MLP或者残差网络，那么NFM则可以还原Wide&Deep或者DeepCrossing。
xDeepFM
论文：xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems
地址：https://arxiv.org/pdf/1803.05170.pdf
为了学习高阶的特征交互，往往是引入DNN模块，如Wide&Deep、DeepFM等等，但是论文认为DNN对高阶特征交互的建模是一种隐式的方式，最后学到的function可能是随心所欲的(arbitrary)，并且没有理论的结论说明特征交互能达到的最高阶，另外这是bit-wise级别的，以FM框架的vector-wise不同。
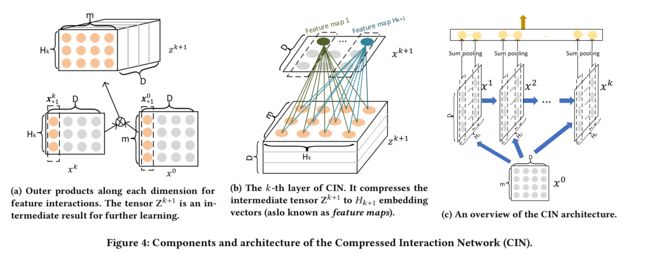
因此，xDeepFM（eXtreme Deep Factorization Machine）提出了一种能够在vector-wise级别上，显式地捕获特征交互，并且可以达到界定阶数的子网络：Compressed Interaction Network (CIN)，并且还带有CNN和RNN的部分能力。其结构如下图：
Cross Network的缺点
Deep & Cross(DCN)提出了一种显示学习高阶特征交互的方法Cross Network，具体如下式：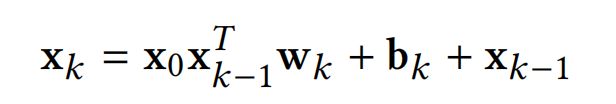
但是，Cross Network存在以下两个缺点：
- 对于一个k层的Cross Network，每一层网络的输出 x k x_k xk其实都是 x 0 x_0 x0的标量乘积(见下证明)，但这不意味着 x k x_k xk是 x 0 x_0 x0的线性关系， x k x_k xk的系数 α i + 1 \alpha^{i+1} αi+1与 x 0 x_0 x0相关敏感的，但 x 0 x_0 x0并不是模型的参数；
- 特征交叉是一种bit-wise的方式，那么同一个field embedding的每个bit都会相互影响。
Compressed Interaction Network
针对DCN中的Cross Network存在的缺点，论文设计了一种新的交叉网络Compressed Interaction Network (CIN)，具有以下优点：
- 特征交互是应用在vector-wise级别的，而不是bit-wise；
- 高阶的特征交互是显式的；
- 网络复杂度不会随着特征交互的阶数增加而增加。
The output of the k-th layer in CIN. CIN的输入是由field embedding组成的矩阵 X 0 ∈ R m × D ， X 0 X_0\in \mathbb{R}^{m\times D}，X_0 X0∈Rm×D，X0的第i行则是第i个field的embedding vector： X i , ∗ 0 = e i X^0_{i,*}=e_i Xi,∗0=ei ，D则是field embedding的维度。
第k层CIN的输出仍然是一个矩阵 X k ∈ R H k × D ， H k X_k\in \mathbb{R}^{H_k\times D}，H_k Xk∈RHk×D，Hk代表第k层的embedding vectors的数量， H 0 = m H_0=m H0=m。那么，对于每层网络的输出 X k X_k Xk计算公式为下式：
其中， 1 ≤ h ≤ H k ， W k , h ∈ R H k − 1 × m 1\le h \le H_k，W^{k,h}\in \mathbb{R}^{H_{k-1}\times m} 1≤h≤Hk，Wk,h∈RHk−1×m是第h个特征向量(第k层CIN网络)的参数矩阵。 ∘ \circ ∘为哈达玛积（Hadamard product)： < a 1 , a 2 , a 3 > ∘ < b 1 , b 2 , b 3 > = < a 1 b 1 , a 2 b 2 , a 3 b 3 >
从 X k X_k Xk计算公式可以看出：
- X k X_k Xk是通过 X k − 1 和 X 0 X_{k-1}和X_0 Xk−1和X0哈达玛积交叉而来，这种特征交互明显是显式，并且阶数随着CIN的层数增加而增加
- 由于特征交叉是哈达玛积的形式，这决定它是vector-wise，因为同一个embedding vector的bit不会相互交叉，只会与其它embedding vector的bit进行交叉
Sum Pooling. 如下图[CIN图解-c]，计算k层CIN隐藏层输出之后，还会在CIN隐藏层的embedding vector维度上进行sum pooling，得到 p + p^+ p+作为CIN的最终输出：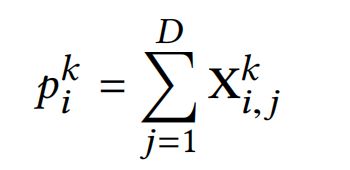
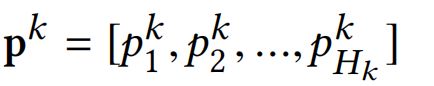
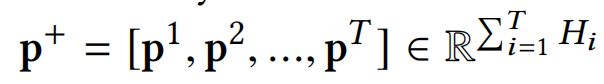
前面还提到CIN还具有RNN和CNN的部分特性，下面我们进行分析：
- Recurrent Neural Network (RNN)的特点之一是下一个隐藏层的输出依赖于上一个隐藏层和一个补充的输入，这是与CIN结构很相似的；
- CIN与Convolutional Neural Networks (CNNs)也是有着许多紧密的关联。引入一个中间张量 Z k + 1 Z^{k+1} Zk+1，作为 X k 和 X 0 X_k和X_0 Xk和X0的outer product。它可以看作一种特殊类型的图像- H k H_k Hk个通道的 m × D m\times D m×D像素点矩阵，正如上图[CIN图解-a]。然后 W k , h W^{k,h} Wk,h则对应是一个滤波器(filter)，沿着embedding维度(D)移动(slide)滤波器，如上图[CIN图解-b]，然后得到 X h , ∗ k X^k_{h,*} Xh,∗k，这在计算机视觉领域被称为feature map，因此 X k X_k Xk则是 H k H_k Hk个不同的feature map的集合。
Combination
虽然论文提出了DNN是否为对高阶特征交互建模的最有效模型的提问，但还是保留DNN模块，提供隐式的高阶特征交互能力，提升泛化能力。最终，xDeepFM会组合线性模型+CIN+DNN，它的输出为下式：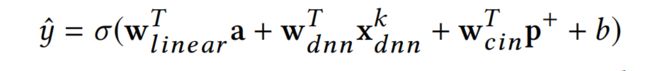
再回顾上图[xDeepFM结构]，可以看出，xDeepFM其实是在Wide&Deep引入了新的子网络-CIN；而当CIN的深度和feature maps数量都为1时，xDeepFM就会退化为DeepFM，唯一不同的只是xDeepFM会为线性部分、交叉网络和DNN学习不同的权重，而DeepFM对于这三部分则是直接链接到输出，没有系数。
多项式分析
接下来，仍然与DCN的Cross Network一样，通过多项式的角度来对CIN的特征交叉阶数进行分析。简化一下，每一层的feature maps数量都为m，那么第一层的第h个feature map计算公式如下式：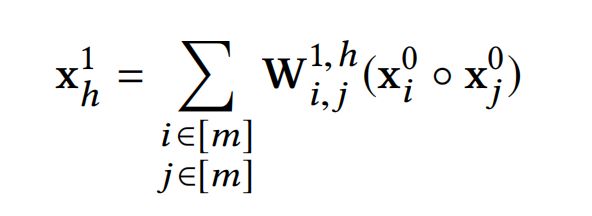
其中， x h 1 ∈ R D ， [ m ] x^1_h\in \mathbb{R}^D，[m] xh1∈RD，[m]为小于等于m的正数集合。可以看出，每个对特征对交叉(pair-wise)建模的feature map都有着 O ( m 2 ) O(m^2) O(m2)个系数。
同样的，第二层的第h个feature map如下式：
一个k阶的多项式会有 O ( m k ) O(m^k) O(mk)个系数，而CIN能够用a chain of feature maps，以 O ( k m 2 ) O(km^2) O(km2)的参数量达到k阶多项式的效果。(论文写的参数量是 O ( k m 3 ) O(km^3) O(km3)，不知道是否写错，我个人理解是 O ( k m 2 ) O(km^2) O(km2)，望有大佬指出)。下面，则需要进一步分析下k层的CIN是否也拥有 O ( m k ) O(m^k) O(mk)个系数。
第k层的第h个feature map计算如下式：
为了更好的对比阐述，论文还是引用Deep & Cross(DCN)中的符号， α = [ α 1 , . . . , α m ] ∈ N d \alpha=[\alpha_1,...,\alpha_m]\in \mathbb{N}^d α=[α1,...,αm]∈Nd代表特征交叉项的索引， ∣ α ∣ = ∑ i m α i |\alpha|=\sum_i^m\alpha_i ∣α∣=∑imαi为交叉阶数。
使用 x i x_i xi来表示 x i 0 x_i^0 xi0，因为feature maps表达式展开之后都是来自第0层网络(field embeddings)。上标表示向量交叉操作，如 x i 3 = x i ∘ x i ∘ x i x^3_i=x_i \circ x_i \circ x_i xi3=xi∘xi∘xi，那么，k阶的向量多项式如下式：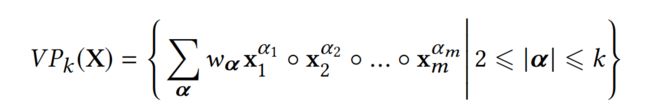
每个向量多项式都有 O ( m k ) O(m^k) O(mk)个系数，CIN的系数 w α w_{\alpha} wα如下式：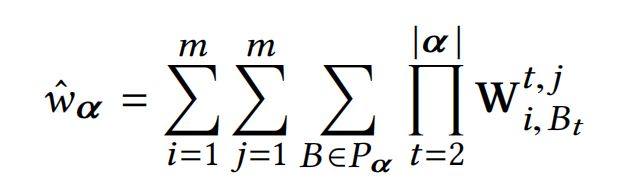
其中， B = [ B 1 , B 2 , . . . , B ∣ α ∣ ] ， P α = ( 1 , . . . , 1 ⏟ α 1 t i m e s . . . m , . . . , m ⏟ α m t i m e s ) B=[B_1,B_2,...,B_{|\alpha|}]，P_{\alpha}=(\underbrace{1,...,1}_{\alpha_1\ times}...\underbrace{m,...,m}_{\alpha_m\ times}) B=[B1,B2,...,B∣α∣]，Pα=(α1 times 1,...,1...αm times m,...,m)，是交叉项索引的所有排列组合
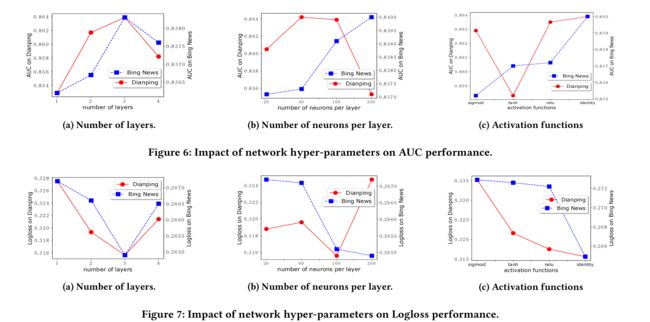
实验结果
总结
在Wide&Deep的框架基础上：
- DeepFM和Deep&Cross（DCN）模型是在对wide部分进行改进，分别使用FM和显式高阶特征交叉的Cross Network；
- 这篇文章的NFM（Neural Factorization Machines）是对deep部分的改进，使用FM的field embeddings二阶特征交叉来代替简单拼接，为底层提供更多的特征交叉信息；
- xDeepFM（eXtreme Deep Factorization Machine）则是引入新的子网络CIN，改进了DCN交叉网络的缺点，具有高效的显式高阶特征交叉能力，并且是vector-wise级别的。
代码实现
GitHub