非线性世界的探索：多项式回归解密

什么是多项式回归？

多项式回归是一种回归分析方法，用于建立因变量（目标）和自变量（特征）之间的关系。与线性回归不同，多项式回归假设这种关系不是线性的，而是一个多项式函数。多项式回归的一般形式如下：

其中：

• y 是因变量（目标）。
• x 是自变量（特征）。
• β0,β1,…,βn​ 是多项式的系数。
• ϵ 是误差项，表示模型无法完美拟合数据的部分。

多项式回归的关键之处在于它允许我们通过增加多项式的阶数（nn）来适应不同程度的非线性关系。

多项式回归的应用

多项式回归在许多领域都有广泛的应用，包括但不限于以下几个方面：

• 自然科学：多项式回归可用于建模物理、化学和生物学等领域的非线性关系，例如动力学方程。

• 金融：在金融领域，多项式回归可以用来预测股票价格、汇率和投资组合的表现，因为这些数据通常受多种复杂因素的影响。

• 医学：多项式回归可以用于分析医学数据，例如药物吸收速率与剂量之间的关系。

• 工程：在工程领域，多项式回归可用于建立复杂系统的模型，以改进设计和性能。

实现多项式回归

首先我们可以先创建一个曲线，先看看
这里我们先导入需要的库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

之后我们创建一个曲线并绘制

x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.5*x**2+x+3+np.random.normal(0,1,size=100)
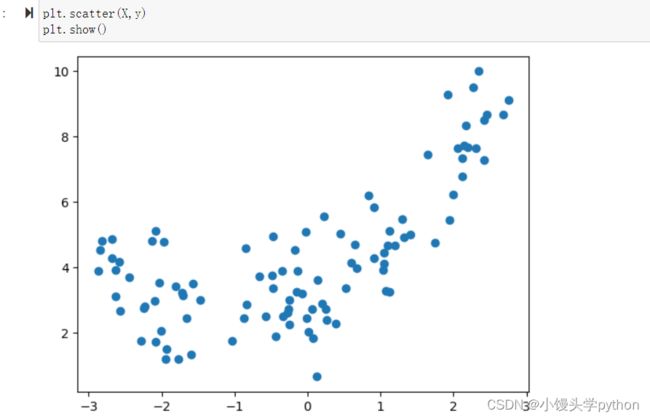
plt.scatter(X,y)
plt.show()

运行结果如下

接下来我们使用线性回归进行拟合

X_train,X_test,y_train,y_test = train_test_split(X,y)
lin_reg = LinearRegression()
lin_reg.fit(X_train,y_train)
y_predict = lin_reg.predict(X)

接下来我们看看具体得分是多少

结果显而易见差的一批

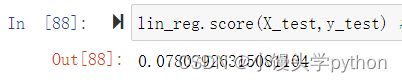
再来看看它的均方误差

结果也是比较大的，最后我们来看一眼绘制好的直线

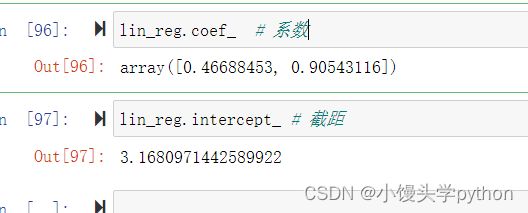
接下来我们在原来数据集的基础上，增加y一列特征,得到新的样本集X2，依然套用线性回归的模型

X2 = np.hstack([X**2,X])

再得出均方误差就小了许多

再来看看绘制后的图像

再来看看系数和截距，还是比较准确的

sklearn中封装的多项式特征

首先还是导入库

from sklearn.preprocessing import PolynomialFeatures

之后我们要去创建一个多项式特征生成器对象ploy

poly = PolynomialFeatures(degree=2)
poly.fit(X)
X_poly = poly.transform(X)

• poly = PolynomialFeatures(degree=2)：
  这一行创建了一个多项式特征生成器对象 poly。
  degree=2 参数指定了要生成的多项式的最高次数。在这里，它被设置为2，表示我们将生成所有原始特征的平方项以及它们的交叉项。

• poly.fit(X)：
  这一行将多项式特征生成器 poly 与输入数据集 X 进行拟合（适应）。
  在这个步骤中，多项式特征生成器会学习如何将输入数据集中的特征转换为多项式特征。

• X_poly = poly.transform(X)：
  这一行使用已经拟合好的多项式特征生成器 poly 来将原始特征数据集 X 转换为多项式特征数据集 X_poly。
  这里的 X_poly 包含了原始特征的各阶多项式，例如，如果原始特征是 x1 和 x2，那么 X_poly 包含 x1^2、x22 以及 x1*x2 等项，根据指定的 degree 参数而生成。

当然我们也可以看看具体的数据，这样方便观察

X_poly[:3,:]

运行结果如下

注意：进行多项式计算以后，得到的数据集需要做数据的归一化

进行多项式计算后，得到的数据集通常需要进行数据归一化或标准化，主要有以下几个原因：

• 防止数值范围差异过大：多项式特征生成可能会导致特征之间的数值范围差异变得非常大。例如，平方项和交叉项可能会产生远大于原始特征的值。如果不进行归一化，模型可能会因为特征之间的数值范围差异而受到影响，导致模型训练困难，甚至无法收敛。

• 提高模型性能：许多机器学习算法对于特征的数值范围敏感，可能会更关注数值范围较大的特征，而忽略数值范围较小的特征。这可能会导致模型在预测时表现不佳。通过归一化，可以确保所有特征在相似的数值范围内，使模型更容易学习特征之间的关系。

• 加速模型收敛：在许多优化算法中，归一化可以帮助模型更快地收敛到最优解。当特征具有相似的数值范围时，梯度下降等优化算法通常更加稳定和高效。

在sklearn中使用管道

导入库

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

创建管道对象，根据先后顺序对数据进行多项式处理，归一化处理和线性回归训练处理

poly_reg = Pipeline([    
    ('poly',PolynomialFeatures(degree=2)),
    ('std_scaler',StandardScaler()),
    ('lin_reg',LinearRegression())
])

最后进行实现

x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.5*x**2+x+3+np.random.normal(0,1,size=100)
X_train,X_test,y_train,y_test = train_test_split(X,y)
poly_reg.fit(X_train,y_train)
y_predict = poly_reg.predict(X)
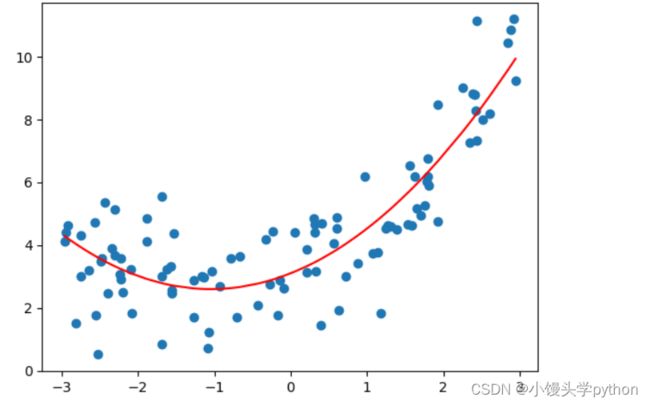
plt.scatter(X,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
plt.show()

运行结果如下

挑战与创造都是很痛苦的，但是很充实。