浅谈线段树

列表

前置知识

线段树是什么？

线段树的思想

最初的最初（$\text{pushup}$）

建树（$\text{build}$）

查询（$\text{query}$）

更新（$\text{update}$）

优化 $1$（$\text{lazy-tag}$）

优化 $2$（标记永久化）

最后的最后（空间提醒 & 时间复杂度说明）

代码

扩展

可持久化线段树/主席树

可持久化线段树有什么用

可持久化线段树的思想

建树（$\text{build}$）

更新（$\text{update}$）

查询（$\text{query}$）

最后（空间复杂度分析）

代码

疑问 & 催更

前置知识

1. 了解位运算（为线段树优化做铺垫）。
2. 了解堆。
3. 了解树。

如果您还没有学完，就可以不用看下面的内容了。

线段树是什么？

• 线段树是一种可以解决区间问题的利器。

• 线段树是一种高级数据结构。

• 线段树是一种二叉搜索树（来源于网上）。

只不过以上这些都是介绍，其实真正的线段树并没有那么恐怖。

线段树的思想

线段树（segment tree），又名区间树。我们可以通过一个题目来直观的了解它：P3372。

我们按照常规思路想：

1. 暴力，时间复杂度 $O(N^2)$。

2. 前缀和，由于有修改操作，所以时间复杂度为 $O(N^2)$。

这个复杂度是我们不可接受的，所以我们用线段树来解决这个问题。

我们假设原来的序列为：

8
1 9 3 1 2 5 2 2

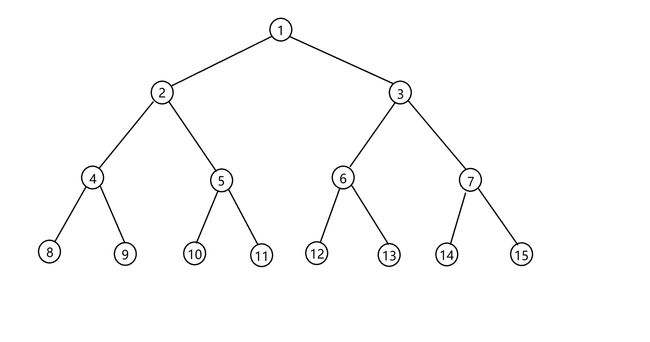
线段树，顾名思义，首先要建一棵二叉树：

一定要注意是二叉树。

这棵树按照堆式存储来编号，一共有 $15$ 个节点。

然后我们赋予它每个节点一点值，并且把值记录为 $tree$：

每个节点旁边的一个区间代表这个节点的值是这个区间的和，例如 $tre{e}_5=4$。

那么区间又有什么特殊的性质呢？假设一个节点所代表的区间是 $[l,r]$，那么它的两个子节点的区间就分别是 $[l,(l+r>>1)]$，$[(l+r>>1),r]$。就是分治的思想。

线段树的意义就讲完了，接下来将如何实现。

最初的最初（$\text{pushup}$）

$\text{pushup}$ 是一个函数，表示向上更新的意思，每次可以更新节点 $cur$ 的值。

$\text{pushup}$ 代码：

void pushup(int cur)
{
    tree[cur] = tree[cur << 1] + tree[(cur << 1) + 1];   //更新
    return ;
}

其实就是一个回溯操作。

建树（$\text{build}$）

这里非常简单，就是不断的分治/递归下去，最后再用 $\text{pushup}$ 更新就可以了。

注意，到了叶子节点可以直接返回值。

$\text{build}$ 代码：

void build(int cur, int lt, int rt) //cur 为树上节点，管辖 [lt, rt] 的数列区间
{
    if(lt == rt)   //递归到叶子节点
    {
        tree[cur] = a[lt];
        return ;
    }
    int mid = lt + rt >> 1;
    build(cur << 1, lt, mid);   //继续分治/递归
    build((cur << 1) + 1, mid + 1, rt);
    pushup(cur);  //向上传递结果
    return ;
}

这里时间复杂度为 $O(4N)$。

查询（$\text{query}$）

举个例子。

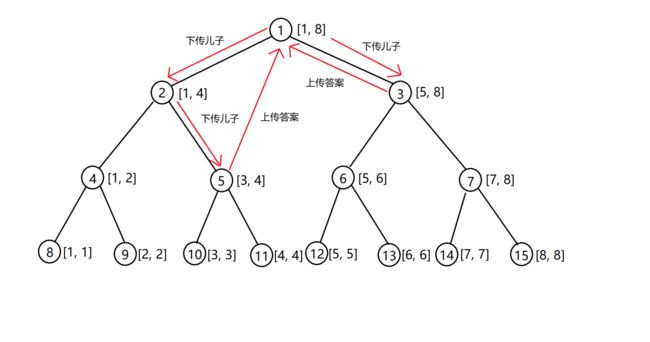
就比如说查询区间 $[3,8]$，我们首先把问题看到节点 $1$。节点 $1$ 说我管得范围太大了，得让我的两个儿子来解决。然后节点 $2$ 说，我也解决不了，又得给我的两个儿子解决。节点 $4$ 说这事跟我没关系，但节点 $5$ 说我正好就是问题中的一部分，可以解决。再来看节点 $3$，它说我也可以正好解决。所以询问的结果就是 $tre{e}_5+tre{e}_3$。

从上述讲话中来看，其实就是不断的传儿子，只要在区间内就返回。

画图表示一下：

所以查询操作到的每个区间就只有三种选择：

1. 询问的区间 $[x,y]$ 和这个节点所覆盖的区间 $[lt,rt]$ 根本没有关系。

图示如下：

2. 询问的区间 $[x,y]$ 和这个节点所覆盖的区间 $[lt,rt]$ 是完全包含的关系。

图示如下：

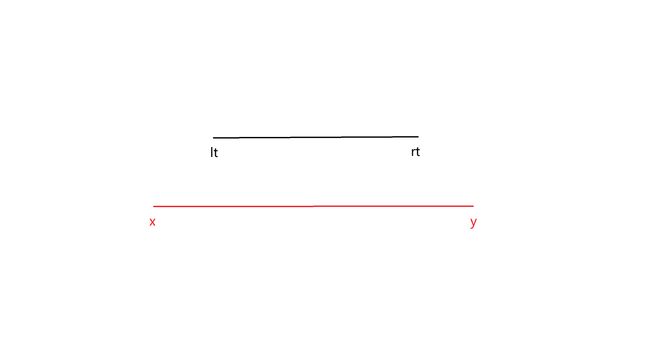
3. 问的区间 $[x,y]$ 和这个节点所覆盖的区间 $[lt,rt]$ 是部分包含的关系。

图示如下：

此时我们只有当区间是 $3$ 的情形时才下传。

所以我们的代码就可以这么写：

int query(int cur, int lt, int rt, int x, int y) //cur 代表当前的节点，lt, rt 表示这个节点所管辖的区间，x, y 表示我要询问的区间
{
    if(x > rt || y < lt) //都已经没有关系了，直接返回 0
    {
        return 0;
    }
    if(x <= lt && rt <= y) //是 [x, y] 的一部分
    {
        return tree[cur];
    }
    int mid = lt + rt >> 1;   //向左右儿子请求答案
    return query(cur << 1, lt, mid, x, y) + query((cur << 1) + 1, mid + 1, rt, x, y);
}

这里时间复杂度是 $O({\log }_{2}N)$ 的。

更新（$\text{update}$）

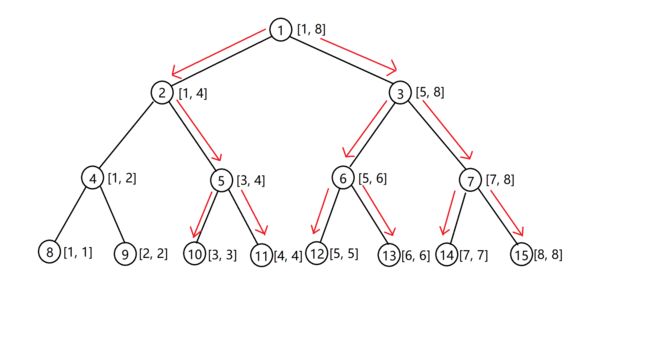
再来举个例子，更新 $[3,8]$。

我们不断地下传给儿子，直到到了叶子节点之后，然后再向上更新。

这个思路应该很好理解，就是把所有点所在的叶子节点都改完后，再上传更新。

画图表示一下：

然后我们更新又分为三点：

1. 更新区间 $[x,y]$ 与这个节点管辖的区间 $[lt,rt]$ 没有关系。

这里的图示与查询一样。

2. 更新区间 $[x,y]$ 与这个节点管辖的区间 $[lt,rt]$ 是完全包含且 $lt=rt$。

这里作者不画，请自行脑补（bushi）。

其实就是到达了叶子节点。

3. 更新区间 $[x,y]$ 与这个节点管辖的区间 $[lt,rt]$ 是部分包含关系。或者是完全包含但是 $lt\ne rt$。

这里的图示也与查询一样。

然后只有当情况 $3$ 发生才传递给左右孩子。

$\text{update}$ 代码：

void update(int cur, int lt, int rt, int x, int y, int val) //在 [x, y] 的区间元素均加 val
{
    if(x > rt || y < rt) // 没有任何关系
    {
        return ;
    }
    if(lt == rt && x <= lt && rt <= y) //是叶子节点，且落在 [x, y] 内
    {
        tree[cur] += val;
        return ;
    }
    int mid = lt + rt >> 1;
    update(cur << 1, lt, mid, x, y, val);
    update((cur << 1) + 1, mid + 1, rt, x, y, val);
    pushup(cur); //cur 的左右孩子有可能修改了，那么 cur 管辖的区间和要更新
    return ;
}

这里的时间复杂度为 $O(4N)$。

优化 $1$（$\text{lazy-tag}$）

我们发现，虽然建树和查询的时间复杂度是很低的，但是更新的时间复杂度很高，连暴力都比不上。

我们思考更新的时间高的原因，是因为你把每个元素都给更新了，而如果后面又没有查询这段区间，那岂不是就亏了。

所以，总结一段话：修改是为询问而服务的。

所以就诞生了 $\text{lazy-tag}$ 这个东西（没错，就是懒~标记）。

我们可以记录一个数组 $tag$，来记录每个节点的懒标记数值。所以，只要还没有查询到，这个懒标记就一直在睡觉~~（bushi）。

又来举上面那个例子，更新区间 $[3,8]$，此时，我们发现节点 $5$ 和节点 $3$ 是被完全包含的，所以我们就把更新的值放在节点 $5$ 和节点 $3$ 上面，先把自己的值给加了（注意，一定要先把自己的值先加上），然后再把 $\text{lazy-tag}$ 加上要更新的值，等到以后有机会再还给儿子节点。

那么给出打懒标记的函数：

void addtag(int cur, int lt, int rt, int val) //cur，[lt, rt] 元素加 val
{
    tag[cur] += val;  //加上以后要还给儿子们每个多少值
    tree[cur] += (rt - lt + 1) * val;   //这里要给自己加上
    return ;
}

然后有人就问了，你这个懒标记总不能放在这里不动呀！那查询或更新的时候怎么办？没错，懒标记在这个时候的勤快了，在查询或更新的途中就顺便还“债”，把差的值还给儿子节点，同时又在儿子节点上打上标记，然后循环往复。

所以懒标记核心就一句话：只要你不查询，我就在这里睡觉，只要你一查询，我就托你顺便带给儿子节点。

然后给出下放标记（俗称托人带物，有个专业名词叫 $\text{pushdown}$）函数代码：

void pushdown(int cur, int lt, int rt) //lt, rt 表示 cur 节点所管辖的区间
{
    if(tag[cur] == 0) //这里很重要，当没有标记，也就是为 0 时，就不要向下传了（有的题目不加会错）
    {
        return ;
    }
    int mid = lt + rt >> 1;
    addtag(cur << 1, lt, mid, tag[cur]); //给左右孩子打标记
    addtag((cur << 1) + 1, mid + 1, rt, tag[cur]);
    tag[cur] = 0;   //最后还掉一身的债
    return ;
}

然后我们的 $\text{query}$ 和 $\text{update}$ 都要改一下：

$\text{query}$：

int query(int cur, int lt, int rt, int x, int y) //cur 代表当前的节点，lt, rt 表示这个节点所管辖的区间，x, y 表示我要询问的区间
{
    if(x > rt || y < lt) //都已经没有关系了，直接返回 0
    {
        return 0;
    }
    if(x <= lt && rt <= y) //是 [x, y] 的一部分
    {
        return tree[cur];
    }
    pushdown(cur, lt, rt); //在这里下放标记，位置一定不能错
    int mid = lt + rt >> 1;   //向左右儿子请求答案
    return query(cur << 1, lt, mid, x, y) + query((cur << 1) + 1, mid + 1, rt, x, y);
}

$\text{update}$：

void update(int cur, int lt, int rt, int x, int y, int val) //在 [x, y] 的区间元素均加 val
{
    if(x > rt || y < rt) // 没有任何关系
    {
        return ;
    }
    if(x <= lt && rt <= y) //是被完全包含，打懒标记
    {
        addtag(cur, lt, rt, val);
        return ;
    }
    pushdown(cur, lt, rt);   //只要向下递归就要 pushdown
    int mid = lt + rt >> 1;
    update(cur << 1, lt, mid, x, y, val);
    update((cur << 1) + 1, mid + 1, rt, x, y, val);
    pushup(cur); //cur 的左右孩子有可能修改了，那么 cur 管辖的区间和要更新
    return ;
}

首先为什么 $\text{query}$ 和 $\text{update}$ 的 $\text{pushdown}$ 要放在那个位置，因为无论你时询问还是更新，只要向下递归就会下传。

至于 $\text{update}$ 的，当然是要在完全包含时才能 $\text{addtag}$ 的啦！

使用 $\text{lazy-tag}$ 之后时间复杂度会降到 $O({\log }_{2}N)$（原理和查询一样）。

优化 $2$（标记永久化）

线段树最出名的就是 $\text{lazy-tag}$ 了，它的优秀时间复杂度和实用性可以应对大多数情况。

而标记永久化呢？就是应对那些小部分情况。比如主席树区间修改，树套树（这里指线段树相套）矩阵修改。

标记永久化和 $\text{lazy-tag}$ 的区别：

1. 拒绝下传标记。

2. 不一定每个区间的 $tree$ 加上 $tag$ 都是相对正确的。

那么我们如何不用标记下传呢？

1. 我们的标记的值要加上 $tag\times (rt-lt+1)$，并且要上传标记所带来的值。

所以我们的 $\text{pushup}$ 就要改造一番：

void pushup(int node, int lt, int rt){
  tree[node] = tree[node << 1] + tree[node << 1 | 1] + (rt - lt + 1) * tag[node];
}

这里就是在左右儿子的基础上加上这个节点的标记所给它带来的影响。

那么我们的 $\text{update}$ 也要改造一番：

void update(int node, int lt, int rt, int x, int y, int val){
  if(y < lt || x > rt){
    return ;
  }
  if(x <= lt && rt <= y){
    tag[node] += val;   //标记 += val，并且拒绝下传，直接 return ;
    tree[node] += (rt - lt + 1) * val;   //这个节点要加上值
    return ;
  }
  int mid = lt + rt >> 1;
  update(node << 1, lt, mid, x, y, val);
  update(node << 1 | 1, mid + 1, rt, x, y, val);
  pushup(node, lt, rt);
}

2. 对于查询，我们只需要在一路时来加上相应的区间长度乘上这个区间的 $tag$ 就可以了，利用一顿数学乱搞，就可以证明这样是对的（建议自己手推）。最后就是注意由于完全包含的已经加了，所以就不用再加一遍了。

这里可以自己动手画画图，就可以明白了：

int query(int node, int lt, int rt, int x, int y){
  if(y < lt || x > rt){
    return 0;
  }
  if(x <= lt && rt <= y){
    return tree[node];
  }
  int mid = lt + rt >> 1;
  return (min(rt, y) - max(lt, x) + 1) * tag[node] + query(node << 1, lt, mid, x, y) + query(node << 1 | 1, mid + 1, rt, x, y);
}

标记永久化其实在现实中用得不多，出题人也不会去出这些稀奇古怪得题目（除非是出题人脑袋有病，诚心卡你），所以这一章节也没有什么用啦！

最后的最后（空间提醒 & 时间复杂度说明）

这里先说一下，$tree$ 和 $tag$ 都要开 $4N$ 这么大。

证明：

一棵完全二叉树的节点数量为 $2N-1$（这个可以自己 baidu），又因为线段树可能不是完全二叉树，可能多出 $2N-1$ 个叶子节点，所以一共就是 $4N-2$，差不多就是 $4N$。

所以最初的建树与更新都是 $O(4N)$ 的复杂度。

代码

这里给出 线段树 $1$ 的所有代码（相信没有人会看吧）。

代码 $1$（$\text{lazy-tag}$）：

#include
#define int long long    //只提醒这里，要开 long long

using namespace std;

const int N = 1e5 + 5;

int n, m;
int a[N];

int tree[N * 4], tag[N * 4];

void pushup(int node){
  tree[node] = tree[node << 1] + tree[node << 1 | 1];
}

void addtag(int node, int lt, int rt, int val){
  tag[node] += val;
  tree[node] += (rt - lt + 1) * val;
}

void pushdown(int node, int lt, int rt){
  if(!tag[node]){
    return ;
  }
  int mid = lt + rt >> 1;
  addtag(node << 1, lt, mid, tag[node]);
  addtag(node << 1 | 1, mid + 1, rt, tag[node]);
  tag[node] = 0;
}

void build(int node, int lt, int rt){
  if(lt == rt){
    tree[node] = a[lt];
    return ;
  }
  int mid = lt + rt >> 1;
  build(node << 1, lt, mid);
  build(node << 1 | 1, mid + 1, rt);
  pushup(node);
}

void update(int node, int lt, int rt, int x, int y, int val){
  if(x > rt || y < lt){
    return ;
  }
  if(x <= lt && rt <= y){
    addtag(node, lt, rt, val);
    return ;
  }
  pushdown(node, lt, rt);
  int mid = lt + rt >> 1;
  update(node << 1, lt, mid, x, y, val);
  update(node << 1 | 1, mid + 1, rt, x, y, val);
  pushup(node);
}

int query(int node, int lt, int rt, int x, int y){
  if(x > rt || y < lt){
    return 0;
  }
  if(x <= lt && rt <= y){
    return tree[node];
  }
  pushdown(node, lt, rt);
  int mid = lt + rt >> 1;
  return query(node << 1, lt, mid, x, y) + query(node << 1 | 1, mid + 1, rt, x, y);
}

void Solve(){
  cin >> n >> m;
  for(int i = 1; i <= n; i++){
    cin >> a[i];
  }
  build(1, 1, n);
  while(m--){
    int op;
    cin >> op;
    if(op == 1){
      int x, y, k;
      cin >> x >> y >> k;
      update(1, 1, n, x, y, k);
    }
    else{
      int x, y;
      cin >> x >> y;
      cout << query(1, 1, n, x, y) << '\n';
    }
  }
}

signed main(){
  Solve();
  return 0;
}

代码 $2$（标记永久化）：

#include
#define int long long

using namespace std;

const int N = 1e5 + 5;

int n, m;
int a[N];

int tree[N * 4], tag[N * 4];

void pushup(int node, int lt, int rt){
  tree[node] = tree[node << 1] + tree[node << 1 | 1] + (rt - lt + 1) * tag[node];
}

void build(int node, int lt, int rt){
  if(lt == rt){
    tree[node] = a[lt];
    return ;
  }
  int mid = lt + rt >> 1;
  build(node << 1, lt, mid);
  build(node << 1 | 1, mid + 1, rt);
  pushup(node, lt, rt);
}

void update(int node, int lt, int rt, int x, int y, int val){
  if(y < lt || x > rt){
    return ;
  }
  if(x <= lt && rt <= y){
    tag[node] += val;
    tree[node] += (rt - lt + 1) * val;
    return ;
  }
  int mid = lt + rt >> 1;
  update(node << 1, lt, mid, x, y, val);
  update(node << 1 | 1, mid + 1, rt, x, y, val);
  pushup(node, lt, rt);
}

int query(int node, int lt, int rt, int x, int y){
  if(y < lt || x > rt){
    return 0;
  }
  if(x <= lt && rt <= y){
    return tree[node];
  }
  int mid = lt + rt >> 1;
  return (min(rt, y) - max(lt, x) + 1) * tag[node] + query(node << 1, lt, mid, x, y) + query(node << 1 | 1, mid + 1, rt, x, y);
}

void Solve(){
  cin >> n >> m;
  for(int i = 1; i <= n; i++){
    cin >> a[i];
  }
  build(1, 1, n);
  while(m--){
    int op;
    cin >> op;
    if(op == 1){
      int x, y, k;
      cin >> x >> y >> k;
      update(1, 1, n, x, y, k);
    }
    else{
      int x, y;
      cin >> x >> y;
      cout << query(1, 1, n, x, y) << '\n';
    }
  }
}

signed main(){
  Solve();
  return 0;
}

应该讲得很清楚（过于自信）。

扩展

使用线段树还可以解决区间最大值，最小值，最大公约数等问题。使用线段树解决的问题必须满足区间加法（这是重点）。

所谓区间加法。设 $[l,r]$，并且 $mid$ 是中点（$l+r>>1$），打个比方：

$[l,mid]$ 的和 $+$ $[mid+1,r]$ 的和等于 $[l,r]$ 的和。

区间加法就是这个意思。

可持久化线段树/主席树

听说主席树这个名字是 OIer 们在谈论政治的时候发明了这个玩意。

可持久化线段树有什么用

可持久化线段树可以保存每一个历史版本的线段树，使得可以在每一个历史版本上做查询和修改。

简单来说，就是可以后悔。

可持久化线段树的思想

我们还是通过一个例题来了解它：P3919。

我们可以发现什么？

我们可以发现这些东西：

1. 每次只有单点赋值。

2. 每次只有单点查询。

3. 涉及到每个历史版本的保存。

那么，如何保存每个历史版本呢？

如果针对每一次操作开一棵线段树的话，空间会炸！

那么我们想，由于整棵树是一棵二叉树，所以高度为 ${\log }_{2}N$ 左右，所以我们每次单点赋值只会更改最多 ${\log }_{2}N$ 左右的线段树节点！这句话就是主席树的关键。

所以针对每一次操作，我们只需保存新的被修改过的线段树节点就行了。

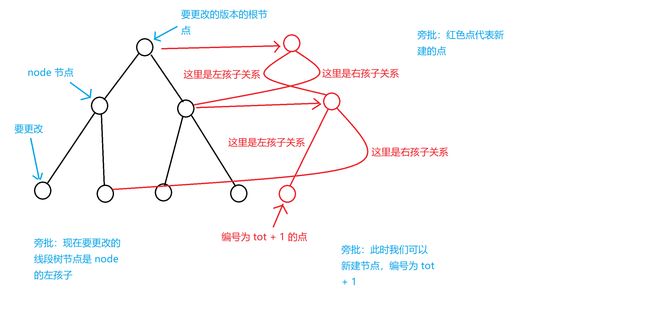
那么我们如何建这棵线段树呢？请看以下这个图：

我们可以看出，更新操作在原始版本上是不做任何修改的。我们只需要新建要修改的节点的副本，并且把副本的值一一改变，再与原始版本连边就可以了。

新建副本的意思就是，新建修改过后的节点，然后连边到要修改的历史版本的线段树里的没有修改过的节点（自己看图就清晰了）。

那么我们需要注意什么：

1. 主席树里有很多个版本，因此就会有很多的根节点，我们可以用数组 $root$ 来保存每个版本的根节点。

2. 每个节点有很多个父亲，但是永远只有两个儿子。

3. 由于编号的问题，所以我们必须要记录节点个数以此来进行编号。

4. 注意主席树里新建的点的左右儿子。

5. 由于是单点修改，所以不需要懒标记。

6. 在新建节点时，我们只需要把左右儿子分辨清楚就行了。

现在我们发现从任何一个根节点向下递归都是一棵线段树。

所以按照这个思路就可以开始打代码了。

这里我是把初始看成版本 $1$。

这里因为 $\text{pushup}$ 还是一样的操作，所以我就没有放上来了。

建树（$\text{build}$）

我们建树的时候可以先定义结构体 $segment\_tree$：

struct segment_tree
{
    int l, r;     //代表左右孩子
    int lt, rt;    //代表所表示的区间
    int val;      //代表节点的值
}tree[N * 4];

然后跟普通线段树一样的操作，只不过把 $roo{t}_1=1$。

void build(int node, int lt, int rt){
    if(lt == rt){
      tree[node].lt = lt, tree[node].rt = rt;
      tree[node].v = a[lt];   //这里由于是叶子节点所以左右儿子不用记
      return ;
    }
    int mid = lt + rt >> 1;
    tot = max(tot, node << 1 | 1);   //这里的 tot 表示的是节点总个数
    tree[node].lt = lt, tree[node].rt = rt;
    tree[node].l = node << 1, tree[node].r = node << 1 | 1;    //记录一下信息
    build(node << 1, lt, mid);
    build(node << 1 | 1, mid + 1, rt);
    pushup(node);
}

是不是很简单。

更新（$\text{update}$）

这里的更新先把代码放上来：

void update(int node, int x, int k){
    if(!tree[node].l && !tree[node].r){
        tot++;
        tree[tot].lt = tree[node].lt, tree[tot].rt = tree[node].rt;
        tree[tot].v = k;
        return ;
    }
    tot++;
    tree[tot].lt = tree[node].lt, tree[tot].rt = tree[node].rt;
    int tmp = tot;
    int mid = tree[node].lt + tree[node].rt >> 1;
    if(x <= mid){
        tree[tot].l = tot + 1, tree[tot].r = tree[node].r;
        update(tree[node].l, x, k);
    }
    else{
        tree[tot].l = tree[node].l, tree[tot].r = tot + 1;
        update(tree[node].r, x, k);
    }
}

然后解释是什么意思。

首先我们看 $8$ ~ $10$ 行，这里是新建一个节点。注意第 $10$ 行，我们先记一下 $tot$，为准备 $\text{pushup}$。

我们再看 $12$ ~ $15$ 行，这里的意思是 $x$ 在左儿子的区间内，所以结合图例我们可以看出：

我们发现，如果是这个节点的左节点要做修改，那么这个节点对应的新建的节点的左儿子就是接下来要新建的这个节点的左儿子节点的对应节点，我们可以算出编号为 $tot+1$，然后新建节点的右孩子还是对应节点的右孩子。

然后如果是修改右孩子直接反过来即可。

再来看 $2$ ~ $7$ 行，这里是到了叶子节点，我们还是新建一个节点，然后将权值设为 $k$。记得要 return ;

是不是很难？

查询（$\text{query}$）

查询的话，直接向下搜，搜到叶子节点直接返回就行了：

代码：

int query(int node, int x){
  if(!tree[node].l && !tree[node].r){
    return tree[node].v;
  }
  int mid = tree[node].lt + tree[node].rt >> 1;
  if(x <= mid){
    return query(tree[node].l, x);
  }
  else{
    return query(tree[node].r, x);
  }
  return 0;
}

这个很简单吧！注意只要从要求搜的 $root$ 就行了。

最后（空间复杂度分析）

注意，这里由于每次操作只更改 ${\log }_{2}N$ 个节点，所以只需要 $O(M{\log }_{2}N)$ 的空间就可以把所有历史版本的线段树全部记下来。

代码

代码就放上来吧：

#include

using namespace std;

inline int read() {    //注意这里时间会超，要开快读
	int x = 0, f = 1;
  char ch = getchar();
	while(ch < '0' || ch > '9'){
    if(ch == '-'){
      f = -1;
    }
    ch = getchar();
  }
	while(ch >= '0' && ch <= '9'){
    x = x * 10 + ch - 48;
    ch = getchar();
  }
	return x * f;
}

const int N = 1e6 + 5;
const int M = N * 26;

int n, m;
int a[N];

int tot;     //节点个数
int len, root[M];  //所有版本的根节点

struct segment_tree{
  int lt, rt;    //代表区间
  int l, r;   //左右孩子
  int v;    //代表值
}tree[M];

void pushup(int node){
  tree[node].v = tree[tree[node].l].v + tree[tree[node].r].v;
}

void build(int node, int lt, int rt){
  if(lt == rt){
    tree[node].lt = lt, tree[node].rt = rt;
    tree[node].v = a[lt];
    return ;
  }
  int mid = lt + rt >> 1;
  tot = max(tot, node << 1 | 1);
  tree[node].lt = lt, tree[node].rt = rt;
  tree[node].l = node << 1, tree[node].r = node << 1 | 1;
  build(node << 1, lt, mid);
  build(node << 1 | 1, mid + 1, rt);
}

void update(int node, int x, int k){
  if(!tree[node].l && !tree[node].r){
    tot++;
    tree[tot].lt = tree[node].lt, tree[tot].rt = tree[node].rt;
    tree[tot].v = k;
    return ;
  }
  tot++;
  tree[tot].lt = tree[node].lt, tree[tot].rt = tree[node].rt;
  int tmp = tot;
  int mid = tree[node].lt + tree[node].rt >> 1;
  if(x <= mid){
    tree[tot].l = tot + 1, tree[tot].r = tree[node].r;
    update(tree[node].l, x, k);
  }
  else{
    tree[tot].l = tree[node].l, tree[tot].r = tot + 1;
    update(tree[node].r, x, k);
  }
  pushup(tmp);
}

int query(int node, int x){
  if(!tree[node].l && !tree[node].r){
    return tree[node].v;
  }
  int mid = tree[node].lt + tree[node].rt >> 1;
  if(x <= mid){
    return query(tree[node].l, x);
  }
  else{
    return query(tree[node].r, x);
  }
  return 0;
}

void Solve(){
  n = read(), m = read();
  for(int i = 1; i <= n; i++){
    a[i] = read();
  }
  root[++len] = 1;
  build(1, 1, n);
  while(m--){
    int v, op;
    v = read(), op = read();
    v++;
    if(op == 1){
      int x, k;
      x = read(), k = read();
      root[++len] = tot + 1;
      update(root[v], x, k);    //注意从哪个版本开始找
    }
    else{
      int x;
      x = read();
      len++;
      root[len] = root[v];   //这里记一下版本根节点
      cout << query(root[v], x) << '\n';  //这里也一样
    }
  }
}

int main(){
  Solve();
  return 0;
}

疑问 & 催更

请私信 $\text{\_Alexande\_}$，这里有快速链接：$\text{Link}$。