三体攻击问题(三维数组的前缀和 与 差分)(上篇)
三体攻击问题
文章目录
- 三体攻击问题
-
- 题目详情
- 前言
- 预备知识【二维差分与前缀和】
- 三维前缀和
-
- 定义【官方解释】
- 自定义
-
- 三维数组求前缀和
- 三维差分
-
- 官方解释
- 自定义【跟二维差分类比】
- 三维查分的求解
- 总结
题目详情
三体人将对地球发起攻击。
为了抵御攻击,地球人派出了 A×B×C 艘战舰,在太空中排成一个 A 层 B 行 C 列的立方体。
其中,第 i层第 j 行第 k 列的战舰(记为战舰 (i,j,k))的生命值为 d(i,j,k)。
三体人将会对地球发起 m 轮“立方体攻击”,每次攻击会对一个小立方体中的所有战舰都造成相同的伤害。
具体地,第 t 轮攻击用 7 个参数 lat,rat,lbt,rbt,lct,rct,ht 描述;
所有满足 i∈[lat,rat],j∈[lbt,rbt],k∈[lct,rct] 的战舰 (i,j,k) 会受到 ht 的伤害。
如果一个战舰累计受到的总伤害超过其防御力,那么这个战舰会爆炸。
地球指挥官希望你能告诉他,第一艘爆炸的战舰是在哪一轮攻击后爆炸的。
输入格式
第一行包括 4 个正整数 A,B,C,m;
第二行包含 A×B×C 个整数,其中第 ((i−1)×B+(j−1))×C+(k−1)+1个数为 d(i, j, k)
第 3 到第 m+2行中,第 (t − 2) 行包含 7个正整数 lat, rat, lbt, rbt, lct, rct, ht。
输出格式
输出第一个爆炸的战舰是在哪一轮攻击后爆炸的。
保证一定存在这样的战舰。
数据范围
1≤A×B×C≤106
1≤m≤106
0≤d(i, j, k), ht≤109
1≤lat≤rat≤A
1≤lbt≤rbt≤B
1≤lct≤rct≤C
层、行、列的编号都从 1 开始。
输入样例:
2 2 2 3
1 1 1 1 1 1 1 1
1 2 1 2 1 1 1
1 1 1 2 1 2 1
1 1 1 1 1 1 2
输出样例:
2
样例解释
在第 2 轮攻击后,战舰 (1,1,1)总共受到了 2点伤害,超出其防御力导致爆炸。
前言
由于题目需要处理的信息量较大,所以文章分成两篇发布,本次将会介绍求解三维数组差分与前缀和的基本知识,【用 二维差分和前缀和 进行类比的手段】,下次将介绍题目的确切解法,喜欢的小伙伴可以点个关注。
预备知识【二维差分与前缀和】
这个可以查看我往期的博客链接,这里面附带了详细的教程: https://blog.csdn.net/2302_77698668/article/details/132767897
三维前缀和
定义【官方解释】
三维数组的前缀和是指对于一个三维数组,计算出每个位置(i, j, k)上的前缀和,即从原点(0, 0, 0)到位置(i, j, k)的所有元素的和。
具体计算方法如下:
-
创建一个与原数组相同大小的三维数组prefixSum,用于存储前缀和。
-
对于每个位置(i, j, k),计算其前缀和prefixSum[i][j][k],即从原点(0, 0, 0)到位置(i, j, k)的所有元素的和。
-
如果(i, j, k)是原数组的第一个元素,即(i, j, k) = (0, 0, 0),则prefixSum[i][j][k] = arr[i][j][k]。
-
否则,prefixSum[i][j][k] = arr[i][j][k] + prefixSum[i-1][j][k] + prefixSum[i][j-1][k] + prefixSum[i][j][k-1] - prefixSum[i-1][j-1][k] - prefixSum[i-1][j][k-1] - prefixSum[i][j-1][k-1] + prefixSum[i-1][j-1][k-1]。
-
-
最后,返回prefixSum作为结果。
以下是一个示例代码,用于计算三维数组的前缀和:
#include 注意:上述代码中,假设输入的三维数组arr的维度分别为n、m和p。在实际应用中,需要根据具体的情况进行修改。
自定义
三维数组求前缀和
上面的官方解释难免有些抽象,可能大家回想到一个正方体里面套着另外一个正方体的画面。这样就很难绷了,所以我会从二维的角度介绍。
定义,看图:
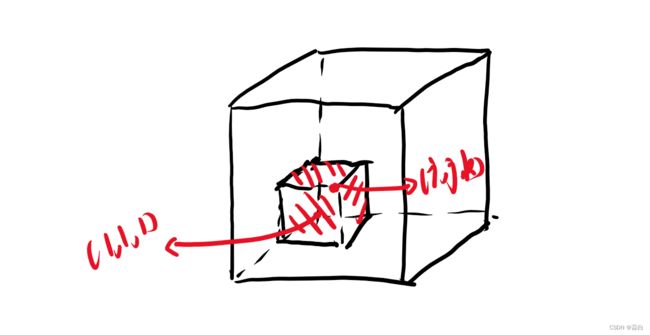
这上面的体积内包含的点所代表的值的总和就是前缀和
再看图,下图是将三维结构投影到二维的画面【顺便联想一下二维前缀和的画面】

这样的公式是不是和二维求前缀和比较像呢?
先处理平面,我们再来处理维度,对 k进行操作

我们再来处理红色标记的那一层平面,看图:

合起来的公式给大家写好:
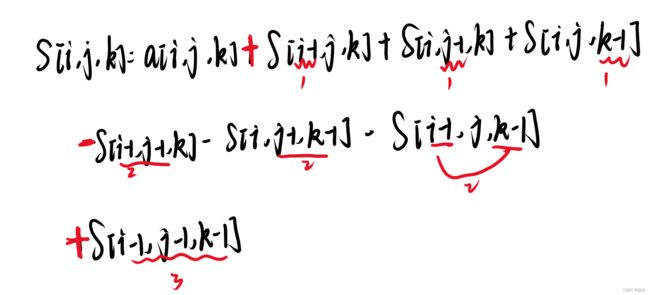
怎么样,发现规律了没有
有 1 个 -1 操作的是 +
有 2 个 -1 操作的是 -
有 3 个 -1 操作的是 +
这里的规律我用数组描述:
int d[8][4] = {
{0, 0, 0, 1},
{0, 0, 1, +1},
{0, 1, 0, +1},
{0, 1, 1, -1},
{1, 0, 0, +1},
{1, 0, 1, -1},
{1, 1, 0, -1},
{1, 1, 1, +1},
};
三维差分
官方解释
对于三维差分,我们可以使用前缀和来进行计算。前缀和是指对一个数组进行累加操作,得到一个新的数组,新数组的每个元素是原数组中前缀元素的总和。
以下是将三维差分应用于C++的示例代码:
#include 在上述代码中,我们定义了一个函数calculate3DDifference来计算三维差分。该函数接受一个三维数组作为输入,并返回一个新的三维数组,其中每个元素是原数组中相邻元素之差的累加和。在main函数中,我们调用calculate3DDifference函数来计算差分,并打印结果。
请注意,前缀和的计算需要考虑各种边界情况,以确保正确计算差分。在实际应用中,可能需要根据具体情况对边界元素进行处理。
自定义【跟二维差分类比】
假设我们有三维数组 a[N][N][N],对于每个 a [ i ] [ j ] [ k ]而言,我们都有个三维数组b [ N ] [N ] [N ],使得数组b [ i ] [ j ] [ k ]的前缀和对应的就是 a [ i ] [ j ] [k ]
三维查分的求解
下图跟之前的思路一样,记得联想二维差分的画面,【不记得的话可以观看前言链接中的博客】: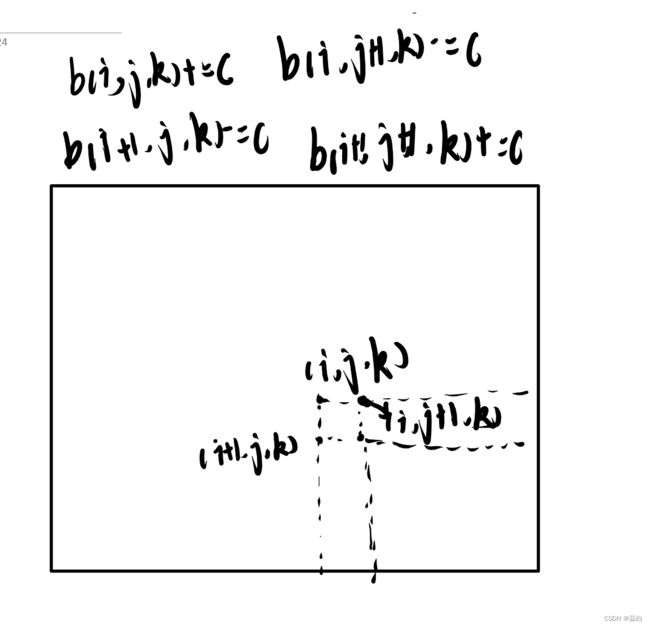
再对k + 1 层分析:
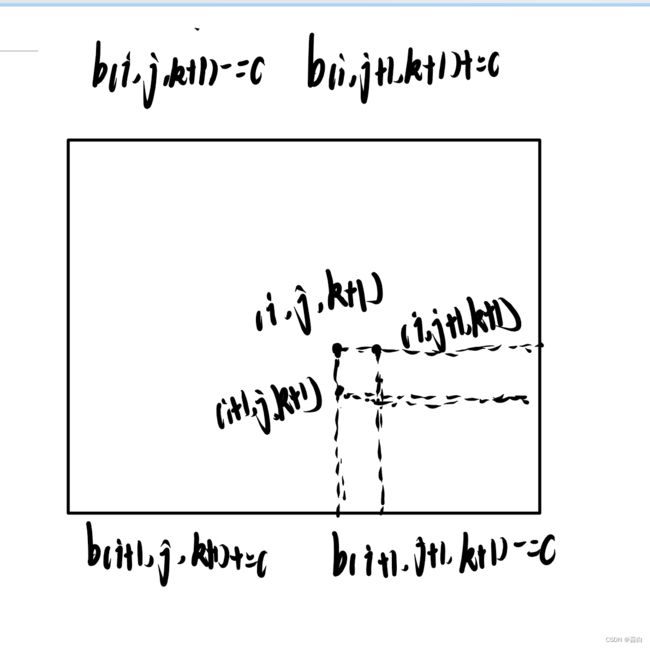
这里和之前一样,还是具有相同的规律:
有 1 个+1 操作–打补丁
有 2 个 +1操作–进行修改
。。。。。。。
总结
以上是公式推导操作,可以为后面的解题提供理论依据;下一篇文章将为大家带来题目的具体详解;