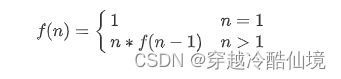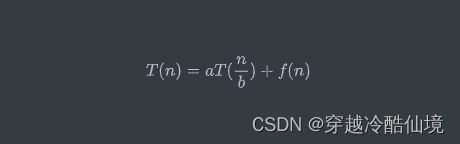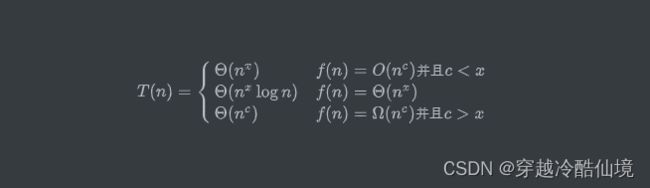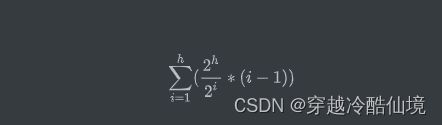穿越冷酷仙境
穿越冷酷仙境

基础数据结构

基础数据结构

1.数组

概述

定义

在计算机科学中，数组是由一组元素（值或变量）组成的数据结构，每个元素有至少一个索引或键来标识

因为数组内的元素是连续存储的，所以数组中元素的地址，可以通过其索引计算出来，例如：

int[] array = {1,2,3,4,5}

知道了数组的数据起始地址 $BaseAddress$，就可以由公式 $BaseAddress + i * size$ 计算出索引 $i$ 元素的地址

  • $i$ 即索引，在 Java、C 等语言都是从 0 开始

  • $size$ 是每个元素占用字节，例如 $int$ 占 $4$，$double$ 占 $8$

小测试

byte[] array = {1,2,3,4,5}

已知 array 的数据的起始地址是 0x7138f94c8，那么元素 3 的地址是什么？

答：0x7138f94c8 + 2 * 1 = 0x7138f94ca

空间占用  

Java 中数组结构为

  • 8 字节 markword

  • 4 字节 class 指针（压缩 class 指针的情况）

  • 4 字节 数组大小（决定了数组最大容量是 $2^{32}$）

  • 数组元素 + 对齐字节（java 中所有对象大小都是 8 字节的整数倍12，不足的要用对齐字节补足）

例如

int[] array = {1, 2, 3, 4, 5};

的大小为 40 个字节，组成如下

8 + 4 + 4 + 5*4 + 4(alignment)

随机访问性能

即根据索引查找元素，时间复杂度是 $O(1)$

动态数组

java 版本

public class DynamicArray implements Iterable {
    private int size = 0; // 逻辑大小
    private int capacity = 8; // 容量
    private int[] array = {};


    /**
     * 向最后位置 [size] 添加元素
     *
     * @param element 待添加元素
     */
    public void addLast(int element) {
        add(size, element);
    }

    /**
     * 向 [0 .. size] 位置添加元素
     *
     * @param index   索引位置
     * @param element 待添加元素
     */
    public void add(int index, int element) {
        checkAndGrow();

        // 添加逻辑
        if (index >= 0 && index < size) {
            // 向后挪动, 空出待插入位置
            System.arraycopy(array, index,
                    array, index + 1, size - index);
        }
        array[index] = element;
        size++;
    }

    private void checkAndGrow() {
        // 容量检查
        if (size == 0) {
            array = new int[capacity];
        } else if (size == capacity) {
            // 进行扩容, 1.5 1.618 2
            capacity += capacity >> 1;
            int[] newArray = new int[capacity];
            System.arraycopy(array, 0,
                    newArray, 0, size);
            array = newArray;
        }
    }

    /**
     * 从 [0 .. size) 范围删除元素
     *
     * @param index 索引位置
     * @return 被删除元素
     */
    public int remove(int index) { // [0..size)
        int removed = array[index];
        if (index < size - 1) {
            // 向前挪动
            System.arraycopy(array, index + 1,
                    array, index, size - index - 1);
        }
        size--;
        return removed;
    }


    /**
     * 查询元素
     *
     * @param index 索引位置, 在 [0..size) 区间内
     * @return 该索引位置的元素
     */
    public int get(int index) {
        return array[index];
    }

    /**
     * 遍历方法1
     *
     * @param consumer 遍历要执行的操作, 入参: 每个元素
     */
    public void foreach(Consumer consumer) {
        for (int i = 0; i < size; i++) {
            // 提供 array[i]
            // 返回 void
            consumer.accept(array[i]);
        }
    }

    /**
     * 遍历方法2 - 迭代器遍历
     */
    @Override
    public Iterator iterator() {
        return new Iterator() {
            int i = 0;

            @Override
            public boolean hasNext() { // 有没有下一个元素
                return i < size;
            }

            @Override
            public Integer next() { // 返回当前元素,并移动到下一个元素
                return array[i++];
            }
        };
    }

    /**
     * 遍历方法3 - stream 遍历
     *
     * @return stream 流
     */
    public IntStream stream() {
        return IntStream.of(Arrays.copyOfRange(array, 0, size));
    }
}

这些方法实现，都简化了 index 的有效性判断，假设输入的 index 都是合法的

插入或删除性能

头部位置，时间复杂度是 $O(n)$

中间位置，时间复杂度是 $O(n)$

尾部位置，时间复杂度是 $O(1)$（均摊来说）

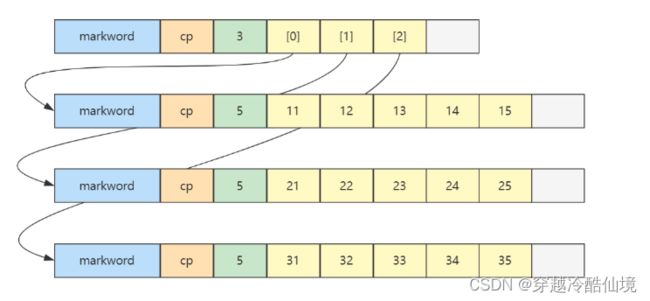
二维数组

int[][] array = {
    {11, 12, 13, 14, 15},
    {21, 22, 23, 24, 25},
    {31, 32, 33, 34, 35},
};

内存图如下

基础数据结构_第1张图片

  • 二维数组占 32 个字节，其中 array[0]，array[1]，array[2] 三个元素分别保存了指向三个一维数组的引用

  • 三个一维数组各占 40 个字节

  • 它们在内层布局上是连续的

更一般的，对一个二维数组 $Arraym$

  • $m$ 是外层数组的长度，可以看作 row 行

  • $n$ 是内层数组的长度，可以看作 column 列

  • 当访问 $Arrayi$，$0\leq i \lt m, 0\leq j \lt n$时，就相当于

    • 先找到第 $i$ 个内层数组（行）

    • 再找到此内层数组中第 $j$ 个元素（列)

小测试

Java 环境下（不考虑类指针和引用压缩，此为默认情况），有下面的二维数组

byte[][] array = {
    {11, 12, 13, 14, 15},
    {21, 22, 23, 24, 25},
    {31, 32, 33, 34, 35},
};

已知 array 对象起始地址是 0x1000，那么 23 这个元素的地址是什么？

答：

  • 起始地址 0x1000

  • 外层数组大小：16字节对象头 + 3元素 * 每个引用4字节 + 4 对齐字节 = 32 = 0x20

  • 第一个内层数组大小：16字节对象头 + 5元素 * 每个byte1字节 + 3 对齐字节 = 24 = 0x18

  • 第二个内层数组，16字节对象头 = 0x10，待查找元素索引为 2

  • 最后结果 = 0x1000 + 0x20 + 0x18 + 0x10 + 2*1 = 0x104a

局部性原理

这里只讨论空间局部性

  • cpu 读取内存（速度慢）数据后，会将其放入高速缓存（速度快）当中，如果后来的计算再用到此数据，在缓存中能读到的话，就不必读内存了

  • 缓存的最小存储单位是缓存行（cache line），一般是 64 bytes，一次读的数据少了不划算啊，因此最少读 64 bytes 填满一个缓存行，因此读入某个数据时也会读取其临近的数据，这就是所谓空间局部性

对效率的影响

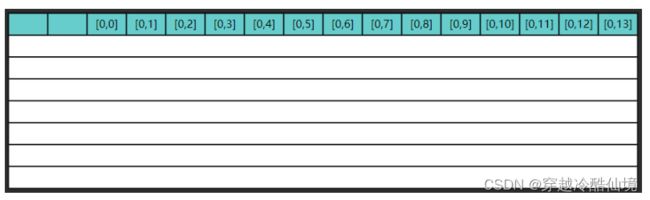
比较下面 ij 和 ji 两个方法的执行效率

int rows = 1000000;
int columns = 14;
int[][] a = new int[rows][columns];

StopWatch sw = new StopWatch();
sw.start("ij");
ij(a, rows, columns);
sw.stop();
sw.start("ji");
ji(a, rows, columns);
sw.stop();
System.out.println(sw.prettyPrint());

ij 方法

public static void ij(int[][] a, int rows, int columns) {
    long sum = 0L;
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < columns; j++) {
            sum += a[i][j];
        }
    }
    System.out.println(sum);
}

ji 方法

public static void ji(int[][] a, int rows, int columns) {
    long sum = 0L;
    for (int j = 0; j < columns; j++) {
        for (int i = 0; i < rows; i++) {
            sum += a[i][j];
        }
    }
    System.out.println(sum);
}

执行结果

0
0
StopWatch '': running time = 96283300 ns
---------------------------------------------
ns         %     Task name
---------------------------------------------
016196200  017%  ij
080087100  083%  ji

可以看到 ij 的效率比 ji 快很多，为什么呢？

  • 缓存是有限的，当新数据来了后，一些旧的缓存行数据就会被覆盖

  • 如果不能充分利用缓存的数据，就会造成效率低下

以 ji 执行为例，第一次内循环要读入 $[0,0]$ 这条数据，由于局部性原理，读入 $[0,0]$ 的同时也读入了 $[0,1] ... [0,13]$，如图所示

基础数据结构_第2张图片

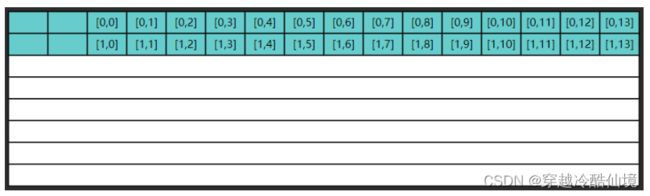
 但很遗憾，第二次内循环要的是 $[1,0]$ 这条数据，缓存中没有，于是再读入了下图的数据

基础数据结构_第3张图片

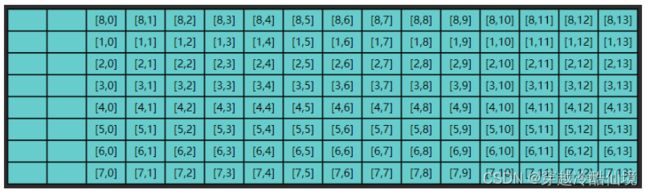
 这显然是一种浪费，因为 $[0,1] ... [0,13]$ 包括 $[1,1] ... [1,13]$ 这些数据虽然读入了缓存，却没有及时用上，而缓存的大小是有限的，等执行到第九次内循环时

基础数据结构_第4张图片

缓存的第一行数据已经被新的数据 $[8,0] ... [8,13]$ 覆盖掉了，以后如果再想读，比如 $[0,1]$，又得到内存去读了

同理可以分析 ij 函数则能充分利用局部性原理加载到的缓存数据

举一反三

  1. I/O 读写时同样可以体现局部性原理

  2. 数组可以充分利用局部性原理，那么链表呢？

    答：链表不行，因为链表的元素并非相邻存储

越界检查

java 中对数组元素的读写都有越界检查，类似于下面的代码

bool is_within_bounds(int index) const        
{ 
    return 0 <= index && index < length(); 
}

  • 代码位置：openjdk\src\hotspot\share\oops\arrayOop.hpp

只不过此检查代码，不需要由程序员自己来调用，JVM 会帮我们调用

2. 链表

概述

定义

在计算机科学中，链表是数据元素的线性集合，其每个元素都指向下一个元素，元素存储上并不连续

可以分类为

单向链表，每个元素只知道其下一个元素是谁

双向链表，每个元素知道其上一个元素和下一个元素

循环链表，通常的链表尾节点 tail 指向的都是 null，而循环链表的 tail 指向的是头节点 head

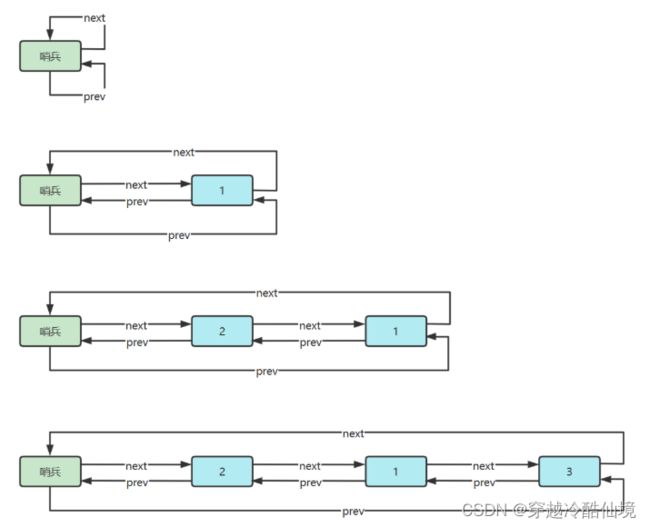
链表内还有一种特殊的节点称为哨兵（Sentinel）节点，也叫做哑元（ Dummy）节点，它不存储数据，通常用作头尾，用来简化边界判断，如下图所示

随机访问性能

根据 index 查找，时间复杂度 $O(n)$

插入或删除性能

  • 起始位置：$O(1)$

  • 结束位置：如果已知 tail 尾节点是 $O(1)$，不知道 tail 尾节点是 $O(n)$

  • 中间位置：根据 index 查找时间 + $O(1)$

单向链表

根据单向链表的定义，首先定义一个存储 value 和 next 指针的类 Node，和一个描述头部节点的引用

public class SinglyLinkedList {
    
    private Node head; // 头部节点
    
    private static class Node { // 节点类
        int value;
        Node next;

        public Node(int value, Node next) {
            this.value = value;
            this.next = next;
        }
    }
}

  • Node 定义为内部类，是为了对外隐藏实现细节，没必要让类的使用者关心 Node 结构

  • 定义为 static 内部类，是因为 Node 不需要与 SinglyLinkedList 实例相关，多个 SinglyLinkedList实例能共用 Node 类定义

头部添加

public class SinglyLinkedList {
    // ...
    public void addFirst(int value) {
		this.head = new Node(value, this.head);
    }
}

  • 如果 this.head == null，新增节点指向 null，并作为新的 this.head

  • 如果 this.head != null，新增节点指向原来的 this.head，并作为新的 this.head

    • 注意赋值操作执行顺序是从右到左

while 遍历

public class SinglyLinkedList {
    // ...
    public void loop() {
        for (Node curr = this.head; curr != null; curr = curr.next) {
            // 做一些事
        }
    }
}

以上两种遍历都可以把要做的事以 Consumer 函数的方式传递进来

  • Consumer 的规则是一个参数，无返回值，因此像 System.out::println 方法等都是 Consumer

  • 调用 Consumer 时，将当前节点 curr.value 作为参数传递给它

迭代器遍历

public class SinglyLinkedList implements Iterable {
    // ...
    private class NodeIterator implements Iterator {
        Node curr = head;
        
        public boolean hasNext() {
            return curr != null;
        }

        public Integer next() {
            int value = curr.value;
            curr = curr.next;
            return value;
        }
    }
    
    public Iterator iterator() {
        return new NodeIterator();
    }
}

  • hasNext 用来判断是否还有必要调用 next

  • next 做两件事

    • 返回当前节点的 value

    • 指向下一个节点

  • NodeIterator 要定义为非 static 内部类，是因为它与 SinglyLinkedList 实例相关，是对某个 SinglyLinkedList 实例的迭代

递归遍历  

public class SinglyLinkedList implements Iterable {
    // ...
    public void loop() {
        recursion(this.head);
    }

    private void recursion(Node curr) {
        if (curr == null) {
            return;
        }
        // 前面做些事
        recursion(curr.next);
        // 后面做些事
    }
}

尾部添加

public class SinglyLinkedList {
    // ...
    private Node findLast() {
        if (this.head == null) {
            return null;
        }
        Node curr;
        for (curr = this.head; curr.next != null; ) {
            curr = curr.next;
        }
        return curr;
    }
    
    public void addLast(int value) {
        Node last = findLast();
        if (last == null) {
            addFirst(value);
            return;
        }
        last.next = new Node(value, null);
    }
}

  • 注意，找最后一个节点，终止条件是 curr.next == null

  • 分成两个方法是为了代码清晰，而且 findLast() 之后还能复用

尾部添加多个

public class SinglyLinkedList {
    // ...
	public void addLast(int first, int... rest) {
        
        Node sublist = new Node(first, null);
        Node curr = sublist;
        for (int value : rest) {
            curr.next = new Node(value, null);
            curr = curr.next;
        }
        
        Node last = findLast();
        if (last == null) {
            this.head = sublist;
            return;
        }
        last.next = sublist;
    }
}

  • 先串成一串 sublist

  • 再作为一个整体添加

根据索引获取

public class SinglyLinkedList {
    // ...
	private Node findNode(int index) {
        int i = 0;
        for (Node curr = this.head; curr != null; curr = curr.next, i++) {
            if (index == i) {
                return curr;
            }
        }
        return null;
    }
    
    private IllegalArgumentException illegalIndex(int index) {
        return new IllegalArgumentException(String.format("index [%d] 不合法%n", index));
    }
    
    public int get(int index) {
        Node node = findNode(index);
        if (node != null) {
            return node.value;
        }
        throw illegalIndex(index);
    }
}

同样，分方法可以实现复用

插入

public class SinglyLinkedList {
    // ...
	public void insert(int index, int value) {
        if (index == 0) {
            addFirst(value);
            return;
        }
        Node prev = findNode(index - 1); // 找到上一个节点
        if (prev == null) { // 找不到
            throw illegalIndex(index);
        }
        prev.next = new Node(value, prev.next);
    }
}

插入包括下面的删除，都必须找到上一个节点

删除

public class SinglyLinkedList {
    // ...
	public void remove(int index) {
        if (index == 0) {
            if (this.head != null) {
                this.head = this.head.next;
                return;
            } else {
                throw illegalIndex(index);
            }
        }
        Node prev = findNode(index - 1);
        Node curr;
        if (prev != null && (curr = prev.next) != null) {
            prev.next = curr.next;
        } else {
            throw illegalIndex(index);
        }
    }
}

  • 第一个 if 块对应着 removeFirst 情况

  • 最后一个 if 块对应着至少得两个节点的情况

    • 不仅仅判断上一个节点非空，还要保证当前节点非空

单向链表（带哨兵）

观察之前单向链表的实现，发现每个方法内几乎都有判断是不是 head 这样的代码，能不能简化呢？

用一个不参与数据存储的特殊 Node 作为哨兵，它一般被称为哨兵或哑元，拥有哨兵节点的链表称为带头链表

public class SinglyLinkedListSentinel {
    // ...
    private Node head = new Node(Integer.MIN_VALUE, null);
}

  • 具体存什么值无所谓，因为不会用到它的值

加入哨兵节点后，代码会变得比较简单，先看几个工具方法

public class SinglyLinkedListSentinel {
    // ...
    
    // 根据索引获取节点
    private Node findNode(int index) {
        int i = -1;
        for (Node curr = this.head; curr != null; curr = curr.next, i++) {
            if (i == index) {
                return curr;
            }
        }
        return null;
    }
    
    // 获取最后一个节点
    private Node findLast() {
        Node curr;
        for (curr = this.head; curr.next != null; ) {
            curr = curr.next;
        }
        return curr;
    }
}

  • findNode 与之前类似，只是 i 初始值设置为 -1 对应哨兵，实际传入的 index 也是 $[-1, \infty)$

  • findLast 绝不会返回 null 了，就算没有其它节点，也会返回哨兵作为最后一个节点

这样，代码简化为

public class SinglyLinkedListSentinel {
    // ...
    
    public void addLast(int value) {
        Node last = findLast();
        /*
        改动前
        if (last == null) {
            this.head = new Node(value, null);
            return;
        }
        */
        last.next = new Node(value, null);
    }
    
    public void insert(int index, int value) {
        /*
        改动前
        if (index == 0) {
            this.head = new Node(value, this.head);
            return;
        }
        */
        // index 传入 0 时，返回的是哨兵
        Node prev = findNode(index - 1);
        if (prev != null) {
            prev.next = new Node(value, prev.next);
        } else {
            throw illegalIndex(index);
        }
    }
    
    public void remove(int index) {
        /*
        改动前
        if (index == 0) {
            if (this.head != null) {
                this.head = this.head.next;
                return;
            } else {
                throw illegalIndex(index);
            }
        }
        */
        // index 传入 0 时，返回的是哨兵
        Node prev = findNode(index - 1);
        Node curr;
        if (prev != null && (curr = prev.next) != null) {
            prev.next = curr.next;
        } else {
            throw illegalIndex(index);
        }
    }
    
    public void addFirst(int value) {
        /*
        改动前
        this.head = new Node(value, this.head);
        */
		this.head.next = new Node(value, this.head.next);
        // 也可以视为 insert 的特例, 即 insert(0, value);
    }
}

对于删除，前面说了【最后一个 if 块对应着至少得两个节点的情况】，现在有了哨兵，就凑足了两个节点

双向链表（带哨兵）

public class DoublyLinkedListSentinel implements Iterable {

    private final Node head;
    private final Node tail;

    public DoublyLinkedListSentinel() {
        head = new Node(null, 666, null);
        tail = new Node(null, 888, null);
        head.next = tail;
        tail.prev = head;
    }

    private Node findNode(int index) {
        int i = -1;
        for (Node p = head; p != tail; p = p.next, i++) {
            if (i == index) {
                return p;
            }
        }
        return null;
    }

    public void addFirst(int value) {
        insert(0, value);
    }

    public void removeFirst() {
        remove(0);
    }

    public void addLast(int value) {
        Node prev = tail.prev;
        Node added = new Node(prev, value, tail);
        prev.next = added;
        tail.prev = added;
    }

    public void removeLast() {
        Node removed = tail.prev;
        if (removed == head) {
            throw illegalIndex(0);
        }
        Node prev = removed.prev;
        prev.next = tail;
        tail.prev = prev;
    }

    public void insert(int index, int value) {
        Node prev = findNode(index - 1);
        if (prev == null) {
            throw illegalIndex(index);
        }
        Node next = prev.next;
        Node inserted = new Node(prev, value, next);
        prev.next = inserted;
        next.prev = inserted;
    }

    public void remove(int index) {
        Node prev = findNode(index - 1);
        if (prev == null) {
            throw illegalIndex(index);
        }
        Node removed = prev.next;
        if (removed == tail) {
            throw illegalIndex(index);
        }
        Node next = removed.next;
        prev.next = next;
        next.prev = prev;
    }

    private IllegalArgumentException illegalIndex(int index) {
        return new IllegalArgumentException(
                String.format("index [%d] 不合法%n", index));
    }

    @Override
    public Iterator iterator() {
        return new Iterator() {
            Node p = head.next;

            @Override
            public boolean hasNext() {
                return p != tail;
            }

            @Override
            public Integer next() {
                int value = p.value;
                p = p.next;
                return value;
            }
        };
    }

    static class Node {
        Node prev;
        int value;
        Node next;

        public Node(Node prev, int value, Node next) {
            this.prev = prev;
            this.value = value;
            this.next = next;
        }
    }
}

环形链表（带哨兵）

双向环形链表带哨兵，这时哨兵既作为头，也作为尾

基础数据结构_第5张图片

参考实现  

public class DoublyLinkedListSentinel implements Iterable {

    @Override
    public Iterator iterator() {
        return new Iterator<>() {
            Node p = sentinel.next;

            @Override
            public boolean hasNext() {
                return p != sentinel;
            }

            @Override
            public Integer next() {
                int value = p.value;
                p = p.next;
                return value;
            }
        };
    }

    static class Node {
        Node prev;
        int value;
        Node next;

        public Node(Node prev, int value, Node next) {
            this.prev = prev;
            this.value = value;
            this.next = next;
        }
    }

    private final Node sentinel = new Node(null, -1, null); // 哨兵

    public DoublyLinkedListSentinel() {
        sentinel.next = sentinel;
        sentinel.prev = sentinel;
    }

    /**
     * 添加到第一个
     * @param value 待添加值
     */
    public void addFirst(int value) {
        Node next = sentinel.next;
        Node prev = sentinel;
        Node added = new Node(prev, value, next);
        prev.next = added;
        next.prev = added;
    }

    /**
     * 添加到最后一个
     * @param value 待添加值
     */
    public void addLast(int value) {
        Node prev = sentinel.prev;
        Node next = sentinel;
        Node added = new Node(prev, value, next);
        prev.next = added;
        next.prev = added;
    }
    
    /**
     * 删除第一个
     */
    public void removeFirst() {
        Node removed = sentinel.next;
        if (removed == sentinel) {
            throw new IllegalArgumentException("非法");
        }
        Node a = sentinel;
        Node b = removed.next;
        a.next = b;
        b.prev = a;
    }

    /**
     * 删除最后一个
     */
    public void removeLast() {
        Node removed = sentinel.prev;
        if (removed == sentinel) {
            throw new IllegalArgumentException("非法");
        }
        Node a = removed.prev;
        Node b = sentinel;
        a.next = b;
        b.prev = a;
    }

    /**
     * 根据值删除节点
     * 
假定 value 在链表中作为 key, 有唯一性

     * @param value 待删除值
     */
    public void removeByValue(int value) {
        Node removed = findNodeByValue(value);
        if (removed != null) {
            Node prev = removed.prev;
            Node next = removed.next;
            prev.next = next;
            next.prev = prev;
        }
    }

    private Node findNodeByValue(int value) {
        Node p = sentinel.next;
        while (p != sentinel) {
            if (p.value == value) {
                return p;
            }
            p = p.next;
        }
        return null;
    }

}

3. 递归

概述

定义

计算机科学中，递归是一种解决计算问题的方法，其中解决方案取决于同一类问题的更小子集

比如单链表递归遍历的例子：

void f(Node node) {
    if(node == null) {
        return;
    }
    println("before:" + node.value)
    f(node.next);
    println("after:" + node.value)
}

说明：

  1. 自己调用自己，如果说每个函数对应着一种解决方案，自己调用自己意味着解决方案是一样的（有规律的）

  2. 每次调用，函数处理的数据会较上次缩减（子集），而且最后会缩减至无需继续递归

  3. 内层函数调用（子集处理）完成，外层函数才能算调用完成

原理

假设链表中有 3 个节点，value 分别为 1，2，3，以上代码的执行流程就类似于下面的伪码

// 1 -> 2 -> 3 -> null  f(1)

void f(Node node = 1) {
    println("before:" + node.value) // 1
    void f(Node node = 2) {
        println("before:" + node.value) // 2
        void f(Node node = 3) {
            println("before:" + node.value) // 3
            void f(Node node = null) {
                if(node == null) {
                    return;
                }
            }
            println("after:" + node.value) // 3
        }
        println("after:" + node.value) // 2
    }
    println("after:" + node.value) // 1
}

思路

  1. 确定能否使用递归求解

  2. 推导出递推关系，即父问题与子问题的关系，以及递归的结束条件

例如之前遍历链表的递推关系为

  • 深入到最里层叫做递

  • 从最里层出来叫做归

  • 在递的过程中，外层函数内的局部变量（以及方法参数）并未消失，归的时候还可以用到

单路递归 Single Recursion

E01. 阶乘

用递归方法求阶乘

  • 阶乘的定义 $n!= 1⋅2⋅3⋯(n-2)⋅(n-1)⋅n$，其中 $n$ 为自然数，当然 $0! = 1$

  • 递推关系

代码

private static int f(int n) {
    if (n == 1) {
        return 1;
    }
    return n * f(n - 1);
}

 拆解伪码如下，假设 n 初始值为 3

f(int n = 3) { // 解决不了,递
    return 3 * f(int n = 2) { // 解决不了,继续递
        return 2 * f(int n = 1) {
            if (n == 1) { // 可以解决, 开始归
                return 1;
            }
        }
    }
}

E02. 反向打印字符串

用递归反向打印字符串，n 为字符在整个字符串 str 中的索引位置

  • 递：n 从 0 开始，每次 n + 1，一直递到 n == str.length() - 1

  • 归：从 n == str.length() 开始归，从归打印，自然是逆序的

递推关系

代码为

public static void reversePrint(String str, int index) {
    if (index == str.length()) {
        return;
    }
    reversePrint(str, index + 1);
    System.out.println(str.charAt(index));
}

 拆解伪码如下，假设字符串为 "abc"

void reversePrint(String str, int index = 0) {
    void reversePrint(String str, int index = 1) {
        void reversePrint(String str, int index = 2) {
            void reversePrint(String str, int index = 3) { 
                if (index == str.length()) {
                    return; // 开始归
                }
            }
            System.out.println(str.charAt(index)); // 打印 c
        }
        System.out.println(str.charAt(index)); // 打印 b
    }
    System.out.println(str.charAt(index)); // 打印 a
}

多路递归 Multi Recursion

E01. 斐波那契数列

  • 之前的例子是每个递归函数只包含一个自身的调用，这称之为 single recursion

  • 如果每个递归函数例包含多个自身调用，称之为 multi recursion

递推关系

下面的表格列出了数列的前几项

 

实现

public static int f(int n) {
    if (n == 0) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
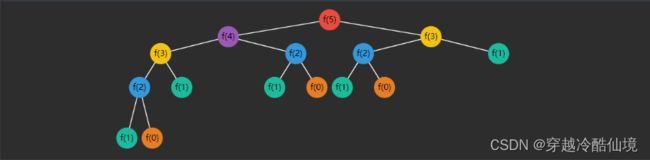
    return f(n - 1) + f(n - 2);
}

 

时间复杂度

  • 递归的次数也符合斐波那契规律，$2 * f(n+1)-1$

  • 时间复杂度推导过程

    • 斐波那契通项公式 $f(n) = \frac{1}{\sqrt{5}}*({\frac{1+\sqrt{5}}{2}}^n - {\frac{1-\sqrt{5}}{2}}^n)$

    • 简化为：$f(n) = \frac{1}{2.236}*({1.618}^n - {(-0.618)}^n)$

    • 带入递归次数公式 $2\frac{1}{2.236}({1.618}^{n+1} - {(-0.618)}^{n+1})-1$

    • 时间复杂度为 $\Theta(1.618^n)$

  1. 更多 Fibonacci 参考8910

  2. 以上时间复杂度分析，未考虑大数相加的因素

变体1 - 兔子问题8  

基础数据结构_第6张图片

  • 第一个月，有一对未成熟的兔子（黑色，注意图中个头较小）

  • 第二个月，它们成熟

  • 第三个月，它们能产下一对新的小兔子（蓝色）

  • 所有兔子遵循相同规律，求第 $n$ 个月的兔子数

分析

兔子问题如何与斐波那契联系起来呢？设第 n 个月兔子数为 $f(n)$

  • $f(n)$ = 上个月兔子数 + 新生的小兔子数

  • 而【新生的小兔子数】实际就是【上个月成熟的兔子数】

  • 因为需要一个月兔子就成熟，所以【上个月成熟的兔子数】也就是【上上个月的兔子数】

  • 上个月兔子数，即 $f(n-1)$

  • 上上个月的兔子数，即 $f(n-2)$

因此本质还是斐波那契数列，只是从其第一项开始

变体2 - 青蛙爬楼梯

  • 楼梯有 $n$ 阶

  • 青蛙要爬到楼顶，可以一次跳一阶，也可以一次跳两阶

  • 只能向上跳，问有多少种跳法

分析

n        跳法 规律
1 (1) 暂时看不出
 
2 (1,1) (2) 暂时看不出
3 (1,1,1) (1,2) (2,1) 暂时看不出
4 (1,1,1,1) (1,2,1) (2,1,1) (1,1,2) (2,2) 最后一跳，跳一个台阶的，基于f(3) 最后一跳，跳两个台阶的，基于f(2)
5 ... ...

 

  • 因此本质上还是斐波那契数列，只是从其第二项开始

  • 对应 leetcode 题目 70. 爬楼梯 - 力扣（LeetCode）

递归优化-记忆法

基础数据结构_第7张图片

可以看到（颜色相同的是重复的）：

  • $f(3)$ 重复了 2 次

  • $f(2)$ 重复了 3 次

  • $f(1)$ 重复了 5 次

  • $f(0)$ 重复了 3 次

随着 $n$ 的增大，重复次数非常可观，如何优化呢？

Memoization 记忆法（也称备忘录）是一种优化技术，通过存储函数调用结果（通常比较昂贵），当再次出现相同的输入（子问题）时，就能实现加速效果，改进后的代码  

public static void main(String[] args) {
    int n = 13;
    int[] cache = new int[n + 1];
    Arrays.fill(cache, -1);
    cache[0] = 0;
    cache[1] = 1;
    System.out.println(f(cache, n));
}

public static int f(int[] cache, int n) {
    if (cache[n] != -1) {
        return cache[n];
    }

    cache[n] = f(cache, n - 1) + f(cache, n - 2);
    return cache[n];
}

优化后的图示，只要结果被缓存，就不会执行其子问题

基础数据结构_第8张图片

 

  • 改进后的时间复杂度为 $O(n)$

  • 请自行验证改进后的效果

  • 请自行分析改进后的空间复杂度

注意

  1. 记忆法是动态规划的一种情况，强调的是自顶向下的解决

  2. 记忆法的本质是空间换时间

递归优化-尾递归

爆栈

用递归做 $n + (n-1) + (n-2) ... + 1$

public static long sum(long n) {
    if (n == 1) {
        return 1;
    }
    return n + sum(n - 1);
}

 在我的机器上 $n = 12000$ 时，爆栈了

Exception in thread "main" java.lang.StackOverflowError
	at Test.sum(Test.java:10)
	at Test.sum(Test.java:10)
	at Test.sum(Test.java:10)
	at Test.sum(Test.java:10)
	at Test.sum(Test.java:10)
	...

为什么呢？

  • 每次方法调用是需要消耗一定的栈内存的，这些内存用来存储方法参数、方法内局部变量、返回地址等等

  • 方法调用占用的内存需要等到方法结束时才会释放

  • 而递归调用我们之前讲过，不到最深不会回头，最内层方法没完成之前，外层方法都结束不了

    • 例如，$sum(3)$ 这个方法内有个需要执行 $3 + sum(2)$，$sum(2)$ 没返回前，加号前面的 $3$ 不能释放

    • 看下面伪码

long sum(long n = 3) {
    return 3 + long sum(long n = 2) {
        return 2 + long sum(long n = 1) {
            return 1;
        }
    }
}

尾调用

如果函数的最后一步是调用一个函数，那么称为尾调用，例如

function a() {
    return b()
}

下面三段代码不能叫做尾调用

function a() {
    const c = b()
    return c
}

因为最后一步并非调用函数

function a() {
    return b() + 1
}

最后一步执行的是加法

function a(x) {
    return b() + x
}

最后一步执行的是加法

一些语言11的编译器能够对尾调用做优化，例如

function a() {
    // 做前面的事
    return b() 
}

function b() {
    // 做前面的事
    return c()
}

function c() {
    return 1000
}

a()

没优化之前的伪码

function a() {
    return function b() {
        return function c() {
            return 1000
        }
    }
}

优化后伪码如下

a()
b()
c()

为何尾递归才能优化？

调用 a 时

  • a 返回时发现：没什么可留给 b 的，将来返回的结果 b 提供就可以了，用不着我 a 了，我的内存就可以释放

调用 b 时

  • b 返回时发现：没什么可留给 c 的，将来返回的结果 c 提供就可以了，用不着我 b 了，我的内存就可以释放

如果调用 a 时

  • 不是尾调用，例如 return b() + 1，那么 a 就不能提前结束，因为它还得利用 b 的结果做加法

尾递归

尾递归是尾调用的一种特例，也就是最后一步执行的是同一个函数

尾递归避免爆栈

安装 Scala

基础数据结构_第9张图片

Scala 入门

object Main {
  def main(args: Array[String]): Unit = {
    println("Hello Scala")
  }
}

 

  • Scala 是 java 的近亲，java 中的类都可以拿来重用

  • 类型是放在变量后面的

  • Unit 表示无返回值，类似于 void

  • 不需要以分号作为结尾，当然加上也对

还是先写一个会爆栈的函数

def sum(n: Long): Long = {
    if (n == 1) {
        return 1
    }
    return n + sum(n - 1)
}

Scala 最后一行代码若作为返回值，可以省略 return

不出所料，在 $n = 11000$ 时，还是出了异常

println(sum(11000))

Exception in thread "main" java.lang.StackOverflowError
	at Main$.sum(Main.scala:25)
	at Main$.sum(Main.scala:25)
	at Main$.sum(Main.scala:25)
	at Main$.sum(Main.scala:25)
	...

这是因为以上代码，还不是尾调用，要想成为尾调用，那么：

  1. 最后一行代码，必须是一次函数调用

  2. 内层函数必须摆脱与外层函数的关系，内层函数执行后不依赖于外层的变量或常量

def sum(n: Long): Long = {
    if (n == 1) {
        return 1
    }
    return n + sum(n - 1)  // 依赖于外层函数的 n 变量
}

如何让它执行后就摆脱对 n 的依赖呢？

  • 不能等递归回来再做加法，那样就必须保留外层的 n

  • 把 n 当做内层函数的一个参数传进去，这时 n 就属于内层函数了

  • 传参时就完成累加, 不必等回来时累加

sum(n - 1, n + 累加器)

改写后代码如下

@tailrec
def sum(n: Long, accumulator: Long): Long = {
    if (n == 1) {
        return 1 + accumulator
    } 
    return sum(n - 1, n + accumulator)
}

  • accumulator 作为累加器

  • @tailrec 注解是 scala 提供的，用来检查方法是否符合尾递归

  • 这回 sum(10000000, 0) 也没有问题，打印 50000005000000

执行流程如下，以伪码表示 $sum(4, 0)$

// 首次调用
def sum(n = 4, accumulator = 0): Long = {
    return sum(4 - 1, 4 + accumulator)
}

// 接下来调用内层 sum, 传参时就完成了累加, 不必等回来时累加，当内层 sum 调用后，外层 sum 空间没必要保留
def sum(n = 3, accumulator = 4): Long = {
    return sum(3 - 1, 3 + accumulator)
}

// 继续调用内层 sum
def sum(n = 2, accumulator = 7): Long = {
    return sum(2 - 1, 2 + accumulator)
}

// 继续调用内层 sum, 这是最后的 sum 调用完就返回最后结果 10, 前面所有其它 sum 的空间早已释放
def sum(n = 1, accumulator = 9): Long = {
    if (1 == 1) {
        return 1 + accumulator
    }
}

本质上，尾递归优化是将函数的递归调用，变成了函数的循环调用

改循环避免爆栈

public static void main(String[] args) {
    long n = 100000000;
    long sum = 0;
    for (long i = n; i >= 1; i--) {
        sum += i;
    }
    System.out.println(sum);
}

递归时间复杂度-Master theorem14

若有递归式

基础数据结构_第10张图片

其中

  • $T(n)$ 是问题的运行时间，$n$ 是数据规模

  • $a$ 是子问题个数

  • $T(\frac{n}{b})$ 是子问题运行时间，每个子问题被拆成原问题数据规模的 $\frac{n}{b}$

  • $f(n)$ 是除递归外执行的计算

令 $x = \log{b}{a}$，即 $x = \log{子问题缩小倍数}{子问题个数}$

那么

基础数据结构_第11张图片

例1

$T(n) = 2T(\frac{n}{2}) + n^4$

  • 此时 $x = 1 < 4$，由后者决定整个时间复杂度 $\Theta(n^4)$

  • 如果觉得对数不好算，可以换为求【$b$ 的几次方能等于 $a$】

例2

$T(n) = T(\frac{7n}{10}) + n$

  • $a=1, b=\frac{10}{7}, x=0, c=1$

  • 此时 $x = 0 < 1$，由后者决定整个时间复杂度 $\Theta(n)$

例3

$T(n) = 16T(\frac{n}{4}) + n^2$

  • $a=16, b=4, x=2, c=2$

  • 此时 $x=2 = c$，时间复杂度 $\Theta(n^2 \log{n})$

例4

$T(n)=7T(\frac{n}{3}) + n^2$

  • $a=7, b=3, x=1.?, c=2$

  • 此时 $x = \log_{3}{7} < 2$，由后者决定整个时间复杂度 $\Theta(n^2)$

 

例5

$T(n) = 7T(\frac{n}{2}) + n^2$

  • $a=7, b=2, x=2.?, c=2$

  • 此时 $x = log_2{7} > 2$，由前者决定整个时间复杂度 $\Theta(n^{\log_2{7}})$

例6

$T(n) = 2T(\frac{n}{4}) + \sqrt{n}$

  • $a=2, b=4, x = 0.5, c=0.5$

  • 此时 $x = 0.5 = c$，时间复杂度 $\Theta(\sqrt{n}\ \log{n})$

例7. 二分查找递归

int f(int[] a, int target, int i, int j) {
    if (i > j) {
        return -1;
    }
    int m = (i + j) >>> 1;
    if (target < a[m]) {
        return f(a, target, i, m - 1);
    } else if (a[m] < target) {
        return f(a, target, m + 1, j);
    } else {
        return m;
    }
}

 

  • 子问题个数 $a = 1$

  • 子问题数据规模缩小倍数 $b = 2$

  • 除递归外执行的计算是常数级 $c=0$

$T(n) = T(\frac{n}{2}) + n^0$

  • 此时 $x=0 = c$，时间复杂度 $\Theta(\log{n})$

例8. 归并排序递归

void split(B[], i, j, A[])
{
    if (j - i <= 1)                    
        return;                                
    m = (i + j) / 2;             
    
    // 递归
    split(A, i, m, B);  
    split(A, m, j, B); 
    
    // 合并
    merge(B, i, m, j, A);
}

  • 子问题个数 $a=2$

  • 子问题数据规模缩小倍数 $b=2$

  • 除递归外，主要时间花在合并上，它可以用 $f(n) = n$ 表示

$T(n) = 2T(\frac{n}{2}) + n$

  • 此时 $x=1=c$，时间复杂度 $\Theta(n\log{n})$

例9. 快速排序递归

algorithm quicksort(A, lo, hi) is 
  if lo >= hi || lo < 0 then 
    return
  
  // 分区
  p := partition(A, lo, hi) 
  
  // 递归
  quicksort(A, lo, p - 1) 
  quicksort(A, p + 1, hi)

  • 子问题个数 $a=2$

  • 子问题数据规模缩小倍数

    • 如果分区分的好，$b=2$

    • 如果分区没分好，例如分区1 的数据是 0，分区 2 的数据是 $n-1$

  • 除递归外，主要时间花在分区上，它可以用 $f(n) = n$ 表示

情况1 - 分区分的好

$T(n) = 2T(\frac{n}{2}) + n$

  • 此时 $x=1=c$，时间复杂度 $\Theta(n\log{n})$

情况2 - 分区没分好

$T(n) = T(n-1) + T(1) + n$

  • 此时不能用主定理求解

递归时间复杂度-展开求解

像下面的递归式，都不能用主定理求解

例1 - 递归求和

long sum(long n) {
    if (n == 1) {
        return 1;
    }
    return n + sum(n - 1);
}

$T(n) = T(n-1) + c$，$T(1) = c$

下面为展开过程

$T(n) = T(n-2) + c + c$

$T(n) = T(n-3) + c + c + c$

...

$T(n) = T(n-(n-1)) + (n-1)c$

  • 其中 $T(n-(n-1))$ 即 $T(1)$

  • 带入求得 $T(n) = c + (n-1)c = nc$

时间复杂度为 $O(n)$

例2 - 递归冒泡排序

void bubble(int[] a, int high) {
    if(0 == high) {
        return;
    }
    for (int i = 0; i < high; i++) {
        if (a[i] > a[i + 1]) {
            swap(a, i, i + 1);
        }
    }
    bubble(a, high - 1);
}

$T(n) = T(n-1) + n$，$T(1) = c$

下面为展开过程

$T(n) = T(n-2) + (n-1) + n$

$T(n) = T(n-3) + (n-2) + (n-1) + n$

...

$T(n) = T(1) + 2 + ... + n = T(1) + (n-1)\frac{2+n}{2} = c + \frac{n^2}{2} + \frac{n}{2} -1$

时间复杂度 $O(n^2)$

注：

  • 等差数列求和为 $个数*\frac{\vert首项-末项\vert}{2}$

例3 - 递归快排

快速排序分区没分好的极端情况

$T(n) = T(n-1) + T(1) + n$，$T(1) = c$

$T(n) = T(n-1) + c + n$

下面为展开过程

$T(n) = T(n-2) + c + (n-1) + c + n$

$T(n) = T(n-3) + c + (n-2) + c + (n-1) + c + n$

...

$T(n) = T(n-(n-1)) + (n-1)c + 2+...+n = \frac{n^2}{2} + \frac{2cn+n}{2} -1$

时间复杂度 $O(n^2)$

不会推导的同学可以进入 Wolfram|Alpha: Computational Intelligence

  • 例1 输入 f(n) = f(n - 1) + c, f(1) = c

  • 例2 输入 f(n) = f(n - 1) + n, f(1) = c

  • 例3 输入 f(n) = f(n - 1) + n + c, f(1) = c

4. 队列

概述

计算机科学中，queue 是以顺序的方式维护的一组数据集合，在一端添加数据，从另一端移除数据。习惯来说，添加的一端称为尾，移除的一端称为头，就如同生活中的排队买商品

先定义一个简化的队列接口

public interface Queue {

    /**
     * 向队列尾插入值
     * @param value 待插入值
     * @return 插入成功返回 true, 插入失败返回 false
     */
    boolean offer(E value);

    /**
     * 从对列头获取值, 并移除
     * @return 如果队列非空返回对头值, 否则返回 null
     */
    E poll();

    /**
     * 从对列头获取值, 不移除
     * @return 如果队列非空返回对头值, 否则返回 null
     */
    E peek();

    /**
     * 检查队列是否为空
     * @return 空返回 true, 否则返回 false
     */
    boolean isEmpty();

    /**
     * 检查队列是否已满
     * @return 满返回 true, 否则返回 false
     */
    boolean isFull();
}

链表实现

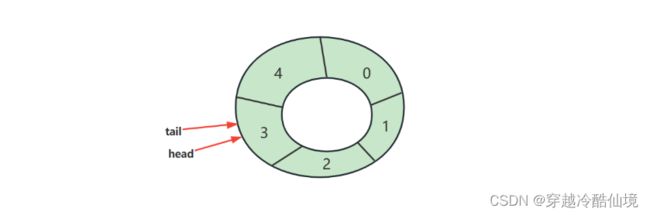
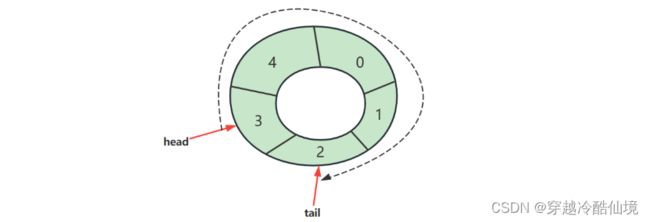
下面以单向环形带哨兵链表方式来实现队列

基础数据结构_第12张图片

 基础数据结构_第13张图片

基础数据结构_第14张图片 

 代码

public class LinkedListQueue
        implements Queue, Iterable {

    private static class Node {
        E value;
        Node next;

        public Node(E value, Node next) {
            this.value = value;
            this.next = next;
        }
    }

    private Node head = new Node<>(null, null);
    private Node tail = head;
    private int size = 0;
    private int capacity = Integer.MAX_VALUE;

    {
        tail.next = head;
    }

    public LinkedListQueue() {
    }

    public LinkedListQueue(int capacity) {
        this.capacity = capacity;
    }

    @Override
    public boolean offer(E value) {
        if (isFull()) {
            return false;
        }
        Node added = new Node<>(value, head);
        tail.next = added;
        tail = added;
        size++;
        return true;
    }

    @Override
    public E poll() {
        if (isEmpty()) {
            return null;
        }
        Node first = head.next;
        head.next = first.next;
        if (first == tail) {
            tail = head;
        }
        size--;
        return first.value;
    }

    @Override
    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return head.next.value;
    }

    @Override
    public boolean isEmpty() {
        return head == tail;
    }

    @Override
    public boolean isFull() {
        return size == capacity;
    }

    @Override
    public Iterator iterator() {
        return new Iterator() {
            Node p = head.next;
            @Override
            public boolean hasNext() {
                return p != head;
            }
            @Override
            public E next() {
                E value = p.value;
                p = p.next;
                return value;
            }
        };
    }
}

环形数组实现

好处

  1. 对比普通数组，起点和终点更为自由，不用考虑数据移动

  2. “环”意味着不会存在【越界】问题

  3. 数组性能更佳

  4. 环形数组比较适合实现有界队列、RingBuffer 等

基础数据结构_第15张图片

 

下标计算

例如，数组长度是 5，当前位置是 3 ，向前走 2 步，此时下标为 $(3 + 2)\%5 = 0$

基础数据结构_第16张图片

 

注意：

  • 如果 step = 1，也就是一次走一步，可以在 >= length 时重置为 0 即可

  • cur 当前指针位置

  • step 前进步数

  • length 数组长度

 判断空

基础数据结构_第17张图片

 

判断满

基础数据结构_第18张图片

 

满之后的策略可以根据业务需求决定

  • 例如我们要实现的环形队列，满之后就拒绝入队

代码

public class ArrayQueue implements Queue, Iterable{

    private int head = 0;
    private int tail = 0;
    private final E[] array;
    private final int length;

    @SuppressWarnings("all")
    public ArrayQueue(int capacity) {
        length = capacity + 1;
        array = (E[]) new Object[length];
    }

    @Override
    public boolean offer(E value) {
        if (isFull()) {
            return false;
        }
        array[tail] = value;
        tail = (tail + 1) % length;
        return true;
    }

    @Override
    public E poll() {
        if (isEmpty()) {
            return null;
        }
        E value = array[head];
        head = (head + 1) % length;
        return value;
    }

    @Override
    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return array[head];
    }

    @Override
    public boolean isEmpty() {
        return tail == head;
    }

    @Override
    public boolean isFull() {
        return (tail + 1) % length == head;
    }

    @Override
    public Iterator iterator() {
        return new Iterator() {
            int p = head;
            @Override
            public boolean hasNext() {
                return p != tail;
            }

            @Override
            public E next() {
                E value = array[p];
                p = (p + 1) % array.length;
                return value;
            }
        };
    }
}

判断空、满方法2

引入 size

public class ArrayQueue2 implements Queue, Iterable {

    private int head = 0;
    private int tail = 0;
    private final E[] array;
    private final int capacity;
    private int size = 0;

    @SuppressWarnings("all")
    public ArrayQueue2(int capacity) {
        this.capacity = capacity;
        array = (E[]) new Object[capacity];
    }

    @Override
    public boolean offer(E value) {
        if (isFull()) {
            return false;
        }
        array[tail] = value;
        tail = (tail + 1) % capacity;
        size++;
        return true;
    }

    @Override
    public E poll() {
        if (isEmpty()) {
            return null;
        }
        E value = array[head];
        head = (head + 1) % capacity;
        size--;
        return value;
    }

    @Override
    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return array[head];
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    @Override
    public boolean isFull() {
        return size == capacity;
    }

    @Override
    public Iterator iterator() {
        return new Iterator() {
            int p = head;

            @Override
            public boolean hasNext() {
                return p != tail;
            }

            @Override
            public E next() {
                E value = array[p];
                p = (p + 1) % capacity;
                return value;
            }
        };
    }
}

判断空、满方法3

  • head 和 tail 不断递增，用到索引时，再用它们进行计算，两个问题

    • 如何保证 head 和 tail 自增超过正整数最大值的正确性

    • 如何让取模运算性能更高

  • 答案：让 capacity 为 2 的幂

public class ArrayQueue3 implements Queue, Iterable {

    private int head = 0;
    private int tail = 0;
    private final E[] array;
    private final int capacity;

    @SuppressWarnings("all")
    public ArrayQueue3(int capacity) {
        if ((capacity & capacity - 1) != 0) {
            throw new IllegalArgumentException("capacity 必须为 2 的幂");
        }
        this.capacity = capacity;
        array = (E[]) new Object[this.capacity];
    }

    @Override
    public boolean offer(E value) {
        if (isFull()) {
            return false;
        }
        array[tail & capacity - 1] = value;
        tail++;
        return true;
    }

    @Override
    public E poll() {
        if (isEmpty()) {
            return null;
        }
        E value = array[head & capacity - 1];
        head++;
        return value;
    }

    @Override
    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return array[head & capacity - 1];
    }

    @Override
    public boolean isEmpty() {
        return tail - head == 0;
    }

    @Override
    public boolean isFull() {
        return tail - head == capacity;
    }

    @Override
    public Iterator iterator() {
        return new Iterator() {
            int p = head;

            @Override
            public boolean hasNext() {
                return p != tail;
            }

            @Override
            public E next() {
                E value = array[p & capacity - 1];
                p++;
                return value;
            }
        };
    }
}

5. 栈

概述

计算机科学中，stack 是一种线性的数据结构，只能在其一端添加数据和移除数据。习惯来说，这一端称之为栈顶，另一端不能操作数据的称之为栈底，就如同生活中的一摞书

先提供一个栈接口

public interface Stack {
    /**
     * 向栈顶压入元素
     * @param value 待压入值
     * @return 压入成功返回 true, 否则返回 false
     */
    boolean push(E value);

    /**
     * 从栈顶弹出元素
     * @return 栈非空返回栈顶元素, 栈为空返回 null
     */
    E pop();

    /**
     * 返回栈顶元素, 不弹出
     * @return 栈非空返回栈顶元素, 栈为空返回 null
     */
    E peek();

    /**
     * 判断栈是否为空
     * @return 空返回 true, 否则返回 false
     */
    boolean isEmpty();

    /**
     * 判断栈是否已满
     * @return 满返回 true, 否则返回 false
     */
    boolean isFull();
}

链表实现

public class LinkedListStack implements Stack, Iterable {

    private final int capacity;
    private int size;
    private final Node head = new Node<>(null, null);

    public LinkedListStack(int capacity) {
        this.capacity = capacity;
    }

    @Override
    public boolean push(E value) {
        if (isFull()) {
            return false;
        }
        head.next = new Node<>(value, head.next);
        size++;
        return true;
    }

    @Override
    public E pop() {
        if (isEmpty()) {
            return null;
        }
        Node first = head.next;
        head.next = first.next;
        size--;
        return first.value;
    }

    @Override
    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return head.next.value;
    }

    @Override
    public boolean isEmpty() {
        return head.next == null;
    }

    @Override
    public boolean isFull() {
        return size == capacity;
    }

    @Override
    public Iterator iterator() {
        return new Iterator() {
            Node p = head.next;
            @Override
            public boolean hasNext() {
                return p != null;
            }

            @Override
            public E next() {
                E value = p.value;
                p = p.next;
                return value;
            }
        };
    }

    static class Node {
        E value;
        Node next;

        public Node(E value, Node next) {
            this.value = value;
            this.next = next;
        }
    }
}

        

数组实现

public class ArrayStack implements Stack, Iterable{
    private final E[] array;
    private int top = 0;

    @SuppressWarnings("all")
    public ArrayStack(int capacity) {
        this.array = (E[]) new Object[capacity];
    }

    @Override
    public boolean push(E value) {
        if (isFull()) {
            return false;
        }
        array[top++] = value;
        return true;
    }

    @Override
    public E pop() {
        if (isEmpty()) {
            return null;
        }
        return array[--top];
    }

    @Override
    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return array[top-1];
    }

    @Override
    public boolean isEmpty() {
        return top == 0;
    }

    @Override
    public boolean isFull() {
        return top == array.length;
    }

    @Override
    public Iterator iterator() {
        return new Iterator() {
            int p = top;
            @Override
            public boolean hasNext() {
                return p > 0;
            }

            @Override
            public E next() {
                return array[--p];
            }
        };
    }
}

应用

模拟如下方法调用

public static void main(String[] args) {
    System.out.println("main1");
    System.out.println("main2");
    method1();
    method2();
    System.out.println("main3");
}

public static void method1() {
    System.out.println("method1");
    method3();
}

public static void method2() {
    System.out.println("method2");
}

public static void method3() {
    System.out.println("method3");
}

模拟代码

public class CPU {
    static class Frame {
        int exit;

        public Frame(int exit) {
            this.exit = exit;
        }
    }
    static int pc = 1; // 模拟程序计数器 Program counter
    static ArrayStack stack = new ArrayStack<>(100); // 模拟方法调用栈

    public static void main(String[] args) {
        stack.push(new Frame(-1));
        while (!stack.isEmpty()) {
            switch (pc) {
                case 1 -> {
                    System.out.println("main1");
                    pc++;
                }
                case 2 -> {
                    System.out.println("main2");
                    pc++;
                }
                case 3 -> {
                    stack.push(new Frame(pc + 1));
                    pc = 100;
                }
                case 4 -> {
                    stack.push(new Frame(pc + 1));
                    pc = 200;
                }
                case 5 -> {
                    System.out.println("main3");
                    pc = stack.pop().exit;
                }
                case 100 -> {
                    System.out.println("method1");
                    stack.push(new Frame(pc + 1));
                    pc = 300;
                }
                case 101 -> {
                    pc = stack.pop().exit;
                }
                case 200 -> {
                    System.out.println("method2");
                    pc = stack.pop().exit;
                }
                case 300 -> {
                    System.out.println("method3");
                    pc = stack.pop().exit;
                }
            }
        }
    }
}

6. 双端队列

概述

双端队列、队列、栈对比

定义 特点
队列 一端删除（头）另一端添加（尾） First In First Out
栈 一端删除和添加（顶） Last In First Out
双端队列 两端都可以删除、添加
优先级队列 优先级高者先出队
延时队列 根据延时时间确定优先级
并发非阻塞队列 队列空或满时不阻塞
并发阻塞队列 队列空时删除阻塞、队列满时添加阻塞

接口定义

public interface Deque {

    boolean offerFirst(E e);

    boolean offerLast(E e);

    E pollFirst();

    E pollLast();

    E peekFirst();

    E peekLast();
    
    boolean isEmpty();

    boolean isFull();
}

 

链表实现

/**
 * 基于环形链表的双端队列
 * @param  元素类型
 */
public class LinkedListDeque implements Deque, Iterable {

    @Override
    public boolean offerFirst(E e) {
        if (isFull()) {
            return false;
        }
        size++;
        Node a = sentinel;
        Node b = sentinel.next;
        Node offered = new Node<>(a, e, b);
        a.next = offered;
        b.prev = offered;
        return true;
    }

    @Override
    public boolean offerLast(E e) {
        if (isFull()) {
            return false;
        }
        size++;
        Node a = sentinel.prev;
        Node b = sentinel;
        Node offered = new Node<>(a, e, b);
        a.next = offered;
        b.prev = offered;
        return true;
    }

    @Override
    public E pollFirst() {
        if (isEmpty()) {
            return null;
        }
        Node a = sentinel;
        Node polled = sentinel.next;
        Node b = polled.next;
        a.next = b;
        b.prev = a;
        size--;
        return polled.value;
    }

    @Override
    public E pollLast() {
        if (isEmpty()) {
            return null;
        }
        Node polled = sentinel.prev;
        Node a = polled.prev;
        Node b = sentinel;
        a.next = b;
        b.prev = a;
        size--;
        return polled.value;
    }

    @Override
    public E peekFirst() {
        if (isEmpty()) {
            return null;
        }
        return sentinel.next.value;
    }

    @Override
    public E peekLast() {
        if (isEmpty()) {
            return null;
        }
        return sentinel.prev.value;
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    @Override
    public boolean isFull() {
        return size == capacity;
    }

    @Override
    public Iterator iterator() {
        return new Iterator() {
            Node p = sentinel.next;
            @Override
            public boolean hasNext() {
                return p != sentinel;
            }

            @Override
            public E next() {
                E value = p.value;
                p = p.next;
                return value;
            }
        };
    }

    static class Node {
        Node prev;
        E value;
        Node next;

        public Node(Node prev, E value, Node next) {
            this.prev = prev;
            this.value = value;
            this.next = next;
        }
    }

    Node sentinel = new Node<>(null, null, null);
    int capacity;
    int size;

    public LinkedListDeque(int capacity) {
        sentinel.next = sentinel;
        sentinel.prev = sentinel;
        this.capacity = capacity;
    }
}

数组实现

/**
 * 基于循环数组实现, 特点
 * 
    
 *     
  • tail 停下来的位置不存储, 会浪费一个位置
    • 
 * 

 * @param 
 */
public class ArrayDeque1 implements Deque, Iterable {

    /*
                    h
            t
        0   1   2   3
        b           a
     */
    @Override
    public boolean offerFirst(E e) {
        if (isFull()) {
            return false;
        }
        head = dec(head, array.length);
        array[head] = e;
        return true;
    }

    @Override
    public boolean offerLast(E e) {
        if (isFull()) {
            return false;
        }
        array[tail] = e;
        tail = inc(tail, array.length);
        return true;
    }

    @Override
    public E pollFirst() {
        if (isEmpty()) {
            return null;
        }
        E e = array[head];
        array[head] = null;
        head = inc(head, array.length);
        return e;
    }

    @Override
    public E pollLast() {
        if (isEmpty()) {
            return null;
        }
        tail = dec(tail, array.length);
        E e = array[tail];
        array[tail] = null;
        return e;
    }

    @Override
    public E peekFirst() {
        if (isEmpty()) {
            return null;
        }
        return array[head];
    }

    @Override
    public E peekLast() {
        if (isEmpty()) {
            return null;
        }
        return array[dec(tail, array.length)];
    }

    @Override
    public boolean isEmpty() {
        return head == tail;
    }

    @Override
    public boolean isFull() {
        if (tail > head) {
            return tail - head == array.length - 1;
        } else if (tail < head) {
            return head - tail == 1;
        } else {
            return false;
        }
    }

    @Override
    public Iterator iterator() {
        return new Iterator() {
            int p = head;
            @Override
            public boolean hasNext() {
                return p != tail;
            }

            @Override
            public E next() {
                E e = array[p];
                p = inc(p, array.length);
                return e;
            }
        };
    }

    E[] array;
    int head;
    int tail;

    @SuppressWarnings("unchecked")
    public ArrayDeque1(int capacity) {
        array = (E[]) new Object[capacity + 1];
    }

    static int inc(int i, int length) {
        if (i + 1 >= length) {
            return 0;
        }
        return i + 1;
    }

    static int dec(int i, int length) {
        if (i - 1 < 0) {
            return length - 1;
        }
        return i - 1;
    }
}

数组实现中，如果存储的是基本类型，那么无需考虑内存释放，例如

基础数据结构_第19张图片

 但如果存储的是引用类型，应当设置该位置的引用为 null，以便内存及时释放

基础数据结构_第20张图片

 

7. 优先级队列

无序数组实现

要点

  1. 入队保持顺序

  2. 出队前找到优先级最高的出队，相当于一次选择排序

public class PriorityQueue1 implements Queue {

    Priority[] array;
    int size;

    public PriorityQueue1(int capacity) {
        array = new Priority[capacity];
    }

    @Override // O(1)
    public boolean offer(E e) {
        if (isFull()) {
            return false;
        }
        array[size++] = e;
        return true;
    }

    // 返回优先级最高的索引值
    private int selectMax() {
        int max = 0;
        for (int i = 1; i < size; i++) {
            if (array[i].priority() > array[max].priority()) {
                max = i;
            }
        }
        return max;
    }

    @Override // O(n)
    public E poll() {
        if (isEmpty()) {
            return null;
        }
        int max = selectMax();
        E e = (E) array[max];
        remove(max);
        return e;
    }

    private void remove(int index) {
        if (index < size - 1) {
            System.arraycopy(array, index + 1,
                    array, index, size - 1 - index);
        }
        array[--size] = null; // help GC
    }

    @Override
    public E peek() {
        if (isEmpty()) {
            return null;
        }
        int max = selectMax();
        return (E) array[max];
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    @Override
    public boolean isFull() {
        return size == array.length;
    }
}

有序数组实现

要点

  1. 入队后排好序，优先级最高的排列在尾部

  2. 出队只需删除尾部元素即可

public class PriorityQueue2 implements Queue {

    Priority[] array;
    int size;

    public PriorityQueue2(int capacity) {
        array = new Priority[capacity];
    }

    // O(n)
    @Override
    public boolean offer(E e) {
        if (isFull()) {
            return false;
        }
        insert(e);
        size++;
        return true;
    }

    // 一轮插入排序
    private void insert(E e) {
        int i = size - 1;
        while (i >= 0 && array[i].priority() > e.priority()) {
            array[i + 1] = array[i];
            i--;
        }
        array[i + 1] = e;
    }

    // O(1)
    @Override
    public E poll() {
        if (isEmpty()) {
            return null;
        }
        E e = (E) array[size - 1];
        array[--size] = null; // help GC
        return e;
    }

    @Override
    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return (E) array[size - 1];
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    @Override
    public boolean isFull() {
        return size == array.length;
    }
}

堆实现

计算机科学中，堆是一种基于树的数据结构，通常用完全二叉树实现。堆的特性如下

  • 在大顶堆中，任意节点 C 与它的父节点 P 符合 $P.value \geq C.value$

  • 而小顶堆中，任意节点 C 与它的父节点 P 符合 $P.value \leq C.value$

  • 最顶层的节点（没有父亲）称之为 root 根节点

例1 - 满二叉树（Full Binary Tree）特点：每一层都是填满的

基础数据结构_第21张图片

例2 - 完全二叉树（Complete Binary Tree）特点：最后一层可能未填满，靠左对齐

基础数据结构_第22张图片 

例3 - 大顶堆

基础数据结构_第23张图片 

 

例4 - 小顶堆

基础数据结构_第24张图片

 

完全二叉树可以使用数组来表示

基础数据结构_第25张图片

 

特征

  • 如果从索引 0 开始存储节点数据

    • 节点 $i$ 的父节点为 $floor((i-1)/2)$，当 $i>0$ 时

    • 节点 $i$ 的左子节点为 $2i+1$，右子节点为 $2i+2$，当然它们得 $< size$

  • 如果从索引 1 开始存储节点数据

    • 节点 $i$ 的父节点为 $floor(i/2)$，当 $i > 1$ 时

    • 节点 $i$ 的左子节点为 $2i$，右子节点为 $2i+1$，同样得 $< size$

代码

public class PriorityQueue4 implements Queue {

    Priority[] array;
    int size;

    public PriorityQueue4(int capacity) {
        array = new Priority[capacity];
    }

    @Override
    public boolean offer(E offered) {
        if (isFull()) {
            return false;
        }
        int child = size++;
        int parent = (child - 1) / 2;
        while (child > 0 && offered.priority() > array[parent].priority()) {
            array[child] = array[parent];
            child = parent;
            parent = (child - 1) / 2;
        }
        array[child] = offered;
        return true;
    }


    private void swap(int i, int j) {
        Priority t = array[i];
        array[i] = array[j];
        array[j] = t;
    }

    @Override
    public E poll() {
        if (isEmpty()) {
            return null;
        }
        swap(0, size - 1);
        size--;
        Priority e = array[size];
        array[size] = null;
        
        shiftDown(0);        
        return (E) e;
    }

    void shiftDown(int parent) {
        int left = 2 * parent + 1;
        int right = left + 1;
        int max = parent;
        if (left < size && array[left].priority() > array[max].priority()) {
            max = left;
        }
        if (right < size && array[right].priority() > array[max].priority()) {
            max = right;
        }
        if (max != parent) {
            swap(max, parent);
            shiftDown(max);
        }
    }

    @Override
    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return (E) array[0];
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    @Override
    public boolean isFull() {
        return size == array.length;
    }
}

8. 阻塞队列

之前的队列在很多场景下都不能很好地工作，例如

  1. 大部分场景要求分离向队列放入（生产者）、从队列拿出（消费者）两个角色、它们得由不同的线程来担当，而之前的实现根本没有考虑线程安全问题

  2. 队列为空，那么在之前的实现里会返回 null，如果就是硬要拿到一个元素呢？只能不断循环尝试

  3. 队列为满，那么再之前的实现里会返回 false，如果就是硬要塞入一个元素呢？只能不断循环尝试

因此我们需要解决的问题有

  1. 用锁保证线程安全

  2. 用条件变量让等待非空线程与等待不满线程进入等待状态，而不是不断循环尝试，让 CPU 空转

有基友对线程安全还没有足够的认识，下面举一个反例，两个线程都要执行入队操作（几乎在同一时刻）

public class TestThreadUnsafe {
    private final String[] array = new String[10];
    private int tail = 0;

    public void offer(String e) {
        array[tail] = e;
        tail++;
    }

    @Override
    public String toString() {
        return Arrays.toString(array);
    }

    public static void main(String[] args) {
        TestThreadUnsafe queue = new TestThreadUnsafe();
        new Thread(()-> queue.offer("e1"), "t1").start();
        new Thread(()-> queue.offer("e2"), "t2").start();
    }
}

执行的时间序列如下，假设初始状态 tail = 0，在执行过程中由于 CPU 在两个线程之间切换，造成了指令交错

线程1 线程2 说明
array[tail]=e1 线程1 向 tail 位置加入 e1 这个元素，但还没来得及执行 tail++
array[tail]=e2 线程2 向 tail 位置加入 e2 这个元素，覆盖掉了 e1
tail++ tail 自增为1
tail++ tail 自增为2
最后状态 tail 为 2，数组为 [e2, null, null ...]

糟糕的是，由于指令交错的顺序不同，得到的结果不止以上一种，宏观上造成混乱的效果

单锁实现

Java 中要防止代码段交错执行，需要使用锁，有两种选择

  • synchronized 代码块，属于关键字级别提供锁保护，功能少

  • ReentrantLock 类，功能丰富

以 ReentrantLock 为例

ReentrantLock lock = new ReentrantLock();

public void offer(String e) {
    lock.lockInterruptibly();
    try {
        array[tail] = e;
        tail++;
    } finally {
        lock.unlock();
    }
}

 

只要两个线程执行上段代码时，锁对象是同一个，就能保证 try 块内的代码的执行不会出现指令交错现象，即执行顺序只可能是下面两种情况之一

线程1 线程2 说明
lock.lockInterruptibly() t1对锁对象上锁
array[tail]=e1
lock.lockInterruptibly() 即使 CPU 切换到线程2，但由于t1已经对该对象上锁，因此线程2卡在这儿进不去
tail++ 切换回线程1 执行后续代码
lock.unlock() 线程1 解锁
array[tail]=e2 线程2 此时才能获得锁，执行它的代码
tail++

  • 另一种情况是线程2 先获得锁，线程1 被挡在外面

  • 要明白保护的本质，本例中是保护的是 tail 位置读写的安全

事情还没有完，上面的例子是队列还没有放满的情况，考虑下面的代码（这回锁同时保护了 tail 和 size 的读写安全）

ReentrantLock lock = new ReentrantLock();
int size = 0;

public void offer(String e) {
    lock.lockInterruptibly();
    try {
        if(isFull()) {
            // 满了怎么办?
        }
        array[tail] = e;
        tail++;
        
        size++;
    } finally {
        lock.unlock();
    }
}

private boolean isFull() {
    return size == array.length;
}

之前是返回 false 表示添加失败，前面分析过想达到这么一种效果：

  • 在队列满时，不是立刻返回，而是当前线程进入等待

  • 什么时候队列不满了，再唤醒这个等待的线程，从上次的代码处继续向下运行

ReentrantLock 可以配合条件变量来实现，代码进化为

ReentrantLock lock = new ReentrantLock();
Condition tailWaits = lock.newCondition(); // 条件变量
int size = 0;

public void offer(String e) {
    lock.lockInterruptibly();
    try {
        while (isFull()) {
            tailWaits.await();	// 当队列满时, 当前线程进入 tailWaits 等待
        }
        array[tail] = e;
        tail++;
        
        size++;
    } finally {
        lock.unlock();
    }
}

private boolean isFull() {
    return size == array.length;
}

  • 条件变量底层也是个队列，用来存储这些需要等待的线程，当队列满了，就会将 offer 线程加入条件队列，并暂时释放锁

  • 将来我们的队列如果不满了（由 poll 线程那边得知）可以调用 tailWaits.signal() 来唤醒 tailWaits 中首个等待的线程，被唤醒的线程会再次抢到锁，从上次 await 处继续向下运行

思考为何要用 while 而不是 if，设队列容量是 3

操作前 offer(4) offer(5) poll() 操作后
[1 2 3] 队列满，进入tailWaits 等待 [1 2 3]
[1 2 3] 取走 1，队列不满，唤醒线程 [2 3]
[2 3] 抢先获得锁，发现不满，放入 5 [2 3 5]
[2 3 5] 从上次等待处直接向下执行
[2 3 5 ?]

关键点：

  • 从 tailWaits 中唤醒的线程，会与新来的 offer 的线程争抢锁，谁能抢到是不一定的，如果后者先抢到，就会导致条件又发生变化

  • 这种情况称之为虚假唤醒，唤醒后应该重新检查条件，看是不是得重新进入等待

最后的实现代码

/**
 * 单锁实现
 * @param  元素类型
 */
public class BlockingQueue1 implements BlockingQueue {
    private final E[] array;
    private int head = 0;
    private int tail = 0;
    private int size = 0; // 元素个数

    @SuppressWarnings("all")
    public BlockingQueue1(int capacity) {
        array = (E[]) new Object[capacity];
    }

    ReentrantLock lock = new ReentrantLock();
    Condition tailWaits = lock.newCondition();
    Condition headWaits = lock.newCondition();

    @Override
    public void offer(E e) throws InterruptedException {
        lock.lockInterruptibly();
        try {
            while (isFull()) {
                tailWaits.await();
            }
            array[tail] = e;
            if (++tail == array.length) {
                tail = 0;
            }
            size++;
            headWaits.signal();
        } finally {
            lock.unlock();
        }
    }

    @Override
    public void offer(E e, long timeout) throws InterruptedException {
        lock.lockInterruptibly();
        try {
            long t = TimeUnit.MILLISECONDS.toNanos(timeout);
            while (isFull()) {
                if (t <= 0) {
                    return;
                }
                t = tailWaits.awaitNanos(t);
            }
            array[tail] = e;
            if (++tail == array.length) {
                tail = 0;
            }
            size++;
            headWaits.signal();
        } finally {
            lock.unlock();
        }
    }

    @Override
    public E poll() throws InterruptedException {
        lock.lockInterruptibly();
        try {
            while (isEmpty()) {
                headWaits.await();
            }
            E e = array[head];
            array[head] = null; // help GC
            if (++head == array.length) {
                head = 0;
            }
            size--;
            tailWaits.signal();
            return e;
        } finally {
            lock.unlock();
        }
    }

    private boolean isEmpty() {
        return size == 0;
    }

    private boolean isFull() {
        return size == array.length;
    }
}

  • public void offer(E e, long timeout) throws InterruptedException 是带超时的版本，可以只等待一段时间，而不是永久等下去，类似的 poll 也可以做带超时的版本，这个留给大家了

注意

  • JDK 中 BlockingQueue 接口的方法命名与我的示例有些差异

    • 方法 offer(E e) 是非阻塞的实现，阻塞实现方法为 put(E e)

    • 方法 poll() 是非阻塞的实现，阻塞实现方法为 take()

双锁实现

单锁的缺点在于：

  • 生产和消费几乎是不冲突的，唯一冲突的是生产者和消费者它们有可能同时修改 size

  • 冲突的主要是生产者之间：多个 offer 线程修改 tail

  • 冲突的还有消费者之间：多个 poll 线程修改 head

如果希望进一步提高性能，可以用两把锁

  • 一把锁保护 tail

  • 另一把锁保护 head

ReentrantLock headLock = new ReentrantLock();  // 保护 head 的锁
Condition headWaits = headLock.newCondition(); // 队列空时，需要等待的线程集合

ReentrantLock tailLock = new ReentrantLock();  // 保护 tail 的锁
Condition tailWaits = tailLock.newCondition(); // 队列满时，需要等待的线程集合

先看看 offer 方法的初步实现

上面代码的缺点是 size 并不受 tailLock 保护，tailLock 与 headLock 是两把不同的锁，并不能实现互斥的效果。因此，size 需要用下面的代码保证原子性

AtomicInteger size = new AtomicInteger(0);	   // 保护 size 的原子变量

size.getAndIncrement(); // 自增
size.getAndDecrement(); // 自减

代码修改为

@Override
public void offer(E e) throws InterruptedException {
    tailLock.lockInterruptibly();
    try {
        // 队列满等待
        while (isFull()) {
            tailWaits.await();
        }
        
        // 不满则入队
        array[tail] = e;
        if (++tail == array.length) {
            tail = 0;
        }
        
        // 修改 size
        size.getAndIncrement();
        
    } finally {
        tailLock.unlock();
    }
}

对称地，可以写出 poll 方法

@Override
public E poll() throws InterruptedException {
    E e;
    headLock.lockInterruptibly();
    try {
        // 队列空等待
        while (isEmpty()) {
            headWaits.await();
        }
        
        // 不空则出队
        e = array[head];
        if (++head == array.length) {
            head = 0;
        }
        
        // 修改 size
        size.getAndDecrement();
        
    } finally {
        headLock.unlock();
    }
    return e;
}

下面来看一个难题，就是如何通知 headWaits 和 tailWaits 中等待的线程，比如 poll 方法拿走一个元素，通知 tailWaits：我拿走一个，不满了噢，你们可以放了，因此代码改为

@Override
public E poll() throws InterruptedException {
    E e;
    headLock.lockInterruptibly();
    try {
        // 队列空等待
        while (isEmpty()) {
            headWaits.await();
        }
        
        // 不空则出队
        e = array[head];
        if (++head == array.length) {
            head = 0;
        }
        
        // 修改 size
        size.getAndDecrement();
        
        // 通知 tailWaits 不满（有问题）
        tailWaits.signal();
        
    } finally {
        headLock.unlock();
    }
    return e;
}

问题在于要使用这些条件变量的 await()， signal() 等方法需要先获得与之关联的锁，上面的代码若直接运行会出现以下错误

java.lang.IllegalMonitorStateException

那有基友说，加上锁不就行了吗，于是写出了下面的代码

基础数据结构_第26张图片

基础数据结构_第27张图片 

两把锁这么嵌套使用，非常容易出现死锁，如下所示

基础数据结构_第28张图片 

基础数据结构_第29张图片 

 因此得避免嵌套，两段加锁的代码变成了下面平级的样子 基础数据结构_第30张图片

基础数据结构_第31张图片 

性能还可以进一步提升

  1. 代码调整后 offer 并没有同时获取 tailLock 和 headLock 两把锁，因此两次加锁之间会有空隙，这个空隙内可能有其它的 offer 线程添加了更多的元素，那么这些线程都要执行 signal()，通知 poll 线程队列非空吗？

    • 每次调用 signal() 都需要这些 offer 线程先获得 headLock 锁，成本较高，要想法减少 offer 线程获得 headLock 锁的次数

    • 可以加一个条件：当 offer 增加前队列为空，即从 0 变化到不空，才由此 offer 线程来通知 headWaits，其它情况不归它管

  2. 队列从 0 变化到不空，会唤醒一个等待的 poll 线程，这个线程被唤醒后，肯定能拿到 headLock 锁，因此它具备了唤醒 headWaits 上其它 poll 线程的先决条件。如果检查出此时有其它 offer 线程新增了元素（不空，但不是从0变化而来），那么不妨由此 poll 线程来唤醒其它 poll 线程

这个技巧被称之为级联通知（cascading notifies），类似的原因

  1. 在 poll 时队列从满变化到不满，才由此 poll 线程来唤醒一个等待的 offer 线程，目的也是为了减少 poll 线程对 tailLock 上锁次数，剩下等待的 offer 线程由这个 offer 线程间接唤醒

最终的代码为

public class BlockingQueue2 implements BlockingQueue {

    private final E[] array;
    private int head = 0;
    private int tail = 0;
    private final AtomicInteger size = new AtomicInteger(0);
    ReentrantLock headLock = new ReentrantLock();
    Condition headWaits = headLock.newCondition();
    ReentrantLock tailLock = new ReentrantLock();
    Condition tailWaits = tailLock.newCondition();

    public BlockingQueue2(int capacity) {
        this.array = (E[]) new Object[capacity];
    }

    @Override
    public void offer(E e) throws InterruptedException {
        int c;
        tailLock.lockInterruptibly();
        try {
            while (isFull()) {
                tailWaits.await();
            }
            array[tail] = e;
            if (++tail == array.length) {
                tail = 0;
            }            
            c = size.getAndIncrement();
            // a. 队列不满, 但不是从满->不满, 由此offer线程唤醒其它offer线程
            if (c + 1 < array.length) {
                tailWaits.signal();
            }
        } finally {
            tailLock.unlock();
        }
        // b. 从0->不空, 由此offer线程唤醒等待的poll线程
        if (c == 0) {
            headLock.lock();
            try {
                headWaits.signal();
            } finally {
                headLock.unlock();
            }
        }
    }

    @Override
    public E poll() throws InterruptedException {
        E e;
        int c;
        headLock.lockInterruptibly();
        try {
            while (isEmpty()) {
                headWaits.await(); 
            }
            e = array[head]; 
            if (++head == array.length) {
                head = 0;
            }
            c = size.getAndDecrement();
            // b. 队列不空, 但不是从0变化到不空，由此poll线程通知其它poll线程
            if (c > 1) {
                headWaits.signal();
            }
        } finally {
            headLock.unlock();
        }
        // a. 从满->不满, 由此poll线程唤醒等待的offer线程
        if (c == array.length) {
            tailLock.lock();
            try {
                tailWaits.signal();
            } finally {
                tailLock.unlock();
            }
        }
        return e;
    }

    private boolean isEmpty() {
        return size.get() == 0;
    }

    private boolean isFull() {
        return size.get() == array.length;
    }

}

 双锁实现的非常精巧，据说作者 Doug Lea 花了一年的时间才完善了此段代码

9. 堆

以大顶堆为例，相对于之前的优先级队列，增加了堆化等方法

public class MaxHeap {
    int[] array;
    int size;

    public MaxHeap(int capacity) {
        this.array = new int[capacity];
    }

    /**
     * 获取堆顶元素
     *
     * @return 堆顶元素
     */
    public int peek() {
        return array[0];
    }

    /**
     * 删除堆顶元素
     *
     * @return 堆顶元素
     */
    public int poll() {
        int top = array[0];
        swap(0, size - 1);
        size--;
        down(0);
        return top;
    }

    /**
     * 删除指定索引处元素
     *
     * @param index 索引
     * @return 被删除元素
     */
    public int poll(int index) {
        int deleted = array[index];
        swap(index, size - 1);
        size--;
        down(index);
        return deleted;
    }

    /**
     * 替换堆顶元素
     * @param replaced 新元素
     */
    public void replace(int replaced) {
        array[0] = replaced;
        down(0);
    }

    /**
     * 堆的尾部添加元素
     *
     * @param offered 新元素
     * @return 是否添加成功
     */
    public boolean offer(int offered) {
        if (size == array.length) {
            return false;
        }
        up(offered);
        size++;
        return true;
    }

    // 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶
    private void up(int offered) {
        int child = size;
        while (child > 0) {
            int parent = (child - 1) / 2;
            if (offered > array[parent]) {
                array[child] = array[parent];
            } else {
                break;
            }
            child = parent;
        }
        array[child] = offered;
    }

    public MaxHeap(int[] array) {
        this.array = array;
        this.size = array.length;
        heapify();
    }

    // 建堆
    private void heapify() {
        // 如何找到最后这个非叶子节点  size / 2 - 1
        for (int i = size / 2 - 1; i >= 0; i--) {
            down(i);
        }
    }

    // 将 parent 索引处的元素下潜: 与两个孩子较大者交换, 直至没孩子或孩子没它大
    private void down(int parent) {
        int left = parent * 2 + 1;
        int right = left + 1;
        int max = parent;
        if (left < size && array[left] > array[max]) {
            max = left;
        }
        if (right < size && array[right] > array[max]) {
            max = right;
        }
        if (max != parent) { // 找到了更大的孩子
            swap(max, parent);
            down(max);
        }
    }

    // 交换两个索引处的元素
    private void swap(int i, int j) {
        int t = array[i];
        array[i] = array[j];
        array[j] = t;
    }

    public static void main(String[] args) {

        int[] array = {1, 2, 3, 4, 5, 6, 7};
        MaxHeap maxHeap = new MaxHeap(array);
        System.out.println(Arrays.toString(maxHeap.array));
    }
}

建堆

Floyd 建堆算法作者（也是之前龟兔赛跑判环作者）：

基础数据结构_第32张图片

  1. 找到最后一个非叶子节点

  2. 从后向前，对每个节点执行下潜

一些规律

  • 一棵满二叉树节点个数为 $2^h-1$，如下例中高度 $h=3$ 节点数是 $2^3-1=7$

  • 非叶子节点范围为 $[0, size/2-1]$

算法时间复杂度分析

基础数据结构_第33张图片 

 下面看交换次数的推导：设节点高度为 3

本层节点数 高度 下潜最多交换次数（高度-1）
4567 这层 4 1 0
23这层 2 2 1
1这层 1 3 2

每一层的交换次数为：$节点个数*此节点交换次数$，总的交换次数为

基础数据结构_第34张图片

 即

基础数据结构_第35张图片

在 Wolfram|Alpha: Computational Intelligence 输入

Sum[\(40)Divide[Power[2,x],Power[2,i]]*\(40)i-1\(41)\(41),{i,1,x}]

推导出

        

 其中 $2^h \approx n$，$h \approx \log_2{n}$，因此有时间复杂度 $O(n)$

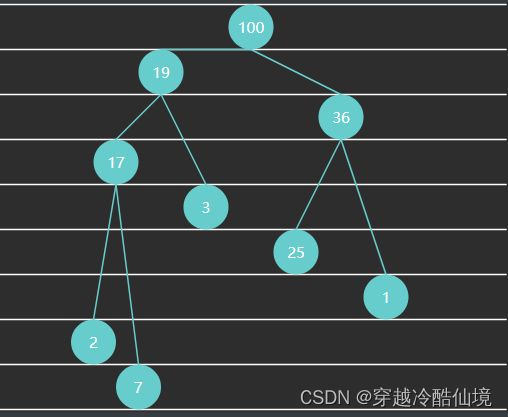
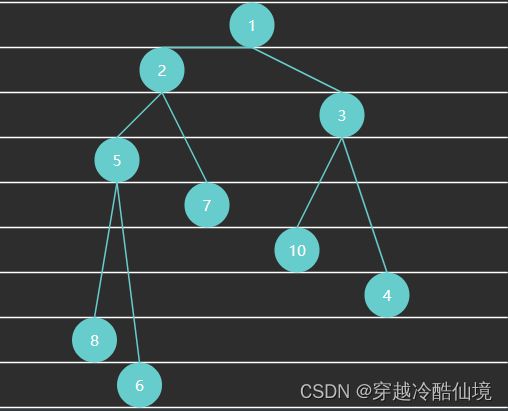
10. 二叉树

二叉树是这么一种树状结构：每个节点最多有两个孩子，左孩子和右孩子

重要的二叉树结构

  • 完全二叉树（complete binary tree）是一种二叉树结构，除最后一层以外，每一层都必须填满，填充时要遵从先左后右

  • 平衡二叉树（balance binary tree）是一种二叉树结构，其中每个节点的左右子树高度相差不超过 1


存储

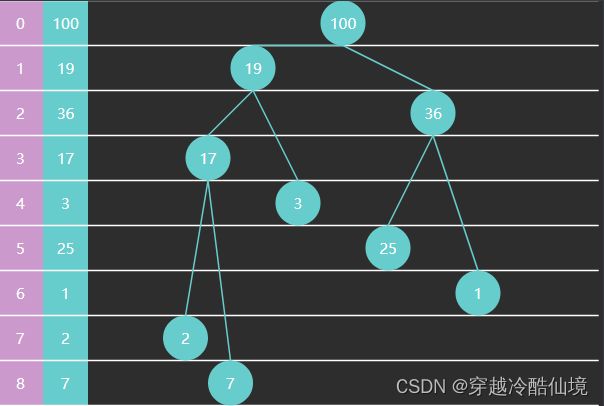
存储方式分为两种

  1. 定义树节点与左、右孩子引用（TreeNode）

  2. 使用数组，前面讲堆时用过，若以 0 作为树的根，索引可以通过如下方式计算

    • 父 = floor((子 - 1) / 2)

    • 左孩子 = 父 * 2 + 1

    • 右孩子 = 父 * 2 + 2

遍历

遍历也分为两种

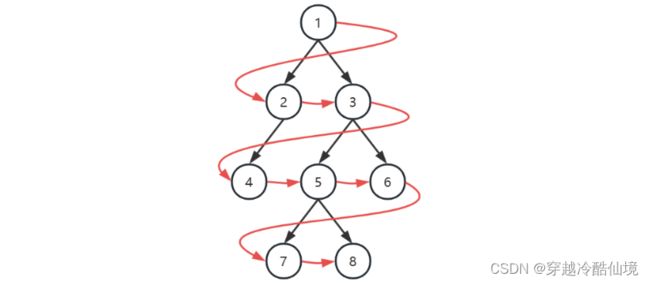
  1. 广度优先遍历（Breadth-first order）：尽可能先访问距离根最近的节点，也称为层序遍历

  2. 深度优先遍历（Depth-first order）：对于二叉树，可以进一步分成三种（要深入到叶子节点）

    1. pre-order 前序遍历，对于每一棵子树，先访问该节点，然后是左子树，最后是右子树

    2. in-order 中序遍历，对于每一棵子树，先访问左子树，然后是该节点，最后是右子树

    3. post-order 后序遍历，对于每一棵子树，先访问左子树，然后是右子树，最后是该节点

广度优先

基础数据结构_第36张图片

 

  1. 初始化，将根节点加入队列

  2. 循环处理队列中每个节点，直至队列为空

  3. 每次循环内处理节点后，将它的孩子节点（即下一层的节点）加入队列

注意

  • 以上用队列来层序遍历是针对 TreeNode 这种方式表示的二叉树

  • 对于数组表现的二叉树，则直接遍历数组即可，自然为层序遍历的顺序

深度优先

基础数据结构_第37张图片

 

递归实现

/**
 * 
前序遍历

 * @param node 节点
 */
static void preOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    System.out.print(node.val + "\t"); // 值
    preOrder(node.left); // 左
    preOrder(node.right); // 右
}

/**
 * 
中序遍历

 * @param node 节点
 */
static void inOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    inOrder(node.left); // 左
    System.out.print(node.val + "\t"); // 值
    inOrder(node.right); // 右
}

/**
 * 
后序遍历

 * @param node 节点
 */
static void postOrder(TreeNode node) {
    if (node == null) {
        return;
    }
    postOrder(node.left); // 左
    postOrder(node.right); // 右
    System.out.print(node.val + "\t"); // 值
}

非递归实现

前序遍历

LinkedListStack stack = new LinkedListStack<>();
TreeNode curr = root;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        System.out.println(curr);
        curr = curr.left;
    } else {
        TreeNode pop = stack.pop();
        curr = pop.right;
    }

}

 

中序遍历

LinkedListStack stack = new LinkedListStack<>();
TreeNode curr = root;

while (!stack.isEmpty() || curr != null) {
    if (curr != null) {
        stack.push(curr);
        curr = curr.left;
    } else {
        TreeNode pop = stack.pop();
        System.out.println(pop);
        curr = pop.right;
    }
}

后序遍历

对于后序遍历，向回走时，需要处理完右子树才能 pop 出栈。如何知道右子树处理完成呢？

  • 如果栈顶元素的 $right \equiv null$ 表示没啥可处理的，可以出栈

  • 如果栈顶元素的 $right \neq null$，

    • 那么使用 lastPop 记录最近出栈的节点，即表示从这个节点向回走

    • 如果栈顶元素的 $right==lastPop$ 此时应当出栈

对于前、中两种遍历，实际以上代码从右子树向回走时，并未走完全程（stack 提前出栈了）后序遍历以上代码是走完全程了

统一写法

下面是一种统一的写法，依据后序遍历修改

LinkedList stack = new LinkedList<>();

TreeNode curr = root; // 代表当前节点
TreeNode pop = null; // 最近一次弹栈的元素
while (curr != null || !stack.isEmpty()) {
    if (curr != null) {
        colorPrintln("前: " + curr.val, 31);
        stack.push(curr); // 压入栈，为了记住回来的路
        curr = curr.left;
    } else {
        TreeNode peek = stack.peek();
        // 右子树可以不处理, 对中序来说, 要在右子树处理之前打印
        if (peek.right == null) {
            colorPrintln("中: " + peek.val, 36);
            pop = stack.pop();
            colorPrintln("后: " + pop.val, 34);
        }
        // 右子树处理完成, 对中序来说, 无需打印
        else if (peek.right == pop) {
            pop = stack.pop();
            colorPrintln("后: " + pop.val, 34);
        }
        // 右子树待处理, 对中序来说, 要在右子树处理之前打印
        else {
            colorPrintln("中: " + peek.val, 36);
            curr = peek.right;
        }
    }
}

public static void colorPrintln(String origin, int color) {
    System.out.printf("\033[%dm%s\033[0m%n", color, origin);
}

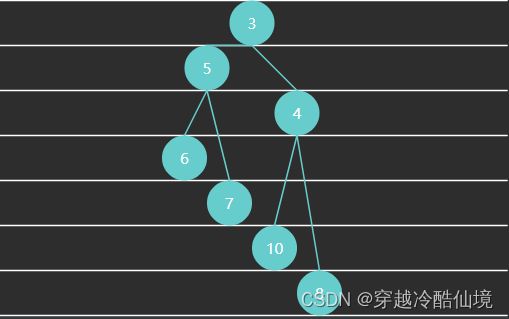
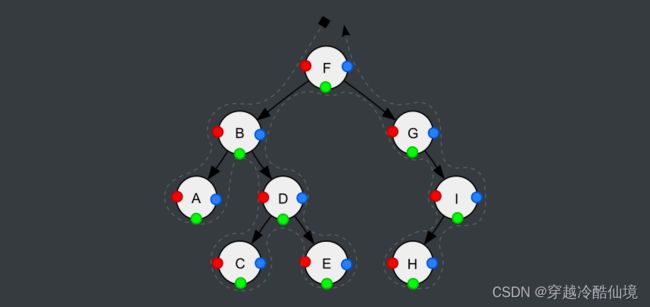
一张图演示三种遍历

基础数据结构_第38张图片

 

  • 红色：前序遍历顺序

  • 绿色：中序遍历顺序

  • 蓝色：后续遍历顺序

你可能感兴趣的:(算法,数据结构)

  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • Goolge earth studio 进阶4——路径修改与平滑 陟彼高冈yu Googleearthstudio进阶教程旅游
    如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
  • 基于社交网络算法优化的二维最大熵图像分割 智能算法研学社（Jack旭） 智能优化算法应用图像分割算法php开发语言
    智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
  • 数组去重 好奇的猫猫猫
    整理自js中基础数据结构数组去重问题思考？如何去除数组中重复的项例如数组：[1,3,4,3,5]我们在做去重的时候，一开始想到的肯定是，逐个比较，外面一层循环，内层后一个与前一个一比较，如果是久不将当前这一项放进新的数组，挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低，代码量还多，思考？有没有更好的方法这时候不禁一想当然有了！！！hashtable啊，通过对象的hash办法
  • 121. 买卖股票的最佳时机 薄荷糖的味道_fb40
    给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
  • 每日算法&面试题，大厂特训二十八天——第二十天（树） 肥学 ⚡算法题⚡面试题每日精进java算法数据结构
    目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
  • 回溯算法-重新安排行程 chirou_ 算法数据结构图论c++图搜索
    leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
  • Redis系列：Geo 类型赋能亿级地图位置计算 Ly768768 redisbootstrap数据库
    1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构，它是基于不同业务场景而设计的：动态字符串(REDIS_STRING)：整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
  • Faiss：高效相似性搜索与聚类的利器 网络·魚 大数据faiss
    Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
  • 数据结构之哈希表 X同学的开始 数据结构数据结构散列表
    哈希表(散列表)出现的原因在顺序表中查找时，需要从表头开始，依次遍历比较a[i]与key的值是否相等，直到相等才返回索引i；在有序表中查找时，我们经常使用的是二分查找，通过比较key与a[i]的大小来折半查找，直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是，这两种方法的效率都依赖于查找中比较的次数。我们有一种想法，能不能不经过比较，而是直接通过关键字key一次得到所要的结果呢？这时，
  • insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insertintoselect主键自增mybatisdelete返回值mybatisinsert返回主键mybatisinsert返回对象mybatisplusinsert返回主键mybatisplus插入生成id
    前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
  • k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
    ?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
  • Python开发常用的三方模块如下： 换个网名有点难 python开发语言
    Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
  • Python实现简单的机器学习算法 master_chenchengg pythonpython办公效率python开发IT
    Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
  • 推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
    importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
  • K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习K近邻
    importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
  • 数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列C语言
    文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
  • [Python] 数据结构 详解及代码 AIAdvocate 算法python数据结构链表
    今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
  • 4.C_数据结构_队列 荣世蓥 数据结构数据结构
    概述什么是队列：队列是限定在两端进行插入操作和删除操作的线性表。具有先入先出(FIFO)的特点相关名词：队尾：写入数据的一段队头：读取数据的一段空队：队列中没有数据，队头指针=队尾指针满队：队列中存满了数据，队尾指针+1=队头指针循环队列1、基本内容循环队列是以数组形式构成的队列数据结构。循环队列的结构体如下：typedefintdata_t;//队列数据类型#defineN64//队列容量typ
  • Python算法L5：贪心算法 小熊同学哦 Python算法算法python贪心算法
    Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
  • C++八股 Petrichorzncu 八股总结c++开发语言
    这里写目录标题C++内存管理C++的构造函数，复制构造函数，和析构函数深复制与浅复制：构造函数和析构函数哪个能写成虚函数，为什么？C++数据结构内存排列结构体和类占用的内存：==虚函数和虚表的原理==虚函数虚表（Vtable）虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
  • 【RabbitMQ 项目】服务端：数据管理模块之绑定管理 月夜星辉雪 rabbitmq分布式
    文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字：交换机的路由交换算法中会用到没有是否持久化的标志，因为绑定是否持久化取决于交换机和队列是否持久化，只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子，两端连接着交换机和队列，当一方不存在，它就没有存在的必要了定义绑定持久化类构造函数：如果数据库文件不存在则创建，打开数据库，创建binding_table插入
  • 【树一线性代数】005入门 Owlet_woodBird 算法
    Index本文稍后补全，推荐阅读：https://blog.csdn.net/weixin_60702024/article/details/141874376分析实现总结本文稍后补全，推荐阅读：https://blog.csdn.net/weixin_60702024/article/details/141874376已知非空二叉树T的结点值均为正整数，采用顺序存储方式保存，数据结构定义如下:t
  • python获取子进程返回值_Python对进程Multiprocessing子进程返回值 weixin_39752157 python获取子进程返回值
    在实际使用多进程的时候，可能需要获取到子进程运行的返回值。如果只是用来存储，则可以将返回值保存到一个数据结构中；如果需要判断此返回值，从而决定是否继续执行所有子进程，则会相对比较复杂。另外在Multiprocessing中，可以利用Process与Pool创建子进程，这两种用法在获取子进程返回值上的写法上也不相同。这篇中，我们直接上代码，分析多进程中获取子进程返回值的不同用法，以及优缺点。初级用法
  • 非对称加密算法原理与应用2——RSA私钥加密文件 私语茶馆 云部署与开发架构及产品灵感记录RSA2048私钥加密
    作者：私语茶馆1.相关章节（1）非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对，并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容，包括从密钥库或文件中读取私钥，并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件，只能由该私钥对应的公钥来解密。
  • 【数据结构-一维差分】力扣2848. 与车相交的点 hlc@ 数据结构数据结构leetcode算法
    给你一个下标从0开始的二维整数数组nums表示汽车停放在数轴上的坐标。对于任意下标i，nums[i]=[starti,endi]，其中starti是第i辆车的起点，endi是第i辆车的终点。返回数轴上被车任意部分覆盖的整数点的数目。示例1：输入：nums=[[3,6],[1,5],[4,7]]输出：7解释：从1到7的所有点都至少与一辆车相交，因此答案为7。示例2：输入：nums=[[1,3],[5
  • 粒子群优化 (PSO) 在三维正弦波函数中的应用 subject625Ruben 机器学习人工智能matlab算法
    在这篇博客中，我们将展示如何使用粒子群优化（PSO）算法求解三维正弦波函数，并通过增加正弦波扰动，使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程，并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数，定义如下：objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
  • JavaScript `Map` 和 `WeakMap`详细解释 跳房子的前端 JavaScript原生方法javascript前端开发语言
    在JavaScript中，Map和WeakMap都是用于存储键值对的数据结构，但它们有一些关键的不同之处。MapMap是一种可以存储任意类型的键值对的集合。它保持了键值对的插入顺序，并且可以通过键快速查找对应的值。Map提供了一些非常有用的方法和属性来操作这些数据对：set(key,value):将一个键值对添加到Map中。如果键已经存在，则更新其对应的值。get(key):获取指定键的值。如果键
  • 非对称加密算法————RSA理论及详情 hu19930613
    转自：https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前，所有的加密方法都是同一种模式：（1）甲方选择某一种加密规则，对信息进行加密；（2）乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-keyalgorithm）。这种加密模式有一个最大弱点
  • ai绘画工具midjourney怎么下载？附作品管理教程 设计师早上好
    Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
  • 插入表主键冲突做更新 a-john
    有以下场景： 用户下了一个订单，订单内的内容较多，且来自多表，首次下单的时候，内容可能会不全（部分内容不是必须，出现有些表根本就没有没有该订单的值）。在以后更改订单时，有些内容会更改，有些内容会新增。 问题： 如果在sql语句中执行update操作，在没有数据的表中会出错。如果在逻辑代码中先做查询，查询结果有做更新，没有做插入，这样会将代码复杂化。 解决： mysql中提供了一个sql语
  • Android xml资源文件中@、@android:type、@*、？、@+含义和区别 Cb123456 @+@?@*
    一.@代表引用资源 1.引用自定义资源。格式：@[package:]type/name android：text="@string/hello"   2.引用系统资源。格式：@android:type/name     android:textColor="@android:color/opaque_red"
  • 数据结构的基本介绍 天子之骄 数据结构散列表树、图线性结构价格标签
    数据结构的基本介绍 数据结构就是数据的组织形式，用一种提前设计好的框架去存取数据，以便更方便，高效的对数据进行增删查改。正确选择合适的数据结构，对软件程序的高效执行的影响作用不亚于算法的设计。此外，在计算机系统中数据结构的作用也是非同小可。例如常常在编程语言中听到的栈，堆等，就是经典的数据结构。   经典的数据结构大致如下：   一：线性数据结构 (1)：列表 a
  • 通过二维码开放平台的API快速生成二维码 一炮送你回车库 api
     现在很多网站都有通过扫二维码用手机连接的功能，联图网(http://www.liantu.com/pingtai/)的二维码开放平台开放了一个生成二维码图片的Api,挺方便使用的。闲着无聊，写了个前台快速生成二维码的方法。        html代码如下:(二维码将生成在这div下) ? 1  &nbs
  • ImageIO读取一张图片改变大小 3213213333332132 javaIOimageBufferedImage
    package com.demo; import java.awt.image.BufferedImage; import java.io.File; import java.io.IOException; import javax.imageio.ImageIO; /** * @Description 读取一张图片改变大小 * @author FuJianyon
  • myeclipse集成svn（一针见血） 7454103 eclipseSVNMyEclipse
                                     &n
  • 装箱与拆箱----autoboxing和unboxing darkranger J2SE
    4.2　自动装箱和拆箱 基本数据(Primitive)类型的自动装箱(autoboxing)、拆箱(unboxing)是自J2SE 5.0开始提供的功能。虽然为您打包基本数据类型提供了方便，但提供方便的同时表示隐藏了细节，建议在能够区分基本数据类型与对象的差别时再使用。 4.2.1　autoboxing和unboxing 在Java中，所有要处理的东西几乎都是对象(Object)
  • ajax传统的方式制作ajax aijuans Ajax
    //这是前台的代码 <%@ page language="java" import="java.util.*" pageEncoding="UTF-8"%> <% String path = request.getContextPath(); String basePath = request.getScheme()+
  • 只用jre的eclipse是怎么编译java源文件的？ avords javaeclipsejdktomcat
    eclipse只需要jre就可以运行开发java程序了，也能自动 编译java源代码，但是jre不是java的运行环境么，难道jre中也带有编译工具？ 还是eclipse自己实现的？谁能给解释一下呢问题补充：假设系统中没有安装jdk or jre，只在eclipse的目录中有一个jre，那么eclipse会采用该jre，问题是eclipse照样可以编译java源文件，为什么呢？ &nb
  • 前端模块化 bee1314 模块化
    背景： 前端JavaScript模块化，其实已经不是什么新鲜事了。但是很多的项目还没有真正的使用起来，还处于刀耕火种的野蛮生长阶段。   JavaScript一直缺乏有效的包管理机制，造成了大量的全局变量，大量的方法冲突。我们多么渴望有天能像Java（import），Python (import)，Ruby(require)那样写代码。在没有包管理机制的年代，我们是怎么避免所
  • 处理百万级以上的数据处理 bijian1013 oraclesql数据库大数据查询
    一.处理百万级以上的数据提高查询速度的方法：        1.应尽量避免在 where 子句中使用!=或<>操作符，否则将引擎放弃使用索引而进行全表扫描。         2.对查询进行优化，应尽量避免全表扫描，首先应考虑在 where 及 o
  • mac 卸载 java 1.7 或更高版本 征客丶 javaOS
    卸载 java 1.7 或更高 sudo rm -rf /Library/Internet\ Plug-Ins/JavaAppletPlugin.plugin 成功执行此命令后，还可以执行 java 与 javac 命令 sudo rm -rf /Library/PreferencePanes/JavaControlPanel.prefPane 成功执行此命令后，还可以执行 java
  • 【Spark六十一】Spark Streaming结合Flume、Kafka进行日志分析 bit1129 Stream
    第一步，Flume和Kakfa对接，Flume抓取日志，写到Kafka中 第二部，Spark Streaming读取Kafka中的数据，进行实时分析   本文首先使用Kakfa自带的消息处理（脚本）来获取消息，走通Flume和Kafka的对接 1. Flume配置 1. 下载Flume和Kafka集成的插件，下载地址：https://github.com/beyondj2ee/f
  • Erlang vs TNSDL bookjovi erlang
          TNSDL是Nokia内部用于开发电信交换软件的私有语言，是在SDL语言的基础上加以修改而成，TNSDL需翻译成C语言得以编译执行，TNSDL语言中实现了异步并行的特点，当然要完整实现异步并行还需要运行时动态库的支持，异步并行类似于Erlang的process（轻量级进程），TNSDL中则称之为hand，Erlang是基于vm(beam)开发，
  • 非常希望有一个预防疲劳的java软件, 预防过劳死和眼睛疲劳,大家一起努力搞一个 ljy325 企业应用
    　非常希望有一个预防疲劳的java软件，我看新闻和网站，国防科技大学的科学家累死了，太疲劳，老是加班，不休息，经常吃药，吃药根本就没用，根本原因是疲劳过度。我以前做java,那会公司垃圾，老想赶快学习到东西跳槽离开，搞得超负荷，不明理。深圳做软件开发经常累死人，总有不明理的人，有个软件提醒限制很好，可以挽救很多人的生命。 相关新闻： （1）IT行业成五大疾病重灾区：过劳死平均37.9岁
  • 读《研磨设计模式》-代码笔记-原型模式 bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ /** * Effective Java 建议使用copy constructor or copy factory来代替clone()方法： * 1.public Product copy(Product p){} * 2.publi
  • 配置管理---svn工具之权限配置 chenyu19891124 SVN
    今天花了大半天的功夫，终于弄懂svn权限配置。下面是今天收获的战绩。 安装完svn后就是在svn中建立版本库，比如我本地的是版本库路径是C:\Repositories\pepos。pepos是我的版本库。在pepos的目录结构 pepos    component    webapps 在conf里面的auth里赋予的权限配置为 [groups]
  • 浅谈程序员的数学修养 comsci 设计模式编程算法面试招聘
                                     浅谈程序员的数学修养
  • 批量执行 bulk collect与forall用法 daizj oraclesqlbulk collectforall
    BULK COLLECT 子句会批量检索结果，即一次性将结果集绑定到一个集合变量中，并从SQL引擎发送到PL/SQL引擎。通常可以在SELECT INTO、 FETCH INTO以及RETURNING INTO子句中使用BULK COLLECT。本文将逐一描述BULK COLLECT在这几种情形下的用法。     有关FORALL语句的用法请参考：批量SQL之 F
  • Linux下使用rsync最快速删除海量文件的方法 dongwei_6688 OS
    1、先安装rsync：yum install rsync 2、建立一个空的文件夹：mkdir /tmp/test 3、用rsync删除目标目录：rsync --delete-before -a -H -v --progress --stats /tmp/test/ log/这样我们要删除的log目录就会被清空了，删除的速度会非常快。rsync实际上用的是替换原理，处理数十万个文件也是秒删。
  • Yii CModel中rules验证规格 dcj3sjt126com rulesyiivalidate
    Yii cValidator主要用法分析：  yii验证rulesit 分类： Yii yii的rules验证 cValidator主要属性 attributes ,builtInValidators,enableClientValidation,message,on,safe,skipOnError  
  • 基于vagrant的redis主从实验 dcj3sjt126com vagrant
    平台: Mac 工具: Vagrant 系统: Centos6.5 实验目的: Redis主从   实现思路 制作一个基于sentos6.5, 已经安装好reids的box, 添加一个脚本配置从机, 然后作为后面主机从机的基础box   制作sentos6.5+redis的box   mkdir vagrant_redis cd vagrant_
  • Memcached(二)、Centos安装Memcached服务器 frank1234 centosmemcached
    一、安装gcc rpm和yum安装memcached服务器连接没有找到，所以我使用的是make的方式安装，由于make依赖于gcc，所以要先安装gcc 开始安装，命令如下，[color=red][b]顺序一定不能出错[/b][/color]： 建议可以先切换到root用户，不然可能会遇到权限问题：su root 输入密码...... rpm -ivh kernel-head
  • Remove Duplicates from Sorted List hcx2013 remove
    Given a sorted linked list, delete all duplicates such that each element appear only once. For example,Given 1->1->2, return 1->2.Given 1->1->2->3->3, return&
  • Spring4新特性——JSR310日期时间API的支持 jinnianshilongnian spring4
    Spring4新特性——泛型限定式依赖注入 Spring4新特性——核心容器的其他改进 Spring4新特性——Web开发的增强 Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC  Spring4新特性——Groovy Bean定义DSL Spring4新特性——更好的Java泛型操作API  Spring4新
  • 浅谈enum与单例设计模式 247687009 java单例
    在JDK1.5之前的单例实现方式有两种(懒汉式和饿汉式并无设计上的区别故看做一种)，两者同是私有构 造器，导出静态成员变量，以便调用者访问。 第一种 package singleton; public class Singleton { //导出全局成员 public final static Singleton INSTANCE = new S
  • 使用switch条件语句需要注意的几点 openwrt cbreakswitch
    1. 当满足条件的case中没有break，程序将依次执行其后的每种条件（包括default）直到遇到break跳出 int main() { int n = 1; switch(n) { case 1: printf("--1--\n"); default: printf("defa
  • 配置Spring Mybatis JUnit测试环境的应用上下文 schnell18 springmybatisJUnit
    Spring-test模块中的应用上下文和web及spring boot的有很大差异。主要试下来差异有： 单元测试的app context不支持从外部properties文件注入属性 @Value注解不能解析带通配符的路径字符串 解决第一个问题可以配置一个PropertyPlaceholderConfigurer的bean。 第二个问题的具体实例是：    
  • Java 定时任务总结一 tuoni javaspringtimerquartztimertask
     Java定时任务总结  一.从技术上分类大概分为以下三种方式：  1.Java自带的java.util.Timer类，这个类允许你调度一个java.util.TimerTask任务;   说明：    java.util.Timer定时器，实际上是个线程，定时执行TimerTask类 &
  • 一种防止用户生成内容站点出现商业广告以及非法有害等垃圾信息的方法 yangshangchuan rank相似度计算文本相似度词袋模型余弦相似度
    本文描述了一种在ITEYE博客频道上面出现的新型的商业广告形式及其应对方法，对于其他的用户生成内容站点类型也具有同样的适用性。   最近在ITEYE博客频道上面出现了一种新型的商业广告形式，方法如下：     1、注册多个账号（一般10个以上）。     2、从多个账号中选择一个账号，发表1-2篇博文
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他