深入探索JavaScript中的5种经典算法
在本文中,您将了解到:
冒泡排序、快速排序等常见排序算法原理及其在 JavaScript 中的实现;
经典算法示例
1. 冒泡排序算法
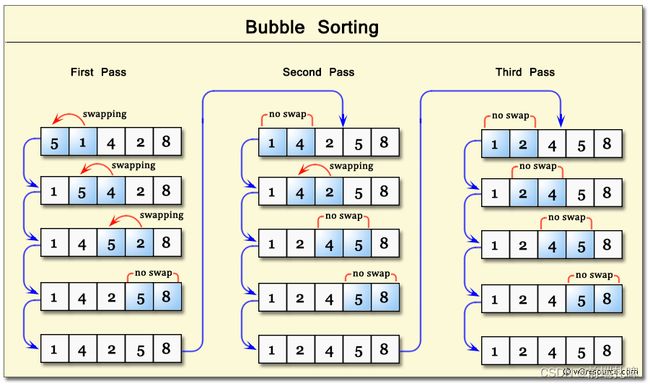
冒泡排序算法:冒泡排序是一种简单但效率较低的排序算法。它通过多次遍历数组,比较相邻元素并交换位置来实现排序。
原理图示
js实现
function bubbleSort(arr) {
const len = arr.length;
for (let i = 0; i < len - 1; i++) {
// 每次遍历比较相邻元素并交换位置,将最大的元素移到末尾
for (let j = 0; j < len - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 使用解构赋值进行元素交换
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
}
return arr;
}
// 示例用法:
const numbers = [4, 2, 6, 8, 3];
console.log(bubbleSort(numbers)); // 输出: [2,3,4,6,8]
bubbleSort 函数接受一个数组作为参数,并使用嵌套循环遍历数组来执行冒泡排序。内部循环通过比较相邻元素并根据需要交换它们的位置来实现排序。外部循环控制总共要进行多少轮排序操作。
2. 快速排序算法
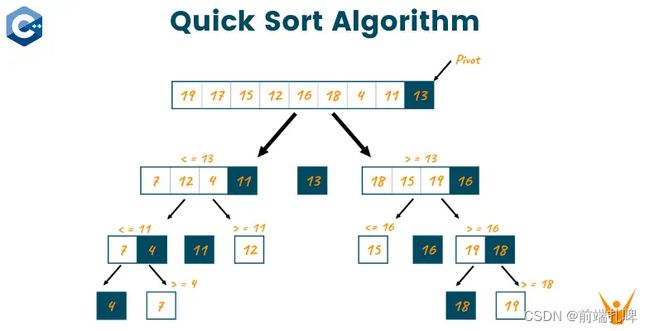
快速排序算法:快速排序是一种高效的分治算法。它选择一个基准元素,并将数组分成两个子数组,其中一个小于基准值,另一个大于基准值。然后递归地对这两个子数组进行快速排序。
原理图示
js实现
function quickSort(arr) {
if (arr.length <= 1) {
return arr;
}
const pivot = arr[Math.floor(arr.length / 2)]; // 选择数组中间元素作为基准值
const left = [];
const right = [];
for (let i =0; i<arr.length;i++){
if(i!== Math.floor(arr.length/2)){
if(arr[i]<pivot){
left.push(arr[i]);
} else{
right.push(arr[i]);
}
}
}
return [...quickSort(left),pivot,...quickSort(right)];
}
// 示例用法:
const numbers = [4, 2, -3, 6, -8];
console.log(quickSort(numbers)); // 输出: [-8,-3,2,4,6]
quickSort 函数接受一个数组作为参数,并通过递归方式实现快速排序。首先选择数组中间的元素作为基准值(也可以选择其他位置),然后将小于基准值的元素放入左侧数组 left,大于等于基准值的元素放入右侧数组 right。最后,使用递归调用对左右子数组进行快速排序,并合并结果。
3. 二分查找算法
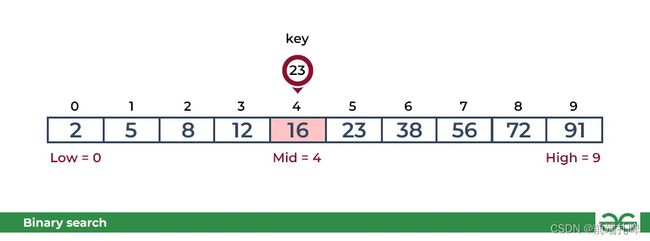
二分查找算法:二分查找是在有序数组中查找特定元素的常用方法。它通过将目标值与数组中间元素进行比较,并根据比较结果缩小搜索范围直到找到目标值或确定不存在。
原理图示
js实现
function binarySearch(arr, target) {
let left = 0;
let right = arr.length - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
if (arr[mid] === target) {
return mid; // 找到目标元素,返回索引位置
} else if (arr[mid] < target) {
left = mid + 1; // 目标在右侧子数组中
} else {
right = mid - 1; // 目标在左侧子数组中
}
}
return -1; // 没有找到目标元素,返回-1表示失败
}
// 示例用法:
const numbers = [2, 4, 6, 8,10];
console.log(binarySearch(numbers,6)); // 输出: 2
binarySearch 函数接受一个已排序的数组 arr 和目标值 target。通过不断将搜索范围缩小至左半部分或右半部分来实现二分查找。
4. 阶乘函数
阶乘函数用于计算给定数字 n 的阶乘(n!)。递归和迭代都可以实现该功能。
原理图示
js实现
function factorial(n) {
if (n === 0 || n === 1) {
return 1; // 当输入为0或1时,直接返回1
} else {
return n * factorial(n - 1); // 使用递归计算阶乘
}
}
// 示例用法:
console.log(factorial(5)); // 输出: 120
factorial 函数接受一个非负整数 n 参数,并通过递归方式计算其阶乘。当输入值为0或1时,直接返回结果为1;否则,在每一次递归调用过程中,将当前参数 n 和 n-1 相乘。重复这个过程直到 n 值减至0或者1。
5. 斐波那契数列
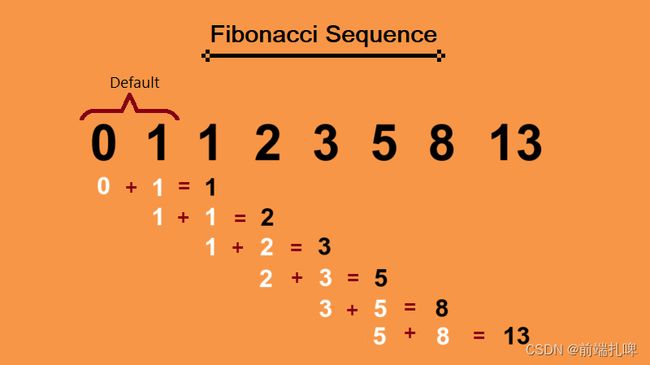
斐波那契数列:斐波那契数列是由前两个数字开始,并且每个后续数字都等于前两个数字之和的序列。使用递归或循环方法都可以生成斐波那契数列。
原理图示
js实现
function fibonacci(n) {
if (n === 0) {
return 0; // 当输入为0时,直接返回0
} else if (n === 1 || n === 2) {
return 1; // 当输入为1或2时,直接返回1
} else {
let a = 1;
let b = 1;
for (let i = 3; i <= n; i++) {
const temp = a + b;
a = b;
b = temp;
}
return b; // 返回第n个斐波那契数列的值
}
}
// 示例用法:
console.log(fibonacci(6)); // 输出:8
fibonacci 函数接受一个非负整数 n 参数,并通过迭代方式计算其对应位置上的斐波那契数。当输入值为0时,直接返回结果为0;当输入值为1或2时,也直接返回结果为1;否则,在每一次迭代过程中利用两个变量 a 和 b 来保存当前位置和前一个位置的斐波那契数。通过不断更新这两个变量来求解下一个位置上的斐波那契数。
总结
算法的使用意义:
- 提高性能:使用高效的算法可以提升程序的执行效率。例如,对大型数据集进行排序时,使用快速排序比简单的冒泡或选择排序更有效率。
- 数据处理与查询:搜索算法允许我们在给定数据集中查找特定元素。例如,通过二分查找可以快速地在已经排好序的数组中查找目标值。
- 优化资源利用:某些问题可能存在重复计算或者多次使用相同结果的情况。递归和动态规划是解决这类问题非常有用的方法。它们可以帮助我们避免重复计算,并且将问题拆解为子问题来求解,从而节省时间和资源。
- 程序设计思维培养:学习和理解常见算法可以培养抽象化思考能力以及良好的程序设计习惯。熟悉各种类型的问题并掌握相应的解决方案,有助于编写清晰且可扩展性高的代码。
- 面试和竞争力:在面试过程中,算法问题是常见的考察点。掌握常见算法并能够灵活运用,可以提升求职竞争力,并展示自己的技术水平。