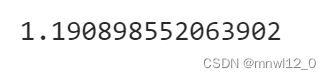量化交易全流程（二）
本节目录：
--------------------------------------------统计分析基础--------------------------------------------
基本统计概念：
随机数和分布：
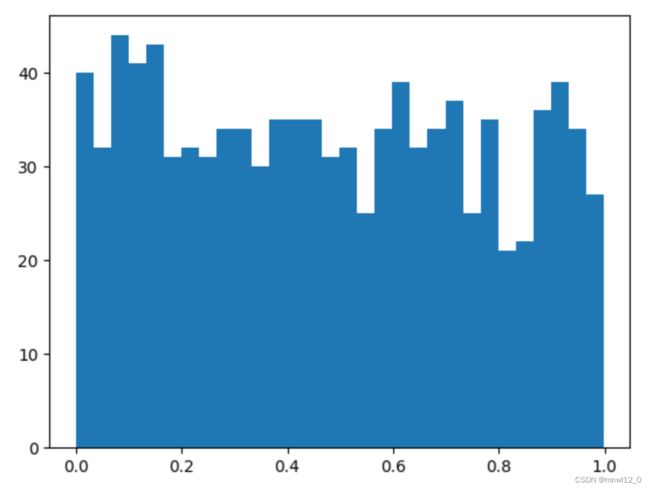
1、rand和random_sample，两者都是均匀分布的产生随机数生成函数，功能基本一致，rand函数传入多个整数参数作为生成数组的维度，random_sample传入一个n维元组元素作为参数，一般推荐使用random_sample，如以下代码：
import numpy as np
import matplotlib.pyplot as plt
data_uni=np.random.random_sample((1000))
plt.hist(data_uni,bins=30)
plt.show()
2、randn和standard_normal
randn和standard_normal都是生成正态分布的随机数生成函数，传入参数类似于rand和random_sample，通常用standard_normal：
import numpy as np
import matplotlib.pyplot as plt
data_normal=np.random.standard_normal((1000))
plt.hist(data_normal,bins=30)
plt.show()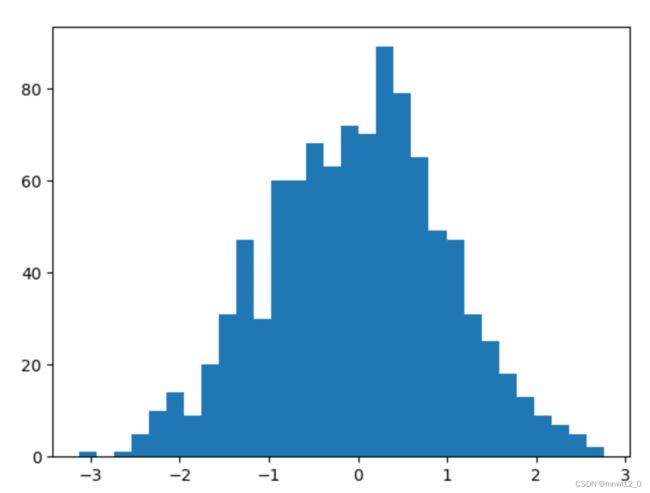
从正态分布中取样，取出一个大小为10维的一维数组，可以使用:
data=np.random.randn(10)
3、randint和random_integers
都是均匀分布的整数生成函数，一般传入三个参数：low，high，size，两者区别在于randint范围不包括最大值，而random_integers包括最大值，（即包不包含右区间的值）：
x1=np.random.randint(1,10,(100))
print(x1.max())
x2=np.random.random_integers(1,10,(100))
x2.max()
4、shuffle
可以随机打乱一个数组，并且改变此数组的本身排列：
x=np.arange(10)
print(x)
np.random.shuffle(x) #不能赋值给x，无法赋值
x
5、Premutation
返回一个打乱顺序后的数组值，但并不会改变传入参数数组本身：
x=np.arange(10)
print(x)
y=np.random.permutation(x) #不能赋值给x，无法赋值
y
6、二项式分布binomial(1,p)与binomial(1,p,n)
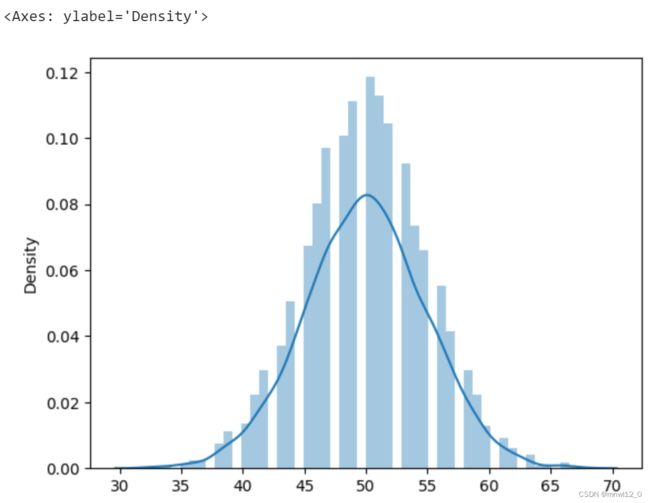
N次伯努利实验结果分布即为二项分布，用binomial(1,p)即为一次二项分布，binomial(1,p,n)即为n维二项分布数组：
import seaborn as sns
x1=np.random.binomial(100,0.5,10000)
sns.distplot(x1)
7、β分布（较抽象，看不懂可跳过）
考虑二项分布的分布函数：
边缘分布存在的意义就在于让后验分布成为一个满足概率定义的数值，先验概率的已知导致仅仅只要通过较小数据量更新即可，避免了过度拟合数据的问题。
预估参数与组合运算项
无关，只与后面概率式有关，可以猜想：假设先验概率也是与概率式有关的分布
，那么后验分布则只要在概率式
前面乘以一个正则项就可以获得一个后验分布，与二项分布有关的共轭分布就是β分布。
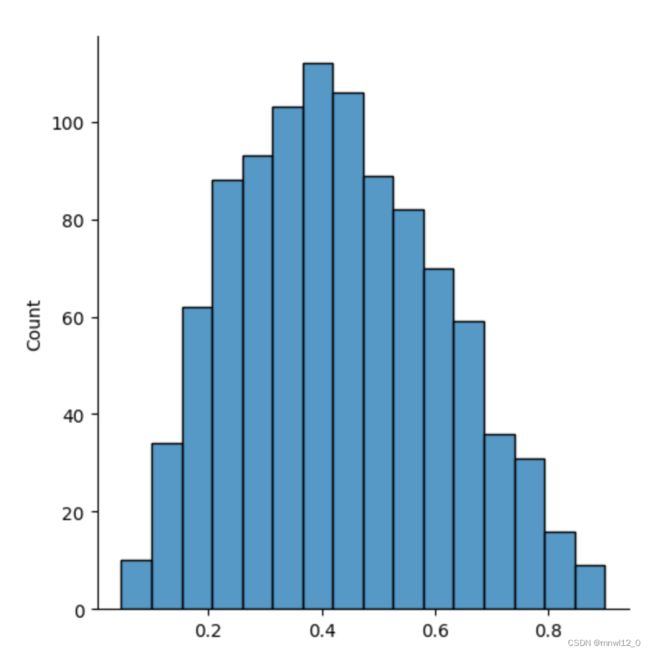
beta(a,b)从Beta(a,b)分布中生成一个随机数，Beta(a,b)、rsv(n)生成一个n维数组，每个数组都是Beta(a,b)分布中随机数。
import seaborn as sns
from scipy import stats
beta=stats.beta(3,4).rvs(1000)
sns.displot(beta)
随机数种子
计算机随即生成的随机数并不是真正的随机数，而是使用特定算法生成的伪随机数，这样会面临两个问题：
1. 如果初始值一样，嘛呢按照相同算法得到的随机数应该也一样，这样不表现随机效果。
2. 很多随机试验需要再现之前结果，因此需要重复之前随机数。
因此在生成随机数之前设定一个种子，种子一样则每次随机数生成结果一样，在numpy里面，随机数的种子用seed设立：
np.random.seed() #空种子
np.random.randn() #首先生成
np.random.seed()
np.random.randn() #再次生成会变
np.random.seed(1) #初始种子
np.random.randn() #首先生成
np.random.seed(1)
np.random.randn() #再次生成不变相关系数
两个随机变量其斜率就是相关系数，相关系数也和协方差有关系：
cov(x,y)=E(x-E(x))(y-E(y))
x=np.random.normal(size=1000)
y=0.5*x+0.5*np.random.normal(size=1000)
np.cov(x,y)
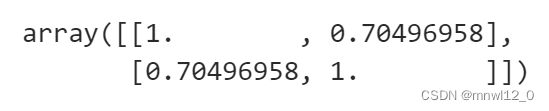
皮尔逊相关系数剔除了量纲上面的影响：
corr(x,y)=cov(x,y)/δxδy，
x=np.random.normal(size=1000)
y=0.5*x+0.5*np.random.normal(size=1000)
np.corrcoef(x,y)
只要两个变量存在相关关系，其相关系数就不会为0.
基本统计量
利用数据的函数变化，从某种维度来反映全体数据集的特征的一种函数
1、mean既可以做函数调用也可作数组方法调用
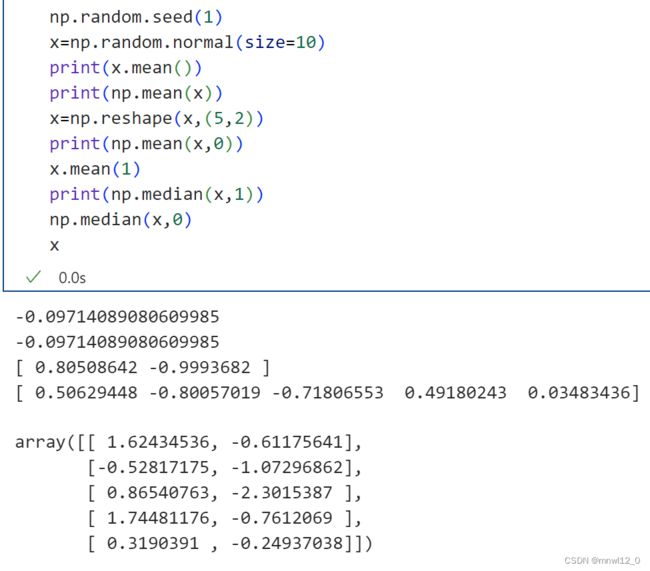
np.random.seed(1)
x=np.random.normal(size=10)
print(x.mean())
print(np.mean(x))
x=np.reshape(x,(5,2))
print(np.mean(x,0))
x.mean(1)
2、median计算中位数，第二个参数是选择维度，既可以做函数调用也可作数组方法调用
median(x,1)
median(x,0)
std
计算标准差
x.std()
var
计算方差
x.var()
随机变量分布：