区间问题与离散化
在竞赛中,我们常遇到对区间进行操作的问题,比如区间类动态规划。这类题目通常数据范围很大,操作看似很简单但是模拟1000%会超时…这时离散化的思想就是解决这类问题的最好方法(你可能会说,许多问题可以用线段树。但是谁愿意放弃短短几行的代码而花十几分钟甚至几十分钟写线段树呢)。
例题1
【问题描述】(NOIp2005普及组P2)
某校大门外长度为L的马路上有一排树,每两棵相邻的树之间的间隔都是1米。我们可以把马路看
成一个数轴,马路的一端在数轴0的位置,另一端在L的位置;数轴上的每个整数点,即0,
1
,
2
,……,
L,都种有一棵树。
由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一
区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括
区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树。
【输入文件】
输入文件tree.in的第一行有两个整数L(
1
<=
L
<=
10000
)和 M(
1
<=
M
<=
100
),
L代表马路的长度,M代表区域的数目,L和M之间用一个空格隔开。接下来的M行每行包含两个不同的整
数,用一个空格隔开,表示一个区域的起始点和终止点的坐标。
【输出文件】
输出文件tree.out包括一行,这一行只包含一个整数,表示马路上剩余的树的数目。
【样例输入】
500
3
150
300
100
200
470
471
【样例输出】
298
【数据规模】
对于20
%
的数据,区域之间没有重合的部分;
对于其它的数据,区域之间有重合的情况。
这道题就不用说了吧,解法很多,最简单的就是开一个标记数组,把所有覆盖的区段标记,最后只要统计标记了多少个数组单元即可。
但是,如果我们把数据范围改成1<=L<=1000000和1<=M<=10000呢?
依然是上一道题的思想,按照读入的顺序依次覆盖一个数组。当L和M很大时,O(N*M)的算法显然不行。
现在我们换一种思路。这道题的特点是,道路的总长L很大,但是区间的数目M却相对来说小得多。那么为什么不对M个区间进行操作呢?
我们用数组x和y记录读入的点的左右顶点,然后按照x排序(按照y也可以,之后枚举的顺序要改变)。用变量head记录当前操作区间的左端点,tail记录当前操作区间的右端点。将head的值初始化为x[1],tail的值初始化为y[1]。
从2到m枚举每个区间。如果x[i]<tail且y[i]>tail这时两个区间就有交集。所以更新tail为y[i],也就是将两个区间合并成一个更大的区间,并用这个区间进行操作。(如图一)
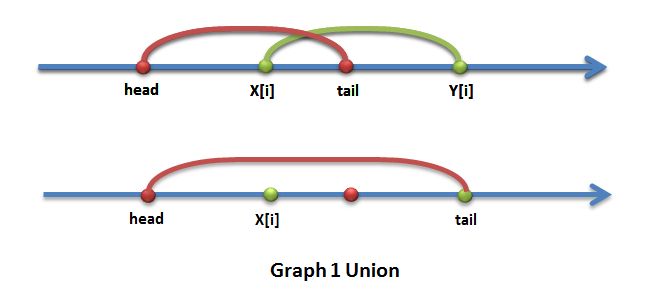
如果x[i]>tail,这时我们就要将操作区间进行更新,将head赋为x[i],将tail赋值为y[i],并将上一区间的长度累加。这样我们就可以在O(M)的时间内出解。
参考代码:
program tree;
var
l,r:array[0..10010]of longint;
x,y:array[0..10010]of longint;
i,j,k:longint;
n,m,tail,sum:longint;
f:boolean;
procedure sort(l,r:longint);
var
i,j,xx,yy: longint;
begin
i:=l;
j:=r;
xx:=x[(l+r) div 2];
repeat
while x[i]<xx do
inc(i);
while xx<x[j] do
dec(j);
if not(i>j) then
begin
yy:=x[i];
x[i]:=x[j];
x[j]:=yy;
yy:=y[i];
y[i]:=y[j];
y[j]:=yy;
inc(i);
j:=j-1;
end;
until i>j;
if l<j then
sort(l,j);
if i<r then
sort(i,r);
end;
begin
readln(n,m);
for i:=1 to m do
readln(x[i],y[i]);
sort(1,m);
f:=false;
k:=1;
tail:=y[1];
l[1]:=x[1];
for i:=1 to m do
begin
if f then
begin
r[k]:=tail;
inc(k);
l[k]:=x[i];
f:=false;
tail:=y[i];
end;
if x[i+1]>tail then f:=true //更新区间
else if y[i+1]>tail then tail:=y[i+1]; //合并区间
end;
r[k]:=tail;
for i:=1 to k do
sum:=sum+r[i]-l[i]+1;
sum:=n-sum+1;
writeln(sum);
end.
看完这道题,你是否对离散化区间有了一个初步的理解呢?简单的说,就是将对整个所给数据范围的操作转移到逐个区间的操作,从而大幅度提高算法效率。
例题2
【题目描述】(改编自BYVoid的WOW模拟赛Stage.
3
,链接文末有附)
给定n个区间,对它们着以不同的颜色。后着色的区间会覆盖该区间原来的颜色,着色按读入
顺序的
先后进行。问当着色完毕后整个区段内有多少种不同的颜色。
【输入格式】
第 1行:一个整数N,表示着色的区间数。
第
2
行至第 N+
1
行:第 i
+
1
行给出了第 i 个区间的头尾坐标 Ai,Bi。
【输出格式】
一个整数,表示区段内不同的颜色的数目。
【样例输入】
4
0
5
3
8
5
6
4
7
【样例输出】
3
【样例说明】
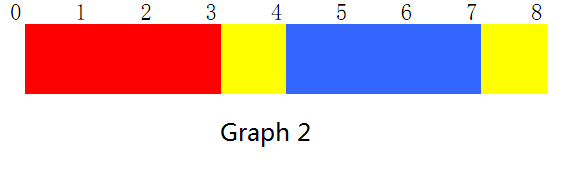
可以看到的不同颜色为3,3号区间被4号区间所覆盖。
【数据范围】
50
%
的数据满足N
<=
1
,
000
;
0
<=
Ai
<
Bi
<=
100
,
000
(
1
<=
i
<=
N);
100
%
的数据满足N
<=
20
,
000
;
0
<=
Ai
<
Bi
<=
1
,
000
,
000
,
000
(
1
<=
i
<=
N)。
数据巨大无比…如果用强大的模拟方法就是10秒也出不了解。这时我们又想到对区间进行操作。
这时区间与区间只有三种关系,相交、相离和包含。我们从后向前扫描区间,每扫到一个区间i我们就试着用它后面的区间i+1覆盖它,如果相离则再枚举i+2,一直到n。如果区间i+k有一个点在区间i中(这时包括相交和包含两种状态),则在区间i的点和它在区间i+k的对应点(i的左节点和i+k的左节点,i右节点的和i+k的右节点)所围成的区间内尝试下一个区间i+k+1,看是否能把这段区间覆盖。如此枚举到n,如果区间i还有某一部分没有被覆盖,则将记录的颜色数加1。这样我们就可以在O(kn2)的时间内出解,k是一个比较小的常数。这时我们的程序已经比原先的算法快许多了。
参考代码:
program punch;
var
x,y:array[1..20001]of longint;
v:array[0..20001]of boolean;
n,ans:longint;
i,j:longint;
procedure plus(a,b,p:longint);
begin
if v[i] then exit;
while(p<=n)and((b<=x[p])or(a>=y[p]))do inc(p);
if p>n then
begin
inc(ans);
v[i]:=true; //记录这种颜色已经加过,不能重复加。
end;
if(x[p]<b)and(x[p]>a)then plus(a,x[p],p+1); //相对的左节点构成的区间
if(y[p]<b)and(y[p]>a)then plus(y[p],b,p+1); //相对的右节点构成的区间
end;
begin
readln(n);
ans:=0;
for i:=1 to n do
readln(x[i],y[i]);
for i:=n-1 downto 1 do
plus(x[i],y[i],i+1);
writeln(ans+1);
end.
这两道题算是很有代表性的了~现在我们对区间问题的离散化处理方法有了一个大体的了解。这类题目一般是区间的范围很大,但是区间数相对来说较小。通常的思路就是找到区间之间的关系,然后逐个区间枚举,寻找满足条件的情况。因此,对区间之间关系的分析至关重要。这种敏感还要在更多的练习题中培养。
发完才发现图一的数轴不一样粗....由于改图比较麻烦,saltless就偷一下懒了~请大家谅解~>.<||
例题2题目出处:http://www.byvoid.com
本文地址:http://www.cnblogs.com/saltless/archive/2010/11/14/1877171.html
(saltless原创,转载请注明出处)