28.顺序表练习题目（2）（2023王道数据结构2.2.3节9-14题）
试题9：
线性表（a1,a2...an）的元素递增有序的储存在计算机内，要求设计一个算法：完成用最少时间在表中查找数值为x的元素，若找到，则将其与后继元素位置相交换；若找不到则将其插入表中并使其表中仍然递增有序。
注意：如果折半查找找不到的话，最后退出while循环的时候，low指针指向的是高于x的第一个元素，high指针指向的是低于x的最后一个元素。如下：
#include
#include
using namespace std;
#define MaxSize 10
#define ElemType int
//顺序表的建立
typedef struct{
int data[MaxSize]; //存储空间的基地址
int length; //当前长度
}SqList;
//顺序表的初始化
void InitList(SqList &L){
L.length = 0;
cout<<"顺序表初始化完成"<>L.data[i];
L.length++;
}
}
//打印顺序表
int Print(SqList L){
cout<<"目前顺序表为："< high;i--){ //当i=high时退出循环
L.data[i + 1] = L.data[i];
}
L.data[i + 1] = x; //将x插入high指针后一个位置
}
return L;
}
int main(){
int n,x;
cout<<"请输入顺序表L长度"<>n; //输入数组的长度n
SqList L;
InitList(L); //顺序表的初始化
CreatList(L,n); //顺序表传值
Print(L); //打印顺序表
cout<<"请输入插入或交换的元素x"<>x; //输入元素x
Print(SearchExchangeInsert(L,x)); //打印输出交换之后的顺序表
return 0;
} 输出：
请输入顺序表L长度
5
顺序表初始化完成
请传入数值
1 3 5 7 9
目前顺序表为：
1 3 5 7 9
请输入插入或交换的元素x
4
目前顺序表为：
1 3 4 5 7 9
请输入顺序表L长度
5
顺序表初始化完成
请传入数值
1 3 5 7 9
目前顺序表为：
1 3 5 7 9
请输入插入或交换的元素x
5
目前顺序表为：
1 3 7 5 9试题10：（2010年联考真题）此题和题8几乎完全一样，不多解释。
试题11：（2011年联考真题）
一个长度为L (L>=1)的升序序列S，处在第
个位置的数称为S的中位数。例如，若序列S1=(11, 13, 15, 17, 19)，则S1的中位数是15，两个序列的中位数是含它们所有元素的升序序列的中位数。例如，若S2= (2, 4，6，8, 20)，则S1和S2的中位数是11。现在有两个等长升序序列A和B，试设计一个在时间和空间两方面都尽可能高效的算法，找出两个序列A和B的中位数。要求：
（1）给出算法的基本设计思想。
（2）根据设计思想，釆用C或C++或Java语言描述算法，关键之处给出注释。
（3）说明你所设计算法的时间复杂度和空间复杂度。
我的解答：使用试题7的方法暴力求解：
//前面同之前，省略
ElemType Get2listsofmiddle(SqList L1,SqList L2){
//此函数用来查找两个等长升序序列L1，L2的中位数
int i = 0, j = 0, k = 0;
SqList L;
L.length = L1.length;
while (k < L1.length)
{
if(L1.data[i] <= L2.data[j]){
L.data[k] = L1.data[i];
k = k + 1;
i = i + 1;
}
else{
L.data[k] = L2.data[j];
k = k + 1;
j = j + 1;
}
}
return L.data[k-1];
}
int main(){
int n,x;
cout<<"请输入升序顺序表L1,L2的长度"<>n; //输入数组的长度n
SqList L1;
InitList(L1); //顺序表的初始化
CreatList(L1,n); //顺序表传值
Print(L1); //打印顺序表L1
SqList L2;
InitList(L2); //顺序表的初始化
CreatList(L2,n); //顺序表传值
Print(L2); //打印顺序表L2
x = Get2listsofmiddle(L1, L2);
cout << x << endl;
return 0;
} 输出：
请输入升序顺序表L1,L2的长度
5
顺序表初始化完成
请传入数值
11 13 15 17 19
目前顺序表为：
11 13 15 17 19
顺序表初始化完成
请传入数值
2 4 6 8 20
目前顺序表为：
2 4 6 8 20
11这种解法显然不是最优的，答案的解法：
- 若a = b，则a或b即为所求中位数，算法结束。
- 若a < b，则舍弃序列A中较小的一半，同时舍弃序列B中较大的一半，要求两次舍弃的长度相等。
- 若a > b，则舍弃序列A中较大的一半，同时舍弃序列B中较小的一半，要求两次舍弃的长度相等。
这里需要说明几点：对于一个有序线性表，去掉最高和最低的元素之后（头尾），序列的中位数不会发生变化；推广之，去掉等量的最高和最低的元素之后，序列的中位数不会发生变化。此外，两个等长度L的线性表，它们合并成有序表的长度一定是偶数。处在第个位置的数是中位数，也就是合并成有序表之后的第L个元素就是中位数。
#include
#include
using namespace std;
#define MaxSize 10
#define ElemType int
//顺序表的建立
typedef struct{
int data[MaxSize]; //存储空间的基地址
int length; //当前长度
}SqList;
//顺序表的初始化
void InitList(SqList &L){
L.length = 0;
cout<<"顺序表初始化完成"<>L.data[i];
L.length++;
}
}
//打印顺序表
int Print(SqList L){
cout<<"目前顺序表为："<>n; //输入数组的长度n
SqList L1;
InitList(L1); //顺序表的初始化
CreatList(L1,n); //顺序表传值
Print(L1); //打印顺序表L1
SqList L2;
InitList(L2); //顺序表的初始化
CreatList(L2,n); //顺序表传值
Print(L2); //打印顺序表L2
cout << Get2listsofmiddle(L1, L2) << endl;
return 0;
} 输出：
请输入升序顺序表L1,L2的长度
5
顺序表初始化完成
请传入数值
11 13 15 17 19
目前顺序表为：
11 13 15 17 19
顺序表初始化完成
请传入数值
2 4 6 8 20
目前顺序表为：
2 4 6 8 20
11特别注意：偶数部分不能写成：
else if(L1.data[m1] < L2.data[m2]){ //情况2
if((s1 + d1) % 2 == 0){ //原表长是奇数，直接取中间
s1 = m1;
d2 = m2;
}
else{ //原表长是偶数
s1 = m1;
d2 = m2 + 1;
} 否则会陷入死循环。读者可以拿d-s=1（也就是表中只剩两个元素）的情况检验一下。
试题12（2013年联考真题）：
暴力解：注意到
，构造辅助数组存放0到n-1的个数。
int GetmainElem(SqList L){
//此函数用来寻找主元素，若找不到，返回-1
SqList L0; //L0辅助数组
L0.length = L.length;
for (int i = 0; i < L0.length; i++){ //L0的所有元素置零
L0.data[i] = 0;
}
for (int i = 0; i < L.length; i++){ //统计里面的元素个数
L0.data[L.data[i]]++;
}
for (int i = 0; i < L.length; i++){ //看里面有无大于L.length/2个数的元素
if (L0.data[i]>L.length/2){
return i;
}
}
return -1;
}
int main(){
int n;
cout<<"请输入顺序表L的长度"<>n; //输入数组的长度n
SqList L;
InitList(L); //顺序表的初始化
CreatList(L,n); //顺序表传值
cout << GetmainElem(L) << endl;
return 0;
} 优解：扫描法。两两相互抵消。如果数组中存在大于一半的相同元素，首先假设第一个元素为主元素的候选元素【统计个数为1】，如果目前元素统计的个数大于0，遇到相同的数字——个数加1，不同的数字——个数减1；当元素统计的个数为0时，将遇到的数字变更为候选的主元素。循环结束时。c可能是主元素，也可能不是。遍历整个数组来统计候选主元素在数组中的个数，如果大于n/2，则存在主元素，反之则不存在。
#include
#include
using namespace std;
#define MaxSize 10
#define ElemType int
//顺序表的建立
typedef struct{
int data[MaxSize]; //存储空间的基地址
int length; //当前长度
}SqList;
//顺序表的初始化
void InitList(SqList &L){
L.length = 0;
cout<<"顺序表初始化完成"<>L.data[i];
L.length++;
}
}
//打印顺序表
int Print(SqList L){
cout<<"目前顺序表为："<L.length/2)
return c;
else
return -1;
}
int main(){
int n;
cout<<"请输入顺序表L的长度"<>n; //输入数组的长度n
SqList L;
InitList(L); //顺序表的初始化
CreatList(L,n); //顺序表传值
cout << GetmainElem(L) << endl;
return 0;
} 输出：
请输入顺序表L的长度
8
顺序表初始化完成
请传入数值
0 5 5 3 5 7 5 5
5
请输入顺序表L的长度
8
顺序表初始化完成
请传入数值
0 5 5 3 5 1 5 7
-1试题13（2018年联考真题）：
暴力求解法：这个数肯定不会超过L.length+1，所以从1开始暴力搜索。当搜索完全表都没找到整数则返回。
//前面的依旧省略
int Getlistofsmall(SqList L){
//此函数用来查找未出现的最小正整数，该正整数不会超过L.length+1
for (int i = 1; i <= L.length; i++)
{
int j = 0;
while(L.data[j] != i && j < L.length){
j++;
}
if(j == L.length)
return i;
}
return L.length + 1;
}
int main(){
int n;
cout<<"请输入顺序表L的长度"<>n; //输入数组的长度n
SqList L;
InitList(L); //顺序表的初始化
CreatList(L,n); //顺序表传值
cout << Getlistofsmall(L) << endl;
return 0;
} 时间复杂度最低的解法：用空间换时间，构造辅助数组解决。
#include
#include
using namespace std;
#define MaxSize 10
#define ElemType int
//顺序表的建立
typedef struct{
int data[MaxSize]; //存储空间的基地址
int length; //当前长度
}SqList;
//顺序表的初始化
void InitList(SqList &L){
L.length = 0;
cout<<"顺序表初始化完成"<>L.data[i];
L.length++;
}
}
//打印顺序表
int Print(SqList L){
cout<<"目前顺序表为："< 0 && L.data[i] <= L.length){
a[L.data[i] - 1] = 1;
}
}
for (int i = 0; i < L.length; i++){
if (a[i] == 0){
return i + 1;
}
}
return L.length + 1;
}
int main(){
int n;
cout<<"请输入顺序表L的长度"<>n; //输入数组的长度n
SqList L;
InitList(L); //顺序表的初始化
CreatList(L,n); //顺序表传值
cout << Getlistofsmall(L) << endl;
return 0;
} 输出：
请输入顺序表L的长度
4
顺序表初始化完成
请传入数值
-5 3 2 3
1
请输入顺序表L的长度
3
顺序表初始化完成
请传入数值
1 2 3
4试题14（2020年联考真题）：
暴力求解：
int abs(int a){
if(a>=0)
return a;
else
return -a;
}
int GetDmin(SqList L1,SqList L2,SqList L3){
//此函数用来求解三元组最小距离D=|a-b|+|b-c|+|c-a|.
int D_Min = 10000;
int m, n, t; //记录最小值对应的元素
for (int i = 0; i < L1.length;i++){
for (int j = 0; j < L2.length;j++){
for (int k = 0; k < L3.length;k++){
int D = abs(L1.data[i] - L2.data[j]) + abs(L2.data[j] - L3.data[k]) + abs(L3.data[k] - L1.data[i]);
if(D>n1; //输入数组的长度n1
SqList L1;
InitList(L1); //顺序表的初始化
CreatList(L1,n1); //顺序表传值
cout<<"请输入顺序表L2的长度"<>n2; //输入数组的长度n1
SqList L2;
InitList(L2); //顺序表的初始化
CreatList(L2,n2); //顺序表传值
cout<<"请输入顺序表L3的长度"<>n3; //输入数组的长度n1
SqList L3;
InitList(L3); //顺序表的初始化
CreatList(L3,n3); //顺序表传值
cout<<"最小距离D_Min是"< 输出：
请输入顺序表L1的长度
3
顺序表初始化完成
请传入数值
-1 0 9
请输入顺序表L2的长度
4
顺序表初始化完成
请传入数值
-25 -10 10 11
请输入顺序表L3的长度
5
顺序表初始化完成
请传入数值
2 9 17 30 41
最小距离D_Min是
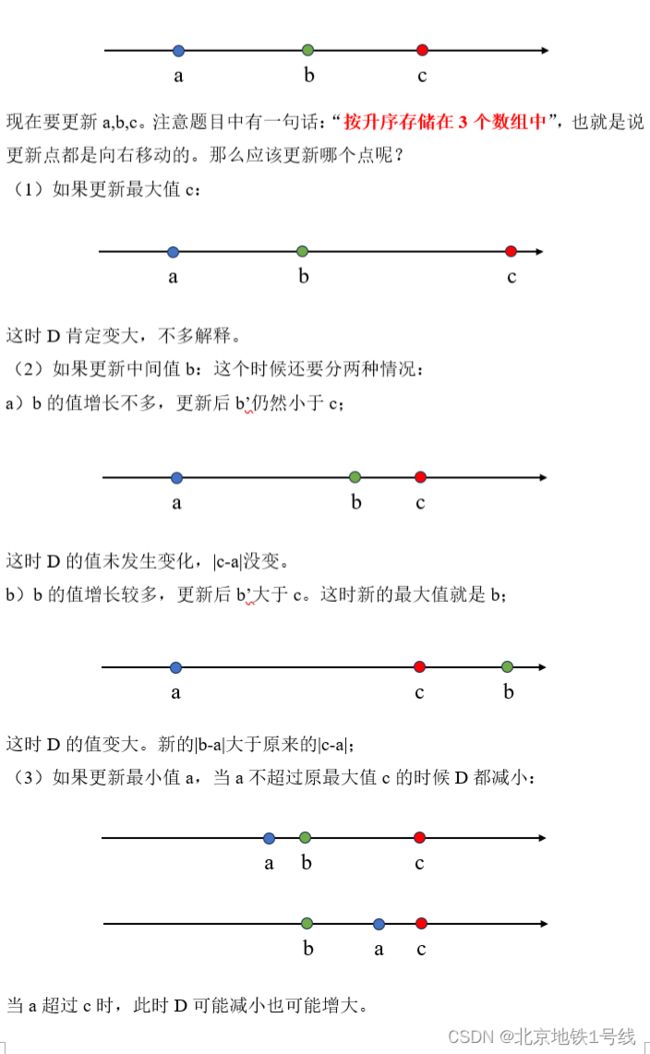
2最优解法：实际上D就是2倍的最大值减去最小值。每次只更新最小值可以回避掉大量的试错成本：
#include
#include
using namespace std;
#define MaxSize 10
#define ElemType int
//顺序表的建立
typedef struct{
int data[MaxSize]; //存储空间的基地址
int length; //当前长度
}SqList;
//顺序表的初始化
void InitList(SqList &L){
L.length = 0;
cout<<"顺序表初始化完成"<>L.data[i];
L.length++;
}
}
//打印顺序表
int Print(SqList L){
cout<<"目前顺序表为："<=0)
return a;
else
return -a;
}
bool ifamin(int a,int b,int c){ //判断第一个元素是不是三元组的最小值
if(a <= b && a <= c){
return true;
}
else{
return false;
}
}
int GetDmin(SqList L1,SqList L2,SqList L3){
//此函数用来求解三元组最小距离D=|a-b|+|b-c|+|c-a|.
int D_Min = 10000;
int i = 0, j = 0, k = 0;
int m, n, t; //记录最小值对应的元素
while (i>n1; //输入数组的长度n1
SqList L1;
InitList(L1); //顺序表的初始化
CreatList(L1,n1); //顺序表传值
cout<<"请输入顺序表L2的长度"<>n2; //输入数组的长度n1
SqList L2;
InitList(L2); //顺序表的初始化
CreatList(L2,n2); //顺序表传值
cout<<"请输入顺序表L3的长度"<>n3; //输入数组的长度n1
SqList L3;
InitList(L3); //顺序表的初始化
CreatList(L3,n3); //顺序表传值
cout<<"最小距离D_Min是"<