AVL树详解
一、简介
AVL树是根据它的发明者G.M. Adelson-Velsky和E.M. Landis命名的。它是最先发明的自平衡二叉查找树,也被称为高度平衡树。
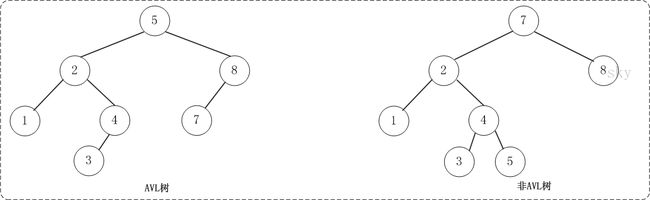
上面的两张图片,左边的是AVL树,它的任何节点的两个子树的高度差别都<=1;而右边的不是AVL树,因为7的两颗子树的高度相差为2(以2为根节点的树的高度是3,而以8为根节点的树的高度是1)。
AVL树的查找、插入和删除在平均和最坏情况下都是O(logn)。
如果在AVL树中插入或删除节点后,使得高度之差大于1。此时,AVL树的平衡状态就被破坏,它就不再是一棵二叉树;为了让它重新维持在一个平衡状态,就需要对其进行旋转处理。学AVL树,重点的地方也就是它的旋转算法;
二、旋转算法
在所有的不平衡情况中,都是按照先寻找最小不平衡树,然后寻找所属的不平衡类别,再根据 4 种类别进行固定化程序的操作。
注意在寻找最小不平衡子树的时候,这个平衡因子的定义:
它的任何节点的两个子树的高度差别都<=1。
我之前有个误区:
我之前认为这个不是平衡二叉树,所以自己做了RL旋转,发现还是不平衡
后来发现这个是一个平衡二叉树,平衡二叉树的定义是它的任何节点的两个子树的高度差别都<=1。这里重点理解子树的高度,子树的高度是子树的最深高度,100的左子树的高度是3而不是2
1.不平衡的四种类别
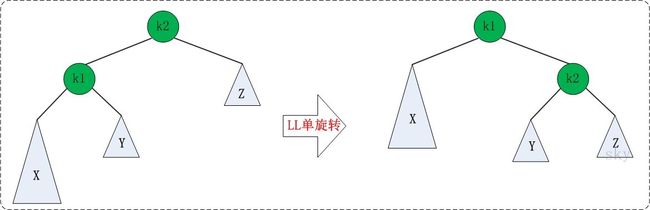
(1).LL单旋
(2).RR单旋
(3).LR双旋
(4).RL 双旋
为什么可以归纳成4种而且只有四种?
因为是最小不平衡子树、又是二叉树。所以是2的2次幂 前面那个2为底是二叉树定的,后面那个2次幂是最小不平衡子树保证的不会是3次幂或者更大
2.如何查找最小不平衡子树和如何判断是属于哪种情况旋转
(1).查找最小不平衡子树
递归查找,计算平衡因子,找到最后的节点就是最小不平衡子树的根节点
(2).判断是属于哪种旋转情况
先找到高度高的子树是哪一边,然后再判断子树的哪边高,可以归纳为
1).最小不平衡子树的左子树比右子树更高,最小不平衡子树的左子树的左子树比最小不平衡子树的左子树的右子树更高,这种就是LL旋转
2).最小不平衡子树的右子树比左子树更高,最小不平衡子树的右子树的右子树比最小不平衡子树的右子树的左子树更高,这种就是RR旋转
3).最小不平衡子树的左子树比右子树更高,最小不平衡子树的左子树的右子树比最小不平衡子树的左子树的左子树更高,这种就是LR
4).最小不平衡子树的右子树比左子树更高,最小不平衡子树的右子树的左子树比最小不平衡子树的右子树的右子树更高,这种就是RL
发现规律没有,就是两次比较哪边更高这个缩写就是哪个,LL都是左边高然后左边的左边高,LR是左边高然后左边的右边高,RR是右边高然后右边的右边高,RL是右边高右边的左边高
3.代码实现
(1).插入
/*
* 将结点插入到AVL树中,并返回根节点
*
* 参数说明:
* tree AVL树的根结点
* key 插入的结点的键值
* 返回值:
* 根节点
*/
private AVLTreeNode insert(AVLTreeNode tree, T key) {
if (tree == null) {
// 新建节点 递归的出口
tree = new AVLTreeNode(key, null, null);
} else {
//比较根结点和插入节点的大小
int cmp = key.compareTo(tree.key);
if (cmp < 0) { // 应该将key插入到"tree的左子树"的情况
//递归调用寻找应该插入的位置
tree.left = insert(tree.left, key);
//插入节点后,若AVL树失去平衡,则进行相应的调节。
//如何查找的最小不平衡子树?
// 因为是递归调用,所以插入一个节点之后第一次判断成立一定是最小不平衡子树的根节点
//为什么只判断了tree.left - tree.right?
//因为通过cmp < 0这个判断成立会将key插入到trr的左子树,所以只要执行到这里左子树一定
// 比右子树高
if (height(tree.left) - height(tree.right) == 2) {
//上面判断成立说明最小不平衡子树的左子树比右子树高,所以第一个类型是L
//下面这个判断,把要插入节点的值和最小不平衡子树的左子树的值比较来确定第二个类型
//如果比最小不平衡子树的左子树的值小则是LL,否则是LR
if (key.compareTo(tree.left.key) < 0)
tree = leftLeftRotation(tree);
else
tree = leftRightRotation(tree);
}
} else if (cmp > 0) { // 应该将key插入到"tree的右子树"的情况
tree.right = insert(tree.right, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
//同理和上面分析的一样
if (height(tree.right) - height(tree.left) == 2) {
if (key.compareTo(tree.right.key) > 0)
tree = rightRightRotation(tree);
else
tree = rightLeftRotation(tree);
}
} else { // cmp==0
System.out.println("添加失败:不允许添加相同的节点!");
}
}
//因为要插入节点,所以需要维护有关的节点,又是因为递归查找正好相关节点都会走一下这个方法,所以
//可以直接在这里计算每个节点的高度
tree.height = max( height(tree.left), height(tree.right)) + 1;
return tree;
} 主要是利用递归的特性找到最小不平衡子树。
(2).删除
先科普一下:
二叉搜索树的前驱和后继节点
查找前驱节点规则
若一个节点有左子树,那么该节点的前驱节点是其左子树中val值最大的节点
若一个节点没有左子树,那么判断该节点和其父节点的关系
2.1 若该节点是其父节点的右边孩子,那么该节点的前驱结点即为其父节点。
2.2 若该节点是其父节点的左边孩子,那么需要沿着其父亲节点一直向树的顶端寻找,直到找到一个节点P,P节点是其父节点Q的右边孩子,那么Q就是该节点的后继节点
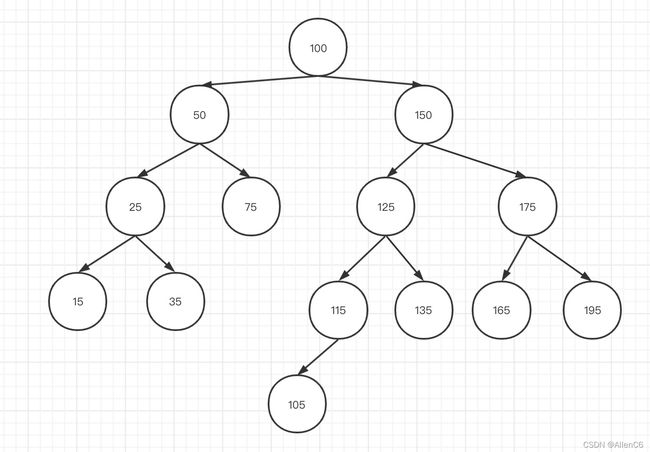
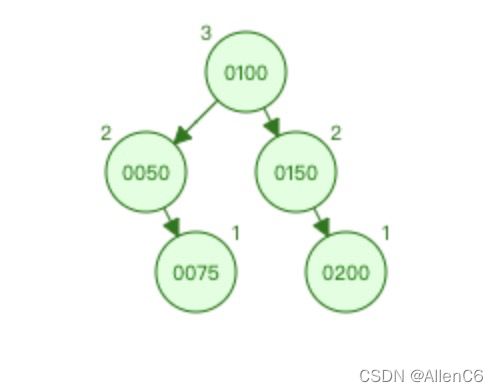
这个2.2不好理解看个图:
30没有前驱,125的前驱是100,按照2.2的理解150是P节点,Q节点是100
查找后继节点规则
若一个节点有右子树,那么该节点的后继节点是其右子树中val值最小的节点
若一个节点没有右子树,那么判断该节点和其父节点的关系
2.1 若该节点是其父节点的左边孩子,那么该节点的后继结点即为其父节点
2.2 若该节点是其父节点的右边孩子,那么需要沿着其父亲节点一直向树的顶端寻找,直到找到一个节点P,P节点是其父节点Q的左边孩子,那么Q就是该节点的后继节点
同样2.2看图说话:
75节点的后继是100,P是50,Q是100
200没有后继节点
删除的思路
(1).删除的是叶子结点,直接删除,删除完了需要看是不是影响平衡了
(2).删除的节点只有一个孩子即只有左孩子或者右孩子,直接用这个孩子代替这个节点,删除完了也需要判断是不是影响平衡了
(3).删除的节点有两个孩子,如果左子树比右子树高则把当前节点的前驱节点的值复制过来,然后删除前驱节点,这样破坏树的平衡的可能性就会变小,因为删除的是高度高的子树
如果右子树比左子树高则把当前节点的后继节点的值复制过来,然后删除后继节点,这样破坏树的平衡的可能性就会变小,原因和上面一样。
如果左右子树高度相等,用这个节点的前驱或者后继代替删除都行。
/*
* 删除结点(z),返回根节点
*
* 参数说明:
* tree AVL树的根结点
* z 待删除的结点
* 返回值:
* 根节点
*/
private AVLTreeNode remove(AVLTreeNode tree, AVLTreeNode z) {
// 根为空 或者 没有要删除的节点,直接返回null。
if (tree==null || z==null)
return null;
int cmp = z.key.compareTo(tree.key);
if (cmp < 0) { // 待删除的节点在"tree的左子树"中
tree.left = remove(tree.left, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.right) - height(tree.left) == 2) {
AVLTreeNode r = tree.right;
if (height(r.left) > height(r.right))
tree = rightLeftRotation(tree);
else
tree = rightRightRotation(tree);
}
} else if (cmp > 0) { // 待删除的节点在"tree的右子树"中
tree.right = remove(tree.right, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.left) - height(tree.right) == 2) {
AVLTreeNode l = tree.left;
if (height(l.right) > height(l.left))
tree = leftRightRotation(tree);
else
tree = leftLeftRotation(tree);
}
} else { // tree是对应要删除的节点。
// tree的左右孩子都非空
if ((tree.left!=null) && (tree.right!=null)) {
if (height(tree.left) > height(tree.right)) {
// 如果tree的左子树比右子树高;
// 则(01)找出tree的左子树中的最大节点
// (02)将该最大节点的值赋值给tree。
// (03)删除该最大节点。
// 这类似于用"tree的左子树中最大节点"做"tree"的替身;
// 这个在纸上画一下就能体会到这么做的好处
// 采用这种方式的好处是:删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。?
// 感觉应该是树仍是有序的,有可能不平衡,不平衡再调整
AVLTreeNode max = maximum(tree.left);
tree.key = max.key;
tree.left = remove(tree.left, max);
} else {
// 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1)
// 则(01)找出tree的右子树中的最小节点
// (02)将该最小节点的值赋值给tree。
// (03)删除该最小节点。
// 这类似于用"tree的右子树中最小节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。?
// 感觉应该是树仍是有序的,有可能不平衡,不平衡再调整
AVLTreeNode min = maximum(tree.right);
tree.key = min.key;
tree.right = remove(tree.right, min);
}
} else {
AVLTreeNode tmp = tree;
//这个写的挺巧妙的,进到else里面可能是
// tree.left是null 或者 tree.right是null 或者 两个都是null
//下面这个写法如果 tree.left!=null说明 tree.right是null
//如果tree.left 是 null 不管 tree.right是不是null都返回tree.right
tree = (tree.left!=null) ? tree.left : tree.right;
tmp = null;
}
}
return tree;
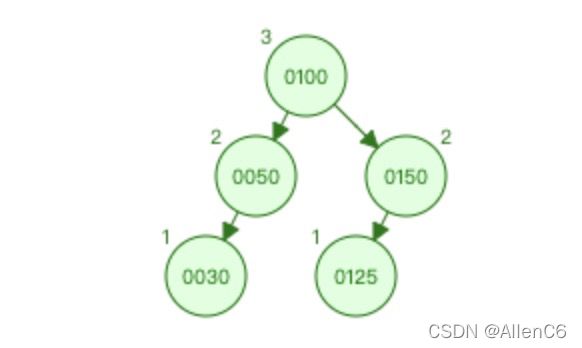
} 注意AVL的插入操作仅对第一个不平衡结点的子树进行平衡操作,而AVL的删除需要不断地回溯,直到根结点平衡为止 如图:
删除80节点就需要不断回溯,在上面的代码中回溯是借助递归的特性实现的。
(3).总体实现
public class AVLTree> {
private AVLTreeNode mRoot; // 根结点
// AVL树的节点(内部类)
class AVLTreeNode> { //泛型决定了key的类型是实现了Comparable可以直接调用compareTo方法进行比较
T key; // 关键字(键值)
int height; // 高度
AVLTreeNode left; // 左孩子
AVLTreeNode right; // 右孩子
public AVLTreeNode(T key, AVLTreeNode left, AVLTreeNode right) {
this.key = key;
this.left = left;
this.right = right;
this.height = 0;
}
}
// 构造函数
public AVLTree() {
mRoot = null;
}
/*
* 获取树的高度
*/
private int height(AVLTreeNode tree) {
if (tree != null)
return tree.height;
return 0;
}
public int height() {
return height(mRoot);
}
/*
* 比较两个值的大小
*/
private int max(int a, int b) {
return Math.max(a, b);
}
/*
* 前序遍历"AVL树"
*/
private void preOrder(AVLTreeNode tree) {
if(tree != null) {
System.out.print(tree.key+" "); //递归实现的前中后遍历全看这一句的顺序
preOrder(tree.left);
preOrder(tree.right);
}
}
public void preOrder() {
preOrder(mRoot);
}
/*
* 中序遍历"AVL树"
*/
private void inOrder(AVLTreeNode tree) {
if(tree != null)
{
inOrder(tree.left);
System.out.print(tree.key+" ");
inOrder(tree.right);
}
}
/**
* 中序遍历 非递归 自己写的
* 不用递归就只能用循环了,不用递归我们就得记录,思考一下用栈来记录最合适
* 首先从根结点开始入栈,不断遍历左孩子并且压入栈中,直到没有左孩子,
* 并且把栈顶的节点弹出,并且打印输出(这个好好理解,这个栈记录的左孩子就是为了查它有没有右子树的,
* 只要做了这一操作它就没有作用了可以弹出,右子树搞完了就再弹下一个记录的节点),
* 并且需要判断这个节点有没有右孩子,如果有又得不断遍历这个右孩子的左孩子并且压栈记录下来(重复从根节点开始的操作)
*
* @param
*/
public void midOrder() {
AVLTreeNode Node = mRoot;
if (Node == null) {
System.out.println("null");
return;
}
Stack> stack = new Stack<>();
stack.push(Node);
while (!stack.isEmpty()) {
//为了满足循环条件不得不先把根结点添加进去,先把根结点添加进去就会导致在循环中必须直接添加下一个节点
//,直接添加下一个节点这个也就造成了(当前节点不会被压栈记录),如果出现拐点,if(Node != null)成立在
//就是右孩子节点,第一个右孩子不会被加入,所以要单独写一个push(这个拐点在逻辑上可以理解为又一个根结点)
//或者你选则改变循环条件,把根结点也带入循环(下面有改进之后的changeMidOrder方法)
if (Node != null) {
Node = Node.left;//这里为了迁就先把根结点加入到栈中,直接添加下一个节点
if (Node != null){
stack.push(Node);
}
} else {
Node = stack.pop();
System.out.print(Node.key+" ");
Node = Node.right;
//这里就是单独写的push 不单独写,这个第一个右孩子会丢失
if (Node != null){
stack.push(Node);
}
}
}
}
//网上查到的非递归中序遍历
public void netMidOrder() {
AVLTreeNode Node = mRoot;
if (Node == null) {
System.out.println("null");
return;
}
Stack> stack = new Stack<>();
while (Node != null || !stack.empty()) {
while (Node != null) {
stack.push(Node);
Node = Node.left;
}
if (!stack.empty()) {
Node = stack.pop();
System.out.printf(Node.key + " ");
Node = Node.right;
}
}
}
//看了网上的非递归中序遍历后,改进自己的
public void changeMidOrder() {
AVLTreeNode Node = mRoot;
if (Node == null) {
System.out.println("null");
return;
}
Stack> stack = new Stack<>();
while (Node != null || !stack.isEmpty()) {
if (Node != null) {
stack.push(Node);
Node = Node.left;
} else {
Node = stack.pop();
System.out.print(Node.key+" ");
Node = Node.right;
}
}
}
public void inOrder() {
inOrder(mRoot);
}
/*
* 后序遍历"AVL树"
*/
private void postOrder(AVLTreeNode tree) {
if(tree != null) {
postOrder(tree.left);
postOrder(tree.right);
System.out.print(tree.key+" ");
}
}
public void postOrder() {
postOrder(mRoot);
}
/*
* (递归实现)查找"AVL树x"中键值为key的节点
*/
private AVLTreeNode search(AVLTreeNode x, T key) {
if (x==null)
return x;
int cmp = key.compareTo(x.key);
if (cmp < 0)
return search(x.left, key);
else if (cmp > 0)
return search(x.right, key);
else
return x;
}
public AVLTreeNode search(T key) {
return search(mRoot, key);
}
/*
* (非递归实现)查找"AVL树x"中键值为key的节点
* 不是递归就是循环
*/
private AVLTreeNode iterativeSearch(AVLTreeNode x, T key) {
while (x!=null) {
int cmp = key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else
return x;
}
return x;
}
public AVLTreeNode iterativeSearch(T key) {
return iterativeSearch(mRoot, key);
}
/*
* 查找最小结点:返回tree为根结点的AVL树的最小结点。
*/
private AVLTreeNode minimum(AVLTreeNode tree) {
if (tree == null)
return null;
while(tree.left != null)
tree = tree.left;
return tree;
}
public T minimum() {
AVLTreeNode p = minimum(mRoot);
if (p != null)
return p.key;
return null;
}
/*
* 查找最大结点:返回tree为根结点的AVL树的最大结点。
*/
private AVLTreeNode maximum(AVLTreeNode tree) {
if (tree == null)
return null;
while(tree.right != null)
tree = tree.right;
return tree;
}
public T maximum() {
AVLTreeNode p = maximum(mRoot);
if (p != null)
return p.key;
return null;
}
/*
* LL:左左对应的情况(左单旋转)。
*
* 返回值:旋转后的根节点
*/
private AVLTreeNode leftLeftRotation(AVLTreeNode k2) {
AVLTreeNode k1;
k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
//在旋转过程中没有做影响k2.left和k2.right高度的操作所以可以直接使用
k2.height = max( height(k2.left), height(k2.right)) + 1;
//旋转后 k1.left的高度也不会变,因为LL类型k1.left的高度是由k1.left的left决定的
k1.height = max( height(k1.left), k2.height) + 1;
return k1;
}
/*
* RR:右右对应的情况(右单旋转)。
*
* 返回值:旋转后的根节点
*/
private AVLTreeNode rightRightRotation(AVLTreeNode k1) {
AVLTreeNode k2;
k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k1.height = max( height(k1.left), height(k1.right)) + 1;
k2.height = max( height(k2.right), k1.height) + 1;
return k2;
}
/*
* LR:左右对应的情况(左双旋转)。
*
* 返回值:旋转后的根节点
*/
private AVLTreeNode leftRightRotation(AVLTreeNode k3) {
k3.left = rightRightRotation(k3.left);
return leftLeftRotation(k3);
}
/*
* RL:右左对应的情况(右双旋转)。
*
* 返回值:旋转后的根节点
*/
private AVLTreeNode rightLeftRotation(AVLTreeNode k1) {
k1.right = leftLeftRotation(k1.right);
return rightRightRotation(k1);
}
/*
* 将结点插入到AVL树中,并返回根节点
*
* 参数说明:
* tree AVL树的根结点
* key 插入的结点的键值
* 返回值:
* 根节点
*/
private AVLTreeNode insert(AVLTreeNode tree, T key) {
if (tree == null) {
// 新建节点 递归的出口
tree = new AVLTreeNode(key, null, null);
} else {
//比较根结点和插入节点的大小
int cmp = key.compareTo(tree.key);
if (cmp < 0) { // 应该将key插入到"tree的左子树"的情况
//递归调用寻找应该插入的位置
tree.left = insert(tree.left, key);
//插入节点后,若AVL树失去平衡,则进行相应的调节。
//如何查找的最小不平衡子树?
// 因为是递归调用,所以插入一个节点之后第一次判断成立一定是最小不平衡子树的根节点
//为什么只判断了tree.left - tree.right?
//因为通过cmp < 0这个判断成立会将key插入到trr的左子树,所以只要执行到这里左子树一定
// 比右子树高
if (height(tree.left) - height(tree.right) == 2) {
//上面判断成立说明最小不平衡子树的左子树比右子树高,所以第一个类型是L
//下面这个判断,把要插入节点的值和最小不平衡子树的左子树的值比较来确定第二个类型
//如果比最小不平衡子树的左子树的值小则是LL,否则是LR
if (key.compareTo(tree.left.key) < 0)
tree = leftLeftRotation(tree);
else
tree = leftRightRotation(tree);
}
} else if (cmp > 0) { // 应该将key插入到"tree的右子树"的情况
tree.right = insert(tree.right, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
//同理和上面分析的一样
if (height(tree.right) - height(tree.left) == 2) {
if (key.compareTo(tree.right.key) > 0)
tree = rightRightRotation(tree);
else
tree = rightLeftRotation(tree);
}
} else { // cmp==0
System.out.println("添加失败:不允许添加相同的节点!");
}
}
//因为要插入节点,所以需要维护有关的节点,又是因为递归查找正好相关节点都会走一下这个方法,所以
//可以直接在这里计算每个节点的高度
tree.height = max( height(tree.left), height(tree.right)) + 1;
return tree;
}
public void insert(T key) {
mRoot = insert(mRoot, key);
}
/*
* 删除结点(z),返回根节点
*
* 参数说明:
* tree AVL树的根结点
* z 待删除的结点
* 返回值:
* 根节点
*/
private AVLTreeNode remove(AVLTreeNode tree, AVLTreeNode z) {
// 根为空 或者 没有要删除的节点,直接返回null。
if (tree==null || z==null)
return null;
int cmp = z.key.compareTo(tree.key);
if (cmp < 0) { // 待删除的节点在"tree的左子树"中
tree.left = remove(tree.left, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.right) - height(tree.left) == 2) {
AVLTreeNode r = tree.right;
if (height(r.left) > height(r.right))
tree = rightLeftRotation(tree);
else
tree = rightRightRotation(tree);
}
} else if (cmp > 0) { // 待删除的节点在"tree的右子树"中
tree.right = remove(tree.right, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.left) - height(tree.right) == 2) {
AVLTreeNode l = tree.left;
if (height(l.right) > height(l.left))
tree = leftRightRotation(tree);
else
tree = leftLeftRotation(tree);
}
} else { // tree是对应要删除的节点。
// tree的左右孩子都非空
if ((tree.left!=null) && (tree.right!=null)) {
if (height(tree.left) > height(tree.right)) {
// 如果tree的左子树比右子树高;
// 则(01)找出tree的左子树中的最大节点
// (02)将该最大节点的值赋值给tree。
// (03)删除该最大节点。
// 这类似于用"tree的左子树中最大节点"做"tree"的替身;
// 这个在纸上画一下就能体会到这么做的好处
// 采用这种方式的好处是:删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。?
// 感觉应该是树仍是有序的,有可能不平衡,不平衡再调整
AVLTreeNode max = maximum(tree.left);
tree.key = max.key;
tree.left = remove(tree.left, max);
} else {
// 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1)
// 则(01)找出tree的右子树中的最小节点
// (02)将该最小节点的值赋值给tree。
// (03)删除该最小节点。
// 这类似于用"tree的右子树中最小节点"做"tree"的替身;
// 采用这种方式的好处是:删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。?
// 感觉应该是树仍是有序的,有可能不平衡,不平衡再调整
AVLTreeNode min = maximum(tree.right);
tree.key = min.key;
tree.right = remove(tree.right, min);
}
} else {
AVLTreeNode tmp = tree;
//这个写的挺巧妙的,进到else里面可能是
// tree.left是null 或者 tree.right是null 或者 两个都是null
//下面这个写法如果 tree.left!=null说明 tree.right是null
//如果tree.left 是 null 不管 tree.right是不是null都返回tree.right
tree = (tree.left!=null) ? tree.left : tree.right;
tmp = null;
}
}
return tree;
}
public void remove(T key) {
AVLTreeNode z;
if ((z = search(mRoot, key)) != null)
mRoot = remove(mRoot, z);
}
/*
* 销毁AVL树
*/
private void destroy(AVLTreeNode tree) {
if (tree==null)
return ;
if (tree.left != null)
destroy(tree.left);
if (tree.right != null)
destroy(tree.right);
tree = null;
}
public void destroy() {
destroy(mRoot);
}
/*
* 打印"二叉查找树"
*
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
private void print(AVLTreeNode tree, T key, int direction) {
if(tree != null) {
if(direction==0) // tree是根节点
System.out.printf("%2d is root\n", tree.key, key);
else // tree是分支节点
System.out.printf("%2d is %2d's %6s child\n", tree.key, key, direction==1?"right" : "left");
print(tree.left, tree.key, -1);
print(tree.right,tree.key, 1);
}
}
public void print() {
if (mRoot != null)
print(mRoot, mRoot.key, 0);
}
}