lingo解题报告内容解释

1.2菜单介绍

1.2.1 File

1 New

新建一个窗口,当你执行这个命令时,会出现如下对话框:

　

　

你可以在对话框中选择你想要建立的类型.类型如下:

1)扩展名为(*.lg4)

LG4格式是LINGO4.0的版本,是在Windows下最主要的储存文件格式,这种格式支持字体格式,自定义格式以及动态连接,  LG4以二进制格式存储,所以不能被其它的应用软件直接读取.

2)扩展名为(*.lng)

LNG是捷便的存储方式,是4.0版本前的标准文件格式,为了与前版本的兼容,所以还一直在用,LNG文件是以ASCII形式存储的,所以能被支持文本文件的应用程序读取.该格式不支持多种字体.

3)扩展名为(*.ltd)

LTD是数据文件,可以从@FILE函数导入数据,@FILE函数只能读取文本文件,所以所有的LTD文件是以ASCII形式存储,也不支持多种字体.

4)扩展名为(*.ltf)

LTF是LINGO的调试文件格式,也是以ASCII格式存储,能直接被LINGO的File|Take command执行.

2 Log Output

输出文本文件，可以将随后原输出到报告窗口的内容输出到文本中.该命令与Maple中的writeto命令非常相似.

在Maple中输入如下：

> x:=sin(5.);

writeto("c://maple.txt");

y:=x+1:

print(x,y);

print(x);

> y;

> writeto(terminal);

> y;

执行菜单中的Edit|Excute|Worksheet,按钮，窗口重新显示如下：

> x:=sin(5.);

writeto("c://maple.txt");

y:=x+1:

print(x,y);

   print(x);

             x:=-.9589242747

  

> y;

>writeto(terminal);

> y;

                           0.4010757253

　

而在C盘的maple.txt文件的内容为：

                          -.9589242747, .0410757253

 

                                -.9589242747

 

                                 .0410757253

从中可以知道，用了writeto(filename)命令以后把结果输出到filename中.直到碰到writeto(terminal)命令时，才重新在工作窗口中显示.

当你点击菜单File|LogOutput时，系统出现保存对话框，系统就会将命令窗口中的输出结果保存到指定的文件中.

3 Import LINDO File

该命令是用来导入LINDO软件保存的LINDO文件(*.LTX)格式.只要在LINGO中导入LINDO文件格式,LINGO系统自动将该文件转化为LINGO可执行语句.

1.2.2 Edit

1 Paste Function

用该命令可以在当前点插入LINGO的内部函数,

2 Select Fonts

设置字体类型,字体大小，字体颜色.

1.2.3 LINGO

1 Solve

用solve命令对当前窗口中的模型求解,该命令只对report script窗口起作用,不能对数据窗口求解.

当你对一个模型进行求解,LINGO首先检查该模型的语句格式是否正确,如果LINGO发现在语句中存在错误,将会出现类似于如下的对话框：

　

　

在上图的Error Text框中,LINGO提示发生语句错误的行数及该行的内容.在通常情况下,LINGO系统能很好的指出错误,但是有时也会提供错误的信息.

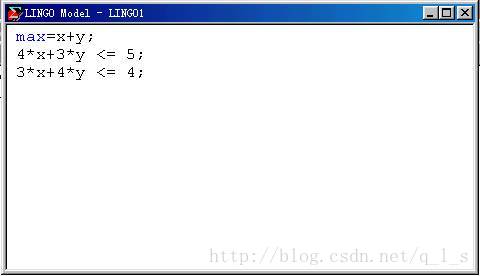
如果在编译的过程中没有语法的错误,LINGO将调用适当的内部函数对模型进行优化求解.假如我们在工作窗口输入如下内容：

　

　

点击菜单LINGO|SOLVE，或者点击工具栏，将会在屏幕上显示LINGO解的状态窗口（Solver Status Windows）：

　

　

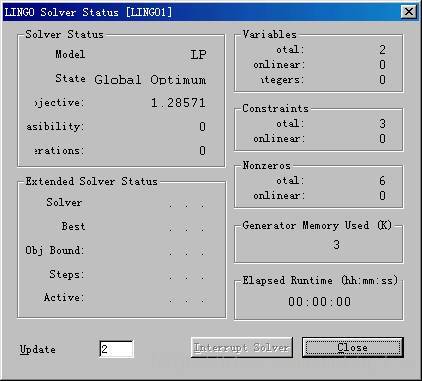
该状态窗口用于跟踪整个求解过程,下面我们将详细的描写该窗口中的一些主要的内容.

1） 按钮

在解的状态窗口提供了两个按钮,一个为关闭按钮 (Close),另一个是打断（interruptSolver）求解按钮，该按钮的作用是阻止LINGO求解下一个迭代.在线性模型中，LINGO一般能给出优化解（除整数规划时没有整数解），如果这线性模型被打断了，LINGO返回的将是无意义的,应该被忽略的值.

注意：如果你按了interruptsolver这个按钮,解的情况是这样的：

·        毫无疑问这不是最优解;

·        解可能不能全部满足约束条件;

·        如果这个是线性模型，这个解毫无意义.

2） 文本框

在该窗口中有一个文本框,该文本框的作用是更新状态窗口的相隔时间,单位为秒,在默认时为2秒.

3）状态窗口（Solver StatusBox）

状态窗口的详细的介绍如下：

 

Model Class:	模型类别显示的模型类别为LP, QP ILP, QP, ILP, IQP, LP, NLP等
State:	Possible states are "Global Optimum", "Local Optimum", "Feasible", "Infeasible", "Unbounded", "Interrupted", and "Undetermined".
Objective:	目标函数的当前值.
Infeasibility:	不满足约束条件的个数.
Iterations  :	迭代次数

　

其中

缩写	类型	描述
LP	线性模型	所有的表达式是线性，并且模型的约束条件中变量没有被约束为整数。
QP	二次模型	所有表达式是线性或二次型，没有整数约束。
ILP	整数线性模型	所有的表达式是线性，在变量中存在整数约束。
IQP	整数二次模型	所有表达式是线性或二次型,在变量中存在整数约束。
PILP	纯整数线性模型	所有表达式是线性，所有变量是整数。
PIQP	纯整数二次模型	所有表达式是线性或二次型，所有变量是整数。
NLP	非线性模型	至少存在一个非线性的表达式

 

一旦LINGO处理完成该模型,建立一个包括该模型解的报告（Solve Report）窗口.你可以通过拉窗口的滚动条,检查该窗口内部的内容.该窗口如下：

　

　

第一：Solution Report告诉我们求该模型迭带的次数是0次；第二：该目标函数的最大值是1.285714；第三：取到最优值时变量X、Y分别为1.142857、0.1428571.

我们用数学软件Maple来验证该结果：

>  with(simplex):

maximize( x+y, {4*x+3*y <= 5, 3*x+4*y <= 4 } );

> evalf(%);

 

比较LINGO与Maple所求的结果,完全一致.

在SolutionReport中还包括The Reduced Costs, Slack or Surplus, Dual Price栏.

 

Reduced Cost：

假设X的reduce cost值为10，则X系数加上10时，求优化模型变量取值不变.例如下模型：

MAX = 4.0 * TOM + 3.0 *DICK    +2.0 *HARRY;

       2.5 *TOM                 +3.1 *HARRY <= 5;

       2.0 * TOM + 0.7 *DICK    +0.4 *HARRY <= 1;

 

求解得到solution report如下：

  Global optimal solution found atiteration:            0

  Objectivevalue:                                10.57143

 

 

                      Variable          Value        Reduced Cost

                           TOM       2.000000            0.000000

                          DICK      0.8571429           0.000000

                         HARRY       0.000000           3.611429

 

                           Row    Slack or Surplus      Dual Price

                             1        10.57143           1.000000

                             2        0.000000           1.257143

                             3        0.000000           4.285714

该解中变量HARRY的Reduced Cost为3.611429，现在我们把HARRY前的系数加2，得到的新模型如下：

MAX = 4.0 * TOM + 3.0 *DICK    +4.0 *HARRY;

       2.5 *TOM                 +3.1 *HARRY <= 5;

       2.0 * TOM + 0.7 *DICK    +0.4 *HARRY <= 1;

再求解得到solution report如下：

  Global optimal solution found atiteration:            0

  Objectivevalue:                                10.57143

 

 

                      Variable          Value        Reduced Cost

                           TOM       2.000000           0.000000

                          DICK      0.8571429           0.000000

                         HARRY       0.000000           1.611429

 

                           Row    Slack or Surplus      Dual Price

                             1        10.57143           1.000000

                             2       0.000000           1.257143

                             3        0.000000           4.285714

 

变量TOM、DICK的取值没有变化分别为2.000000、0.8571429.从变量HARRY的Reduced Cost中看到从原来得3.611429到现在得1.611429差为2.如果如果系数变化在Reduced Cost内,优化取值不变.

 

Slack or Surplus（小于：松弛，大于：过剩）：

如果满足约束条件,则该值是左右差的绝对值.

如果不满足约束条件,则该值为负数.

如果该值为0,说明两边相等.

例2模型如下：

Max = 3 * X + 4 * Y;

           X          <= 40;

                     Y <= 60;

           X +      Y <=80;

解该模型，得到的Solution Report如下：

  Global optimal solution found atiteration:            0

  Objectivevalue:                                300.0000

 

 

                      Variable          Value        Reduced Cost

                             X        20.00000           0.000000

                             Y       60.00000           0.000000

 

                           Row    Slack or Surplus      Dual Price

                             1        300.0000           1.000000

                             2        20.00000           0.000000

                             3       0.000000           1.000000

4       0.000000           3.000000

把X=20.00000，Y=60.00000代入目标函数和约束条件：

1    Max=300;      300

2    20<=40;       20

3    60<=60;       0

4    20+60<=80;    0

 

Dual Price：

如果该行右边数值加1，就得到优化模型相应的加上该行的Dual Price或减去该行的Dual Price。举例如下：

在例2中第4行的Dual Price为3，现在我们在第4行的右边加上1等到如下模型：

Max = 3 * X + 4 * Y;

           X          <= 40;

                     Y <= 60;

           X +      Y <=81;（本来是80）

解该模型，得到的Solution Report如下：

  Global optimal solution found at iteration:            2

  Objectivevalue:                                303.0000

 

 

                      Variable          Value        Reduced Cost

                             X        21.00000           0.000000

                             Y       60.00000           0.000000

 

                           Row    Slack or Surplus      Dual Price

                             1        303.0000           1.000000

                             2        19.00000           0.000000

                             3       0.000000           1.000000

                         4       0.000000           3.000000

Objective value值从300增加到303。

 

2  Range

点击Range命令在当前模型中会产生一个Range report窗口，在该窗口中有两段分别是，Objective Coefficient Ranges（目标函数系数范围）和RighthandSide Ranges（约束条件右边的范围）在例2模型下，产生的range report窗口内容如下：

 

 Ranges in which the basis is unchanged:

 

                                     Objective Coefficient Ranges

                                 Current        Allowable       Allowable

               Variable     Coefficient        Increase         Decrease

                      X        3.000000         1.000000        3.000000

                      Y        4.000000         INFINITY        1.000000

 

                                          Righthand Side Ranges

                    Row         Current        Allowable       Allowable

                                     RHS        Increase         Decrease

                      2        40.00000         INFINITY        20.00000

                      3        60.00000        20.00000         20.00000

                  4        80.00000        20.00000         20.00000

 

Objective Coefficient Ranges：

在Objective Coefficient Ranges中的第一列为目标函数的变量名称，第二列为对应变量名的系数，第三列是系数可增加的最大范围，第四列是系数可减少的最大范围.

改变目标函数的变量系数（在给定的范围内），不改变优化求解中变量的取值.

 

Right-handSide Ranges：

在Right-handSide Ranges中的第一列为row的名称，第二列是常数项或者是右边的值.第三列是该模型的右边最多可以加的量，第四列是该模型的右边最多可以减的量.我们可以回想，在solution report中有DualPrice列，在右边加1（1必须不大于Righthand Side Ranges中，Allowable Increase对应的值），就得到优化模型相应的加上该行的DualPrice或减去该行的Dual Price.

3 Options

该菜单中包含绝大部分的LINGO参数，可设置的tabs内容如下：

·        Interface,

·        GeneralSolver,

·        LinearSolver,

·        NonlinearSolver,

·        IntegerPre-Solver

·        IntegerSolver, and

·        GlobalSolver.

在Interface的tabs面中可以控制LINGO系统的界面（包括是否显示工具栏,界面的大小），输出形式（Terse Output）以及默认的文件格式.其它的tabs内容可以参考帮助文件.

4 Model Statistics

统计该模型的信息，包括行数、变量数、约束条件数等等；在如下模型中：

model:

max=2* x1+3*x2;

x1+2*x2+x3=8;

4*x1+x4=16;

4*x2+x5=12;

end

执行LINGO|ModelStatistics后得到如下：

 Rows=      4 Vars=       2 No. integervars=      0  ( all are linear)

 Nonzeros=       9 Constraint nonz=       4(        1 are +- 1) Density= 0

 Smallestand largest elements in abs value=   1.00000        16.0000

 No.< :       3 No.=:       0 No. >:       0, Obj= MAX, GUBs<=       2

 Singlecols=    0

其中Single cols表示松弛变量；现在我们在上面模型中添加三个松弛变量，模型变为：

model:

max=2*x1+3*x2+0*x3+0*x4+0*x5;

x1+2*x2+x3=8;

4*x1+x4=16;

4*x2+x5=12;

end

执行LINGO|ModelStatistics后得到如下：

Rows=      4 Vars=       5 No. integervars=      0  ( all are linear)

Nonzeros=      12 Constraint nonz=       7(        4 are +- 1) Density= 0

Smallest andlargest elements in abs value=   1.00000        16.0000

No. <:       0 No.=:       3 No. > :      0, Obj= MAX, GUBs <=       2

Singlecols=    3

Single cols由原来的0变到3.

转自：http://blog.csdn.net/q_l_s/article/details/10018539