欧拉筛和埃氏筛(超详细分析筛选过程,差异,证明,时间比较)
分析之前我们先看一下埃氏筛和欧拉筛的代码:
1.Eraosthenes(埃拉托斯尼筛法)埃氏筛法
时间复杂度O(nlogn)
const int maxn=2e6+6;
bool isprime[maxn];
void seive(){
memset(isprime,true,sizeof(isprime));
isprime[0]=isprime[1]=false;
for(int i=2;i<=maxn-6;i++){
if (isprime[i]) {
for (int j = i * i; j <= maxn-6; j += i) {
isprime[j] = false;
}
}
}
}2.欧拉筛法
时间复杂度O(n)
const int N = 1e8 + 3;
bool isprime[N];
int prime[N],cnt;
void ola(int n) {
memset(isprime, true, sizeof(isprime));
isprime[1] = 0;
for (int i = 2; i <= n; i++) {
if (isprime[i]) prime[++cnt] = i;//如果i没有被前面的数筛掉,则i是素数
for (int j = 1; j<=cnt&&prime[j] <= n/i; j++) {//j枚举已经筛出的素数,该循环起到筛掉枚举素数的倍数的作用
isprime[i * prime[j]] = 0;//把i*prime[j]筛掉
if (i % prime[j] == 0) break;//保证不会重复筛
}
}
}
详细筛选过程:
埃氏筛:
假如要筛选素数的范围为1~20000
用isprime[i] 来表示 i 是否为素数
首先把所有的 isprime[] 里面的值都置为true
首先对于0 和 1 设置为false 表示不为质数
用 i 表示从 2 遍历到20000 如果 i 是 素数就进行操作
大体进行流程:
从2开始
将2*2、3*2、4*2、5*2、、、、、、10000*2 所有得到的值
isprime[i] 置为false 表示他们都不是素数
然后从3开始
将2*3、3*3、4*3、5*3、、、、、、6666*3 所有得到的值
isprime[i] 置为false 表示他们都不是素数
然后从4开始(注意这里的4不是素数,故不进行筛选)
然后从5开始
将2*5、3*5、4*5、5*5、、、、、、4000*5 所有得到的值
isprime[i] 置为false 表示他们都不是素数
、、、、、、
最后从20000结束循环(注意这里的20000不是素数,故不进行筛选)
最终我们得到的所有的isprime[i] 里面为true 的即为素数
欧拉筛:
假如要筛选素数的范围为1~20000
用isprime[i] 来表示 i 是否为素数
首先把所有的 isprime[] 里面的值都置为true
首先对于0 和 1 设置为false 表示不为质数
用 i 表示从 2 遍历到20000 如果 i 是 素数就进行操作
(操作:对于每一个 i 乘上已经得到的所有素数,如果遇见了i 可以整除的质数,跳出循环,对于i+1进行操作)
大体进行流程:
从2开始
将2*2得到的值
isprime[i] 置为false 表示他都不是素数
从3开始
将2*3、3*3得到的值
isprime[i] 置为false 表示他都不是素数
从4开始
将2*4得到的值(注意这里对于3*4没有进行筛选,因为4可以整除2,那么就不需要筛后面的数)
isprime[i] 置为false 表示他都不是素数
从5开始
将2*5、3*5、5*5得到的值
isprime[i] 置为false 表示他都不是素数
、、、、、、
从20000结束循环(因为2*20000大于我们要找的范围,故直接退出)
最终我们得到的所有的isprime[i] 里面为true 的即为素数
为什么欧拉筛会比埃氏筛更快:
对于埃氏筛:
大家很容易就可以发现在筛的过程中例如对于6就有重复的筛选。而这一些重复的筛选就使我们筛选的过程中出现的时间的浪费。
对于欧拉筛:
欧拉筛效率高的原因:不重复筛选
欧拉筛特点:合数都是被它的最小素因子筛去的
由上面两点我们就可以得到欧拉筛在筛的时候,将埃氏筛重复筛的过程跳过了,这样就使欧拉筛的时间消耗更小。
筛法做法正确简单证明:
埃氏筛:
例如对于 i=11 ,我们循环 i 到 11 的时候可以直接判断它为素数
原因:
前面所有比11 小的质数 例如2 、3、5、7 都已经把
他们能乘出来的所有合数都筛掉了
那么我们遍历到11的时候就可以直接判断它是否是合数了
欧拉筛:
欧拉筛是从1~20000遍历一遍
然后每一次遍历的时候和所有已经筛出来的素数相乘
虽然和埃氏筛的筛法不一样
但从总体来看我们可以发现筛选的数和埃氏筛差不多
只是去掉了重复的部分:(对于合数能够整除质数的退出操作保证了不会对重复数据进行筛选)
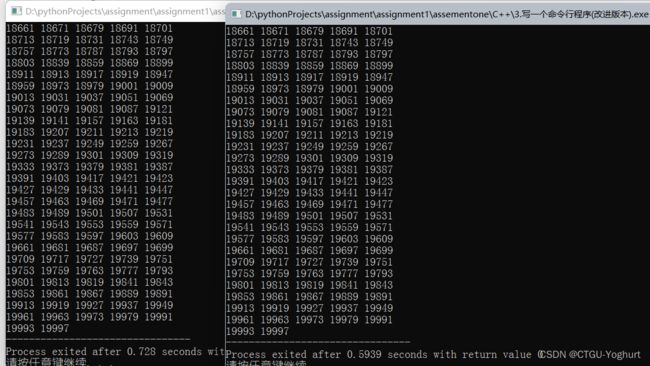
Devc++ 1~20000筛选时间比较:(左为埃氏筛,右为欧拉筛)
埃氏筛代码:
#include
#include
#include
using namespace std;
const int maxn=2e6+6;
const int N=20000;
bool isprime[maxn];
void seive(){
memset(isprime,true,sizeof(isprime));
isprime[0]=isprime[1]=false;
for(int i=2;i<=N;i++){
if (isprime[i]) {
for (int j = i * i; j <= N; j += i) {
isprime[j] = false;
}
}
}
}
int main(){
seive();
int sum=0;
for(int i=1;i<=20000;i++){
if(isprime[i]){
sum++;
if(sum%5==0){
printf("%d\n",i);
}else{
printf("%d ",i);
}
}
}
return 0;
} 欧拉筛:
#include
#include
#include
using namespace std;
const int maxn=2e6+6;
const int N=20000;
bool isprime[maxn];
int prime[N];
int cnt;
void ola(int n) {
memset(isprime, true, sizeof(isprime));
isprime[1] = 0;
for (int i = 2; i <= n; i++) {
if (isprime[i]) prime[++cnt] = i;//如果i没有被前面的数筛掉,则i是素数
for (int j = 1; j<=cnt&&prime[j] <= n/i; j++) {//j枚举已经筛出的素数,该循环起到筛掉枚举素数的倍数的作用
isprime[i * prime[j]] = 0;//把i*prime[j]筛掉
if (i % prime[j] == 0) break;//保证不会重复筛
}
}
}
int main(){
ola(20000);
int sum=0;
for(int i=1;i<=cnt;i++){
if(i%5!=0)
cout<