双目散斑结构光
双目散斑结构光介绍
- 1、什么是散斑结构光
- 2、为什么要用散斑结构光
- 3、如何生成散斑图
- 4、计算机模拟生成散斑图
-
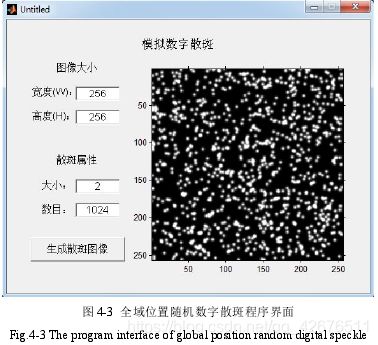
- 4.1 全域位置随机散斑
- 4.2 局域位置随机散斑
- 参考
1、什么是散斑结构光
散斑,也叫伪随机散斑,由一些白色斑点组成的一种结构光图案,是一种空间编码结构光,现在通常与双目立体匹配结合使用,增加纹理信息,改善弱纹理、重复纹理区域的视差效果。
2、为什么要用散斑结构光
结构光有很多种,就会问为什么要用散斑?
那我们先来重温一下结构光的分类,结构光总共分为时间结构光和空间结构光两种。时间结构光按照时间序列对每个像素生成一个唯一的编码值,无法做到实时。那么空间结构光中,也有很多种,可以用方波、正弦波、DeBrujin序列、二维随机点阵(散斑),论文里面给出实验并证明了散斑和DeBrujin序列的双目立体匹配的效果是更好的。

前两列是经过极线校正的散斑图,最后一列是平面视差图,可以看到,方波和正弦波的视差图有明显的条纹现象,而DeBrujin序列和散斑则没有,效果更好。
3、如何生成散斑图
生成散斑图有四个方法:
- 激光照射漫反射表面后干涉产生激光散斑图
- 人工喷涂黑白漆形成散斑图
- 利用某些材料表面的自然特征形成自然散斑图
- 用计算机模拟生成数字散斑图
与其他方法相比,用计算机模拟生成的数字散斑图有以下优点:
- 可以控制散斑点的大小、数目、中心位置等特征;
- 可以控制噪声水平。
4、计算机模拟生成散斑图
4.1 全域位置随机散斑
原理:
这是比较常用的数字散斑的方法,它将一定数目的随机分布的高斯光斑叠加。假设图像的背景光强均匀,则图像灰度函数可表示为:
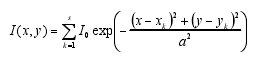
式中,s表示散斑的数目,a表示散斑的尺寸大小, I 0 I_0 I0表示图像背景光强,通常 I 0 I_0 I0为1,一维随机变量 ( x k , y k ) (x_k, y_k) (xk,yk)表示第k个散斑颗粒的中心位置,它可由均匀随机分布函数rand得到,可表示为:
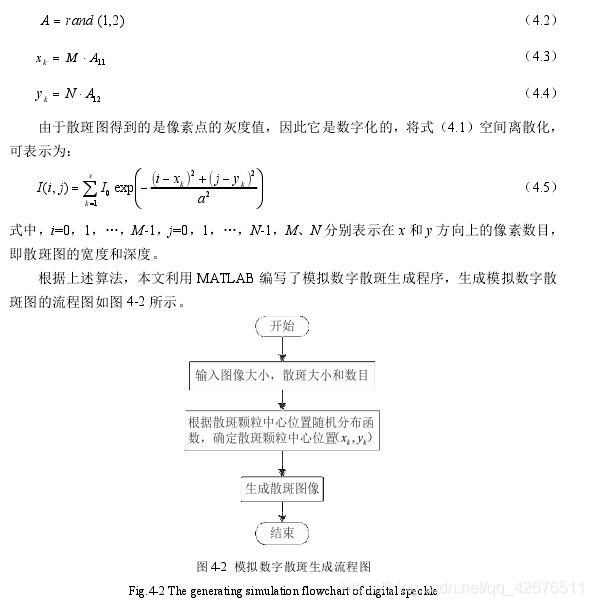
经过实验,全域散斑图的参数有以下设计规则:
- 散斑点要小,即a要小,可设置为1;
- 散斑点要多,即s要大;
- 散斑图要大,即M、N要大。
以上三点规则都是为了避免散斑点的重合,导致大片白色区域出现,影响双目立体匹配的精度。
下面给出全域位置散斑图:
生成散斑图大小为512*512,散斑点半径为1,散斑点数量为4096的散斑图。
clear
clc
Num=4096;
Height=512;
Width=512;
I0=1;
R=1;
xk=randi([1,Height],Num,1);
yk=randi([1,Width],Num,1);
for i=1:1:Height
for j=1:1:Width
Y=I0*exp(-(((i-xk).^2+(j-yk).^2)/R^2));
I(i,j)=sum(Y);
end
end
figure(1);
imshow(I);
imwrite(I,'C:\Users\19728\Desktop\ImgSpeck.bmp');
4.2 局域位置随机散斑
原理:
由于全域位置随机散斑是在全图随机分布的,因此容易使散斑中心位置重合,散斑图像中会出现大片的白色区域,不均匀,降低立体匹配的准确度,而调解参数也始终存在随机性。所以需要对随机散斑生成算法加以改进,给出局域位置随机数字散斑的算法。


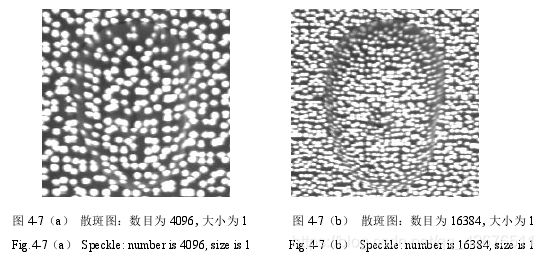
经过实验,小区域要尽量小,但不能小于3,这样生成的散斑点的数量就会更多,能够覆盖更多的区域并且不会重合,即使在深度突变区域也有充足的散斑点,提高深度不连续区域的视差精度。下图是两个不同大小的区域生成的散斑图,可以看到,左边大区域生成的散斑图比较稀疏,在深度不连续区域的散斑点很少,而右图小区域生成的散斑图比较密集。
代码实现:
生成散斑图大小为512*512,散斑点半径为1,散斑点数量为4096的散斑图。
clear
clc
Height=512;
Width=512;
I0=1;
R=1;
m = 8;
n = 8;
p = uint32(Height / m);
q = uint32(Width / n);
xk = zeros([p*q,1]);
yk = zeros([p*q,1]);
for i = 1:1:p
for j = 1:1:q
x1 = randi([1,m]);
y1 = randi([1,n]);
xk((i-1)*q+j,1) = x1 + (i - 1) * m;
yk((i-1)*q+j,1) = y1 + (j - 1) * n;
end
end
for i=1:1:Height
for j=1:1:Width
Y=I0*exp(-(((i-xk).^2+(j-yk).^2)/R^2));
I(i,j) = sum(Y);
end
end
figure(1);
imshow(I);
imwrite(I,'C:\Users\19728\Desktop\ImgSpeck1.bmp');
实验结果:


可以明显的看到,局域位置散斑分布更加均匀,散斑中心不会出现重合的现象,这样能大大的提高匹配的准确率。
参考
[1]王茜. 基于数字散斑的双目视觉三维重建方法研究[D].西安理工大学,2015.
[2]周亭亭. 基于结构光的双目电子内窥镜的三维测量技术[D].浙江大学,2017.