神经网络训练技巧
文章目录
- 一、问题描述
- 二、 设计简要描述
- 三、程序清单
- 四、结果分析
- 五、调试报告
- 六、实验小结
一、问题描述
基于二元函数f(x,y)=z=1/20 x2+y2掌握梯度下降和权重初始化的技巧，基于手写体识别掌握正规化和两种防止过拟合的技巧。
二、 设计简要描述
- 梯度下降方法
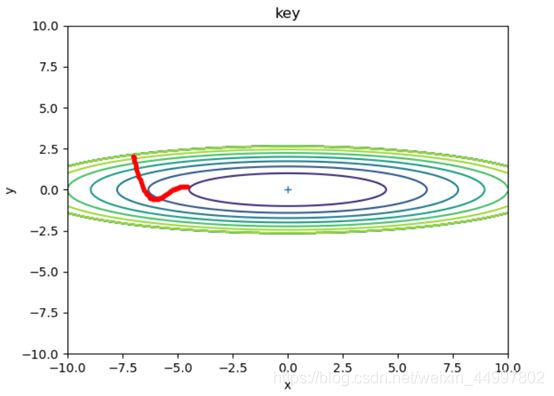
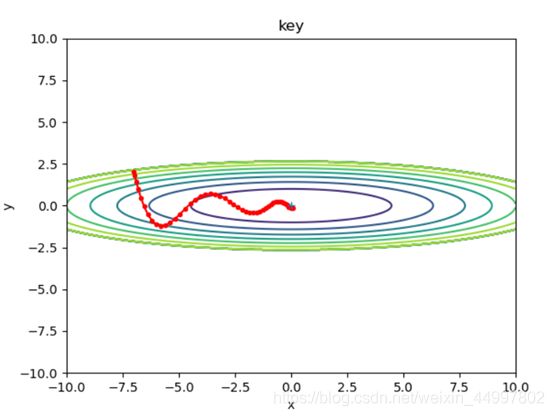
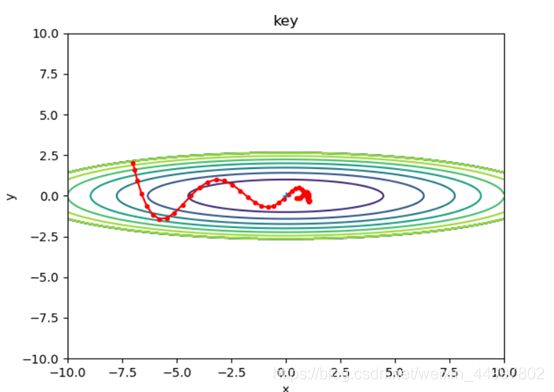
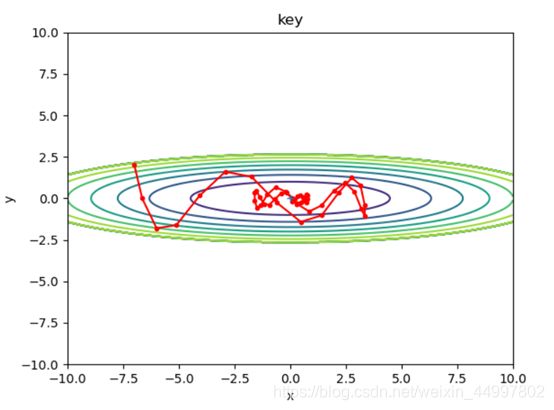
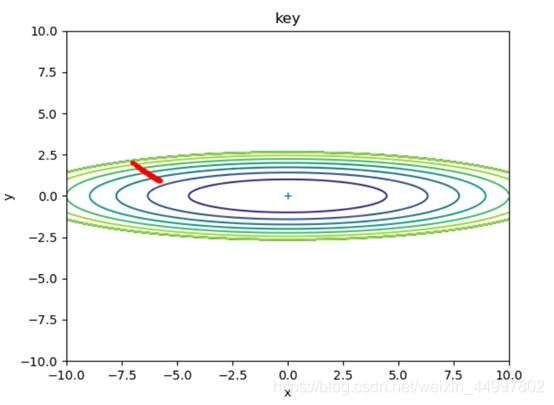
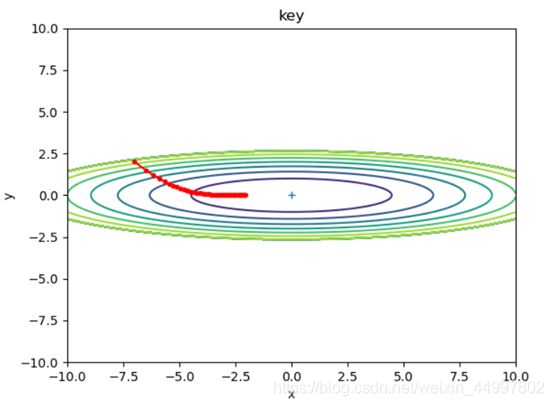
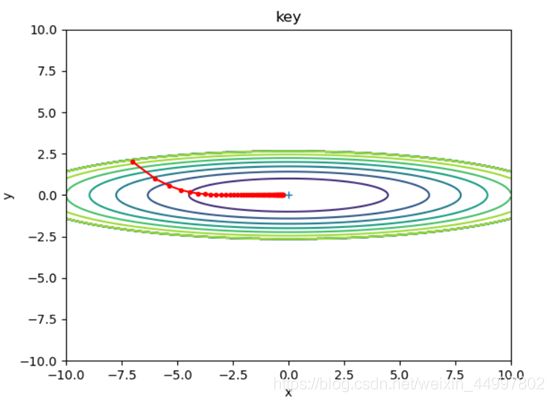
1.1.1 对于SGD模型，固定初始坐标，确定学习率为0.2，改变梯度下降的次数
需要改动的代码 for i in range(50):
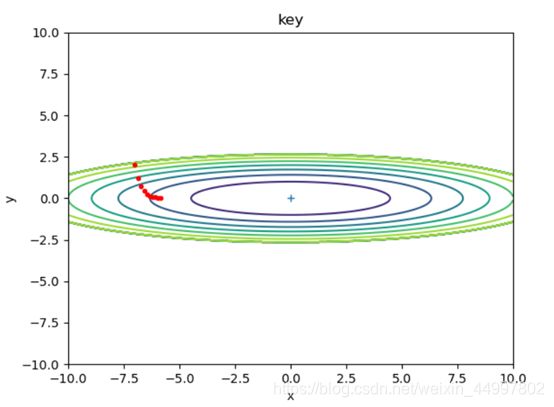
图1
图2
图3
图4
图5
1.1.2 对于SGD模型，固定初始坐标，确定梯度下降次数为50，改变学习率
需要改动的代码 optimizer = SGD(lr=0.7)
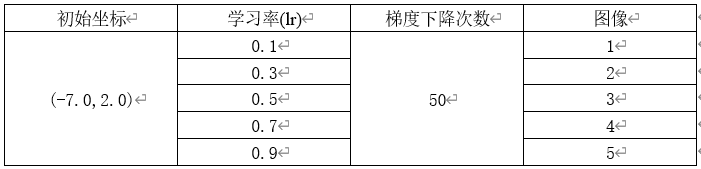
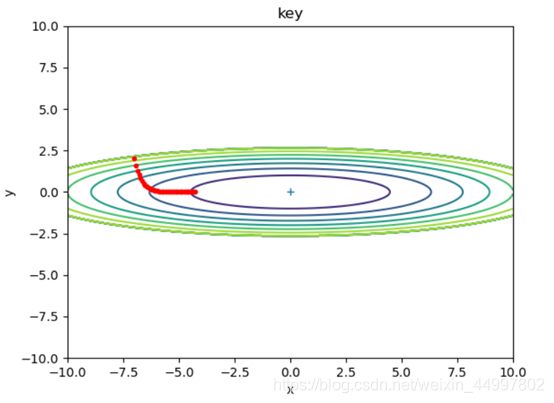
图1
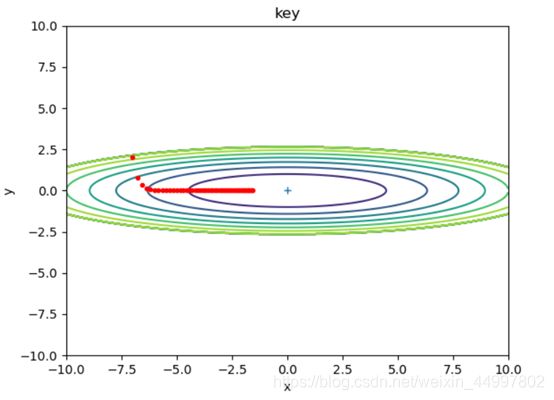
图2
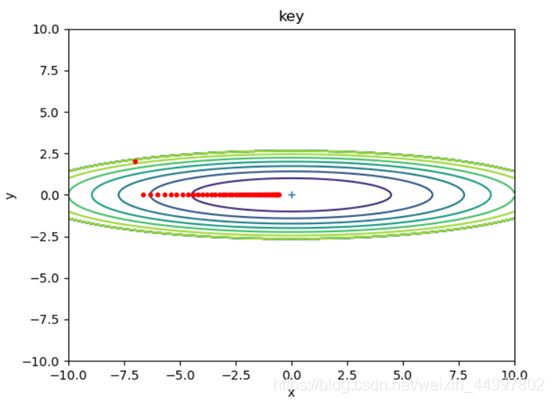
图3
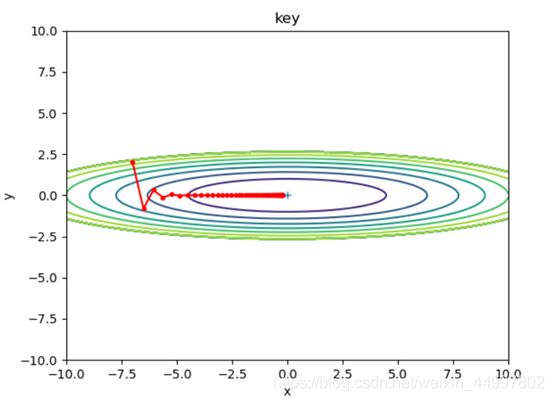
图4
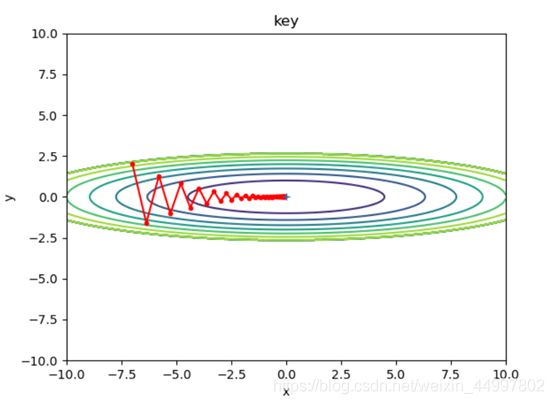
图5
1.2 对于Momentum模型，固定初始坐标，确定动量momentum为0.9，改变学习率
需要改变的代码 optimizer = Momentum(lr=0.5,momentum=0.9)
初始坐标 学习率(lr) 动量(momentum) 图像
图1
图2
图3
图4
1.3 对于AdaGrad模型，固定初始坐标，改变学习率
需要改变的代码行 optimizer = AdaGrad(lr=0.5)
图1
图2
图3
- 初始化权重
2.1 五层网络初始权重是标准差为1的高斯分布，其每一层的激活值分布情况
关键代码 w = np.random.randn(node_num, node_num) * 1
2.2 五层网络初始权重是标准差为0.01的高斯分布，其每一层的激活值分布情况
关键代码 w = np.random.randn(node_num, node_num) * 0.01
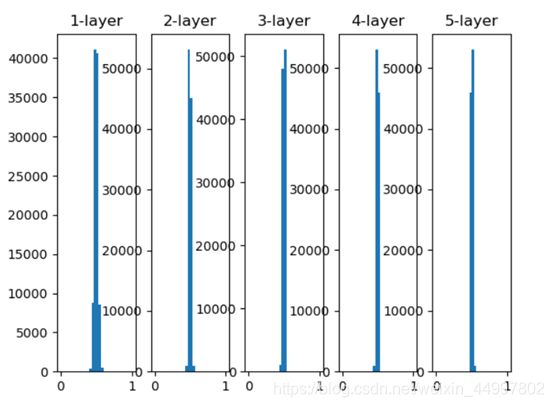
2.3 五层网络初始权重值为Xavier初始值，其每一层的激活值分布情况
关键代码 w = np.random.randn(node_num, node_num) / np.sqrt(node_num)
2.4 五层网络初始权重值为He初始值，其每一层的激活值分布情况
关键代码 w = np.random.randn(node_num, node_num) / np.sqrt(node_num/2)
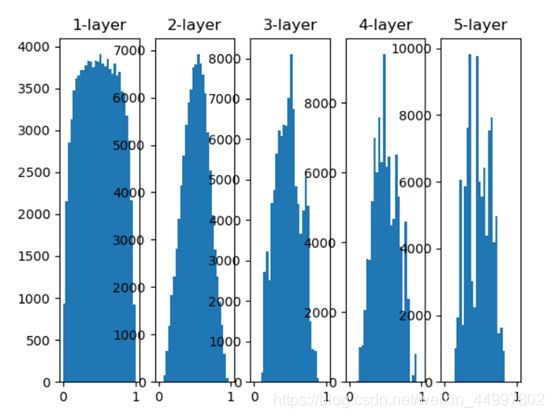
3.正则化
3.1 不使用batch norm层
3.2 使用batch norm层
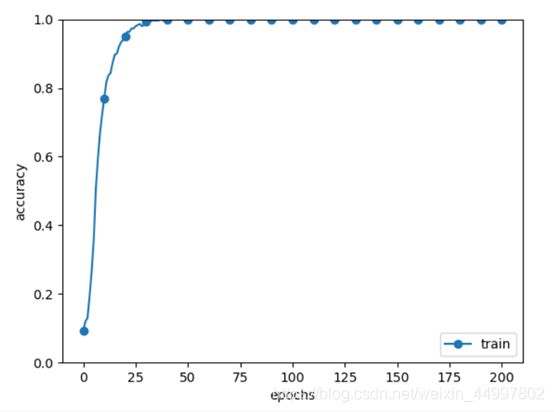
图1
图2
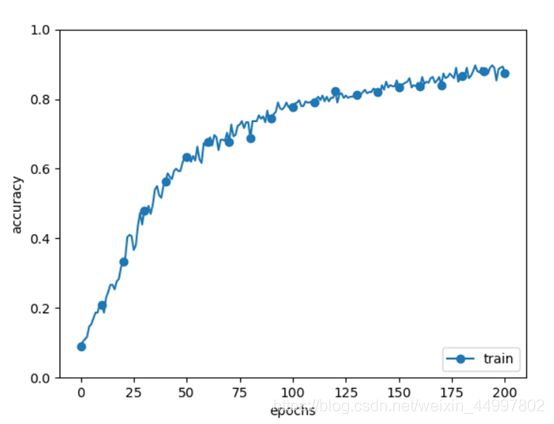
图3
图4
4.正则化
4.1 过拟合的结果，无权重衰减，无dropout
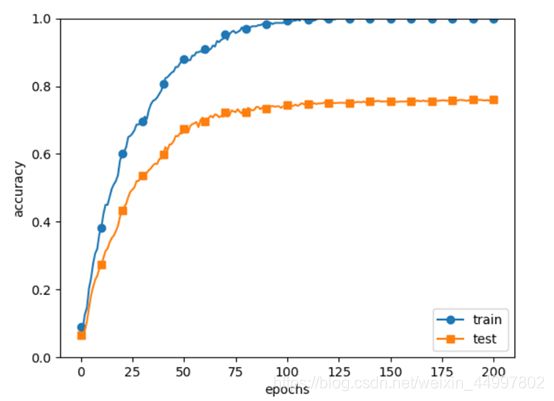
4.2 有权重衰减，无dropout
主要修改代码行
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0.1):
# 使用权重衰减
self.weight_decay_lambda = weight_decay_lambda
在损失函数中添加
# 使用权重衰减
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.last_layer.forward(y, t) + weight_decay
gradient函数修改
for idx in range(1, self.hidden_layer_num + 2):
grads['W' + str(idx)] = self.layers['Linear' + str(idx)].dW + self.weight_decay_lambda * self.params[
'W' + str(idx)]
grads['b' + str(idx)] = self.layers['Linear' + str(idx)].db
4.3 无权重衰减，有dropout
主要修改代码行
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0,use_dropout=True, dropout_ration=0.2):
#添加dropout层
self.use_dropout = use_dropout
在定义生成层时添加
if self.use_dropout:
self.layers['Dropout' + str(idx)] = Dropout(dropout_ration)
三、程序清单
AdaGrad.py
import numpy as np
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def step(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
Momentum.py
import numpy as np
class Momentum:
"""Momentum SGD"""
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def step(self, params, grads):
# 初始化速度v
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
MultiLayerNet2.py是修改后的网络层代码，综合了三四两部分
import numpy as np
class BatchNormalization:
def __init__(self, gamma, beta, momentum=0.3, running_mean=None, running_var=None):
self.gamma = gamma
self.beta = beta
self.momentum = momentum
self.input_shape = None # Conv层的情况下为4维，全连接层的情况下为2维
# 测试时使用的平均值和方差
self.running_mean = running_mean
self.running_var = running_var
# backward时使用的中间数据
self.batch_size = None
self.xc = None
self.std = None
self.dgamma = None
self.dbeta = None
def forward(self, x, train_flg=True):
self.input_shape = x.shape
#将每一个样本由三维数组转换为一维数组
if x.ndim != 2:
N, C, H, W = x.shape
x = x.reshape(N, -1)
#在__forward方法中完成BatchNorm函数的前向传播
out = self.__forward(x, train_flg)
return out.reshape(*self.input_shape)
def __forward(self, x, train_flg):
if self.running_mean is None:
N, D = x.shape
self.running_mean = np.zeros(D)
self.running_var = np.zeros(D)
if train_flg:
mu = x.mean(axis=0)
xc = x - mu
var = np.mean(xc**2, axis=0)
std = np.sqrt(var + 10e-7)
xn = xc / std
self.batch_size = x.shape[0]
self.xc = xc
self.xn = xn
self.std = std
self.running_mean = self.momentum * self.running_mean + (1 - self.momentum) * mu
self.running_var = self.momentum * self.running_var + (1 - self.momentum) * var
else:
xc = x - self.running_mean
xn = xc / ((np.sqrt(self.running_var + 10e-7)))
out = self.gamma * xn + self.beta
return out
def backward(self, dout):
if dout.ndim != 2:
N, C, H, W = dout.shape
dout = dout.reshape(N, -1)
dx = self.__backward(dout)
dx = dx.reshape(*self.input_shape)
return dx
def __backward(self, dout):
dbeta = dout.sum(axis=0)
dgamma = np.sum(self.xn * dout, axis=0)
dxn = self.gamma * dout
dxc = dxn / self.std
dstd = -np.sum((dxn * self.xc) / (self.std * self.std), axis=0)
dvar = 0.5 * dstd / self.std
dxc += (2.0 / self.batch_size) * self.xc * dvar
dmu = np.sum(dxc, axis=0)
dx = dxc - dmu / self.batch_size
self.dgamma = dgamma
self.dbeta = dbeta
return dx
四、结果分析
-
梯度下降方法
结论一：SGD模型，当学习率固定，梯度下降的次数过少时，f(x,y)无法到达最小值
结论二：SGD模型，当梯度下降的次数固定，增大学习率，每次改变的位置跨度越大。学习率过小时，可能无法到达最低点。
结论三：Momentum确实能够加速收敛、减小震荡，但是要注意设置较小的学习率。
结论四：AdaGrad由于其自身不断减小学习率的特性，可以在最初把学习率设置为一个较大的值。 -
初始化权重
结论：为了解决梯度消失问题，本次实验提供了3中有效的解决方案：
①仍采用高斯分布，但将权重的标准差设为0.01
②使用Xavier权重初始值
③使用He权重初始值
从实验结果可以看出，如果认为各层的激活值越集中于0.5，越不容易发生梯度消失，那么三者的有效性是依次递减的。 -
正则化
结论：对比实验结果可以看出正则化作为有效的加速学习的方法，在momentum值设置为0.9时可以达到加速效果，在0.9以下则不能。 -
防止过拟合
结论：从实验结果可以看出，使用权重衰减的方法和添加dropout层都不失为防止过拟合的好方法，但运行添加了dropout层的程序明显慢很多，且从结果上来看也降低了学习速度。
五、调试报告
-
控制台报错
Traceback (most recent call last):
File “E:/project/pythonProject/07_trainingSkills/Function.py”, line 23, in
optimizer = Momentum(lr=0.01, momentum=0.9)
TypeError: ‘module’ object is not callable
原因：导包的方式不对
解决：将import Momentum改成from Momentum import Momentum -
运行Adam模型时控制台报错
Traceback (most recent call last):
File “E:/project/pythonProject/07_trainingSkills/Function.py”, line 44, in
optimizer.step(params, grads)
File “E:\project\pythonProject\07_trainingSkills\Adam.py”, line 26, in step
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
KeyError: ‘y’
原因：没有’y’这个键 -
学会使用numpy.random.randn(d0, d1, …, dn)函数构建不同数学期望μ和方差σ^2的正态分布
-
学会使用subplot函数确定子图表的位置
前两个参数把空间分成其乘积块数
第三个参数不可以大于前两个参数的乘积
-
控制台报错
ImportError: cannot import name ‘MultiLayerNet’ from partially initialized module ‘MultiLayerNet’ (most likely due to a circular import)
解决：将所有类移到同一级目录下 -
控制台报错
Compressed file ended before the end-of-stream marker was reached
原因：数据包导到一半停止了
解决：用之前实验下载好的数据包将其覆盖 -
控制台报错
TypeError: forward() takes 2 positional arguments but 3 were given
原因：实际上是全连接层求反向传播只要一个参数而传入了两个
解决：最后一层还是用SoftmaxWithLoss层 -
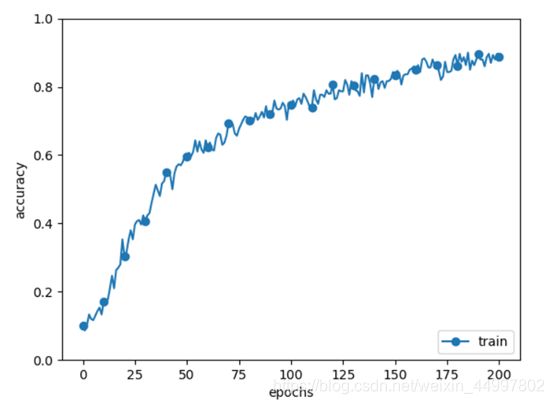
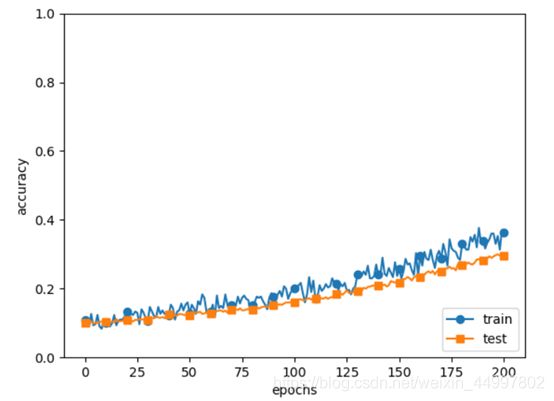
模拟过拟合的部分，写好网络类后第一次运行结果是这样的
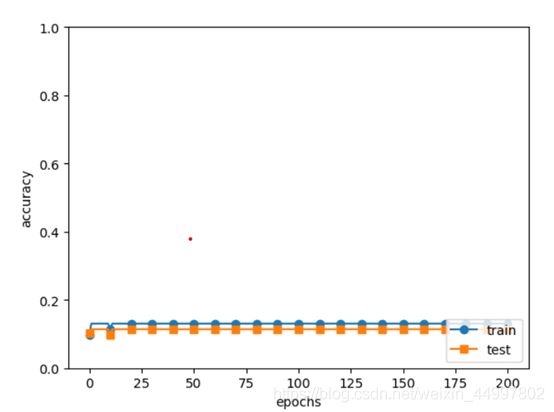
分析：编码方式有问题
解决：中途因为控制台报错改成了独热编码，但实际应该为
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True) -
加入了dropout层并设置dropout_ration=0.2后学习效率并不如指导书上一样高，而是
分析：忘记修改predict函数
解决：predict函数修改前后分别为
前
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
后
def predict(self, x, train_flg=False):
for key, layer in self.layers.items():
if "Dropout" in key or "BatchNorm" in key:
x = layer.forward(x, train_flg)
else:
x = layer.forward(x)
return x
修改后的实验结果为
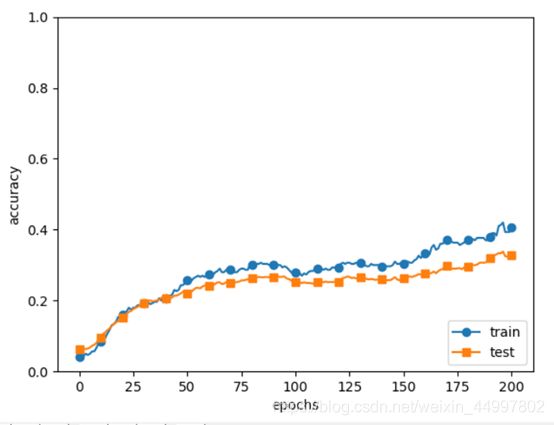
学习效率仍是很低，再分析指导书上的应该是同时用上了batch norm和dropout
于是将参数use_dropout设置为True
六、实验小结
本次实验在实验五六的基础上，通过对比实验的方式，学习了几种不同的梯度下降方式，初始化权重方式，加速网络学习的方式以及防止过拟合的方式。遇到的困难主要是第四部分防止过拟合的网络构建。