循环神经网络--01 序列模型
生成数据
import torch
from torch import nn
from d2l import torch as d2l
T = 1000
time = torch.arange(1,T+1,dtype=torch.float32)
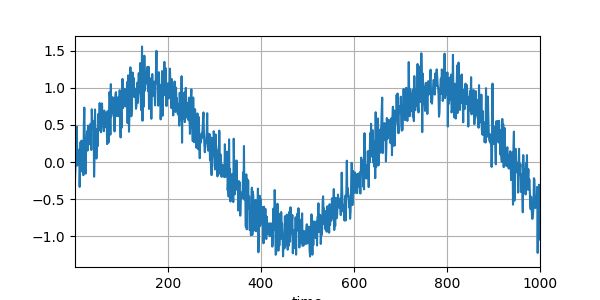
x = torch.sin(0.01*time)+torch.normal(0,0.2,(T,))
d2l.plot(time,x,'time',xlim=[1,1000],figsize=(6,3))
将序列转换为特征-标签对(feature-label)
tau = 4
features = torch.zeros((T - tau,tau)) # 初始化特征矩阵
for i in range(tau):
features[:,i] = x[i:T-tau+i]
labels = x[tau:].reshape(-1,1)
batch_size ,n_train = 16,600
train_iter = d2l.load_array((features[:n_train],labels[:n_train]),batch_size,is_train=True)
构建模型
一个简单的多层感知机
一个拥有两个全连接层的多层感知机,ReLU激活函数和平方损失。
def init_weights(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weights)
# 一个简单的多层感知机
def get_net():
"""一个拥有两个全连接层的多层感知机,ReLU激活函数和平方损失 """
net = nn.Sequential(nn.Linear(4,10),
nn.ReLU(),
nn.Linear(10,1))
net.apply(init_weights)
return net
loss = nn.MSELoss(reduction='none')
训练模型
训练模型
def train(net,train_iter,loss,epochs,lr):
# 目标优化函数 和 学习率
trainer = torch.optim.Adam(net.parameters(),lr)
for epoch in range(epochs):
for X,y in train_iter:
trainer.zero_grad()
l = loss(net(X),y)
l.sum().backward()
trainer.step()
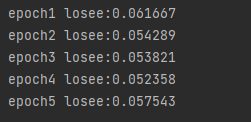
print(f'epoch{epoch+1}',f'losee:{d2l.evaluate_loss(net,train_iter,loss):f}')
net = get_net()
train(net,train_iter,loss,5,0.01)
预测
单步预测
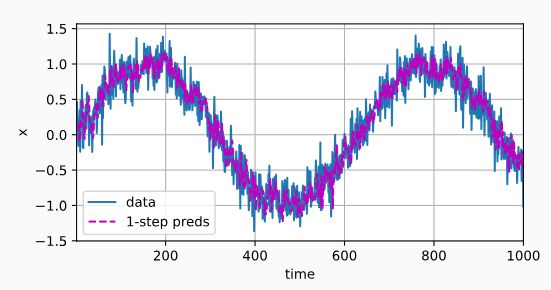
onestep_preds = net(features)
d2l.plot([time,time[tau:]],[x.detach().numpy(),onestep_preds.detach().numpy()],'time','x',legend=['data','1-step preds'],xlim=[1,1000],figsize=(6,3))
多步预测
## 多步预测
multistep_preds = torch.zeros(T)
multistep_preds[:n_train+tau] = x[:n_train+tau]
for i in range(n_train+tau,T):
multistep_preds[i] = net(multistep_preds[i-tau:i].reshape(1,-1))
d2l.plot([time, time[tau:], time[n_train + tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy(),
multistep_preds[n_train + tau:].detach().numpy()], 'time',
'x', legend=['data', '1-step preds', 'multistep preds'],
xlim=[1, 1000], figsize=(6, 3))


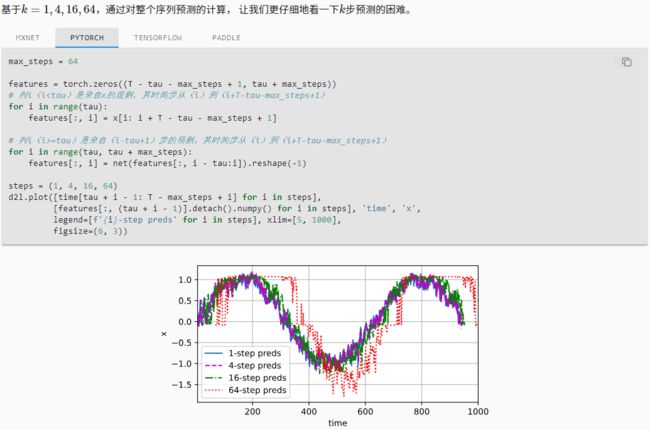
以上例子清楚地说明了当我们试图预测更远的未来时,预测的质量是如何变化的。 虽然“4-
步预测”看起来仍然不错,但超过这个跨度的任何预测几乎都是无用的。
全部代码
import torch
from torch import nn
from d2l import torch as d2l
# 生成序列数据
T = 1000
time = torch.arange(1,T+1,dtype=torch.float32)
x = torch.sin(0.01*time)+torch.normal(0,0.2,(T,))
d2l.plot(time,x,'time',xlim=[1,1000],figsize=(6,3))
#将序列转换为模型的特征-标签对
tau = 4
features = torch.zeros((T - tau,tau)) # 初始化特征矩阵
for i in range(tau):
features[:,i] = x[i:T-tau+i]
labels = x[tau:].reshape(-1,1)
batch_size ,n_train = 16,600
train_iter = d2l.load_array((features[:n_train],labels[:n_train]),batch_size,is_train=True)
# 构建模型
# 一个简单的多层感知机
#"""一个拥有两个全连接层的多层感知机,ReLU激活函数和平方损失。"""
def init_weights(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
def get_net():
"""一个拥有两个全连接层的多层感知机,ReLU激活函数和平方损失 """
net = nn.Sequential(nn.Linear(4,10),
nn.ReLU(),
nn.Linear(10,1))
net.apply(init_weights)
return net
loss = nn.MSELoss(reduction='none')
# 训练模型
def train(net,train_iter,loss,epochs,lr):
# 目标优化函数 和 学习率
trainer = torch.optim.Adam(net.parameters(),lr)
for epoch in range(epochs):
for X,y in train_iter:
trainer.zero_grad()
l = loss(net(X),y)
l.sum().backward()
trainer.step()
print(f'epoch{epoch+1}',f'losee:{d2l.evaluate_loss(net,train_iter,loss):f}')
net = get_net()
train(net,train_iter,loss,5,0.01)
# 预测
# 单步预测
onestep_preds = net(features)
d2l.plot([time,time[tau:]],[x.detach().numpy(),onestep_preds.detach().numpy()],'time','x',legend=['data','1-step preds'],xlim=[1,1000],figsize=(6,3))
## 多步预测
multistep_preds = torch.zeros(T)
multistep_preds[:n_train+tau] = x[:n_train+tau]
for i in range(n_train+tau,T):
multistep_preds[i] = net(multistep_preds[i-tau:i].reshape(1,-1))
d2l.plot([time, time[tau:], time[n_train + tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy(),
multistep_preds[n_train + tau:].detach().numpy()], 'time',
'x', legend=['data', '1-step preds', 'multistep preds'],
xlim=[1, 1000], figsize=(6, 3))